Chapter 4 Numerical Linear Algebra
4.1 Preliminaries
Much of this material is based on
G. H. Golub and C. F. VanLoan (2013), Matrix Computations, 4th Ed., JHU Press.
4.1.1 Conditioning and Stability
Some problems are inherently difficult: no algorithm involving rounding of inputs can be expected to work well. Such problems are called ill-conditioned.
A numerical measure of conditioning, called a condition number, can sometimes be defined:
Suppose the objective is to compute \(y = f(x)\).
If \(x\) is perturbed by \(\Delta x\) then the result is changed by
\[\Delta y = f(x + \Delta x) - f(x).\]
If
\[\frac{|\Delta y|}{|y|} \approx \kappa \frac{|\Delta x|}{|x|}\]
for small perturbations \(\Delta x\) then \(\kappa\) is the condition number for the problem of computing \(f(x)\).
A particular algorithm for computing an approximation \(\tilde{f}(x)\) to \(f(x)\) is numerically stable if for small perturbations \(\Delta x\) of the input the result is close to \(f(x)\).
4.1.2 Error Analysis
Analyzing how errors accumulate and propagate through a computation, called forward error analysis, is sometimes possible but often very difficult.
Backward error analysis tries to show that the computed result
\[\begin{equation*} \tilde{y} = \tilde{f}(x) \end{equation*}\]
is the exact solution to a slightly perturbed problem, i.e.
\[\begin{equation*} \tilde{y} = f(\tilde{x}) \end{equation*}\] for some \(\tilde{x} \approx x\).
If
the problem of computing \(f(x)\) is well conditioned, and
the algorithm \(\tilde{f}\) is stable,
then
\[\begin{align*} \tilde{y} &= \tilde{f}(x) & \text{computed result}\\ & = f(\tilde{x}) & \text{exact result for some $\tilde{x} \approx x$}\\ &\approx f(x) & \text{since $f$ is well-conditioned} \end{align*}\]
Backward error analysis is used heavily in numerical linear algebra.
4.2 Solving Linear Systems
Many problems involve solving linear systems of the form
\[\begin{equation*} A x = b \end{equation*}\]
least squares normal equations:
\[X^TX \beta = X^T y\]
stationary distribution of a Markov chain:
\[\begin{align*} \pi P &= \pi\\ \sum \pi_i &= 1 \end{align*}\]
If \(A\) is \(n \times n\) and non-singular then in principle the solution is
\[\begin{equation*} x = A^{-1} b \end{equation*}\]
This is not usually a good numerical approach because
- it can be numerically inaccurate;
- it is inefficient except for very small \(n\).
4.2.1 Triangular Systems
Triangular systems are easy to solve.
The upper triangular system
\[\begin{equation*} \begin{bmatrix} 5 & 3 \\ 0 & 2 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 16\\ 4 \end{bmatrix} \end{equation*}\]
has solution
\[\begin{align*} x_2 & = 4 / 2 = 2\\ x_1 &= (16 - 3 x_2)/5 = 10/5 = 2 \end{align*}\]
This is called back substitution
Lower triangular systems are solved by forward substitution.
If one of the diagonal elements in a triangular matrix is zero, then the matrix is singular.
If one of the diagonal elements in a triangular matrix is close to zero, then the solution is very sensitive to other inputs:
\[\begin{equation*} \begin{bmatrix} 1 & a \\ 0 & \epsilon \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} b_1\\ b_2 \end{bmatrix} \end{equation*}\]
has solution
\[\begin{align*} x_2 & = \frac{b_2}{\epsilon}\\ x_1 &= b_1 - a \frac{b_2}{\epsilon} \end{align*}\]
This sensitivity for small \(\epsilon\) is inherent in the problem: For small values of \(\epsilon\) the problem of finding the solution \(x\) is ill-conditioned.
4.2.2 Gaussian Elimination
The system
\[\begin{equation*} \begin{bmatrix} 5 & 3 \\ 10 & 8 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 16\\ 36 \end{bmatrix} \end{equation*}\]
can be reduced to triangular form by subtracting two times the first equation from the second.
In matrix form:
\[\begin{equation*} \begin{bmatrix} 1 & 0\\ -2 & 1 \end{bmatrix} \begin{bmatrix} 5 & 3 \\ 10 & 8 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 1 & 0\\ -2 & 1 \end{bmatrix} \begin{bmatrix} 16\\ 36 \end{bmatrix} \end{equation*}\]
or
\[\begin{equation*} \begin{bmatrix} 5 & 3 \\ 0 & 2 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 16\\ 4 \end{bmatrix} \end{equation*}\]
which is the previous triangular system.
For a general \(2 \times 2\) matrix \(A\) the lower triangular matrix used for the reduction is
\[\begin{equation*} \begin{bmatrix} 1 & 0\\ -\frac{a_{21}}{a_{11}} & 1 \end{bmatrix} \end{equation*}\]
The ratio \(\frac{a_{21}}{a_{11}}\) is a called a multiplier.
This strategy works as long as \(a_{11} \neq 0\).
If \(a_{11} \approx 0\), say
\[\begin{equation*} A = \begin{bmatrix} \epsilon & 1\\ 1 & 1 \end{bmatrix} \end{equation*}\]
for small \(\epsilon\), then the multiplier \(1/\epsilon\) is large and this does not work very well, even though \(A\) is very well behaved.
Using this approach would result in a numerically unstable algorithm for a well-conditioned problem.
4.2.3 Partial Pivoting
We can ensure that the multiplier is less than or equal to one in magnitude by switching rows before eliminating:
\[\begin{equation*} \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 5 & 3 \\ 10 & 8 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 16\\ 36 \end{bmatrix} \end{equation*}\]
or
\[\begin{equation*} \begin{bmatrix} 10 & 8\\ 5 & 3 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 36\\ 16 \end{bmatrix} \end{equation*}\]
The matrix to reduce this system to triangular form is now
\[\begin{equation*} \begin{bmatrix} 1 & 0\\ -0.5 & 1 \end{bmatrix} \end{equation*}\]
So the final triangular system is constructed as
\[\begin{equation*} \begin{bmatrix} 1 & 0\\ -0.5 & 1 \end{bmatrix} \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 5 & 3 \\ 10 & 8 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 1 & 0\\ -0.5 & 1 \end{bmatrix} \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 16\\ 36 \end{bmatrix} \end{equation*}\]
or
\[\begin{equation*} \begin{bmatrix} 10 & 8\\ 0 & -1 \\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 36\\ -2 \end{bmatrix} \end{equation*}\]
Equivalently, we can think of our original system as
\[\begin{equation*} \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0.5 & 1 \end{bmatrix} \begin{bmatrix} 10 & 8\\ 0 & -1 \\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix} 16\\ 36 \end{bmatrix} \end{equation*}\]
The decomposition of \(A\) as
\[\begin{equation*} A = P L U \end{equation*}\]
with \(P\) a permutation matrix, \(L\) lower trianbular with ones on the diagonal, and \(U\) upper triangular is called a PLU decomposition.
4.2.4 PLU Decomposition
In general, we can write a square matrix \(A\) as
\[\begin{equation*} A = P L U \end{equation*}\]
where
\(P\) is a permutation matrix, i.e.
- it is an identity matrix with some rows switched
- it satisfies \(P P^T = P^T P = I\), i.e. it is an orthogonal matrix
\(L\) is a unit lower triangular matrix, i.e.
- it is lower triangular
- it has ones on the diagonal
\(U\) is upper triangular
The permutation matrix \(P\) can be chosen so that the multipliers used in forming \(L\) all have magnitude at most one.
\(A\) is non-singular if and only if the diagonal entries in \(U\) are all non-zero.
If \(A\) is non-singular, then we can solve
\[\begin{equation*} A x = b \end{equation*}\]
or
\[\begin{equation*} PLU x = b. \end{equation*}\]
in three steps:
- Solve \(P z = b\) for \(z = P^Tb\) (permute the right hand side)
- Solve \(L y = z\) for \(y\) (forward solve lower triangular system)
- Solve \(U x = y\) for \(x\) (back solve upper triangular system)
Computational complexity:
Computing the PLU decomposition takes \(O(n^3)\) operations.
Computing a solution from a PLU decomposition takes \(O(n^2)\) operations.
4.2.5 Condition Number
Linear systems \(Ax=b\) have unique solutions if \(A\) is non-singular.
Solutions are sensitive to small perturbations if \(A\) is close to singular.
We need a useful measure of closeness to singularity
The condition number is a useful measure:
\[\begin{align*} \renewcommand{\Norm}[1]{\|{#1}\|} \kappa(A) &= \frac{\max_{x \ne 0} \frac{\Norm{Ax}}{\Norm{x}}} {\min_{x \ne 0} \frac{\Norm{Ax}}{\Norm{x}}} \\ &= \left(\max_{x \ne 0} \frac{\Norm{Ax}}{\Norm{x}}\right) \left(\max_{x \ne 0} \frac{\Norm{A^{-1}x}}{\Norm{x}}\right) \\ &= \Norm{A}\Norm{A^{-1}} \end{align*}\]
where \(\Norm{y}\) is a vector norm (i.e. a measure of length) of \(y\) and
\[ \Norm{B} = \max_{x \ne 0} \frac{\Norm{Bx}}{\Norm{x}} \]
is the corresponding matrix norm of \(B\).
Some common vector norms:
\[\begin{align*} \|x\|_2 &= \sqrt{\sum_{i=1}^n x_i^2} & \text{Euclidean norm}\\ \|x\|_1 &= \sum_{i=1}^n |x_i| & \text{$L_1$ norm, Manhattan norm}\\ \|x\|_\infty &= \max_i |x_i| & \text{$L_\infty$ norm} \end{align*}\]
4.2.6 Some Properties of Condition Numbers
\(\kappa(A) \ge 1\) for all \(A\).
\(\kappa(A) = \infty\) if \(A\) is singular
If \(A\) is diagonal, then
\[\begin{equation*} \kappa(A) = \frac{\max |a_{ii}|}{\min |a_{ii}|} \end{equation*}\]
Different norms produce different values; the values are usually qualitatively similar
4.2.7 Sensitivity of Linear Systems
Suppose \(x\) solves the original system and \(x^{*}\) solves a slightly perturbed system,
\[\begin{equation*} (A + \Delta A) x^{*} = b + \Delta b \end{equation*}\]
and suppose that
\[\begin{align*} \delta \kappa(A) &\le \frac{1}{2}\\ \frac{\Norm{\Delta A}}{\Norm{A}} & \le \delta\\ \frac{\Norm{\Delta b}}{\Norm{b}} & \le \delta \end{align*}\]
Then
\[\begin{equation*} \frac{\Norm{x-x^{*}}}{\Norm{x}} \le 4 \delta \kappa(A) \end{equation*}\]
4.2.8 Stability of Gaussian Elimination with Partial Pivoting
Backward error analysis: The numerical solution \(\hat{x}\) to the system
\[\begin{equation*} Ax = b \end{equation*}\]
produced by Gaussian elimination with partial pivoting is the exact solution for a perturbed system
\[\begin{equation*} (A + \Delta A) \hat{x} = b \end{equation*}\]
with
\[\begin{equation*} \frac{\Norm{\Delta A}_{\infty}}{\Norm{A}_{\infty}} \le 8 n^3 \rho \mathbf{u}+ O(\mathbf{u}^2) \end{equation*}\]
The value of \(\rho\) is not guaranteed to be small, but is rarely larger than 10
The algorithm would be considered numerically stable if \(\rho\) were guaranteed to be bounded.
Complete pivoting is a bit more stable, but much more work.
The algorithm is considered very good for practical purposes.
4.2.9 General Linear Systems in R
R provides
solvefor general systems, based on LAPACK’s DGESV.DGESV uses the \(P L U\) decomposition.
forwardsolve,backsolvefor triangular systems.kappacomputes an estimate of the condition number or the exact condition number based on the Euclidean norm.
4.3 Cholesky Factorization
Suppose \(A\) is symmetric and (strictly) positive definite, i.e.
\[\begin{equation*} x^T A x > 0 \end{equation*}\]
for all \(x \ne 0\). Some examples:
If \(X\) is the \(n \times p\) design matrix for a linear model and \(X\) is of rank \(p\), then \(A = X^T X\) is strictly positive definite.
If \(X\) is not of full rank then \(A = X^T X\) is non-negative definite or positive semi-definite, i.e. \(x^T A x \ge 0\) for all \(x\).
If \(A\) is the covariance matrix of a random vector \(X\) then \(A\) is positive semidefinite: \[\begin{align*} c^T A c &= c^T E[(X-\mu)(X-\mu)^T] c\\ &= E[((X-\mu)^T c)^T (X - \mu)^T c]\\ &= \text{Var}((X - \mu)^T c) \ge 0 \end{align*}\]
The covariance matrix is strictly positive definite unless \(P(c^T X = c^T\mu) = 1\) for some \(c \ne 0\), i.e. unless there is a perfect linear relation between some of the components of \(X\).
Theorem:
If \(A\) is strictly positive definite, then there exists a unique lower triangular matrix \(L\) with positive diagonal entries such that
\[\begin{equation*} A = L L^T \end{equation*}\]
This is called the Cholesky factorization.
4.3.1 Properties of the Cholesky Factorization Algorithm
It uses the symmetry to produce an efficient algorithm.
The algorithm needs to take square roots to find the diagonal entries.
An alternative that avoids square roots factors \(A\) as
\[\begin{equation*} A = L D L^T \end{equation*}\]
with \(D\) diagonal and \(L\) unit lower triangular.
The algorithm is numerically stable, and is guaranteed not to attempt square roots of negative numbers if
\[ q_n \mathbf{u}\kappa_2(A) \le 1 \]
where \(q_n\) is a small constant depending on the dimension \(n\).
The algorithm will fail if the matrix is not (numerically) strictly positive definite.
Modifications using pivoting are available that can be used for nonnegative definite matrices.
Another option is to factor \(A_\lambda = A + \lambda I\) with \(\lambda > 0\) chosen large enough to make \(A_\lambda\) numerically strictly positive definite.
This is often used in optimization.
4.3.2 Some Applications of the Cholesky Factorization
Solving the normal equations in least squares.
This requires that the predictors be linearly independent
Generating multivariate normal random vectors.
Parameterizing strictly positive definite matrices:
Any lower triangular matrix \(L\) with arbitrary values below the diagonal and positive diagonal entries determines and is uniquely determined by the positive definite matrix \(A = L L^T\)
4.3.3 Cholesky Factorization in R
The function chol computes the Cholesky factorization.
The returned value is the upper triangular matrix \(R = L^T\).
LAPACK is used for the computation.
4.4 QR Factorization
An \(m \times n\) matrix \(A\) with \(m \ge n\) can be written as
\[\begin{equation*} A = Q R \end{equation*}\]
where
\(Q\) is \(m \times n\) with orthonormal columns, i.e. \(Q^T Q = I_n\)
\(R\) is upper triangular
Several algorithms are available for computing the QR decomposition:
Modified Gram-Schmidt;
Householder transformations (reflections);
Givens transformations (rotations).
Each has advantages and disadvantages.
LINPACK dqrdc and LAPACK DGEQP3 use Householder transformations.
The QR decomposition exists regardless of the rank of \(A\).
The rank of \(A\) is \(n\) if and only if the diagonal elements of \(R\) are all non-zero.
4.4.1 Householder Transformations
A Householder transformation is a matrix of the form
\[\begin{equation*} P = I - 2 v v^T/ v^T v \end{equation*}\]
where \(v\) is a nonzero vector.
\(Px\) is the reflection of \(x\) in the hyperplane orthogonal to \(v\).
Given a vector \(x \neq 0\), choosing \(v = x + \alpha e_1\) with
\[\alpha = \pm \|x\|_2\]
and \(e_1\) the first unit vector (first column of the identity) produces
\[Px = \mp\|x\|_2 e_1\]
This can be used to zero all but the first element of the first column of a matrix:
\[\begin{equation*} P \begin{bmatrix} \times & \times & \times\\ \times & \times & \times\\ \times & \times & \times\\ \times & \times & \times\\ \times & \times & \times\\ \end{bmatrix} = \begin{bmatrix} \times & \times & \times\\ 0 & \times & \times\\ 0 & \times & \times\\ 0 & \times & \times\\ 0 & \times & \times\\ \end{bmatrix} \end{equation*}\]
This is the first step in computing the \(QR\) factorization.
The denominator \(v^Tv\) can be written as
\[\begin{equation*} v^Tv = x^Tx + 2 \alpha x_1 + \alpha^2 \end{equation*}\]
Choosing \(\alpha = \text{sign}(x_1)\|x\|_2\) ensures that all terms are non-negative and avoids cancellation.
With the right choice of sign Householder transformations are very stable.
The computation \(Py\) would be carried out without creating the \(P\) matrix:
\[\begin{equation*} Py = (I - 2 v v^T/ v^T v)y = y - \left(2 \frac{v^T y}{v^T v} \right) v. \end{equation*}\]
4.4.2 Givens Rotations
A Givens rotation is a matrix \(G\) that is equal to the identity except for elements \(G_{ii},G_{ij},G_{ji},G_{jj}\), which are
\[\begin{equation*} \begin{bmatrix} G_{ii} & G_{ij} \\ G_{ji} & G_{jj} \end{bmatrix} = \begin{bmatrix} c & s\\ -s & c \end{bmatrix} \end{equation*}\]
with \(c = \cos(\theta)\) and \(s = \sin(\theta)\) for some \(\theta\).
Premultiplication by \(G^T\) is a clockwise rotation by \(\theta\) radians in the \((i,j)\) coordinate plane.
Given scalars \(a,b\) one can compute \(c, s\) so that \[\begin{equation*} \begin{bmatrix} c & s\\ -s & c \end{bmatrix}^T \begin{bmatrix} a\\ b \end{bmatrix} = \begin{bmatrix} r\\ 0 \end{bmatrix} \end{equation*}\]
This allows \(G\) to zero one element while changing only one other element.
A stable way to choose \(c, s\):
\(c = 1; s = 0\)
else
if \(|b| > |a|\)
\(\tau = -a/b; s = 1/\sqrt{1+\tau^2}; c = s\tau\)
else
\(\tau = -b/a;\; c = 1/\sqrt{1 + \tau^2};\; s = c \tau\)
end
end
A sequence of Givens rotations can be used to compute the \(QR\) factorization.
The zeroing can be done working down columns or across rows.
Working across rows is useful for incrementally adding more observations.
4.4.3 Applications
The QR decomposition can be used for solving \(n \times n\) systems of equations
\[\begin{equation*} Ax = b \end{equation*}\]
since \(Q^{-1} = Q^T\) and so
\[\begin{equation*} A x = Q R x = b \end{equation*}\]
is equivalent to the upper triangular system
\[\begin{equation*} R x = Q^T b \end{equation*}\]
The QR decomposition can also be used to solve the normal equations in linear regression:
If \(X\) is the \(n \times p\) design matrix then the normal equations are
\[\begin{equation*} X^T X b = X^T y \end{equation*}\]
If \(X = QR\) is the QR decomposition of \(X\), then \(X^T = R^T Q^T\) and therefore
\[\begin{align*} X^TX &= R^T Q^T Q R = R^T R\\ X^T y &= R^T Q^T y \end{align*}\]
If \(X\) is of full rank then \(R^T\) is invertible, and the normal equations are equivalent to the upper triangular system
\[\begin{equation*} R b = Q^T y \end{equation*}\]
This approach avoids computing \(X^T X\).
If \(X\) is of full rank then \(R^T R\) is the Cholesky factorization of \(X^T X\) (up to multiplications of rows of \(R\) by \(\pm 1\)).
4.4.4 QR with Column Pivoting
Sometimes the columns of \(X\) are linearly dependent or nearly so.
By permuting columns we can produce a factorization
\[\begin{equation*} A = Q R P \end{equation*}\]
where
\(P\) is a permutation matrix
\(R\) is upper triangular and the diagonal elements of \(R\) have non-increasing magnitudes, i.e.
\[|r_{ii}| \ge |r_{jj}|\]
if \(i \le j\).
If some of the diagonal entries of \(R\) are zero, then \(R\) will be of the form
\[\begin{equation*} R = \begin{bmatrix} R_{11} & R_{12}\\ 0 & 0 \end{bmatrix} \end{equation*}\]
where \(R_{11}\) is upper triangular with non-zero diagonal elements non-increasing in magnitude.
The rank of the matrix is the number of non-zero rows in R.
The numerical rank of a matrix can be determined by
computing its QR factorization with column pivoting
specifying a tolerance level \(\epsilon\) such that all diagonal entries \(|r_{ii}| < \epsilon\) are considered numerically zero.
Modifying the computed QR factorization to zero all rows corresponding to numerically zero \(r_{ii}\) values.
4.4.5 Some Regression Diagnostics
The projection matrix, or hat matrix, is
\[\begin{equation*} H = X (X^T X)^{-1} X^T = QR (R^T R)^{-1} R^T Q^T = QQ^T \end{equation*}\]
The diagonal elements of the hat matrix are therefore
\[\begin{equation*} h_i = \sum_{j=1}^p q_{ij}^2 \end{equation*}\]
If \(\hat{e}_i = y_i - \hat{y}_i\) is the residual, then
\[\begin{align*} s_{-i}^2 &= \frac{\text{SSE} - \hat{e}_i^2/(1-h_i)}{n-p-1} = \text{ estimate of variance without obs. $i$}\\ t_i &= \frac{\hat{e}_i}{s_{-i}\sqrt{1-h_i}} = \text{externally studentized residual}\\ D_i &= \frac{\hat{e}_i^2 h_i}{(1-h_i)^2s^2p} = \text{Cook's distance} \end{align*}\]
4.4.6 QR Decomposition and Least Squares in R
The R function qr uses either LINPACK or LAPACK to compute QR
factorizations.
A modified LINPACK routine is the default.
The core linear model fitting function lm.fit uses QR factorization
with column pivoting.
4.5 Singular Value Decomposition
An \(m \times n\) matrix \(A\) with \(m \ge n\) can be factored as
\[\begin{equation*} A = U D V^T \end{equation*}\]
where
\(U\) is \(m \times n\) with orthonormal columns, i.e. \(U^T U = I_n\).
\(V\) is \(n \times n\) orthogonal, i.e. \(V V^T = V^T V = I_n\).
\(D = \text{diag}(d_1,\dots,d_n)\) is \(n \times n\) diagonal with \(d_1 \ge d_2 \ge \dots \ge d_n \ge 0\).
This is the singular value decomposition, or SVD of \(A\).
The values \(d_1, \dots, d_n\) are the singular values of \(A\).
The columns of \(U\) are the right singular vectors of \(A\).
The columns of \(V\) are the left singular vectors of \(A\).
If the columns of \(A\) have been centered so the column sums of \(A\) are zero, then the columns of \(UD\) are the principal components of \(A\).
Excellent algorithms are available for computing the SVD.
These algorithms are usually several times slower than the QR algorithms.
4.5.1 Some Properties of the SVD
The Euclidean matrix norm of \(A\) is defined as
\[\begin{equation*} \Norm{A}_2 = \max_{x \neq 0}\frac{\Norm{Ax}_2}{\Norm{x}_2} \end{equation*}\]
with \(\Norm{x}_2 = \sqrt{x^T x}\) the Euclidean vector norm.
If \(A\) has SVD \(A=UDV^T\), then
\[\begin{equation*} \Norm{A}_2 = d_1 \end{equation*}\]
If \(k < \text{rank}(A)\) and
\[\begin{equation*} A_k = \sum_{i=1}^k d_i u_i v_i^T \end{equation*}\]
where \(u_i\) is the \(i\)-th column of \(U\) and \(v_i\) is the \(i\)-th column of \(V\) then
\[\begin{equation*} \min_{B:\text{rank}(B) \le k} \Norm{A - B}_2 = \Norm{A - A_k} = d_{k+1} \end{equation*}\]
In particular,
\(d_1 u_1 v_1^T\) is the best rank one approximation to \(A\) (in the Euclidean matrix norm).
\(A_k\) is the best rank \(k\) approximation to \(A\).
If \(m = n\) then \(d_n = \min\{d_1,\dots.d_n\}\) is the distance between \(A\) and the set of singular matrices.
If \(A\) is square then the condition number based on the Euclidean norm is
\[\begin{equation*} \kappa_2(A) = \Norm{A}_2\Norm{A^{-1}}_2 = \frac{d_1}{d_n} \end{equation*}\]
For an \(m \times n\) matrix with \(m > n\) we also have
\[\begin{equation*} \kappa_2(A) = \frac{\max_{x \ne 0} \frac{\Norm{Ax}_2}{\Norm{x}_2}} {\min_{x \ne 0} \frac{\Norm{Ax}_2}{\Norm{x}_2}} = \frac{d_1}{d_n} \end{equation*}\]
This can be used to relate \(\kappa_2(A^T A)\) to \(\kappa_2(A)\).
This has implications for regression computations.
The singular values are the non-negative square roots of the eigenvalues of \(A^T A\) and the columns of \(V\) are the corresponding eigenvectors.
4.5.2 Moore-Penrose Generalized Inverse
Suppose \(A\) has rank \(r \le n\) and SVD \(A = U D V^T\). Then
\[\begin{equation*} d_{r+1} = \dots = d_n = 0 \end{equation*}\]
Let
\[\begin{equation*} D^+ = \text{diag}\left(\frac{1}{d_1}, \dots, \frac{1}{d_r}, 0, \dots, 0\right) \end{equation*}\]
and let
\[\begin{equation*} A^+ = V D^+ U^T \end{equation*}\]
Then \(A^+\) satisfies
\[\begin{align*} A A^+ A &= A\\ A^+ A A^+ &= A^+\\ (A A^+)^T &= A A^+\\ (A^+A)^T &= A^+ A \end{align*}\]
\(A^+\) is the unique matrix with these properties and is called the Moore-Penrose generalized inverse or pseudo-inverse.
4.5.3 SVD and Least Squares
If \(X\) is an \(n \times p\) design matrix of less than full rank, then there are infinitely many values of \(b\) that minimize
\[\begin{equation*} \Norm{y - Xb}_2^2 \end{equation*}\]
Among these solutions,
\[\begin{equation*} b = (X^T X)^+ X^T y \end{equation*}\]
minimizes \(\Norm{b}_2\).
This is related to penalized regression where one might choose \(b\) to minimize
\[\begin{equation*} \Norm{y - Xb}_2^2 + \lambda \Norm{b}_2^2 \end{equation*}\]
for some choice of \(\lambda > 0\).
4.5.4 SVD and Principal Components Analysis
Let \(X\) be an \(n \times p\) matrix of \(n\) observations on \(p\) variables.
Principal components analysis involves estimating the eigenvectors and eigenvalues of the covariance matrix.
Let \(\widetilde{X}\) be the data matrix with columns centered at zero by subtracting the column means.
The sample covariance matrix is
\[\begin{equation*} S = \frac{1}{n-1} \widetilde{X}^T\widetilde{X} \end{equation*}\]
Let \(\widetilde{X} = U D V^T\) be the SVD of the centered data matrix \(\widetilde{X}\).
Then
\[\begin{equation*} S = \frac{1}{n-1} V D U^T U D V^T = \frac{1}{n-1} V D^2 V^T \end{equation*}\]
The diagonal elements of \(\frac{1}{n-1}D^2\) are the eigenvalues of \(S\).
The columns of \(V\) are the eigenvectors of \(S\).
Using the SVD of \(\widetilde{X}\) is more numerically stable than
forming \(\widetilde{X}^T\widetilde{X}\)
computing the eigenvalues and eigenvectors.
4.5.5 SVD and Numerical Rank
The rank of a matrix \(A\) is equal to the number of non-zero singular values.
Exact zeros may not occur in the SVD due to rounding.
Numerical rank determination can be based on the SVD. All \(d_i \le \delta\) can be set to zero for some choice of \(\delta\). Golub and van Loan recommend using
\[\delta = \mathbf{u}\Norm{A}_\infty\]
If the entries of \(A\) are only accurate to \(d\) decimal digits, then Golub and van Loan recommend
\[\begin{equation*} \delta = 10^{-d} \Norm{A}_\infty \end{equation*}\]
If the numerical rank of \(A\) is \(\hat{r}\) and \(d_{\hat{r}} \gg \delta\) then \(\hat{r}\) can be used with some confidence; otherwise caution is needed.
4.5.6 Other Applications
The SVD is used in many areas of numerical analysis.
It is also often useful as a theoretical tool.
Some approaches to compressing \(m \times n\) images are based on the SVD.
A simple example using the
volcano
data:
s <- svd(volcano)
head(s$d, 10)
## [1] 9644.28782 488.60992 341.18358 298.76602 141.83363
## [6] 72.12443 43.55698 33.52319 27.38376 19.97622
tail(s$d, 2)
## [1] 1.0526941 0.9545092The relative error in the final image is 0.056.
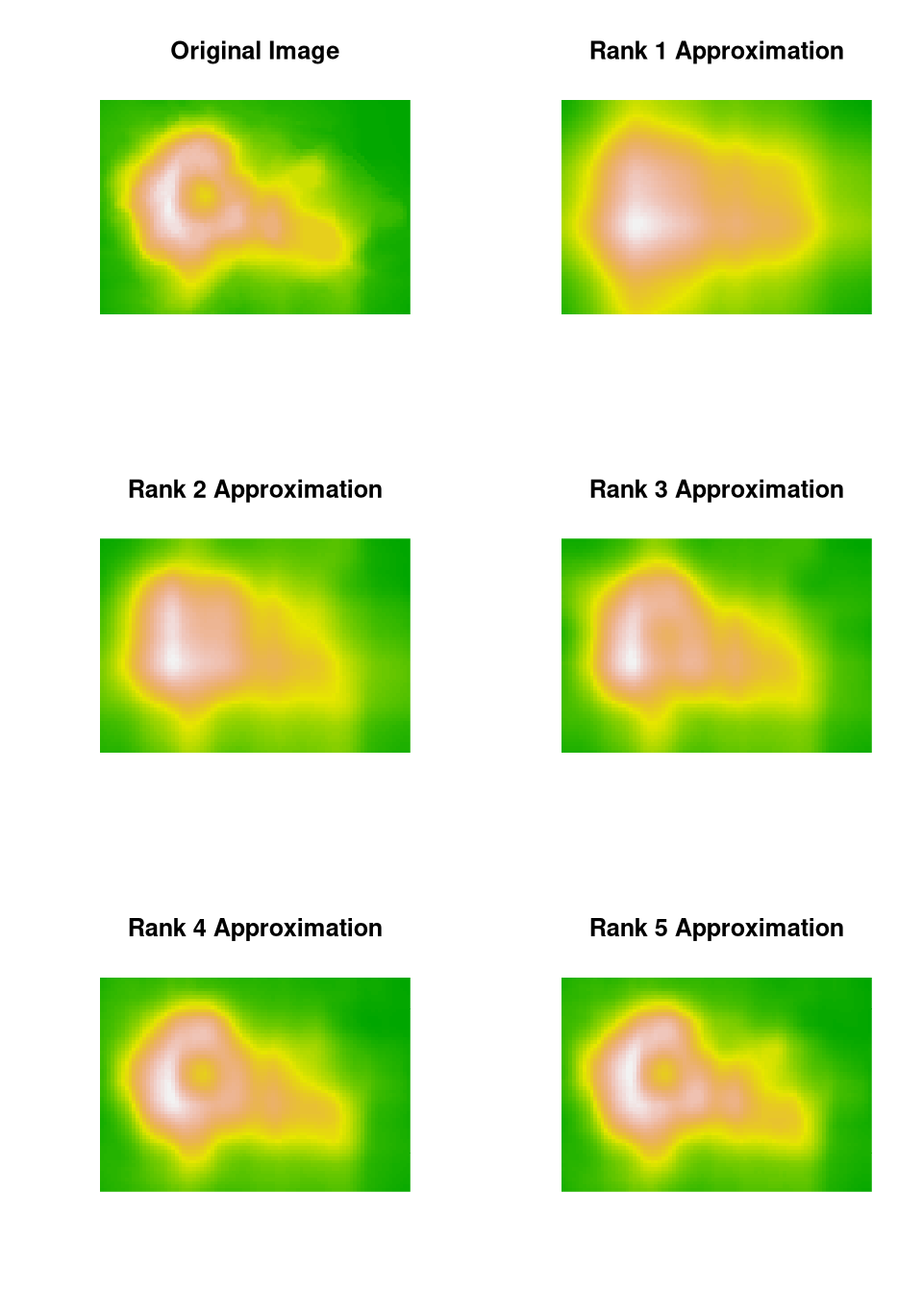
4.5.7 SVD in R
R provides the function svd to compute the SVD.
The implementation uses LAPACK.
You can ask for the singular values only; this is will be faster for larger problems.
4.6 Eigenvalues and Eigenvectors
Let \(A\) be an \(n \times n\) matrix. \(\lambda\) is an eigenvalue of \(A\) if
\[\begin{equation*} A v = \lambda v \end{equation*}\]
for some \(v \neq 0\); \(v\) is an eigenvector or \(A\).
If \(A\) is a real \(n \times n\) matrix then it has \(n\) eigenvalues.
Several eigenvalues may be identical.
Some eigenvalues may be complex; if so, then they come in conjugate pairs.
The set of eigenvalues is called the spectrum.
If \(A\) is symmetric then the eigenvalues are real.
If \(A\) is symmetric then
\(A\) is strictly positive definite if and only if all eigenvalues are positive.
\(A\) is positive semi-definite if and only if all eigenvalues are non-negative.
There exists an orthogonal matrix \(V\) such that
\[ A = V \Lambda V^T \]
with \(\Lambda = \text{diag}(\lambda_1,\dots,\lambda_n)\); the columns of \(V\) are the corresponding normalized eigenvectors.
This is called the spectral decomposition of \(A\).
Some problems require only the largest eigenvalue or the largest few; sometimes the corresponding eigenvectors are also needed.
The stationary distribution of an irreducible finite state-space Markov chain is the unique eigenvector, normalized to sum to one, corresponding to the largest eigenvalue \(\lambda = 1\).
The speed of convergence to the stationary distribution depends on the magnitude of the second largest eigenvalue.
The R function eigen can be used to compute eigenvalues and,
optionally, eigenvectors.
The package svd provides routines for computing a specified number
of the largest eigenvalues and corresponding eigenvectors.
4.7 Determinants
Theoretically the determinant can be computed as the product of
the diagonals of \(U\) in the \(PLU\) decomposition;
the squares of the diagonals of \(L\) in the Cholesky factorization;
the diagonals of R in the QR decomposition;
the eigenvalues.
Numerically these are almost always bad ideas.
It is almost always better to work out the sign and compute the sum of the logarithms of the magnitudes of the factors.
The R functions det and determinant compute the determinant.
determinant is more complicated to use, but has a logarithm option.
Likelihood and Bayesian analyses often involve a determinant.
Usually the log likelihood and log determinant should be used.
Usually the log determinant can be computed from a decomposition needed elsewhere in the log likelihood calculation, e.g. a Cholesky factorization.
4.7.1 Example: Multivariate Normal Log-Likelihood Computation
The density at \(x\) of a \(d\)-dimensional normal distribution with mean vector \(\mu\) and covariance matrix \(C\) is
\[\begin{equation*} \frac{1}{\sqrt{(2 \pi)^d \det{C}}} \exp\left\{-\frac{1}{2} (x - \mu)^T C^{-1} (x - \mu)\right\}. \end{equation*}\]
The log-density (dropping the additive constant) is
\[\begin{equation*} -\frac{1}{2} \log\det{C} -\frac{1}{2} (x - \mu)^T C^{-1} (x - \mu). \end{equation*}\]
If \(C = L L^T\) is the Cholesky factorization of \(C\), then \(C^{-1} = L^{-T}L^{-1}\) and the quadratic form is
\[\begin{equation*} (x - \mu)^T C^{-1} (x - \mu) = (x - \mu)^T L^{-T}L^{-1} (x - \mu) = \|L^{-1} (x - \mu)\|_2^2. \end{equation*}\]
So to compute the log density at \(x\):
Compute \(y = L^{-1} (x - \mu)\) by solving \(L y = (x - \mu)\) for \(y\).
Compute \(\frac{1}{2} \log\det{C} = \log \det{L}\), which is the sum of the logarithms of the diagonal elements of \(L\).
If \(C^{-1}\) is given, then the Colesky factorization of \(C^{-1}\) can be used to compute
\[\begin{equation*} \log\det{C} = -\log\det{C^{-1}}. \end{equation*}\]
4.8 Non-Negative Matrix Factorization
A number of problems lead to the desire to approximate a non-negative matrix \(X\) by a product
\[\begin{equation*} X \approx W H \end{equation*}\]
where \(W\), \(H\) are non-negative matricies of low rank, i.e. with few columns.
There are a number of algorithms available, most of the form
\[\begin{equation*} \min_{W, H} [D(X, WH) + R(W, H)] \end{equation*}\]
where \(D\) is a loss function and \(R\) is a possible penalty for encouraging desirable characteristics of \(W\) and \(H\), such as smoothness or sparseness.
The R package NMF provides one approach, and a vignette in the
package provides some background and references.
As an example, using default settings in the NMF package the volcano
image can be approximated with factorizations of rank \(1, \dots, 5\) by
library(NMF)
nmf1 <- nmf(volcano, 1); V1 <- nmf1@fit@W %*% nmf1@fit@H
nmf2 <- nmf(volcano, 2); V2 <- nmf2@fit@W %*% nmf2@fit@H
nmf3 <- nmf(volcano, 3); V3 <- nmf3@fit@W %*% nmf3@fit@H
nmf4 <- nmf(volcano, 4); V4 <- nmf4@fit@W %*% nmf4@fit@H
nmf5 <- nmf(volcano, 5); V5 <- nmf5@fit@W %*% nmf5@fit@HThe relative error for the final image is
max(abs(volcano - V5)) / max(abs(volcano))
## [1] 0.03096702The images:
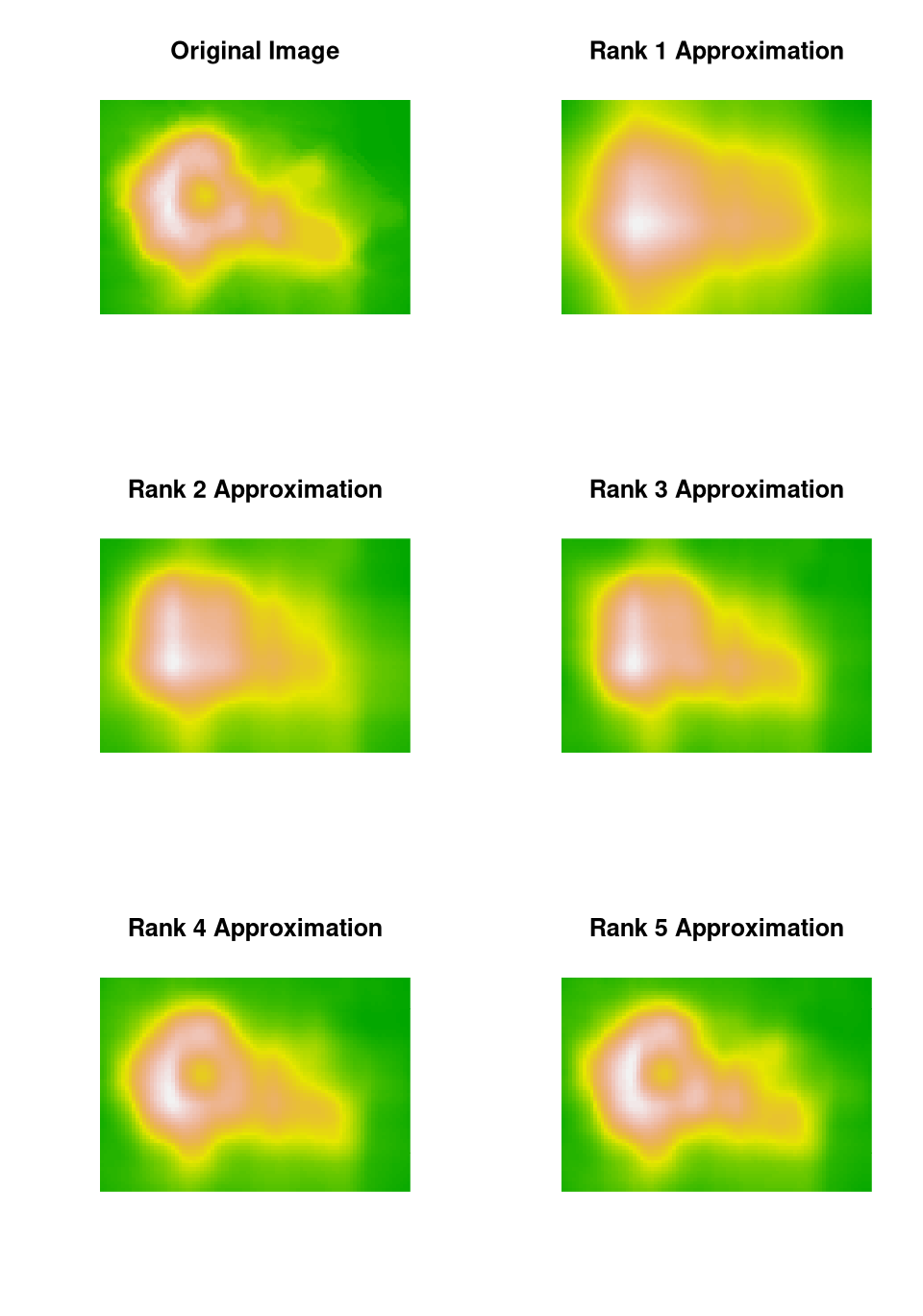
Another application is recommender systems.
For example, \(X\) might be ratings of movies (columns) by viewers (rows).
The set of actual values would be very sparse as each viewer will typically rate only a small subset of all movies.
\(W\) would be a user preference matrix, \(H\) a corresponding movie feature matrix.
The product \(WH\) would provide predicted ratings for movies the users have not yet seen.
4.9 Other Factorizations
Many other factorizations of matrices are available and being developed.
Some examples are
Robust variants of the SVD
Sparse variants, e.g. Dan Yang, Zongming Ma, and Andreas Buja (2014), “A Sparse Singular Value Decomposition Method for High-Dimensional Data,” Journal of Computational and Graphical Statistics 23(4), 923–942.
Constrained factorizations, e.g. C. Ding, T. Li, and M. I. Jordan (2010), “Convex and Semi-Nonnegative Matrix Factorizations,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 32(1), 45–55.
4.10 Exploiting Special Structure
Specialized algorithms can sometimes be used for matrices with special structure.
4.10.1 Toeplitz Systems
Stationary time series have covariance matrices that look like
\[\begin{equation*} \begin{bmatrix} \sigma_0 & \sigma_1 & \sigma_2 & \sigma_3 & \dots\\ \sigma_1 & \sigma_0 & \sigma_1 & \sigma_2 & \dots\\ \sigma_2 & \sigma_1 & \sigma_0 & \sigma_1 & \dots\\ \sigma_3 & \sigma_2 & \sigma_1 & \sigma_0 & \ddots\\ \ddots & \ddots & \ddots & \ddots & \ddots & \end{bmatrix} \end{equation*}\]
This is a Toeplitz matrix.
This matrix is also symmetric — this is not required for a Toeplitz matrix.
Special algorithms requiring \(O(n^2)\) operations are available for Toeplitz systems.
General Cholesky factorization requires \(O(n^3)\) operations.
The R function toeplitz creates Toeplitz matrices.
4.10.2 Circulant Systems
Some problems give rise to matrices that look like
\[\begin{equation*} C_n = \begin{bmatrix} a_1 & a_2 & a_3 & \dots & a_n\\ a_n & a_1 & a_2 & \dots & a_{n-1}\\ a_{n-1} & a_n & a_1 & \dots & a_{n-2}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ a_2 & a_3 & a_4 & \dots & a_1 \end{bmatrix} \end{equation*}\]
This is a circulant matrix, a subclass of Toeplitz matrices.
Circulant matrices satisfy
\[\begin{equation*} C_n = F_n^* \, \text{diag}(\sqrt{n} F_n a) \, F_n \end{equation*}\]
where \(F_n\) is the Fourier matrix with
\[\begin{equation*} F_n(j,k) = \frac{1}{\sqrt{n}}e^{-(j-1)(k-1)2\pi\sqrt{-1}/n} \end{equation*}\]
and \(F_n^*\) is the conjugate transpose, Hermitian transpose, or adjoint matrix of \(F_n\).
The eigen values are the elements of \(\sqrt{n} F_n a\).
Products \(F_n\, x\) and \(F_n^* x\) can be computed with the fast Fourier transform (FFT).
In R \[\begin{align*} \sqrt{n} F_n x &= \texttt{fft(x)}\\ \sqrt{n} F_n^* x &= \texttt{fft(x, inverse = TRUE)}\\ \end{align*}\]
These computations are generally \(O(n \log n)\) in complexity.
Circulant systems can be used to approximate other systems.
Multi-dimensional analogs exist as well.
A simple example is available on line.
4.10.3 Sparse Systems
Many problems lead to large systems in which only a small fraction of coefficients are non-zero.
Some methods are available for general sparse systems.
Specialized methods are available for structured sparse systems such as
tri-diagonal systems;
block diagonal systems;
banded systems.
Careful choice of row and column permutations can often turn general sparse systems into banded ones.
4.10.4 Sparse and Structured Systems in R
Sparse matrix support in R is improving.
Some packages, like nlme, provide utilities they need.
One basic package available on CRAN is
sparseM.
A more extensive package is Matrix.
Matrix is the engine for mixed effects/multi-level model fitting in
lme4.
4.10.5 Update Formulas
Update formulas are available for most decompositions that allow for efficient adding or dropping of rows or columns.
These can be useful for example in cross-validation and variable selection computations.
They can also be useful for fitting linear models to very large
data sets; the package biglm uses this approach.
I am not aware of any convenient implementations in R at this point but they may exist.
4.11 Iterative Methods
Iterative methods can be useful in large, sparse problems.
Iterative methods for sparse problems can also often be parallelized effectively.
Iterative methods are also useful when
\(A x\) can be computed efficiently for any given \(x\), but
it is expensive or impossible to compute \(A\) explicitly.
Some simple examples are available on line.
4.11.1 Gauss-Seidel Iteration
Choose an initial solution \(x^{(0)}\) to \[\begin{equation*} Ax = b \end{equation*}\]
and then update from \(x^{(k)}\) to \(x^{(k+1)}\) by
\[\begin{equation*} x^{(k+1)}_i = \frac{1}{a_{ii}} \left(b_i - \sum_{j=1}^{i-1} a_{ij} x_{j}^{(k+1)} - \sum_{j=i+1}^n a_{ij} x_{j}^{(k)}\right) \end{equation*}\]
for \(i = 1, \dots, n\).
This is similar in spirit to Gibbs sampling.
This can be written in matrix form as \[\begin{equation*} x^{(k+1)} = (D+L)^{-1}(-Ux^{(k)}+b) \end{equation*}\] with \[\begin{align*} L &= \begin{bmatrix} 0 & 0 & \dots & \dots & 0\\ a_{21} & 0 & \dots & & \vdots\\ a_{31} & a_{32} & \ddots & & 0\\ \vdots & & & 0 & 0 \\ a_{n1} & a_{n2} & \dots & a_{n,n-1} & 0 \end{bmatrix}\\ D &= \text{diag}(a_{11},\dots, a_{nn})\\ U &= \begin{bmatrix} 0 & a_{12} & \dots & \dots & a_{1n}\\ 0 & 0 & \dots & & \vdots\\ 0 & 0 & \ddots & & a_{n-2,n}\\ \vdots & & & & a_{n-1,n}\\ 0 & 0 & \dots & 0 & 0 \end{bmatrix} \end{align*}\]
4.11.2 Splitting Methods
The Gauss-Seidel method is a member of a class of splitting methods where
\[\begin{equation*} M x^{(k+1)} = N x^{(k)} + b \end{equation*}\] with \(A = M - N\).
For the Gauss-Seidel method \[\begin{align*} M &= D + L\\ N &= -U. \end{align*}\]
Other members include Jacobi iterations with \[\begin{align*} M_J &= D\\ N_J &= -(L+U) \end{align*}\]
Splitting methods are practical if solving linear systems with matrix \(M\) is easy.
4.11.3 Convergence
A splitting method for a non-singular matrix \(A\) will converge to the unique solution of \(Ax=b\) if
\[\begin{equation*} \rho(M^{-1} N) < 1 \end{equation*}\]
where
\[\begin{equation*} \rho(G) = \max\{|\lambda|: \text{$\lambda$ is an eigenvalue of $G$}\} \end{equation*}\]
is the spectral radius of \(G\).
This is true, for example, for the Gauss-Seidel method if \(A\) is strictly positive definite.
Convergence can be very slow if \(\rho(M^{-1} N)\) is close to one.
4.11.4 A Simple Example
A simple implementation of Gauss-Seidel iteration using the splitting representation:
gssolve <- function(A, b, itermax = length(b),
tol = sqrt(.Machine$double.eps)) {
n <- length(b)
M <- A; M[rep(1:n, n) < rep(1:n, each = n)] <- 0
N <- -A; N[rep(1:n, n) >= rep(1:n, each = n)] <- 0
x <- numeric(n)
for (i in seq_len(itermax)) {
x.old <- x
x <- forwardsolve(M, N %*% x + b)
if (max(abs(x - x.old) / (tol + abs(x.old))) < tol &&
max(abs(A %*% x - b)) < tol) {
message(i, " iterations")
return(x)
}
}
message("iteration limit reached")
x
}With a well-conditioned matrix Gauss-Seidel iteration can be faster than a dense PLU decomposition.
n <- 2000
A <- crossprod(matrix(rnorm(n * n), n)) / n + 5 * diag(n)
b <- rnorm(n)
system.time(solve(A, b))
## user system elapsed
## 1.632 0.114 0.147
system.time(gssolve(A, b))
## 13 iterations
## user system elapsed
## 1.287 0.009 0.274Whether the Gauss-Seidel method is faster on this example may depend on the the BLAS/LAPACK in use:
sessionInfo()$BLAS
## [1] "/usr/lib64/libflexiblas.so.3.1"
sessionInfo()$LAPACK
## [1] "/usr/lib64/libflexiblas.so.3.1"4.11.5 Successive Over-Relaxation
A variation is to define
\[\begin{equation*} x^{(k+1)}_i = \frac{\omega}{a_{ii}} \left(b_i - \sum_{j=1}^{i-1} a_{ij} x_{j}^{(k+1)} - \sum_{j=i+1}^n a_{ij} x_{j}^{(k)}\right) + (1-\omega) x^{(k)}_i \end{equation*}\]
or, in matrix form,
\[\begin{equation*} M_\omega x^{(k+1)} = N_\omega x^{(k)} + \omega b \end{equation*}\]
with
\[\begin{align*} M_\omega &= D + \omega L\\ N_\omega &= (1-\omega)D - \omega U \end{align*}\]
for some \(\omega\), usually with \(0 < \omega < 1\).
This is called successive over-relaxation (SOR), from its first application in a structural engineering problem.
For some choices of \(\omega\) we can have
\[\begin{equation*} \rho(M_\omega^{-1}N_\omega) \ll \rho(M^{-1}N) \end{equation*}\]
and thus faster convergence.
For some special but important problems the value of \(\omega\) that minimizes \(\rho(M_\omega^{-1}N_\omega)\) is known or can be computed.
4.11.6 Conjugate Gradient Method
If \(A\) is symmetric and strictly positive definite then the unique solution to \(Ax=b\) is the unique minimizer of the quadratic function \[\begin{equation*} f(x) = \frac{1}{2}x^T A x - x^T b \end{equation*}\] Any nonlinear or quadratic optimization method can be used to find the minimum.
The most common one used in this context is the conjugate gradient method.
Choose an initial \(x_0\), set \(d_0 = -g_0 = b - A x_0\).
Then, while \(g_k \neq 0\), for \(k = 0, 1, \dots\) compute \[\begin{align*} \alpha_k &= -\frac{g_k^T d_k}{d_k^T A d_k}\\ x_{k+1} &= x_k + \alpha_k d_k\\ g_{k+1} &= A x_{k+1} - b\\ \beta_{k+1} &= \frac{g_{k+1}^T A d_k}{d_k^T A d_k}\\ d_{k+1} &= -g_{k+1} + \beta_{k+1} d_k \end{align*}\]
Some properties:
An alternate form of \(g_{k+1}\) is
\[ g_{k+1} = g_k + \alpha_k A d_k \]
This means only one matrix-vector multiplication is needed per iteration.
The vector \(g_k\) is the gradient of \(f\) at \(x_k\).
The initial direction \(d_0 = -g_0\) is the direction of steepest descent from \(x_0\)
The directions \(d_0, d_1, \dots\) are \(A\)-conjugate, i.e. \(d_i^T A d_j = 0\) for \(i \neq j\).
The directions \(d_0, d_1, \dots, d_{n-1}\) are linearly independent.
4.11.7 Convergence
With exact arithmetic,
\[\begin{equation*} A x_n = b \end{equation*}\]
That is, the conjugate gradient algorithm terminates with the exact solution in \(n\) steps.
Numerically this does not happen.
Numerically, the directions will not be exactly \(A\)-conjugate.
A convergence tolerance is used for termination; this can be based on the relative change in the solution
\[\begin{equation*} \frac{\Norm{x_{k+1}-x_{k}}}{\Norm{x_k}} \end{equation*}\]
or the residual or gradient
\[\begin{equation*} g_k = A x_k - b \end{equation*}\]
or some combination; an iteration count limit is also a good idea.
If the algorithm does not terminate within \(n\) steps it is a good idea to restart it with a steepest descent step from the current \(x_k\).
In many sparse and structured problems the algorithm will terminate in far fewer than \(n\) steps for reasonable tolerances.
Convergence is faster if the condition number of \(A\) is closer to one.
The error can be bounded as
\[\begin{equation*} \Norm{x - x_k}_A \leq 2 \Norm{x - x_0}_A \left(\frac{\sqrt{\kappa_2(A)} - 1}{\sqrt{\kappa_2(A)} + 1}\right)^k \end{equation*}\]
with \(\Norm{x}_A = \sqrt{x^T A x}\).
Preconditioning strategies can improve convergence.
These transform the original problem to one with \(\tilde{A} = C^{-1} A C^{-1}\) for some symmetric strictly positive definite \(C\), and then use the conjugate gradient method for \(\tilde{A}\)
Simple choices of \(C\) are most useful; sometimes a diagonal matrix will do.
Good preconditioners can sometimes be designed for specific problems.
4.11.8 A Simple Implementation
cg <- function(A, b, x, done) {
dot <- function(x, y) crossprod(x, y)[1]
n <- 0
g <- A(x) - b
d <- -g
repeat {
h <- A(d)
u <- dot(d, h)
a <- -dot(g, d) / u
n <- n + 1
x.old <- x
x <- x + a * d
g <- g + a * h
b <- dot(h, g) / u
d <- -g + b * d
if (done(g, x, x.old, n))
return(list(x = as.vector(x),
g = as.vector(g),
n = n))
}
}The linear transformation and the termination condition are specified as functions.
The termination condition can use a combination of the gradient, current solution, previous solution, or iteration count.
A simple example:
X <- crossprod(matrix(rnorm(25), 5))
y <- rnorm(5)
cg(A = function(x) X %*% x,
b = y,
x = rep(0, 5),
done = function(g, x, x.old, n) n >= 5)
## $x
## [1] -2.004109 -8.240581 4.410103 -6.264520 -2.547753
##
## $g
## [1] -2.148282e-14 5.370704e-15 -3.844147e-14 -2.416123e-14
## [5] -1.865175e-14
##
## $n
## [1] 5
solve(X, y)
## [1] -2.004109 -8.240581 4.410103 -6.264520 -2.547753A simple conjugate gradient based cgsolve function might be
defined as
cgsolve <- function(X, y, tol = sqrt(.Machine$double.eps)) {
A <- function(x)
X %*% x
done <- function(g, x, x.old, n)
n >= length(x) ||
(max(abs(x - x.old) / (tol + abs(x.old))) < tol &&
max(abs(g)) < tol)
x <- rep(0, length(y))
v <- cg(A, y, x, done = done)
if (v$n >= length(y))
message("iteration limit reached")
else
message(v$n, " iterations")
v$x
}With a positive definite matrix with a large diagonal component
cgsolve can be very effective:
N <- 2000
X <- crossprod(matrix(rnorm(N * N), N))
XX <- X / N + 5 * diag(N)
y <- rnorm(N)
system.time(v0 <- solve(XX, y))
## user system elapsed
## 1.047 0.043 0.096
system.time(v <- cgsolve(XX, y))
## 15 iterations
## user system elapsed
## 0.583 0.000 0.044
max(abs((v - v0)/ v0))
## [1] 3.659718e-094.12 Linear Algebra Software
4.12.1 Some Standard Packages
Open source packages developed at national laboratories:
LINPACK for linear equations and least squares
EISPACK for eigenvalue problems
LAPACK newer package for linear equations and eigenvalues
Designed for high performance. Available from Netlib at http://www.netlib.org/
Commercial packages:
IMSL used more in US
NAG used more in UK
…
4.12.2 BLAS: Basic Linear Algebra Subroutines
Modern BLAS has three levels:
Level 1: Vector and vector/vector operations such as
- dot product \(x^T y\);
- scalar multiply and add (axpy): \(\alpha x + y\);
- Givens rotations;
- …
Level 2: Matrix/vector operations, such as \(A x\)
Level 3: Matrix/matrix operations, such as \(A B\)
LINPACK uses only Level 1; LAPACK uses all three levels.
BLAS defines the interface.
Standard reference implementations are available from Netlib.
Highly optimized versions are available from hardware vendors and research organizations.
4.12.3 Cholesky Factorization in LAPACK
The core of the
DPOTRF
subroutine:
*
* Compute the Cholesky factorization A = L*L'.
*
DO 20 J = 1, N
*
* Compute L(J,J) and test for non-positive-definiteness.
*
AJJ = A( J, J ) - DDOT( J-1, A( J, 1 ), LDA, A( J, 1 ),
$ LDA )
IF( AJJ.LE.ZERO ) THEN
A( J, J ) = AJJ
GO TO 30
END IF
AJJ = SQRT( AJJ )
A( J, J ) = AJJ
*
* Compute elements J+1:N of column J.
*
IF( J.LT.N ) THEN
CALL DGEMV( 'No transpose', N-J, J-1, -ONE, A( J+1, 1 ),
$ LDA, A( J, 1 ), LDA, ONE, A( J+1, J ), 1 )
CALL DSCAL( N-J, ONE / AJJ, A( J+1, J ), 1 )
END IF
20 CONTINUE
DDOT and DSCAL are Level 1 BLAS routines
DGEMV is a Level 2 BLAS routine
4.12.4 ATLAS: Automatically Tuned Linear Algebra Software
Available at http://math-atlas.sourceforge.net/.
Analyzes machine for properties such as cache characteristics.
Runs extensive tests to determine performance trade-offs.
Creates Fortran and C versions of BLAS and some LAPACK routines tailored to the particular machine.
Provides some routines that take advantage of multiple processors using worker threads.
4.12.5 OpenBLAS
Another high-performance BLAS library was developed and maintained by Kazushige Goto.
This is now being developed and maintained as the OpenBLAS roject, available from https://github.com/xianyi/OpenBLAS.
Also provides versions that take advantage of multiple processors.
4.12.6 Vendor Libraries
Intel provides the Math Kernel Libraries (MKL)
AMD has a similar library.
Apple provides accelerated BLAS libraries for its platforms.
4.12.7 Using a High-Performance BLAS with R
R comes with a basic default BLAS.
R can be built to use a specified BLAS.
Once built one can change the BLAS R uses by replacing the shared library R uses.
Some simple computations using the default and MKL vendor BLAS for the data
N <- 1000
X <- matrix(rnorm(N^2), N)
XX <- crossprod(X)Results:
| Timing Expression | Reference | MKL/SEQ | MKL/THR |
|---|---|---|---|
system.time(for (i in 1:5) crossprod(X))} |
2.107 | 0.405 | 0.145 |
system.time(for (i in 1:5) X %*% X) |
3.401 | 0.742 | 0.237 |
system.time(svd(X)) |
3.273 | 0.990 | 0.542 |
system.time(for (i in 1:5) qr(X)) |
2.290 | 1.094 | 1.107 |
system.time(for (i in 1:5) qr(X, LAPACK=TRUE)) |
2.629 | 0.834 | 0.689 |
system.time(for (i in 1:20) chol(XX)) |
2.824 | 0.556 | 0.186 |
These results were obtained using the non-threaded and threaded Intel Math Kernel Library (MKL) and the development version of R a year or two ago.
Versions of the current R using MKL for BLAS may be available as
/group/statsoft/R-patched/build-MKL-seq/bin/R
/group/statsoft/R-patched/build-MKL-thr/bin/RCurrently the standard version of R on our Linux systems seems to be using OpenBLAS.
4.13 Final Notes
Most reasonable approaches will be accurate for reasonable problems.
Choosing good scaling and centering can make problems more reasonable (both numerically and statistically)
Most methods are efficient enough for our purposes.
In some problems worrying about efficiency is important if reasonable problem sizes are to be handled.
Making sure you are using the right approach to the right problem is much more important than efficiency.
Some quotes:
D. E. Knuth, restating a comment by C. A. R. Hoare:
We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil.
W. A. Wulf:
More computing sins are committed in the name of efficiency (without necessarily achieving it) than for any other single reason — including blind stupidity.