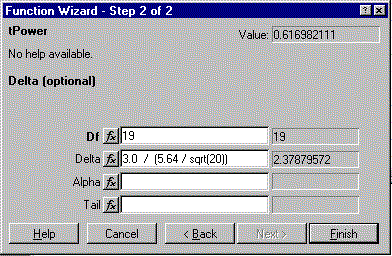
Figure 1: Power analysis using the function wizard.
Versions 5 and later of Excel (on either the Windows or MacIntosh platforms) include a version of Microsoft's Visual Basic (VB) language. This makes it easy to incorporate new functions for special purposes. Moreover, these can be saved as ``add-in'' modules that can be automatically loaded whenever Excel is started.
So, to incorporate power-analysis capabilities into Excel, it is a simple matter to translate an existing algorithm into VB. For example, the Applied Statistics [Lenth(1989)] Fortran code for the non-central t distribution was ported to VB. The result is a function named tPower that takes as arguments the degrees of freedom, non-centrality parameter, the size of the test, and a code (-1, +1, or 0) for whether the test is left-, right-, or two-tailed. This function can be called in formulas entered in one or more cells of the spreadsheet, just like any built-in function. Conveniently, VB provides for default values of omitted arguments. In the case of tPower, the only required argument is the degrees of freedom; the remaining arguments default to 0, .05, and 0 respectively.

Figure 1: Power analysis using the function wizard.
In Excel, the very existence of a function is enough to have a primitive
GUI for it, in the form of the ``function wizard.''
The wizard interface for tPower is shown in Figure 1.
In this illustration, the context is a paired t test for the
difference in electric-blanket-temperature preferences of married couples.
Based on a pilot study, we estimate the standard deviation of the pairwise
differences to be 5.6 degrees Fahrenheit. A mean difference of 3.0 degrees
is considered to be practically significant. We find that with 20 couples,
the power of the paired t test for this effect size is about 62%.
If the goal is a power of 80%, we need a few more couples.
Here, we have 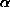 defaulting to .05, and a
default two-tailed test.
defaulting to .05, and a
default two-tailed test.
The function-wizard interface does require some degree of expertise, though it is adequate for some users and some situations (in Figure 1, the form of the non-centrality parameter is similar to that of the t statistic itself). For most users, a more sophisticated interface is needed. Fortunately, Excel supplies a number of GUI objects (radio buttons, macro buttons, etc.) that can be embedded in a workbook and used in conjunction with formula cells. Such a workbook, once developed, can be saved and reused in a variety of situations.
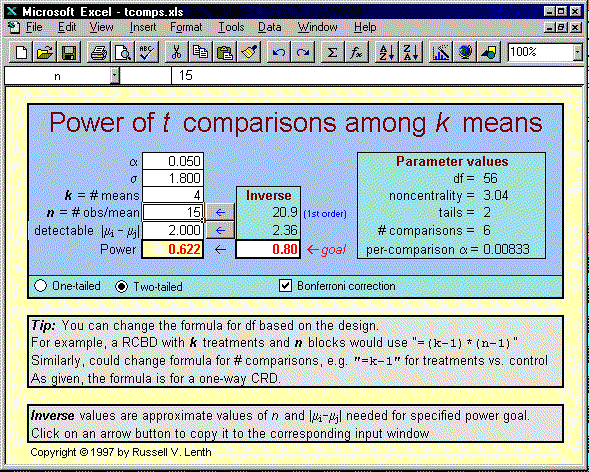
Figure 2: Excel workbook for pairwise t comparisons.
Figure 2 shows such an implementation. This workbook is designed to be used to plan for pairwise comparisons among several means, based on a t statistic. Radio buttons are used to determine whether it is a one- or two-tailed test, and a check box determines whether or not a Bonferroni-corrected critical value is used. (With some additional programming, one could add a function for finding critical values of the Studentized range distribution, and add the HSD critical value as an option.)
The white-colored cells are places where the user can enter parameters of the test, and the right-hand block of cells contain information about the parameters passed to tPower. In the middle (labeled ``Inverse'') are ``what if?'' values for effect size and sample size for a given target power. There we find that, for example, a sample size of about n=21 per treatment would be required to achieve a per-comparison power of 80% (based on a Bonferroni-corrected per-comparison significance level). Clicking on the macro button to the left of this inverse-n cell will enter it into the regular input cell for n.
This workbook is set up for a one-way completely randomized design. For some other design (say a randomized complete-block design with n blocks), the only difference is the degrees of freedom; and this can easily be changed by changing the formula in the cell near the upper right corner. Similarly, one can change the formula for the number of comparisons used in the Bonferroni correction. This direct access to formulas, with immediate updating of results, makes for a powerful and versatile user interface. Unfortunately, it can also lead to trouble when one inadvertently overwrites a formula with an inappropriate entry. It is possible to protect certain cells while allowing inputs in others---a recommended practice.