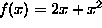 over the
range
over the
range 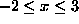 . We can do this by first defining a function
f and then using plot-function:
. We can do this by first defining a function
f and then using plot-function:
Suppose you would like to plot the function 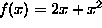 over the
range
over the
range 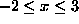 . We can do this by first defining a function
f and then using plot-function:
. We can do this by first defining a function
f and then using plot-function:
(defun f (x) (+ (* 2 x) (^ x 2))) (plot-function #'f -2 3)This is not too hard, but it nevertheless involves one unnecessary step: naming the function f. You probably won't need this function again; it is a throw-away function defined only to allow you to give it to plot-function as an argument. It would be nice if you could just give plot-function an expression that constructs the function you want. Here is such an expression:
(function (lambda (x) (+ (* 2 x) (^ x 2))))
There are two steps involved. The first is to specify the definition of your function. This is done using a lambda expression, in this case
(lambda (x) (+ (* 2 x) (^ x 2)))A lambda expression is a list starting with the symbol lambda, followed by the list of arguments and the expressions making up the body of the function. The lambda expression is only a definition, it is not yet a function, a piece of code that can be applied to arguments. The special form function takes the lambda list and constructs such a function. The result can be saved in a variable or it can be passed on to another function as an argument. For our plotting problem you can use the single expression
(plot-function (function (lambda (x) (+ (* 2 x) (^ x 2)))) -2 3)or, using the #' short form,
(plot-function #'(lambda (x) (+ (* 2 x) (^ x 2))) -2 3)Since the function used in these expressions is never named it is sometimes called an anonymous function.
You can also construct a rotating plot of a function of two variables using the function spin-function. As an example, the expression
(spin-function #'(lambda (x y) (+ (^ x 2) (^ y 2))) -1 1 -1 1)

Figure 17: Rotatable plot of 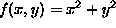 .
.
constructs a plot of the function 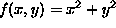 over the
range
over the
range 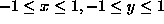 using a
using a 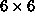 grid.
The number of grid points can be changed using the :num-points
keyword. The result is shown in Figure 17. Again it convenient
to use a lambda expression to specify the function to be plotted.
grid.
The number of grid points can be changed using the :num-points
keyword. The result is shown in Figure 17. Again it convenient
to use a lambda expression to specify the function to be plotted.
There are a number of other situations in which you might want to pass a function on as an argument without first going through the trouble of thinking up a name for the function and defining it using defun. A few additional examples are given in the next subsection.