Advanced Calculus using Mathematica
.nb Edition
Advanced Calculus using Mathematica: NoteBook Edition is a complete text on calculus of several variables written in Mathematica NoteBooks. The eText has large movable figures and interactive programs to illustrate things like “zooming in” to see “local linearity.” In addition to lots of traditional style exercises, the eText also has sections on computing with Mathematica. Solutions to many exercises are in closed cells of the eText. We use the text in a basic multivariable calculus course and a more advanced second course described in the syllabi below.
You need a copy of Mathematica to use the text. Many schools have site licenses that allow students to get Mathematica free.
Chapter 0: An Introduction to Mathematica & Calculus
Chapter 1: Basic Equations and Graphs
Chapter 2: Vector Geometry
Chapter 3: Derivatives and Graphs of Explicit Functions
Chapter 4: Implicit Curves, Surfaces, and Contour Plots
Chapter 5: Inverse and Implicit Functions
Chapter 6: Taylor’s Formula in Several Variables
Chapter 7: Max-min in Several Variables
Chapter 8: Multiple Integrals in Cartesian Coordinates
Chapter 9: Parametric Curves
Chapter 10: Motion along Curves: Gas, Brakes, & Tires
Chapter 11: Vector Fields and Velocity Flows in 2D
Chapter 12: Green’s Theorem, 2-D Divergence and Swirl
Chapter 13: Coordinate Systems in 2 Dimensions
Chapter 14: Path Integrals & Vector Fields in 3D
Chapter 15: Parametric Surfaces
Chapter 16: Curvature of Surfaces
Chapter 17: Coordinate Systems in 3 Dimensions
Chapter 18: Differential Forms
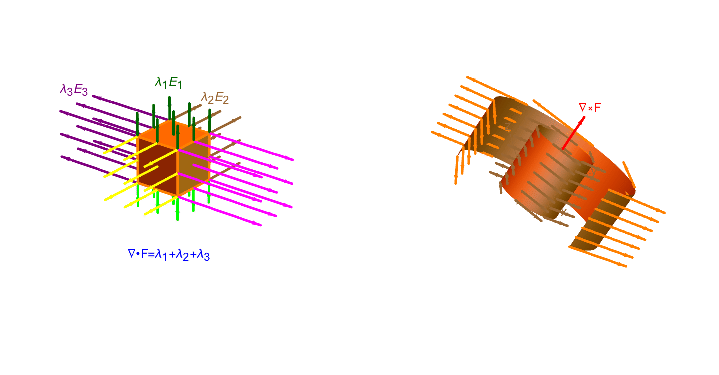
Chapter 19: Flow in 3D, Divergence & Curl
Chapter 20: Partial Differential Equations
Chapter 21: Infinite Series
Sample Syllabi
We have used these materials in second semester Engineering Mathematics 2: Multivariable Calculus for many years. Engineering Math 1 is essentially the content of Advanced Placement AB Calculus, so many students take Engineering Math 2 during their first semester. Click for sample Basic Syllabus. This syllabus is for a lecture/discussion course with hundreds of students.
The Engineering Math 2 course includes many topics from both the old “calc 2” and “calc 3.” One thing that may be special to our course is the inclusion of infinite series at the end of the course on “multivariable calculus.” This was a topic that the engineering faculty felt was needed after the second semester. To make time for this topic, we had to restrict vector field theory to 2D or Green’s Theorem, but we treat both the divergence and 2D curl version, so the students learn these ideas of “Div, Grad, Curl” in a basic 2D setting.
We also use these materials for a more advanced Engineering Math 5: Vector Calculus that only some engineering majors take. It is a “souped up” “calc 3.” These students have a brief matrix algebra course before the advanced course, so have some familiarity with eigenvalues and other matirx topics the old “calc 3” could not rely upon. We extend this by having them use Mathematica to compute matrix topics such as eigenvalues in MAX-min for large matrices. Click for a sample 2nd course syllabus. This is a smaller 3 hour course that allows us to assign a few small “projects” included in these materials. The one dimensional heat equation is a “road map” project used to add specifics to the general ideas in the heat and Laplace equations that follow from vector calculus. Moments of inertia are important in engineering and we have students actually make physical objects to go with that project.
Many topics such as Theorem 5.5.3 are included for instructors like our graduate TAs and a few exceptionally bright students who take the course. Topics like Functional Dependence and finding a Vector Potential of a divergence free vector field aren’t included in most advanced calculus books these days and Mathematica offers students the opportunity to compute such things easily. Perhaps the eText will contimue to be a useful reference after students finish the course.
Instructors can eMail Keith-Stroyan@uIOWA.edu for extra material like solutions to the labs and old exams.
Calculus: The Language of Change
Calculus is one of the great achievements of the human intellect. It has served as the language of change in the development of scientific thought for more than three centuries. Many problems in math, science, engineering, and other subjects involve the change in output as many inputs vary and this book deals with computation of "continuous" change caused by multiple changing inputs. The geometry and algebra of curves and surfaces in 3D is a concrete, useful, and beautiful way to understand many of the concepts, so that is one emphasis of these materials.
Modern computing helps make the subject even more concrete and can help with fast accurate calculations. I beleive that courses that incorporate modern computing can train future scientists to be better users of mathematics. I hope Advanced Calculus using Mathematica takes a step in that direction.
Best wishes in learning this wonderful and useful subject.