Many models used in categorical data analysis can be viewed as
special cases of generalized linear models. One example is the
Bradley-Terry model for paired comparisons. The Bradley-Terry model
deals with a situation in which n individuals or items are compared
to one another in paired contests. The model assumes there are
positive quantities 
, which can be assumed
to sum to one, such that
If the competitions are assumed to be mutually independent, then the
probability 
satisfies the logit
model
with 
. This model can be fit to a particular
set of data by setting up an appropriate design matrix and response
vector for a binomial regression model. For a single data set this can
be done from scratch. Alternatively, it is possible to construct
functions or prototypes that allow the data to be specified in a more
convenient form. Furthermore, there are certain specific questions
that can be asked for a Bradley-Terry model, such as what is the
estimated value of 
? In the object-oriented
framework, it is very natural to attach methods for answering such
questions to individual models or to a model prototype.
To illustrate these ideas, we can fit a Bradley-Terry model to the results for the eastern division of the American league for the 1987 baseball season [1]. Table 2 gives the results of the games within this division.
Table 2: Results of 1987 Season for American League Baseball Teams
The simplest way to enter this data is as a list, working through the table one row at a time:
(def wins-losses '( - 7 9 7 7 9 11
6 - 7 5 11 9 9
4 6 - 7 7 8 12
6 8 6 - 6 7 10
6 2 6 7 - 7 12
4 4 5 6 6 - 6
2 4 1 3 1 7 -))
The choice of the symbol - for the diagonal entries is
arbitrary; any other Lisp item could be used. The team names will also
be useful as labels:
(def teams '("Milwaukee" "Detroit" "Toronto" "New York"
"Boston" "Cleveland" "Baltimore"))
To set up a model, we need to extract the wins and losses from the wins-losses list. The expression
(let ((i (iseq 1 6))) (def low-i (apply #'append (+ (* 7 i) (mapcar #'iseq i)))))constructs a list of the indices of the elements in the lower triangle:
> low-i (7 14 15 21 22 23 28 29 30 31 35 36 37 38 39 42 43 44 45 46 47)The wins can now be extracted from the wins-losses list using
> (select wins-losses low-i) (6 4 6 6 8 6 6 2 6 7 4 4 5 6 6 2 4 1 3 1 7)Since we need to extract the lower triangle from a number of lists, we can define a function to do this as
(defun lower (x) (select x low-i))Using this function, we can calculate the wins and save them in a variable wins:
(def wins (lower wins-losses))
To extract the losses, we need to form the list of the entries for the transpose of our table. The function split-list can be used to return a list of lists of the contents of the rows of the original table. The transpose function transposes this list of lists, and the append function can be applied to the result to combine the lists of lists for the transpose into a single list:
(def losses-wins (apply #'append (transpose (split-list wins-losses 7))))The losses are then obtained by
(def losses (lower losses-wins))Either wins or losses can be used as the response for a binomial model, with the trials given by
(+ wins losses)
When fitting the Bradley-Terry model as a binomial regression model with a logit link, the model has no intercept and the columns of the design matrix are the differences of the row and column indicators for the table of results. Since the rows of this matrix sum to zero if all row and column levels are used, we can delete one of the levels, say the first one. Lists of row and column indicators are set up by the expressions
(def rows (mapcar #'lower (indicators (repeat (iseq 7) (repeat 7 7))))) (def cols (mapcar #'lower (indicators (repeat (iseq 7) 7))))The function indicators drops the first level in constructing its indicators. The function mapcar applies lower to each element of the indicators list and returns a list of the results. Using these two variables, the expression
(- rows cols)constructs a list of the columns of the design matrix.
We can now construct a model object for this data set:
> (def wl (binomialreg-model (- rows cols)
wins
(+ wins losses)
:intercept nil
:predictor-names (rest teams)))
Iteration 1: deviance = 16.1873
Iteration 2: deviance = 15.7371
Weighted Least Squares Estimates:
Detroit -0.144948 (0.311056)
Toronto -0.286871 (0.310207)
New York -0.333738 (0.310126)
Boston -0.473658 (0.310452)
Cleveland -0.897502 (0.316504)
Baltimore -1.58134 (0.342819)
Scale taken as: 1
Deviance: 15.7365
Number of cases: 21
Degrees of freedom: 15
To fit to a Bradley-Terry model to other data sets, we can repeat this process. As an alternative, we can incorporate the steps used here into a function:
(defun bradley-terry-model (counts &key labels)
(let* ((n (round (sqrt (length counts))))
(i (iseq 1 (- n 1)))
(low-i (apply #'append (+ (* n i) (mapcar #'iseq i))))
(p-names (if labels
(rest labels)
(level-names (iseq n) :prefix "Choice"))))
(labels ((tr (x)
(apply #'append (transpose (split-list (coerce x 'list) n))))
(lower (x) (select x low-i))
(low-indicators (x) (mapcar #'lower (indicators x))))
(let ((wins (lower counts))
(losses (lower (tr counts)))
(rows (low-indicators (repeat (iseq n) (repeat n n))))
(cols (low-indicators (repeat (iseq n) n))))
(binomialreg-model (- rows cols)
wins
(+ wins losses)
:intercept nil
:predictor-names p-names)))))
This function defines the function lower as a local function.
The local function tr calculates the list of the elements in
the transposed table, and the function low-indicators produces
indicators for the lower triangular portion of a categorical variable.
The bradley-terry-model function allows the labels for the
contestants to be specified as a keyword argument. If this argument is
omitted, reasonable default labels are constructed. Using this
function, we can construct our model object as
(def wl (bradley-terry-model wins-losses :labels teams))
The definition of this function could be improved to allow some of the keyword arguments accepted by binomialreg-model.
Using the fit model object, we can estimate the probability of Boston
defeating New York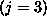 
:
> (let* ((phi (cons 0 (send wl :coef-estimates)))
(exp-logit (exp (- (select phi 3) (select phi 4)))))
(/ exp-logit (+ 1 exp-logit)))
0.534923
To be able to easily calculate such an estimate for any pairing, we can
give our model object a method for the :success-prob message
that takes two indices as arguments:
(defmeth wl :success-prob (i j)
(let* ((phi (cons 0 (send self :coef-estimates)))
(exp-logit (exp (- (select phi i) (select phi j)))))
(/ exp-logit (+ 1 exp-logit))))
Then
> (send wl :success-prob 4 3) 0.465077
If we want this method to be available for other data sets, we can construct a Bradley-Terry model prototype by
(defproto bradley-terry-proto () () binomialreg-proto)and add the :success-prob method to this prototype:
(defmeth bradley-terry-proto :success-prob (i j)
(let* ((phi (cons 0 (send self :coef-estimates)))
(exp-logit (exp (- (select phi i) (select phi j)))))
(/ exp-logit (+ 1 exp-logit))))
If we modify the bradley-terry-model function to use this prototype
by defining the function as
(defun bradley-terry-model (counts &key labels)
(let* ((n (round (sqrt (length counts))))
(i (iseq 1 (- n 1)))
(low-i (apply #'append (+ (* n i) (mapcar #'iseq i))))
(p-names (if labels
(rest labels)
(level-names (iseq n) :prefix "Choice"))))
(labels ((tr (x)
(apply #'append (transpose (split-list (coerce x 'list) n))))
(lower (x) (select x low-i))
(low-indicators (x) (mapcar #'lower (indicators x))))
(let ((wins (lower counts))
(losses (lower (tr counts)))
(rows (low-indicators (repeat (iseq n) (repeat n n))))
(cols (low-indicators (repeat (iseq n) n))))
(send bradley-terry-proto :new
:x (- rows cols)
:y wins
:trials (+ wins losses)
:intercept nil
:predictor-names p-names)))))
then the :success-prob metod is available immediately for a
model constructed using this function:
> (def wl (bradley-terry-model wins-losses :labels teams)) Iteration 1: deviance = 16.1873 Iteration 2: deviance = 15.7371 ... > (send wl :success-prob 4 3) 0.465077
The :success-prob method can be improved in a number of ways. As one example, we might want to be able to obtain standard errors in addition to estimates. A convenient way to provide for this possibility is to have our method take an optional argument. If this argument is nil, the default, then the method just returns the estimate. If the argument is not nil, then the method returns a list of the estimate and its standard error.
To calculate the standard error, it is easier to start with the logit of the probability, since the logit is a linear function of the model coefficients. The method defined as
(defmeth bradley-terry-proto :success-logit (i j &optional stdev)
(let ((coefs (send self :coef-estimates)))
(flet ((lincomb (i j)
(let ((v (repeat 0 (length coefs))))
(if (/= 0 i) (setf (select v (- i 1)) 1))
(if (/= 0 j) (setf (select v (- j 1)) -1))
v)))
(let* ((v (lincomb i j))
(logit (inner-product v coefs))
(var (if stdev (matmult v (send self :xtxinv) v))))
(if stdev (list logit (sqrt var)) logit)))))
returns the estimate or a list of the estimate and approximate
standard error of the logit:
> (send wl :success-logit 4 3) -0.13992 > (send wl :success-logit 4 3 t) (-0.13992 0.305583)The logit is calculated as a linear combination of the coefficients; a list representing the linear combination vector is constructed by the local function lincomb.
Standard errors for success probabilities can be computed form the results of :success-logit using the delta method:
(defmeth bradley-terry-proto :success-prob (i j &optional stdev)
(let* ((success-logit (send self :success-logit i j stdev))
(exp-logit (exp (if stdev (first success-logit) success-logit)))
(p (/ exp-logit (+ 1 exp-logit)))
(s (if stdev (* p (- 1 p) (second success-logit)))))
(if stdev (list p s) p)))
For our example, the results are
> (send wl :success-prob 4 3) 0.465077 > (send wl :success-prob 4 3 t) (0.465077 0.0760231)
These methods can be improved further by allowing them to accept sequences of indices instead of only individual indices.