The basic high school functions defined by explicit formulas are:
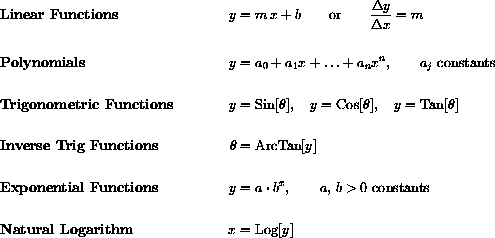
Note: Natural log is sometimes denoted ln y) in high school texts, where log y) denotes the base 10 log. We do not need base 10 logs.
All of these functions are reviewed in this chapter.
28.1
The slope-intercept formula for a linear function,
The exercises in Chapter 1 of the main text on linear functions are important building blocks for calculus.
You should work them even if your high school math skills are sharp.
An advanced topic on linear functional identities is studied in the Math Background material on CD and in the Project book.
The scientific project on CO2 uses linear functions to try to predict the increase of "greenhouse gases."
28.2
Polynomials are functions of the form
Many basic geometrical formulas are single-term polynomials (monomials), for example,
Check your work with the computer using the Polynomials program from the High School Review Folder in the courseware for either Mathematicaor Maple.
28.3
The area of a rectangle is a function of its length and width
Example CD-28.1
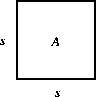
The area of a Square is a Function of the Length of its Side
In homework problems involving applications, we want you to
(1) Explicitly list your variables with units and sketch a figure if appropriate.
(2) Translate the information stated in the problem into formulas in your variables. (If this translation is difficult, you may not have chosen the best variables.) Often, it is helpful to balance units on both sides of an equation.
(3) Formulate the question in terms of your variables and solve.
(4) Explicitly interpret your solution.
Be sure to restate the question in terms of your variables.
We will say more about this as the exercises become more difficult.
Example CD-28.2
Express the Circumference of a Circle as a Function of its Area.
Solution:Step 1: We use the following variables:
Step 2: We know the formulas for circumference and area of a circle:
Step 3: The question asks us to find circumference as a function of area as the independent variable: Find C=C[A]. Notice that we have introduced an extra variable, the radius r, to help us solve the problem.
Begin by solving the area equation for r:
Notice that the circumference function is not a polynomial because it involves a square root.
Square roots are special power functions studied in the next section.
28.4
Power functions are functions of the form
The formula for the surface area of a cube as a function of its volume may be written
You can check your work on these exercises with the program ExpRules in the Chapter 28 folder.
28.5
In a right triangle with acute angle
Example CD-28.3
Derive the Functional Equation
The Pythagorean Theorem says
Section CD-28.9 reviews identities beyond the basic trig identities.
Besides SOH-CAH-TOA, there are just three main identities that you must know.
You do need to remember how to use these three, and the background review should help if you are rusty on that.
The Mathematical Background chapter on Functional Identities studies identities more abstractly.
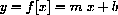
expresses the "output" as the variable y in terms of the "input" variable x. In this case, y is the dependent variable, and x is the independent variable.
The letters m and b are "parameters" that stand for constants (that do not change as x varies). All values of x are permitted as input, so the "domain" of this function consists of all real numbers.
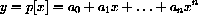
sums of constants
 times integer powers of the independent variable x. For example,
times integer powers of the independent variable x. For example,
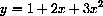
In this case, the independent variable is x, the dependent variable is y, and the letters
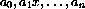 , and n are parameters.
The parameters do not change as x varies.
Again, the domain consists of all real values of x.
, and n are parameters.
The parameters do not change as x varies.
Again, the domain consists of all real values of x.



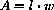
In this case, area is a function of two independent variables
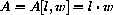
where the "domains" or permissible input values of l and w satisfy

A is a function of l and w in that once their values are specified, then A is determined.
For example, if
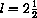 and
and
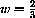 , then
, then
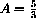 .
.
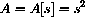
with domain
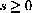
A is a function of a single independent variable.
The formula A=s2 makes perfectly good mathematical sense when s is negative, but the geometrical meaning as length does not.
Geometrically, the function A=A[s] has a domain restricted to
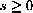 .
.
Procedure
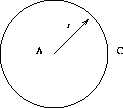
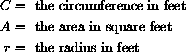
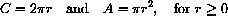
This translation step just translates implicit knowledge of circles.
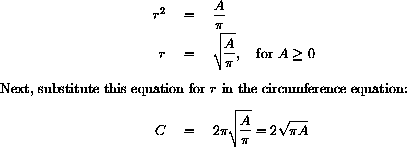
This gives the solution
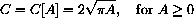
Step 4: The interpretation of the solution is simply that this formula gives circumference as a function of area.
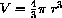 and the surface area in terms of radius is
and the surface area in terms of radius is
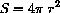 .)
.)
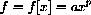
for constants a and p. The formula for the circumference of a circle in terms of its area (derived in the previous section) can be expressed as a power,
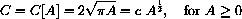
where c is the constant
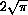 . In this case, the domain of the function consists of only positive values of the independent variable A, because zero areas do not make sense.
The formula does make sense with A=0, but even the formula is not real valued if A is negative. (It can be given as a complex number, of course.)
. In this case, the domain of the function consists of only positive values of the independent variable A, because zero areas do not make sense.
The formula does make sense with A=0, but even the formula is not real valued if A is negative. (It can be given as a complex number, of course.)

because A=6s2 and V=s3, where s is the length of the cube's edge, so
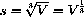 and substituting we obtain
and substituting we obtain
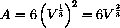
You may need to brush up on rules of exponents from high school.
You need to be proficient at the use of these rules in order to take advantage of the powerful symbolics in calculus.
28.4.1

for example,
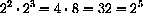 ,
, 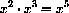 .
.
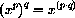
for example,
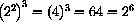 ,
, 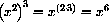 .
.
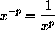
for example,
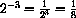 ,
, 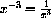 .
.
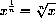
for example,
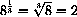 ,
, 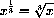 .
.
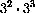
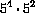
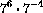
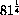
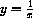

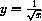


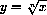
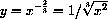 , etc...
, etc...
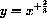
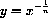
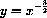
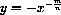
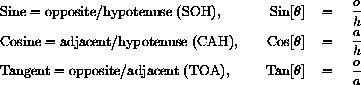
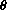 as shown and with sides of lengths o opposite
as shown and with sides of lengths o opposite
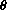 , a adjacent to
, a adjacent to
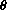 and hypotenuse h, we have
and hypotenuse h, we have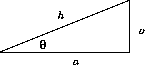
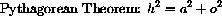
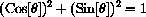
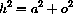
SOH-CAH-TOA gives
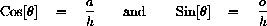
If we divide the Pythagorean identity by h2 we have

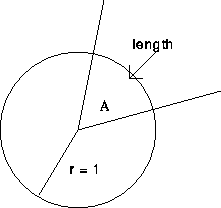
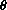 , the radian measure.
The (x,y) coordinates of the point on the unit circle where the side of the angle crosses are
, the radian measure.
The (x,y) coordinates of the point on the unit circle where the side of the angle crosses are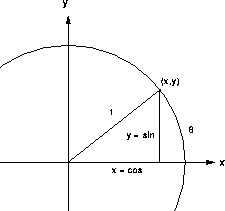
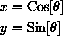
We have
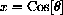 and
and
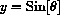 because the hypotenuse of the triangle is the unit radius of the circle.
Using SOH-CAH-TOA,
because the hypotenuse of the triangle is the unit radius of the circle.
Using SOH-CAH-TOA, 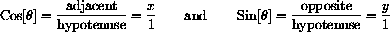
These equations can even be taken as the "definition" of sine and cosine because this SOH-CAH-TOA argument can be reversed if we start from the unit hypotenuse and extend to a larger triangle.
 ,
,  ,
,  ,
, 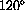 .
.
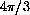 ,
, 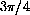 ,
, 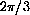 ,
, 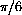 ,
, 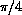 , 1.
, 1.
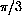 units counterclockwise along the unit circle measured from (1,0).
The line L makes an angle of
units counterclockwise along the unit circle measured from (1,0).
The line L makes an angle of
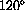 with the positive x axis, measured counterclockwise.
Find the radian measure of this angle.
Find the (x,y)-point in the second quadrant where the line L crosses the unit circle.
with the positive x axis, measured counterclockwise.
Find the radian measure of this angle.
Find the (x,y)-point in the second quadrant where the line L crosses the unit circle.
Draw a unit circle and an angle with radian measure
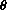 measured counterclockwise from the x-axis.
Draw the negative angle
measured counterclockwise from the x-axis.
Draw the negative angle
 measured clockwise.
Observe that the point where the angle crosses the unit circle lies vertically above the point where the negative angle crosses, so the components of the point for the negative angle are (x,-y) when the components for the positive angle are (x,y).
Prove that cosine is an even function,
measured clockwise.
Observe that the point where the angle crosses the unit circle lies vertically above the point where the negative angle crosses, so the components of the point for the negative angle are (x,-y) when the components for the positive angle are (x,y).
Prove that cosine is an even function,
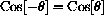 and that sine is an odd function,
and that sine is an odd function,
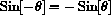 .
.
Problem CD-28.1
Describe the motion of the piston shown in Figure CD-28.3 when the crankshaft turns 2000 revolutions per minute.
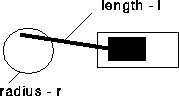
Figure CD-28.3: Crank and piston
28.6
The last major kinds of function that you studied in high school are logarithms and the inverse, exponential functions.
We will study these more carefully during the course, because different high schools treat these functions so differently.
This section shows you one application of exponential functions that hinges on the functional identity
Notice the difference between an exponential function
Because the widespread use of inexpensive calculators, base 10 logs are no longer of much interest.
Natural base or base "e" logs and exponentials are still very important, as we will see throughout the course.
The fundamental functions' names are
Of course, it still makes perfectly good sense to use other bases, particularly for exponentials.
However, calculus becomes much simpler when logs and exponentials are expressed in the "natural" base e. The following example uses base 2 and an exercise in Chapter 8 asks you to express this base 2 function in terms of base e. The reexpression does not seem advantageous now, but it will be once we have calculus, because the derivative
Use a calculator or the program LogGth to compute the natural logs in the next exercise.
Properties of exponents play an important role in exponential functions.
Let's return to the number of mold cells in my basement
Use the program ExpGth in the High School Review folder for help with the algae growth computations in the next problem.
Problem CD-28.2
Growth of Algae
28.7
Explicit formulas in science can be complicated.
For example, Planck's Radiation Law (described in a Chapter of the Scientific Projects) can be written
Symbolic calculus first gives rules for the basic kinds of functions and then gives rules for functions built up from basic functions by sums, products, and compositions.
In order to understand the rules of calculus, you need to be familiar with function notation for high school functions.
We can think of this in terms of a function, y=f[x]=ex, replacing the input x with the expression
You should also be familiar with the function notation for chains.
If
Example CD-28.4
The Expression
In Chapter 1 of the main text we used the expression above to compute the slope of a secant line.
Let's break down the meaning of this notation in the case
The expression
Finally, the expression
if
Note that
if
The program Functions contains part of the solution to these exercises.
We can substitute symbolic expressions in Mathematicaand Maplefunctions and make compositions.
Problem CD-28.3
Compute f[x+1] (it will also be a piecewise defined function).
28.8
Parameters play an important role in the solution of many scientific problems, where parameters are often measured physical constants.
We may find how a maximum oscillation depends on a mass.
Specific solutions for known masses do not yield the same scientific insights as the formula with a parameter.
So, what are parameters mathematically? One book "defined" parameter as "a variable that is constant." That "definition" is a contradiction in terms and yet suggests the spirit in which parameters are often used.
In the slope-intercept formula
In short, a parameter is another letter or unknown in our formulas.
Roughly speaking, it is called a parameter if it is treated as an unknown constant as far as the independent variables are concerned.
We will ask you to work with parameters often.
If the extra letters confuse you in a problem, choose a special case or two and work through the problem with specific numbers instead of parameters.
Then, generalize your work to a letter instead of your specific numbers.
The next problem is easy once you understand the geometric meaning of the algebra.
This is what we want you to learn (or review). You can check your work with the program SlideSquash.
Problem CD-28.4
Animation of Parameters
1) Let
2) Let
3) Let
4) Can every quadratic of the form
5) Verify your work using the program SlideSquash from the Chapter 28 folder.
The first animation there corresponds to part (1) above but plots 41 graphs for
28.9
All of the identities you need to recall from high school are
Double-angle formulas are special cases of the addition formulas.
Take
Example CD-28.5
Conversion of Base
Here is the way to convert bx to the natural base.
Solve
For example, if b=3, then
The natural base logs and exponentials are important in calculus.
The reason they are called "natural" is because they have the simplest derivatives, whereas other bases have a "less natural" calculus.
This is why we convert to base e.
Example CD-28.6
Compound Interest
Compound interest on money is given by an exponential function.
If you invest a "principal" P for a time t (in years) at the annual rate r (as a decimal), compounded n times per year, then your balance is
Quarterly compounded interest at a 10% annual rate for one year would give
Example CD-28.7
Double Your Money
Logarithms enter finances when you wish to answer questions such as "How long does it take to double an investment at 10% quarterly compounded interest?" We want our balance B to equal 2P after an unknown time t,
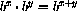 . Functional equations such as this are very important.
In this case the identity is closely related to a differential equation describing growth.
Again, the Mathematical Background Chapter on Functional Identities contains additional information on general identities, but this particular case can be understood intuitively in terms of growth of algae.
. Functional equations such as this are very important.
In this case the identity is closely related to a differential equation describing growth.
Again, the Mathematical Background Chapter on Functional Identities contains additional information on general identities, but this particular case can be understood intuitively in terms of growth of algae.

and a power function


and the inverse
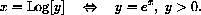
Note that some books use ln[y] for the natural logarithm, and a few still use log [y] for base 10 logarithm.
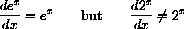
A super duper computer can add ten billion terms of the form 1+1/2+1/3+1/4+1/5+... per second with perfect accuracy.
The size of the sum 1+1/2+...+1/n is approximately
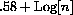 . How many centuries would it take this computer to add enough terms to get a sum over 100?
. How many centuries would it take this computer to add enough terms to get a sum over 100?
28.6.1
Suppose the mold in my basement doubles the number of cells every hour.
At midnight, there are 56 cells.
At 1:00 am, there are
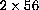 cells.
At 2:00 am, there are
cells.
At 2:00 am, there are
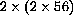 cells and
cells and
 . At 3:00 am there are
. At 3:00 am there are
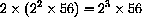 cells.
You can see that at integer hours,
cells.
You can see that at integer hours,
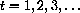 , there are
, there are
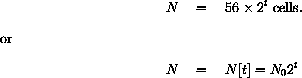
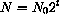
How many mold cells should there be in
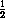 hour? If we substitute
hour? If we substitute
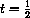 , the answer is
, the answer is
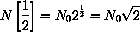
Is this right? If so, how many in the next half hour? We should use the same rule, so

Rules of exponents say that this agrees with the integer formula
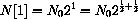
On a warm summer day with plenty of nutrients, supplied by runoff, the number of algae cells in a formerly clear pond doubles every 6 hours.
This is the time it takes a cell to divide; but, naturally, the cells do not all divide simultaneously, so a population of many cells grows almost continuously with time.
Suppose you begin with N0 cells at elapsed time 0. Express the number of cells as a function of time in hours.
How many cells are there after 3 hours? What do fractional values of N mean? How many are there after 1 day? How many in 1 week? If one cell has mass 1 mg. and we start with 1000 cells, what is the mass of the algae cells after 1 month? What is the approximate mass of all the water in Lake Michigan in these units? Suppose the lake fills at time tf. How much algae is there 6 hours later? Can algae continue to double every six hours?

for constants a and b. This expresses the intensity I of radiation at (angular) frequency
 for a body at absolute temperature T. The specific details are not important yet.
We want to point out that I is built up using addition, multiplication, and division from a polynomial power formula
for a body at absolute temperature T. The specific details are not important yet.
We want to point out that I is built up using addition, multiplication, and division from a polynomial power formula
substituting
 for x, subtracting 1, multiplying, and dividing.
When T is fixed, we want to use symbolic formulas of calculus to find
for x, subtracting 1, multiplying, and dividing.
When T is fixed, we want to use symbolic formulas of calculus to find
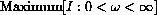 . (The maximum is called Wien's Law of radiation.) By the end of the semester, you will think of Planck's formula as a straightforward combination of simple functions. (The way Planck found the formula is not simple.
He got a Nobel Prize for the connection with science.)
. (The maximum is called Wien's Law of radiation.) By the end of the semester, you will think of Planck's formula as a straightforward combination of simple functions. (The way Planck found the formula is not simple.
He got a Nobel Prize for the connection with science.)
28.7.1
In Planck's formula, we substitute
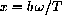 into the natural exponential function.
In old-fashioned notation, we might write
into the natural exponential function.
In old-fashioned notation, we might write
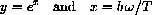
In a computer program, if we first entered both expressions and then asked for the symbolic value of y, we would get the answer,
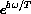 . Linking variables together in a chain like this is an important symbolic construction.
. Linking variables together in a chain like this is an important symbolic construction.
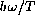 ,
, 
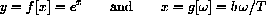
then the substitution of variables is the function

This notation is useful in some contexts.
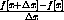

This function rule means "Take any input value x and cube it." We could express this by leaving a blank space,
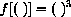
When we put x in the blank space, we get x3. If we put the expression
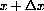 into the blank space, we get
into the blank space, we get
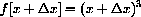
 is obtained by subtraction of the two results,
is obtained by subtraction of the two results,
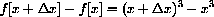
This expression can be expanded, but that is another matter.

Expansion and simplification of this expression gives
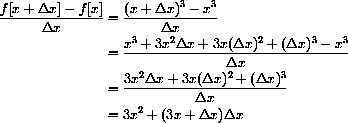
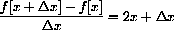

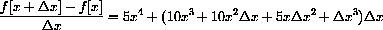
Show that
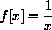 , then
, then
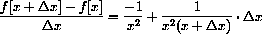
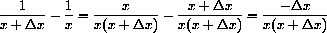 and that
and that
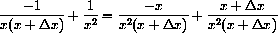
Show that
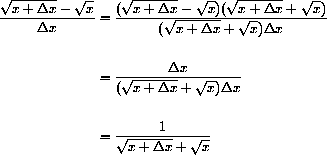
and that
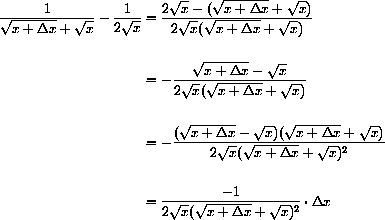
Conclude that
 , then
, then
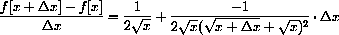
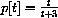 . Write a single expression for:
. Write a single expression for:
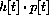
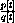
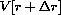
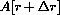
Let
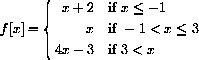
Compute f[-1], f[3]. Compute other values of f[x] and sketch the graph of f[x]. The graph consists of separate "pieces," and f[x] is called a "piecewise-defined" function.
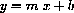
we "hold m and b fixed" while we vary x. Only varying x gives a single, straight-line graph.
We can also plot a family of lines as we change a parameter.
Here are two examples.
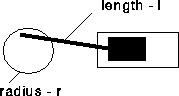
Figure CD-28.4: Variation of the b parameter in
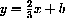

Figure CD-28.5: Variation of the m parameter in

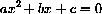
where a, b and c are parameters? (You learned the "quadratic formula" in high school.)
In high school, you learned that the graph of every quadratic polynomial is a parabola.
A geometrically convenient way to write the parameters is

for
 ,
,  ,
,  (unknown) constants.
(unknown) constants.
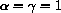 and plot the family of curves
and plot the family of curves
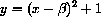
for
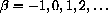 .
.
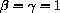 and plot the family of curves
and plot the family of curves
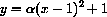
for
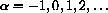 .
.
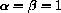 and plot the family of curves
and plot the family of curves

for
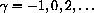 .
.
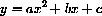
also be written in the form
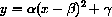
and vice versa? Why? What are the restrictions on a and
 ?
?
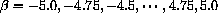
The animation uses the graphs to make a computer "movie" of the graph sliding across the screen.
The parts of the program left for you to work correspond to parts (2) and (3) above.
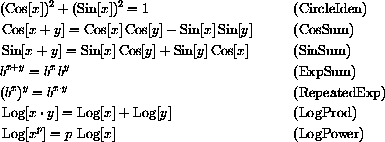
but you must be able to use these identities.
Some practice exercises using these basic identities are given in the next two sections.
28.9.1
The seven identities above can be used to find other identities.
For example, to prove that

we need to use the (CircleIden), 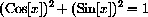 and the relationship between the trig functions,
and the relationship between the trig functions,
 and
and
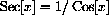 . Simply divide the basic identity by
. Simply divide the basic identity by
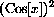 ,
, 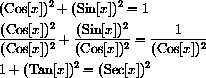

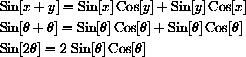
Half-angle formulas can be found by a similar change of variables,
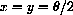 .
.
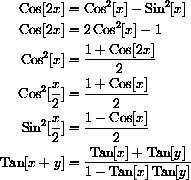
28.9.2
In addition to the four high school identities,
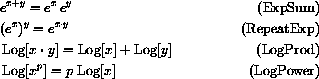
you need to remember that the natural log and exponential are inverse functions, that is,
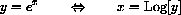
We may write the inverse relationship more operationally as
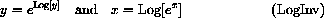
Using Log we can convert any other base bx to an expression in base e as follows:
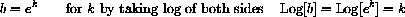
The Law of Repeated Exponents gives,
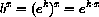
for this value of the constant k.
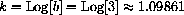 and
and
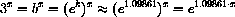
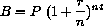
For example, suppose you invest
$500 at 10% (r = 0.1) compounded each 1/2 year.
In six months your balance is
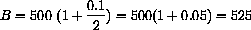
If this amount all now earns interest, after six more months, you have
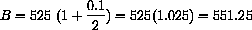
This is two compoundings in a year,
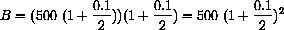
Notice that this gives
$1.25 more interest than simple interest for a year, because the six month interest earned interest for the second half of the year.
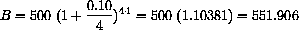
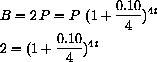
Take the log of both sides and use the (LogPower) identity to solve for t, 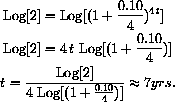
Simple noncompounded interest at 10% would take 10 years to double, whereas it takes only 7 years with compound interest.
In 10 years compounded quarterly, we have 2.685 times our original investment.
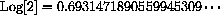 . Express the function f[x]=2x in terms of the natural base exponential e=2.7182818284590452356028747..., f[x]=2x=e??
. Express the function f[x]=2x in terms of the natural base exponential e=2.7182818284590452356028747..., f[x]=2x=e??
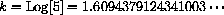 . Express the function f[x]=ex+k in the form
. Express the function f[x]=ex+k in the form
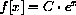 for some constant C. (HINT: Use the (ExpSum) identity.)
for some constant C. (HINT: Use the (ExpSum) identity.)
How long would it take at 10% interest compounded monthly to triple your investment? 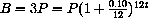 Solve for t.
Solve for t.
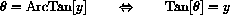
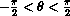 . For example, if o is fixed at 7.5, then
. For example, if o is fixed at 7.5, then
 as a function of a is
as a function of a is

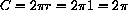 , the distance all the way around a unit circle is
, the distance all the way around a unit circle is
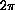 . The distance half way around, corresponding to an angle of
. The distance half way around, corresponding to an angle of
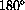 is
is
 . This simple relationship gives us a proportionality that we can use to convert degrees to radians or radians to degrees:
. This simple relationship gives us a proportionality that we can use to convert degrees to radians or radians to degrees: 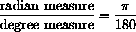
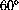 can be converted to radian measure by
can be converted to radian measure by

 .
.
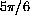 has its degree measure computed as follows:
has its degree measure computed as follows: 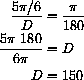
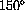 .
.