27.2
Recall the idea of the Fundamental Theorem of Integral Calculus: In order to find
The partial sum
Series we know can be used to estimate the error in series we do not know.
If we sum 100 terms of the series of terms
27.3
Example CD-27.1
Comparison of the Harmonic Series and Natural Log Integral
The continuous function
This shows that the harmonic series diverges.
Example CD-27.2
Integral Comparison for
An estimate of series with integrals can be used to prove convergence.
We know
Compare this to Exercise CD-27.2.2.
The idea of this section can be summarized as follows:
The two previous simple integral comparison exercises generalize as follows:
27.4
Example CD-27.3
We know from Exercise CD-27.3.4 above that 1+1/2p+...+1/np+... converges for any p>1. We also know from the rate of growth of log that
Example CD-27.4
We know from the rate of growth of log that
The harmonic series diverges and the tail of this series is larger,
When the limit of the ratio of the terms of two series are non-zero, they represent the same "order of infinitesimal" and thus converge or diverge together.
We can also use each new numerical series in function estimates.
For example, the Fourier series
27.5
The series
The projects on series show you the simple formula for Fourier coefficients and give the interesting convergence theorem for functions.
Fourier series can converge delicately.
For example, the identity
Section Summary
A series of the form
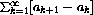 collapses like a telescope.
collapses like a telescope.
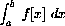
we first find an antiderivative, F[x] such that its differential satisfies dF[x]=f[x]dx. The increment equation for this new function says
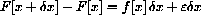
so, the defining sum for the integral collapses or "telescopes,"
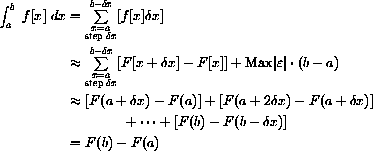
Sometimes, we can use this idea to find the sum of an infinite series.
We cannot antidifferentiate, but we can occasionally find a difference,

because
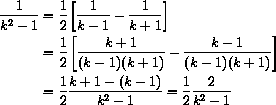

Find the sum of the series
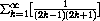
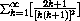
How fast does the series
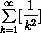
converge? Use the estimates
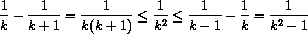
and sum the telescoping terms.
The error series satisfies
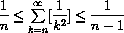
How much is the difference between these estimates of error? This difference gives us
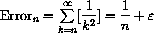
with
 no more than
no more than
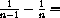 ???
???
 , how much is the error? How does the error compare with the next term,
, how much is the error? How does the error compare with the next term,
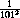 ?
?
Section Summary
A way to estimate series above or below is to compare them with integrals.
 decreases, so it stays below
decreases, so it stays below
 for
for
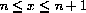 . This means that one term of the series
. This means that one term of the series
 satisfies
satisfies

and
Figure CD-27.1 shows this estimate graphically.
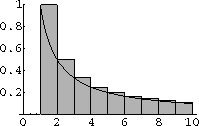
Figure CD-27.1: An integral below
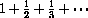
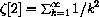
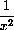 is decreasing, so we have
is decreasing, so we have
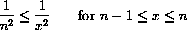
This makes
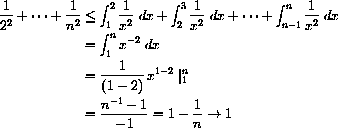
In fact, the error for the series satisfies

Figure CD-27.2 shows this estimate graphically.
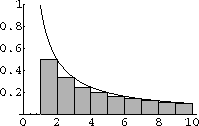
Figure CD-27.2: An integral above

Theorem CD-27.1
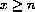 . The series of positive decreasing terms, ak=f(k),
. The series of positive decreasing terms, ak=f(k), 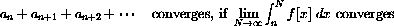
and
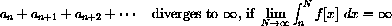
Test the following series for divergence by squeezing an integral below them:
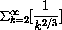
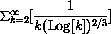
Test the following series for convergence by squashing them below an integral:
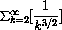
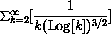
Show that the following series diverge if
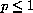 and converge if p>1:
and converge if p>1:

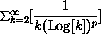
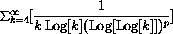
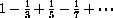 converges.
Why?
converges.
Why? 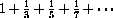 converge?
converge? Section Summary
Each time we learn a new convergent or divergent series, we can use it to compare to many other series.
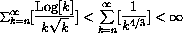
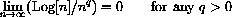
The series
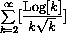
must therefore converge, because
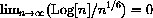 so that eventually
so that eventually
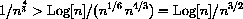
and, from that point on,
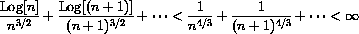
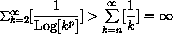
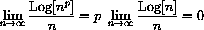
so, in particular, for sufficiently large n,  for
for
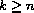 and
and
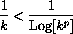
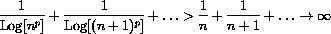
Theorem CD-27.2
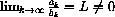 . Then
. Then
 converges, so does
converges, so does
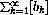 .
.
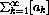 diverges, so does
diverges, so does
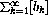 .
. 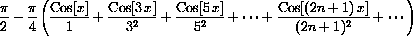
is convergent absolutely and uniformly because
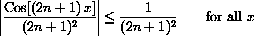
and 1+1/9+1/25+... converges.
Test the following series for convergence or divergence:
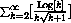
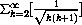

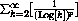
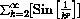
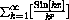
Section Summary
Fourier series arise in many mathematical and physical problems.
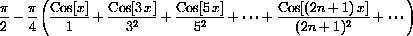
converges to the function that equals |x| for
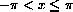 and is then repeated periodically.
Some approximating graphs are:
and is then repeated periodically.
Some approximating graphs are: 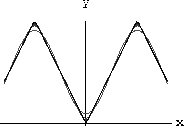
Figure CD-27.3: Fourier series for f[x]=|x| 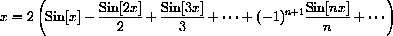
is a valid convergent series for
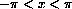 . However, the Weierstrass majorization does not yield a simple convergence estimate, because
. However, the Weierstrass majorization does not yield a simple convergence estimate, because
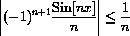
is a useless upper estimate by a divergent series.
This series converges but not uniformly, and its limit function is discontinuous because repeating x periodically produces a jump at
 as follows:
as follows: 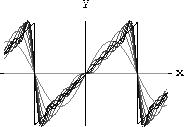
Figure CD-27.4: Fourier series for f[x]=x