Advanced Calculus using Mathematica

Advanced Calculus using Mathematica: NoteBook Edition is a complete text on calculus of several variables written in Mathematica NoteBooks.

Implicit 3D: Procedure 4.5.1

Procedure  4.5.1: Finding the Implicit Tangent Plane

Suppose f[x,y,z] is smooth in a neighborhood of a particular fixed X=X(x,y,z). To find the equation of the plane tangent to the implicit contour surface AdvCalcMathWeb_63.png at X=X(x,y,z), for AdvCalcMathWeb_64.pngconstant, do the following steps:

1.  Compute the general symbolic partial derivatives AdvCalcMathWeb_65.png, AdvCalcMathWeb_66.png, and AdvCalcMathWeb_67.png.  Verify that the formulas f[x,y,z], AdvCalcMathWeb_68.png, AdvCalcMathWeb_69.png, and AdvCalcMathWeb_70.png are valid in a box about our particular point of tangency, X(x,y,z) and write the symbolic total differential of the equation

AdvCalcMathWeb_71.png (the partials are functions)

The right hand side is zero since the partial derivatives of a constant AdvCalcMathWeb_72.png are zero.

2.  Calculate the specific values of the partial derivatives at the particular X(x,y,z), AdvCalcMathWeb_73.png, AdvCalcMathWeb_74.png, and AdvCalcMathWeb_75.png, verify that they are not all zero, and write the specific total differential at this point:

p·d x+q·d y+r·d z=0 or G• dX =0 (the coefficients are numbers)

3.  If you want the equation of the tangent plane in (x,y,z)-coordinates, say AdvCalcMathWeb_76.png is your particular point of tangency. The local  (d x,d y,d z)-coordinates are related to (x,y,z)-coordinates by AdvCalcMathWeb_77.png, AdvCalcMathWeb_78.png, AdvCalcMathWeb_79.png, so replace  d x,  d y, d z  with AdvCalcMathWeb_80.png, AdvCalcMathWeb_81.png, AdvCalcMathWeb_82.png obtaining the equation:

AdvCalcMathWeb_83.png

The result of Step 2 an implicit plane through the (d x, d y, d z)-origin with perpendicular ∇f[x,y,z].  You can plot the tangent plane using this equation in local coordinates  (d x, d y, d z) centered at the particular (x,y,z).  The equation says, “An unknown vector d X =(d x, d y, d z) (with origin at the point of tangency X(x,y,z)) lies on the tangent line provided it is perpendicular to the particular gradient G(p,q,r).”

The result of Step 3 is an implicit plane through the point AdvCalcMathWeb_84.png with perpendicular AdvCalcMathWeb_85.png.  This equation says, “An unknown vector X (with origin at (x,y,z)=(0,0,0)) lies on the tangent line provided its displacement from AdvCalcMathWeb_86.png is perpendicular to the particular gradient G(p,q,r).”  Notice that to correctly evaluate this final expression, you need to perform steps (1), (2), and (3) in that order.  

When G=0, the implicit equation does not define a plane.  In this case we may not have a tangent.  We take this up in Chapter 5 on The Implicit Function Theorem.  The rigorous justification for the procedure is the Implicit Function Theorem for one equation in 3 unknowns.

Example

Find the equation tangent to AdvCalcMathWeb_87.png at AdvCalcMathWeb_88.png

Solution

First, the function AdvCalcMathWeb_89.png is smooth at all (x,y,z) by the 3-variable extension of the Theorem on Smooth Formulas.

The general symbolic total differential of the equation is

AdvCalcMathWeb_90.png

At the particular point AdvCalcMathWeb_91.png, the differential is

AdvCalcMathWeb_92.png    ⇔  AdvCalcMathWeb_93.png

The plane through AdvCalcMathWeb_94.png perpendicular to AdvCalcMathWeb_95.png

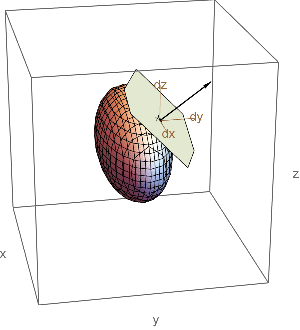
AdvCalcMathWeb_96.gif

Figure 4.5.3: The Plane Tangent to an Ellipsoid