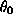Exercises

1. To be able to think about prior distributions for the two parameters in this problem we need to try to understand what the parameters represent. The parameter is fairly easy to understand: it is the mean survival time for patients with WBC = 10000. The parameter 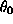is a little more difficult to think about. In represents the approximate percent difference in mean survival time for patients with WBC differing by one percent. Because of the minus sign in the mean relationship, and the expected inverse relation between WBC and mean survival time, 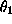is expected to be positive.

   Consider an informative prior distribution that assumes the two parameters a priori independent, takes to be normally distributed with mean 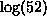and standard deviation 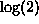, and 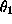to be exponentially distributed with mean . This prior is designed to represent an opinion that mean survival time at WBC = 10000 should be around one year, but that guess could easily be off by a factor of two either way. The percentage change in the mean for a one percent change in WBC should be on the order of one to ten or so. Examine the posterior distribution for this prior and compare your results to the results for the vague prior used above.

2. Construct and examine a posterior distribution for the parameters of the gamma model based on the aircraft data of Section 12.