Spinning Plots

  If we are interested in exploring the relationship among three variables then it is natural to imagine constructing a three dimensional scatterplot of the data. Of course we can only see a two dimensional projection of the plot on a computer screen -- any depth that you might be able to perceive by looking at a wire model of the data is lost. One approach to try to recover some of this depth perception is to rotate the points around some axis. The spin-plot   function allows you to construct a rotatable three dimensional plot.

As an example let's look a some data collected to examine the relationship between a phosphate absorption index and the amount of extractable iron and aluminum in a sediment (Devore and Peck [11, page 509, Example 6,]). The data can be entered with the expressions

 
(def iron (list 61 175 111 124 130 173 169 169 160 224 257 333 199))
(def aluminum (list 13 21 24 23 64 38 33 61 39 71 112 88 54)) 
(def absorption (list 4 18 14 18 26 26 21 30 28 36 65 62 40))

(spin-plot (list absorption iron aluminum))

  
Figure 7: Two views of a rotatable plot of data on iron content, aluminum content and phosphate absorption in sediment samples.

The argument to spin-plot is a list of three lists or vectors, representing the x, y and z variables. The z axis is initially pointing out of the screen. You can rotate the plot by pointing at one of the Pitch, Roll or Yaw squares and pressing the mouse button. By rotating the plot you can see that the points seem to fall close to a plane. The plot on the right of Figure 7 shows the data viewed along the plane. A linear model should describe this data quite well.

As a second example, with the data defined by

(def strength (list 14.7 48.0 25.6 10.0 16.0 16.8 20.7 38.8
                    16.9 27.0 16.0 24.9 7.3 12.8))
(def depth (list 8.9 36.6 36.8 6.1 6.9 6.9 7.3 8.4 6.5 8.0 4.5 9.9 2.9 2.0))
(def water (list 31.5 27.0 25.9 39.1 39.2 38.3 33.9 33.8
                 27.9 33.1 26.3 37.8 34.6 36.4))

(spin-plot (list water depth strength)
           :variable-labels (list "Water" "Depth" "Strength"))

  
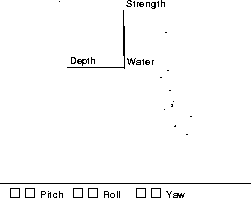
Figure 8: Rotatable plot of measurements on permafrost samples.

produces a plot that can be rotated to produce the view in Figure 8. These data concern samples of thawed permafrost soil. strength is the shear strength, and water is the percentage water content. depth is the depth at which the sample was taken. The plot shows that a linear model will not fit well. Devore and Peck [11] suggest fitting a model with quadratic terms to this data.

  The function spin-plot also accepts the additional keyword argument scale. If scale is T, the default, then the data are centered at the midranges of the three variables, and all three variables are scaled to fit the plot. If scale is NIL the data are assumed to be scaled between -1 and 1, and the plot is rotated about the origin. Thus if you want to center your plot at the means of the variables and scale all observations by the same amount you can use the expression

(spin-plot (list (/ (- water (mean water)) 20)
                 (/ (- depth (mean depth)) 20)
                 (/ (- strength (mean strength)) 20))
           :scale nil)

Rotation speed can be changed using the plot menu or the keyboard equivalents COMMAND-F for Faster and COMMAND-S for Slower.

Depth cuing and showing of the axes are controlled by items on the plot menu.

If you click the mouse in one of the Pitch, Roll or Yaw squares while holding down the shift key the plot will start to rotate and continue to rotate after the mouse button has been released.