More on Categorical Data

University of Iowa

College of Liberal Arts and Sciences

Data Formats
Two Data Sets
- Hair and Eye Color
- Arthritis Data
Bar Charts
- Hair and Eye Color
- Arthritis Data
Spine Plot
Doubledecker Plots
Mosaic Plots
Spinograms and CD Plots
Uncertainty Representation
References
Some Other Visualizations
- Stream Graphs
- Alluvial plots

Visualizing the distribution of multiple categorical variables involves visualizing counts and proportions.

Distributions can be viewed as

joint distributions;
conditional distributions.

The most common approaches use variants of bar and area charts.

The resulting plots are often called mosaic plots.

Data Formats

Purely categorical data can be

in raw form, one row per observation
aggregated into counts for unique level combinations
cross-tabulated

Data that includes categorical and numerical variables is usually in raw form.

count from dplyr produces aggregated data from raw data.
as.data.frame converts cross-tabulated data to aggregated form.

The notes on visualizing a categorical variable provide more details and examples.

Two Data Sets

Hair and Eye Color

The cross-tabulated data in HairEyeColor was used previously:

HairEyeColorDF <- as.data.frame(HairEyeColor)
head(HairEyeColorDF)
##    Hair   Eye  Sex Freq
## 1 Black Brown Male   32
## 2 Brown Brown Male   53
## 3   Red Brown Male   10
## 4 Blond Brown Male    3
## 5 Black  Blue Male   11
## 6 Brown  Blue Male   50

Marginal distributions of the variables:

grid.arrange(ggplot(HairEyeColorDF) + geom_col(aes(Sex, Freq)),
             ggplot(HairEyeColorDF) + geom_col(aes(Hair, Freq)),
             ggplot(HairEyeColorDF) + geom_col(aes(Eye, Freq)),
             nrow = 1)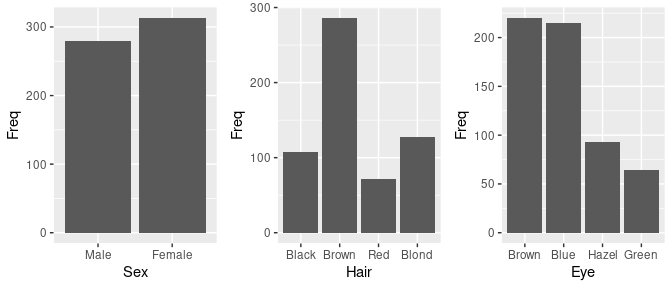

Arthritis Data

The vcd package includes the data frame Arthritis with several variables for 84 patients in a clinical trial for a treatment for rheumatoid arthritis.

The Improved variable is the response.
The predictors are Treatment, Sex, and Age.

library(vcd)
head(Arthritis)
##   ID Treatment  Sex Age Improved
## 1 57   Treated Male  27     Some
## 2 46   Treated Male  29     None
## 3 77   Treated Male  30     None
## 4 17   Treated Male  32   Marked
## 5 36   Treated Male  46   Marked
## 6 23   Treated Male  58   Marked

Counts for the categorical predictors:

xtabs(~ Treatment + Sex, data = Arthritis)
##          Sex
## Treatment Female Male
##   Placebo     32   11
##   Treated     27   14

Age distribution:

library(lattice)
histogram(~ Age | Sex * Treatment, data = Arthritis)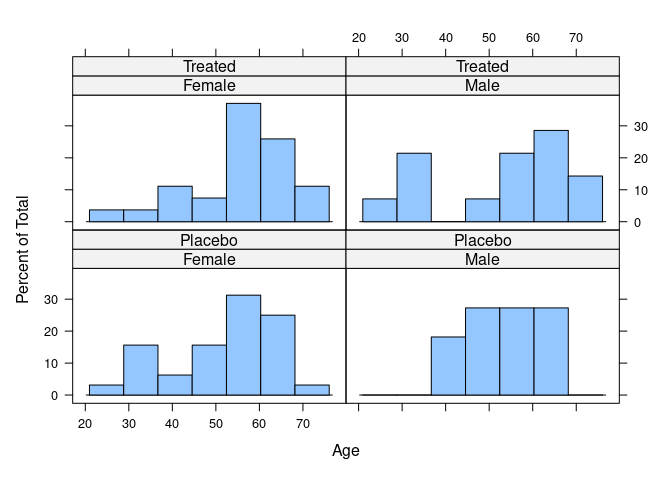

Bar Charts

Hair and Eye Color

Default bar charts show the individual count or joint proportions.

For the hair-eye color aggregated data counts:

ggplot(HairEyeColorDF) +
    geom_col(aes(Eye, Freq, fill = Sex)) +
    facet_wrap(~ Hair)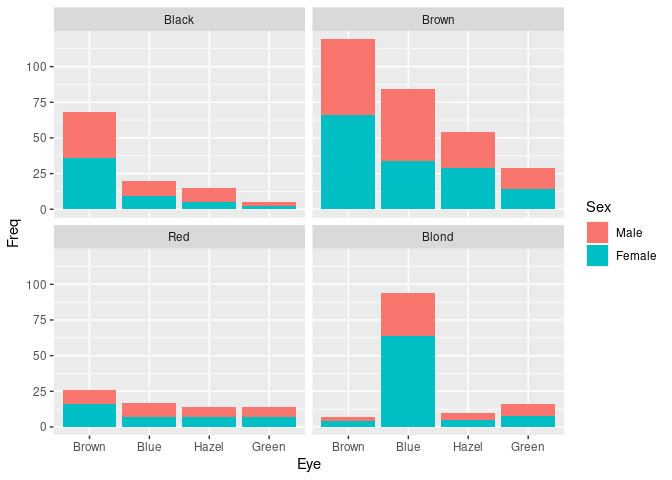

Joint proportions:

ggplot(mutate(HairEyeColorDF, Prop = Freq / sum(Freq))) +
    geom_col(aes(Eye, Prop, fill = Sex)) +
    facet_wrap(~ Hair)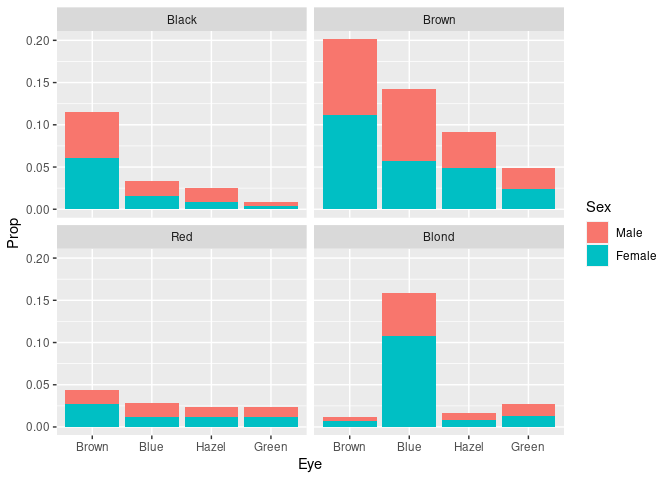

Differing frequencies of the hair colors are visible.
Conditional distributions of eye color within hair color are harder to compare.

Showing conditional distributions requires computing proportions within groups.

For the joint conditional distribution of sex and eye color given hair color:

peh <- mutate(group_by(HairEyeColorDF, Hair), Prop = Freq / sum(Freq))
ggplot(peh) +
    geom_col(aes(Eye, Prop, fill = Sex)) +
    facet_wrap(~ Hair)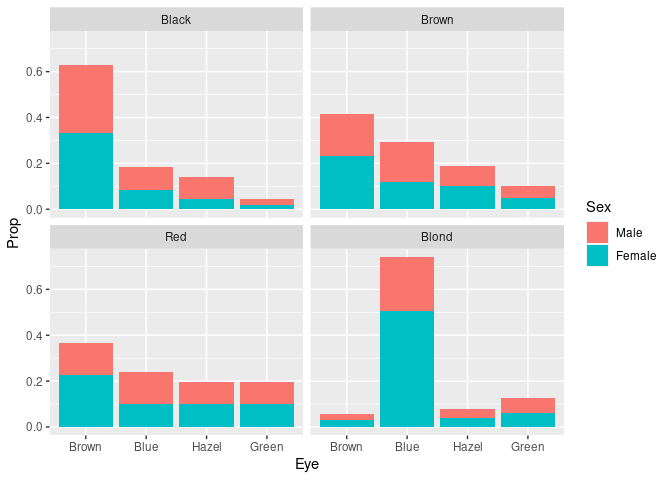

It is easier to compare the skewness of the eye color distributions for black, brown, and red hair.
Assessing the proportion of females or males withing the different groups is possible but challenging since it requires relative length comparisons.

To more clearly see the that the proportion of females among subjects with blond hair and blue eyes is higher than for other hair/eye color combinations we can look at the conditional distribution of sex given hair and eye color

pseh <- mutate(group_by(HairEyeColorDF, Hair, Eye), Prop = Freq / sum(Freq))
ggplot(pseh) +
    geom_col(aes(Eye, Prop, fill = Sex)) +
    facet_wrap(~ Hair, nrow = 1) +
    theme(axis.text.x = element_text(angle = 45, hjust = 1))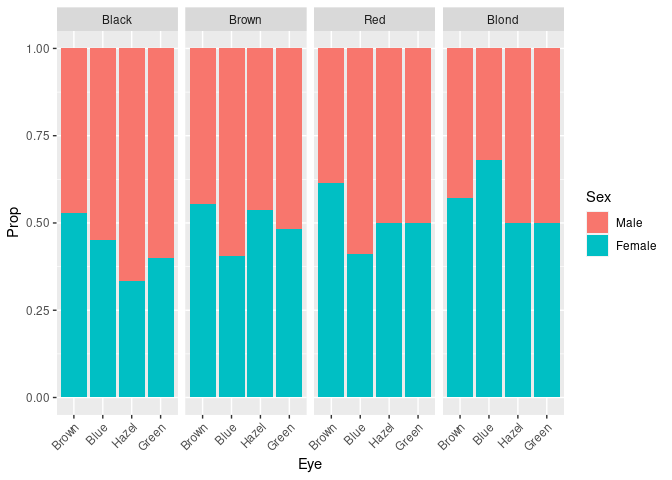

This plot can also be obtained as

ggplot(HairEyeColorDF) +
    geom_col(aes(Eye, Freq, fill = Sex), position = "fill") +
    facet_wrap(~ Hair, nrow = 1) +
    theme(axis.text.x = element_text(angle = 45, hjust = 1))

This visualization no longer shows the that some of the hair/eye color combinations are more common than others.

Arthritis Data

For the raw arthritis data, geom_bar computes the aggregate counts and produces a stacked bar chart by default:

p <- ggplot(Arthritis, aes(Sex, fill = Improved)) + facet_wrap(~ Treatment)
p + geom_bar()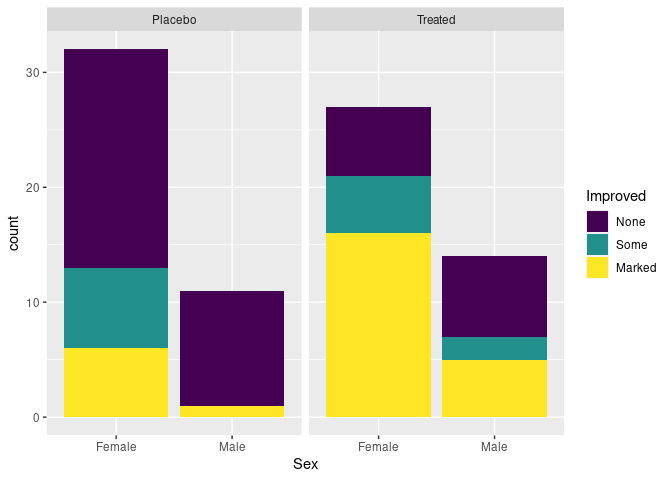

Specifying position = "dodge" produces a side-by-side plot:

p + geom_bar(position = "dodge")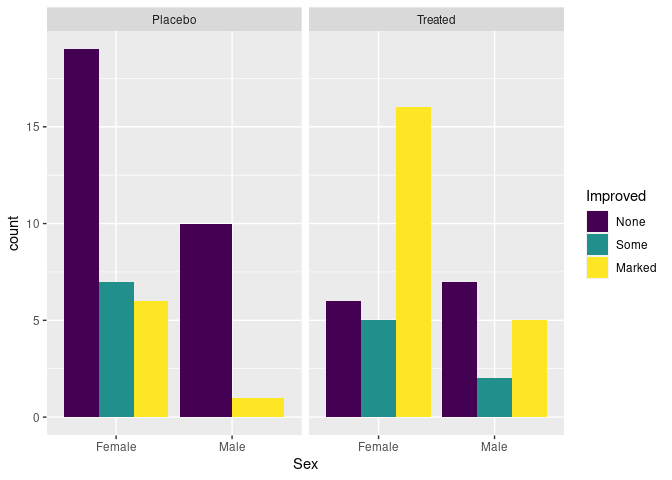

There are no cases of male patients on placebo reporting Some improvement, resulting in wider bars for the other options.

One way to produce a zero height bar:

aggregate with count, and
use complete from tidyr

library(tidyr)
atsi <- count(Arthritis, Treatment, Sex, Improved)
atsi <- complete(atsi, Treatment, Sex, Improved, fill = list(n = 0))
ggplot(atsi, aes(Sex, n, fill = Improved)) +
    geom_col(position = "dodge") +
    facet_wrap(~ Treatment)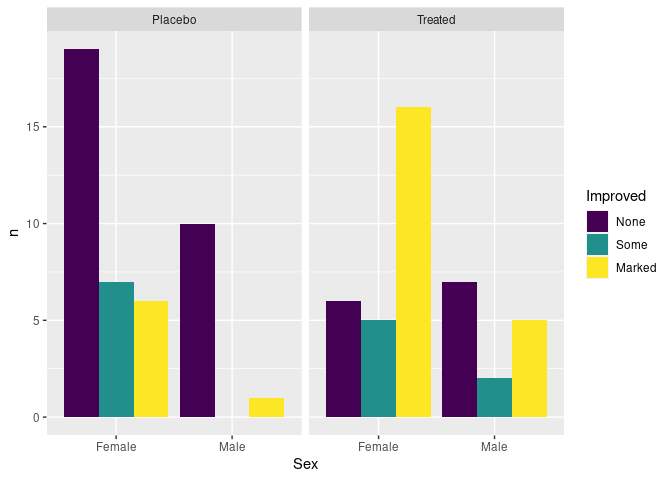

Showing conditional distributions instead of joint proportions:

patsi <- mutate(group_by(atsi, Treatment, Sex), prop = n / sum(n))
ggplot(patsi) +
    geom_col(aes(x = Sex, y = prop, fill = Improved),
             position = "dodge") +
    facet_wrap(~ Treatment)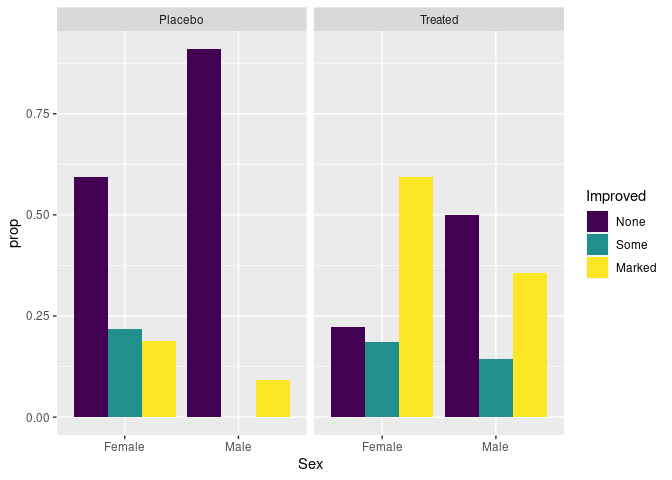

Stacked bar charts with height one are another option for make conditional distributions easier to compare:

p + geom_bar(position = "fill")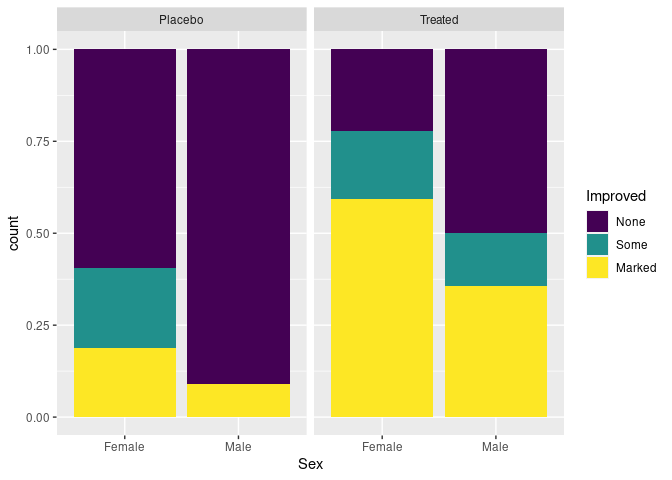

Ordering of variables affects which comparisons are easier.

A researcher might want to emphasize the differential response among males and females.
A patient might prefer to be able to focus on whether the treatment is effective for them:

ggplot(Arthritis, aes(Treatment, fill = Improved)) +
    geom_bar(position = "fill") +
    facet_wrap(~ Sex)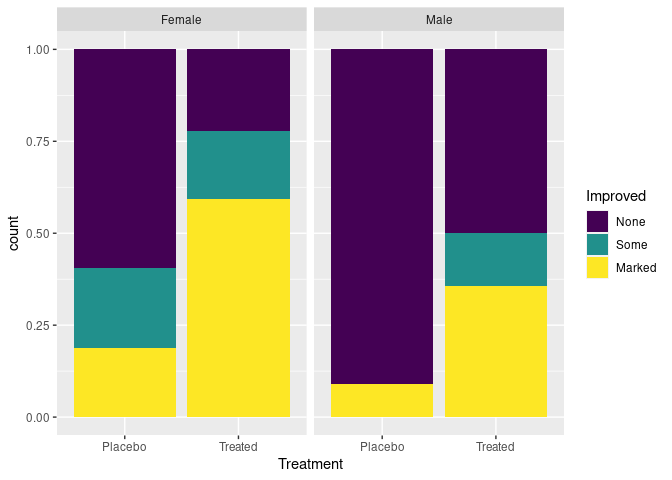

The stacked bar chart is effective for two categories, and a few more if they are ordered.
Providing a visual indication of uncertainty in the estimates is a challenge. The standard errors are around 0.1.
The proportions of each treatment group that are male or female could be encoded in the bar width.
The resulting plot is called a spine plot.
Neither ggplot2 nor lattice seem to make this easy.

Spine Plot

Spine plots are a special case of mosaic plots, and can be seen as a generalization of stacked bar plots.

The proportions for the categories of a predictor variable are encoded in the bar widths.
Spine plots are provided by the base graphics function spineplot and the vcd function spline.
vcd plots are built on the grid graphics system, like lattice and ggplot2 graphics.
The ggmosaic package provides support for mosaic plots in the ggplot framework.

Spine plots for the arthritis data using spineplot:

library(forcats)
Arth <- mutate(Arthritis, Improved = fct_rev(Improved))
ArthP <- filter(Arth, Treatment == "Placebo")
ArthT <- filter(Arth, Treatment == "Treated")
opar <- par(mfrow = c(1, 2))
spineplot(Improved ~ Sex, data = ArthP, main = "Placebo")
spineplot(Improved ~ Sex, data = ArthT, main = "Treatment")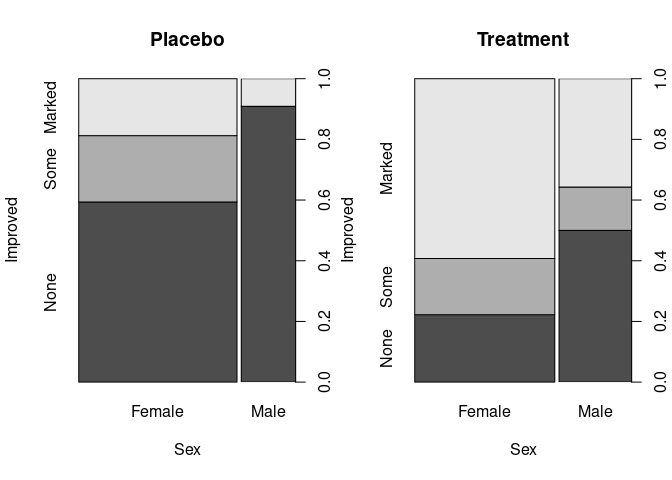

par(opar)

spineplot can use raw data or cross-tabulated data:

spineplot(xtabs(Freq ~ Hair + Sex, HairEyeColorDF)[, 2 : 1])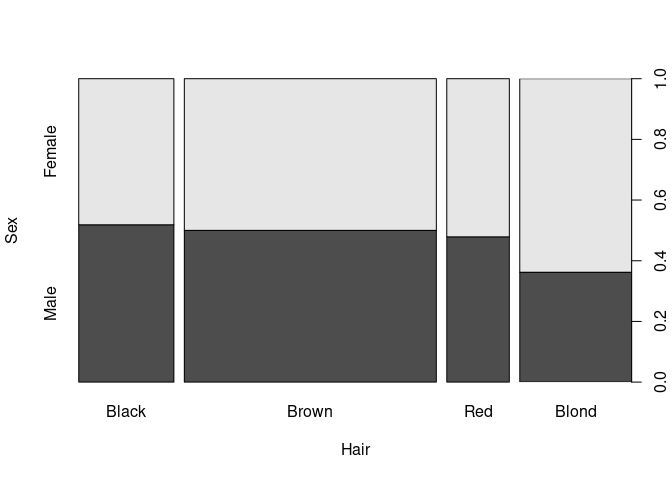

Using geom_mosaic from ggmosaic and the raw arthritis data:

library(ggmosaic)
ggplot(Arth) +
    geom_mosaic(aes(x = product(Sex), fill = Improved)) +
    facet_wrap(~ Treatment)
## Warning: `unite_()` was deprecated in tidyr 1.2.0.
## ℹ Please use `unite()` instead.
## ℹ The deprecated feature was likely used in the ggmosaic package.
##   Please report the issue at <https://github.com/haleyjeppson/ggmosaic>.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.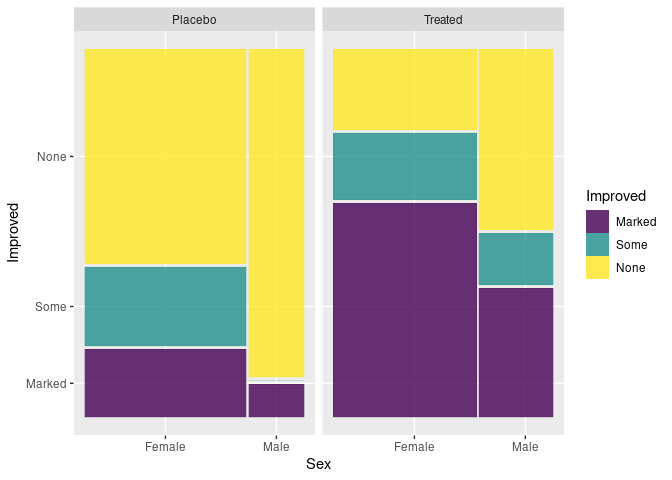

For aggregate counts use the weight aesthetic:

HDF <- mutate(HairEyeColorDF, Sex = fct_rev(Sex))
ggplot(HDF) +
    geom_mosaic(aes(weight = Freq, x = product(Hair), fill = Sex))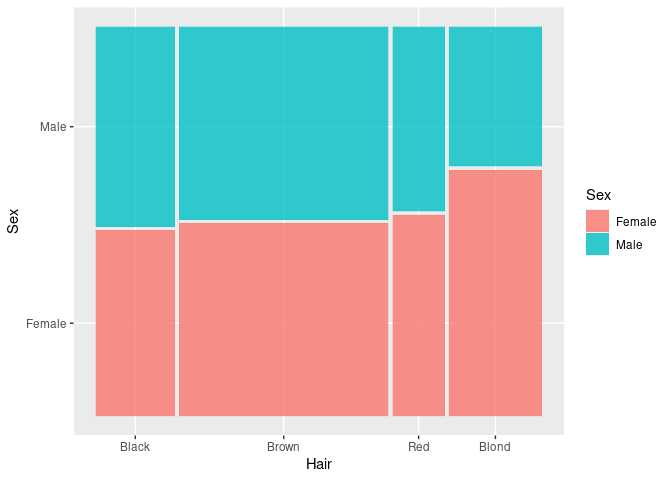

Doubledecker Plots

Doubledecker plots can be viewed as a generalization of spine plots to multiple predictors.

Package vcd provides the doubledecker function.

doubledecker(Improved ~ Treatment + Sex, data = Arthritis)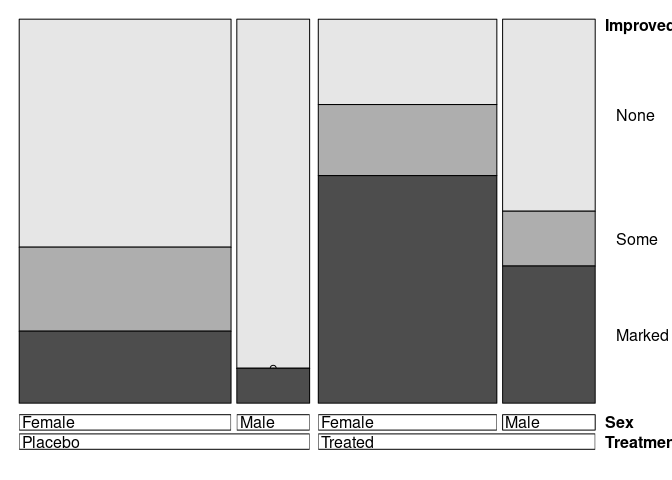

doubledecker(Improved ~ Sex + Treatment, data = Arthritis)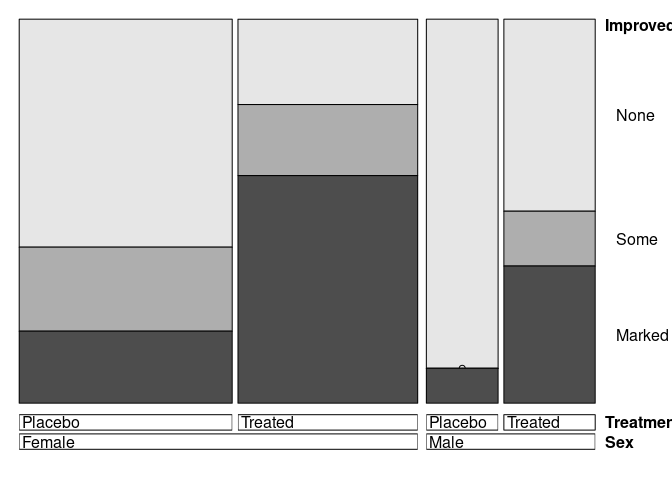

doubledecker also works with raw or cross-tabulated data:

doubledecker(xtabs(Freq ~ Hair + Eye + Sex, HairEyeColorDF))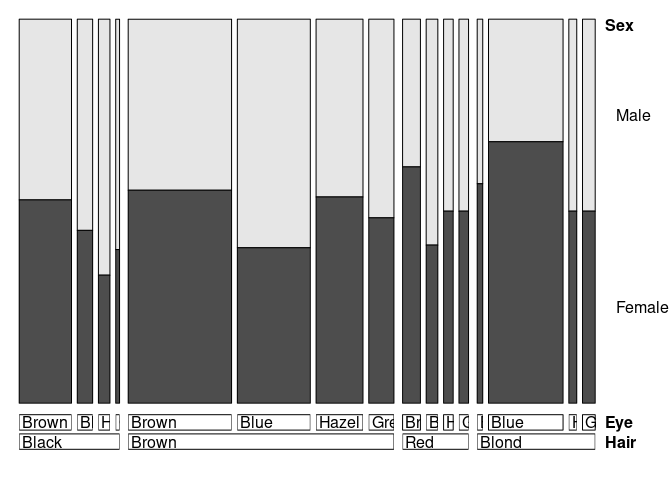

Using ggmosaic:

ggplot(Arth) +
    geom_mosaic(aes(x = product(Sex, Treatment), fill = Improved),
                divider = ddecker()) +
    theme(axis.text.x = element_text(angle = 15, hjust = 1))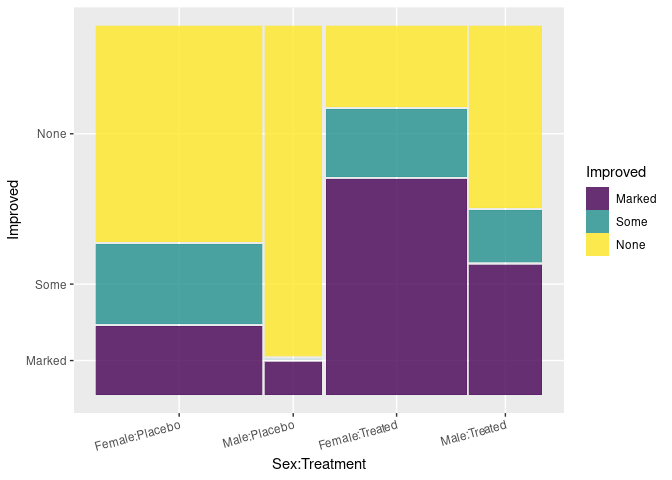


ggplot(Arth) +
    geom_mosaic(aes(x = product(Treatment, Sex), fill = Improved),
                divider = ddecker()) +
    theme(axis.text.x = element_text(angle = 15, hjust = 1))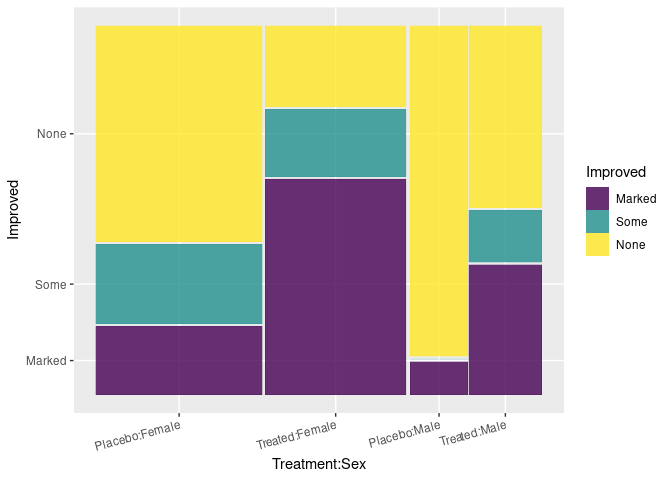


ggplot(HDF) +
    geom_mosaic(aes(weight = Freq, x = product(Eye, Hair), fill = Sex),
                divider = ddecker()) +
    theme(axis.text.x = element_text(angle = 35, hjust = 1))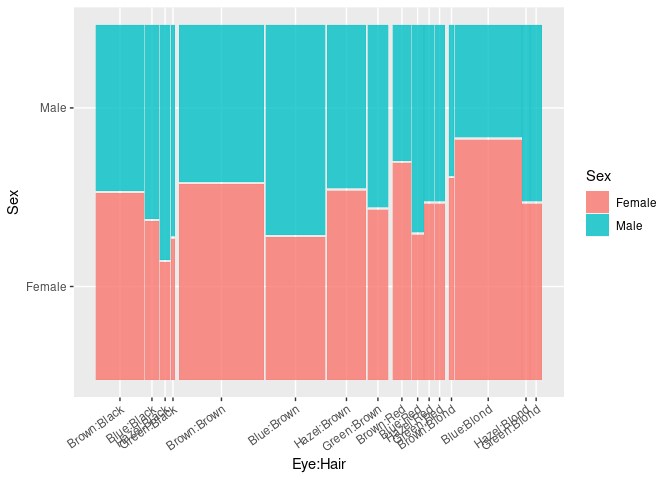

Mosaic Plots

Mosaic plots recursively partition the axes to represent counts of categorical variables as rectangles.

Base graphics provides mosaicplot;
vcd provides mosaic.

A Mosaic plot for the predictors Sex and Treatment:

mosaicplot(~ Sex + Treatment, data = Arthritis)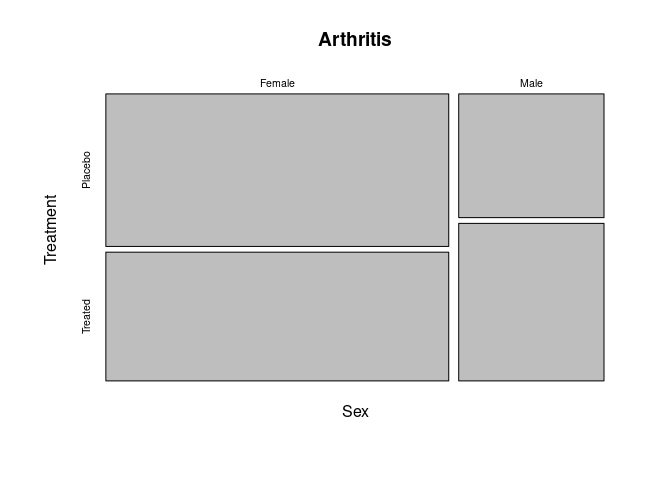

Adding Improved to the joint distribution:

vcd::mosaic(~ Sex + Treatment + Improved, data = Arthritis)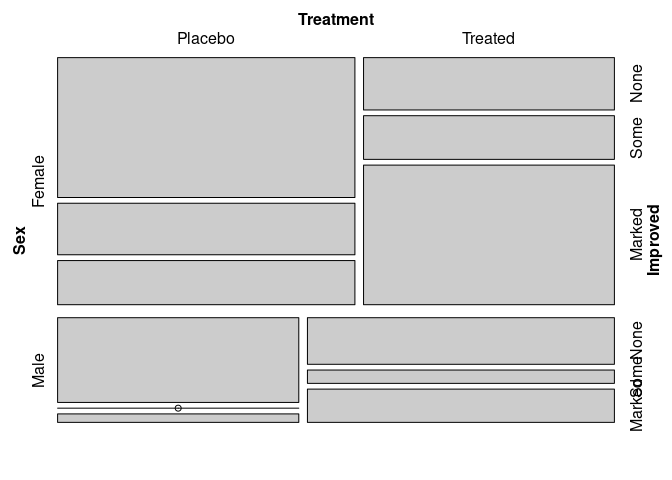

Identifying Improved as the response:

vcd::mosaic(Improved ~ Sex + Treatment, data = Arthritis)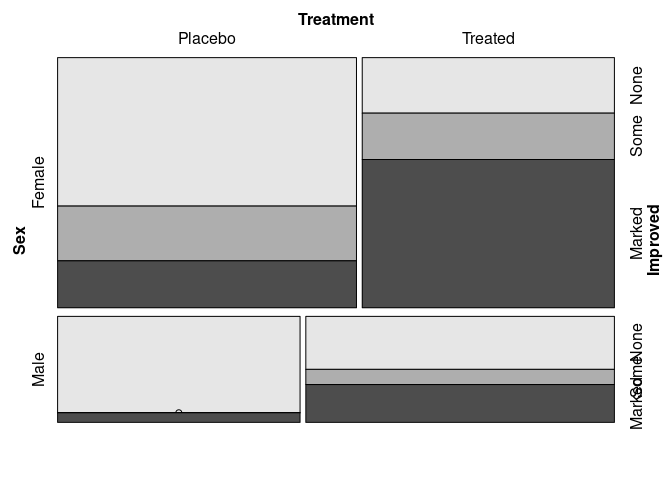

Matching the doubledecker plots:

vcd::mosaic(Improved ~ Treatment + Sex, data = Arthritis,
            split_vertical = c(TRUE, TRUE, FALSE))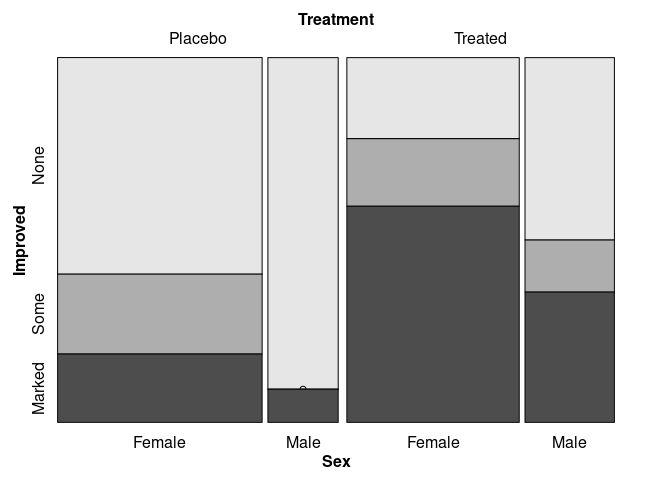

vcd::mosaic(Improved ~ Sex + Treatment, data = Arthritis,
            split_vertical = c(TRUE, TRUE, FALSE))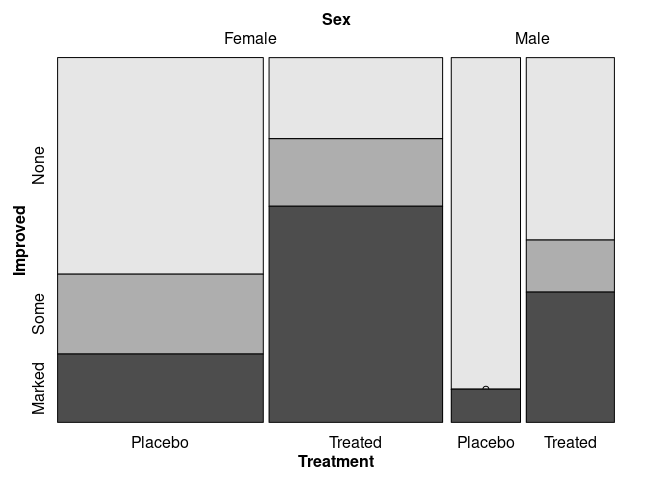

A mosaic plot for all bivariate marginals:

pairs(xtabs(~ Sex + Treatment + Improved, data = Arthritis))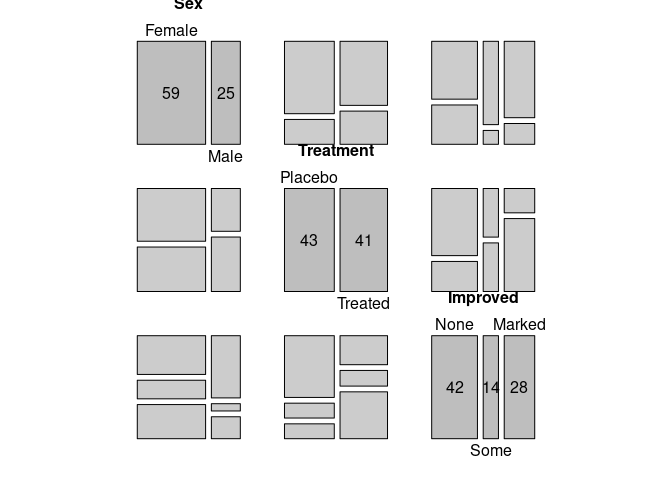

Spinograms and CD Plots

Spinograms and CD plots show the conditional distribution of a categorical variable given the value of a numeric variable.

Spinograms use the same binning as a histogram and then create a spine plot.
CD plots use a smoothing or density estimation approach.

A spinogram for Improved against Age:

spineplot(Improved ~ Age, data = ArthT)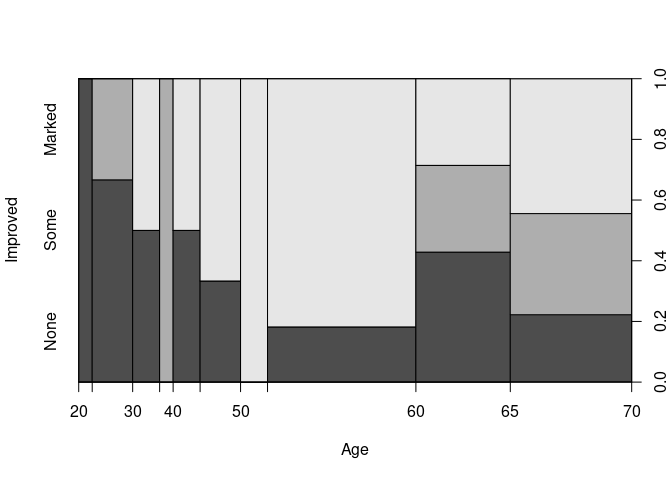

This is based on the histogram

hist(ArthT$Age, breaks = 13)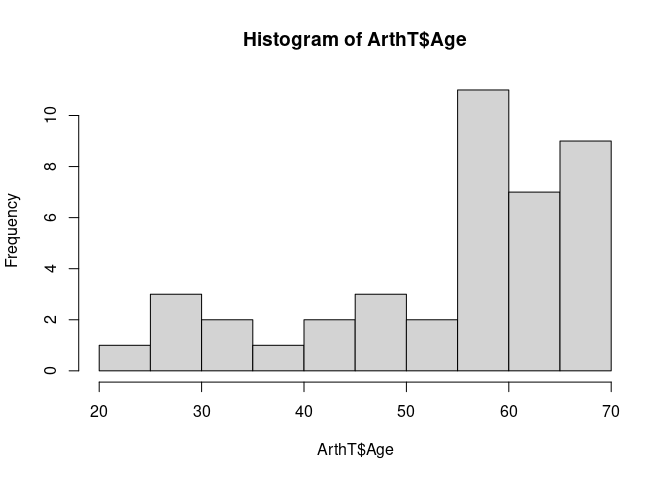

Spinograms for each level of Sex and Treated:

ArthTF <- filter(ArthT, Sex == "Female")
ArthTM <- filter(ArthT, Sex == "Male")
ArthPF <- filter(ArthP, Sex == "Female")
ArthPM <- filter(ArthP, Sex == "Male")

opar <- par(mfrow = c(2, 2))
spineplot(Improved ~ Age, data = ArthTM, main = "TM")
spineplot(Improved ~ Age, data = ArthTF, main = "TF")
spineplot(Improved ~ Age, data = ArthPM, main = "PM")
spineplot(Improved ~ Age, data = ArthPF, main = "PF")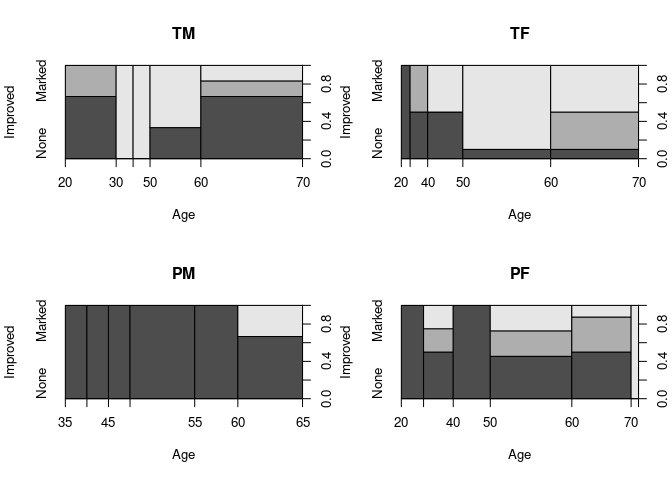

par(opar)

CD plots estimate the conditional density of the x variable given the levels of y, weighted by the marginal proportions of y and use these to estimate cumulative probabilities.

The slice at a particular x level visualizes the conditional distribution of y given x at that level.
The cd_plot function from the vcd package produces a CD plot using grid graphics.
The cdplot function from the base `graphics package provides the same plots using base graphics.

Analogous CD plots for the Arthritis data:

cd_plot(Improved ~ Age, data = ArthT)

cd_plot(Improved ~ Age, data = ArthTM, main = "TM")
cd_plot(Improved ~ Age, data = ArthTF, main = "TF")
cd_plot(Improved ~ Age, data = ArthPM, main = "PM")
cd_plot(Improved ~ Age, data = ArthPF, main = "PF")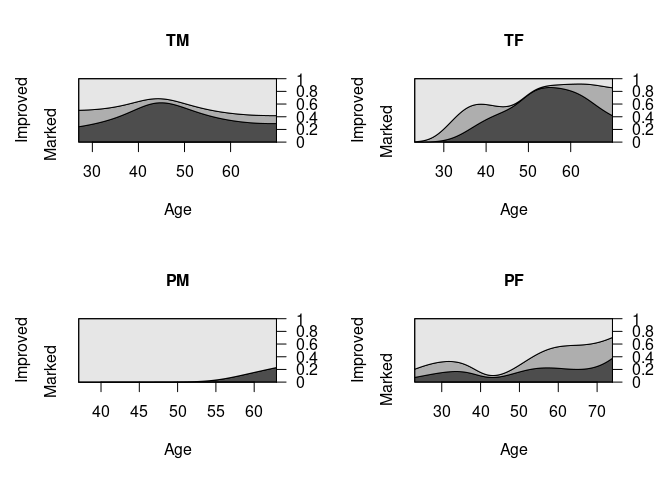

It may be helpful to consider an age grouping like

cut(Arthritis$Age, c(0, 40, 60, 100))

This loses some information but may simplify the analysis.
This can also allow the reduction of data to cell counts to help with very large data sets.

Uncertainty Representation

Categorical data are often analyzed by fitting models representing conditional independence structures.

Plotting residuals from these models can help assess how well they fit.
mosaic supports using color to represent magnitude of residuals for comparing to a simple independence model.

For the Arthritis data, assessing independence of Treatment and Improved produces:

vcd::mosaic(~ Treatment + Improved, data = Arthritis, gp = shading_max)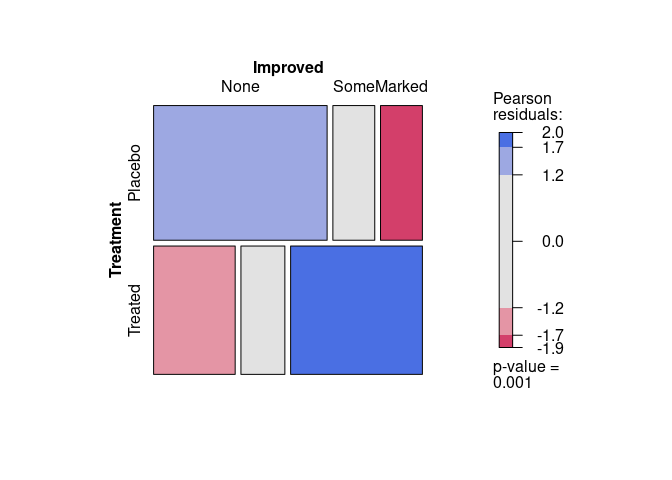

Another visualization of the residuals is the association plot produced by assoc:

assoc(~ Treatment + Improved, data = Arthritis, gp = shading_max)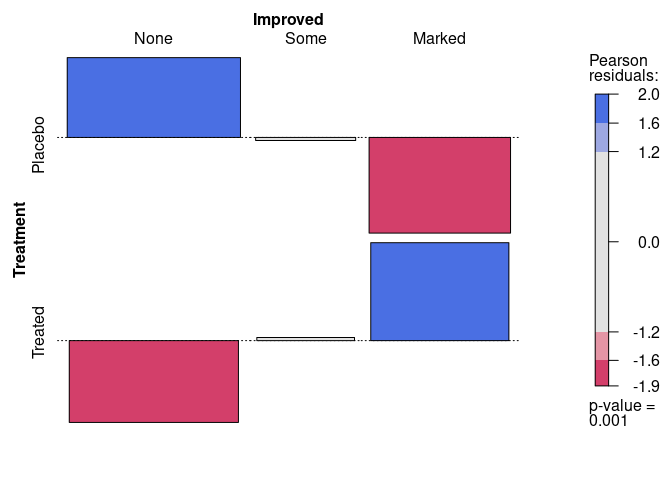

References

The vignette Residual-Based Shadings in vcd in the vcd package.
Zeileis, Achim, David Meyer, and Kurt Hornik. “Residual-based shadings for visualizing (conditional) independence.” Journal of Computational and Graphical Statistics 16, no. 3 (2007): 507-525.

Several other experimental mosaic plot implementations are available for ggplot.

Some Other Visualizations

Stream Graphs

Stream graphs are a generalization of stacked bar charts plotted against a numeric variable.
In some cases the origins of the bars are shifted to improve some aspect of the overall visualization.
An early example is the Baby Name Voyager.
A NY Times visualization of movie box office results is another example.
Some R implementation on GitHub:
- ggTimeSeries
- streamgraph, which uses D3.

After installing streamgraph with

devtools::install_github("hrbrmstr/streamgraph")

a stream graph for movie genres (these are not mutually exclusive):

library(streamgraph)
library(tidyverse)
genres <- c("Action", "Animation", "Comedy", "Drama", "Documentary", "Romance")
mymovies <- select(ggplot2movies::movies, year, one_of(genres))
mymovies_long <- gather(mymovies, genre, value, -year)
movie_counts <- count(mymovies_long, year, genre)
streamgraph(movie_counts, "genre", "n", "year")
## Warning in widget_html(name, package, id = x$id, style = css(width =
## validateCssUnit(sizeInfo$width), : streamgraph_html returned an object of class
## `list` instead of a `shiny.tag`.
## Warning: `bindFillRole()` only works on htmltools::tag() objects (e.g., div(),
## p(), etc.), not objects of type 'list'.

Alluvial plots

These are also known as

parallel sets, or
Sankey diagrams.

They can be viewed as a parallel coordinates plot for categorical data.

Using the alluvial package:

library(alluvial)
pal <- RColorBrewer::brewer.pal(2, "Set1")
## Warning in RColorBrewer::brewer.pal(2, "Set1"): minimal value for n is 3, returning requested palette with 3 different levels
with(HDF,
     alluvial(Hair, Eye, Sex, freq = Freq, col = pal[as.numeric(Sex)]))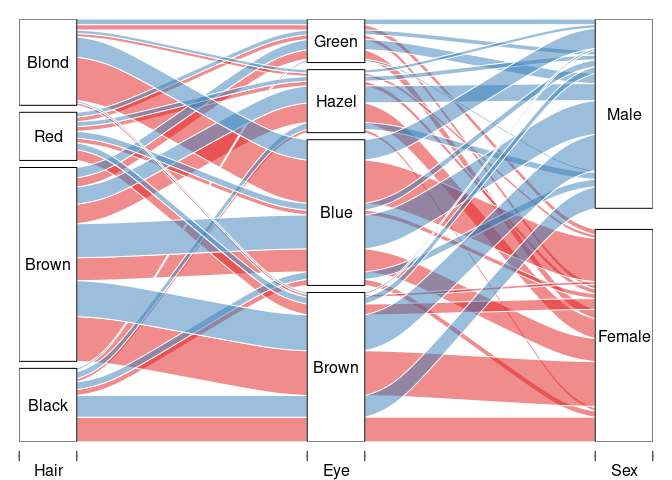


with(count(Arth, Improved, Treatment, Sex),
     alluvial(Improved, Treatment, Sex, freq = n, col = pal[as.numeric(Sex)]))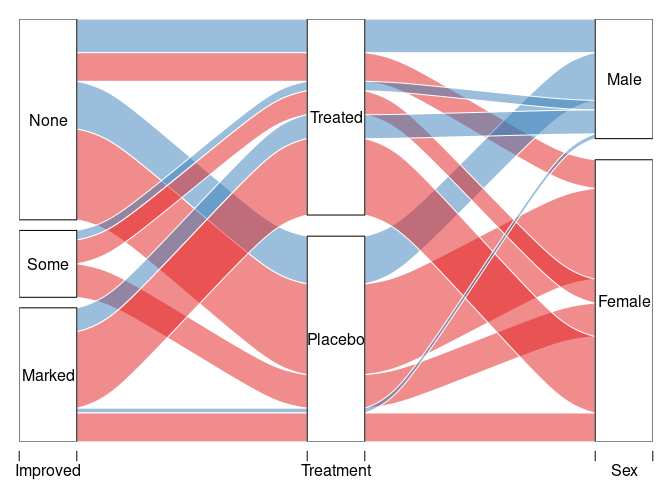

Using package ggforce:

library(ggforce)
sHDF <- gather_set_data(HDF, 1 : 3)
sHDF <- mutate(sHDF, x = fct_inorder(factor(x)))
ggplot(sHDF, aes(x, id = id, split = y, value = Freq)) +
    geom_parallel_sets(aes(fill = Sex), alpha = 0.5, axis.width = 0.1) +
    geom_parallel_sets_axes(axis.width = 0.1) +
    geom_parallel_sets_labels(colour = "white") +
    scale_fill_manual(values = c(Male = pal[2], Female = pal[1]))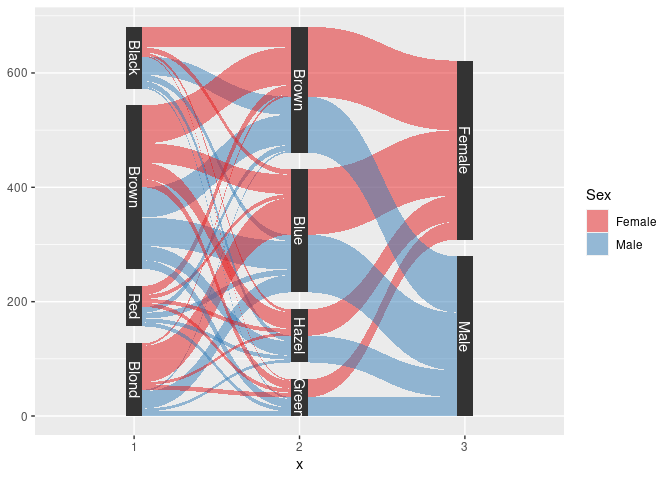


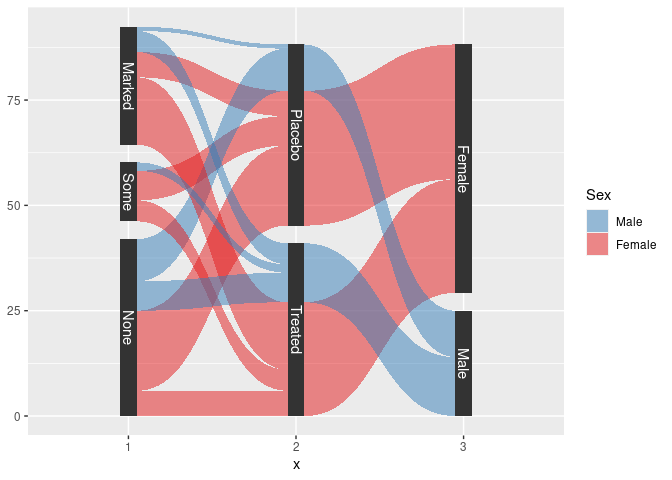
sArth <- mutate(Arth,
                Improved = factor(Improved, ordered = FALSE)) %>%
    count(Improved, Treatment, Sex) %>%
    gather_set_data(1 : 3)
sArth <- mutate(sArth, x = fct_inorder(factor(x)), Sex = fct_rev(Sex))
ggplot(sArth, aes(x, id = id, split = y, value = n)) +
    geom_parallel_sets(aes(fill = Sex), alpha = 0.5, axis.width = 0.1) +
    geom_parallel_sets_axes(axis.width = 0.1) +
    geom_parallel_sets_labels(colour = "white") +
    scale_fill_manual(values = c(Male = pal[2], Female = pal[1]))