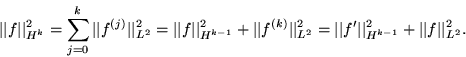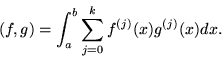| Name | Description | Norm |
| C[a,b] | Continuous functions on [a,b] | |
| L1(a,b) | Integrable functions: |
|
| L2(a,b) | Square integrable functions: |
|
| Lp(a,b) | p-integrable functions ( |
|
| H1(a,b) | Sobolev space: |
||f||H12=||f(x)||L22+||f'(x)||L22 |
| Name | Description | Norm |
| C[a,b] | Continuous functions on [a,b] | |
| L1(a,b) | Integrable functions: |
|
| L2(a,b) | Square integrable functions: |
|
| Lp(a,b) | p-integrable functions ( |
|
| H1(a,b) | Sobolev space: |
||f||H12=||f(x)||L22+||f'(x)||L22 |
In the abstract, we will be dealing with a set of functions X with a
norm ![]() .So far, we don't know what to do with limits of objects xk in X.
.So far, we don't know what to do with limits of objects xk in X.
If we were talking about real numbers, we would expect that a sequence
like 1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ...would converge.
If our universe only consisted of rational numbers, then we would be
in trouble because they could be converging to
![]() , which is not rational.
But with real numbers, any sequence like 1, 1.4, 1.41, 1.414,
1.4142, 1.41421, ..., which adds one new digit with each element in
the sequence, converges.
, which is not rational.
But with real numbers, any sequence like 1, 1.4, 1.41, 1.414,
1.4142, 1.41421, ..., which adds one new digit with each element in
the sequence, converges.
What sequences xk in a set X with norm ![]() ``ought'' to
converge?
The answer that we use is the idea of a Cauchy sequence:
``ought'' to
converge?
The answer that we use is the idea of a Cauchy sequence:
A sequence xk is a Cauchy sequence if for every ![]() there is
an N such that
there is
an N such that ![]() implies
implies ![]() .
.
A space (consisting of X with norm ![]() ) is complete
if every Cauchy sequence has a limit.
) is complete
if every Cauchy sequence has a limit.
The first example of a complete space is the real line.
The first example of a complete function space that most people meet
is the space of continuous functions on [a,b], denoted C[a,b],
with norm ![]() .
.
All of the examples from §2 are complete function spaces.
Complete normed spaces are called Banach spaces after the Polish mathematician, Stefan Banach.
One of the most important function spaces is L2(a,b) - the space
of square integrable functions on the interval (a,b).
The L2 norm is ![]() .
.
The precise definition of L2(a,b) is based on Lebesgue integration theory, which is beyond the scope of these notes. The trickiest aspect of L2(a,b) is that we cannot distinguish between functions in L2(a,b) that differ only at a single point, or at a countable number of points.
[Technically, we regard f=g if the set ![]() is a null set; that is, if changing the values of this set has
no effect on any integrals.]
is a null set; that is, if changing the values of this set has
no effect on any integrals.]
One of the more important aspects of L2(a,b) is that the norm comes from an inner product:
![]()
![]()
Now we will see the Cauchy inequality holds for these inner-product spaces:
![]()
Proof.
For any a, ![]() , so the quadratic in a,
, so the quadratic in a,
![]()
This makes L2(a,b) an example of a complete inner product space, or as it is better known, L2(a,b) is a Hilbert space.
Since functions in L2(a,b) are integrable, they represent distributions; L2 is a subset of the space of distributions.
Sobolev spaces are Banach spaces where the norm involves derivatives, or at least, something other than just function values. The simplest of these is H1(a,b).
H1(a,b) is the Banach space of functions
![]()
||f||H12 = ||f||L22 + ||f'||L22.
Actually, we need to be a little careful about ``![]() '',
since we need to keep a tight connection between f and f'.
For example, if we think of the Heaviside function H(x) of
§1.1,
H'(x)=0 for all x, except for x=0, where it is undefined.
Thus as far as integrals are concerned, we cannot distinguish between
H'(x) and the zero function.
On the other hand, H(x) is definitely not constant.
So we would like to keep this function out of the Sobolev space H1(a,b).
'',
since we need to keep a tight connection between f and f'.
For example, if we think of the Heaviside function H(x) of
§1.1,
H'(x)=0 for all x, except for x=0, where it is undefined.
Thus as far as integrals are concerned, we cannot distinguish between
H'(x) and the zero function.
On the other hand, H(x) is definitely not constant.
So we would like to keep this function out of the Sobolev space H1(a,b).
There are two ways of avoiding functions like H(x):
The Sobolev space H1(a,b) has an inner product that defines the norm:
![]()
Higher order Sobolev spaces can be defined:
![]()