5.2
5.3
Section Summary
The gapsfor
,
, and
are calculated in this section by comparing the length of a segment of the unit circle with the vertical and horizontal projections from the ends of the segment.
The derivative of sine in radians is cosine and the derivative of cosine in radians is -sine.
These important facts can be seen by magnifying the unit circle.
We assume that you know the definition of radian measure of angles and the associated fact that
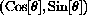 is the (x,y)-point on the unit circle at the angle
is the (x,y)-point on the unit circle at the angle
 , measured counterclockwise from the x-axis. (See Chapter 28, Section 5 and Figure CD-5.1.)
, measured counterclockwise from the x-axis. (See Chapter 28, Section 5 and Figure CD-5.1.)
In this section, we use the informal version of Definition 5.5 and work from the relationship between the sine and cosine and the length along the unit circle shown on Figure CD-5.1. Consider what happens as we move from a point
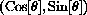 to a nearby point
to a nearby point
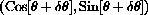 . We magnify the unit circle, noting on Figure CD-5.2 that the more we magnify, the straighter the magnified portion of the circle appears.
. We magnify the unit circle, noting on Figure CD-5.2 that the more we magnify, the straighter the magnified portion of the circle appears.
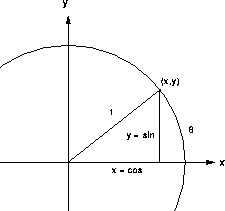
Figure CD-5.1: Sine and Cosine as a Point on the Unit Circle
The figure with small
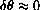 appears to be a triangle at magnification
appears to be a triangle at magnification
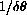 . The length of the hypotenuse of the apparent triangle is
. The length of the hypotenuse of the apparent triangle is
 because we use radian measure. (Degrees are not the distance along a unit circle.) The radii coming from the larger figure appear to meet it at right angles, so the apparent triangle is similar to the large triangle at the left with hypotenuse 1 and sides
because we use radian measure. (Degrees are not the distance along a unit circle.) The radii coming from the larger figure appear to meet it at right angles, so the apparent triangle is similar to the large triangle at the left with hypotenuse 1 and sides
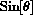 ,
,  . (You may have to do some geometry to convince yourself of this, since the corresponding edges are at right angles to one another.) The sides of the apparent triangle are the differences in sine and cosine, with cosine decreasing - hence a negative sign.
. (You may have to do some geometry to convince yourself of this, since the corresponding edges are at right angles to one another.) The sides of the apparent triangle are the differences in sine and cosine, with cosine decreasing - hence a negative sign.
Figure CD-5.2 is the microscopic view of the circle that gives us the results
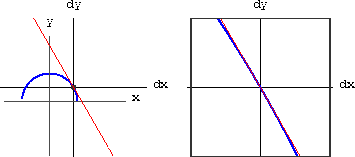
Figure CD-5.2: Derivatives of sine and cosine
Consider the apparent similarity, comparing the long sides of the two triangles,
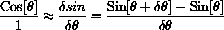
Because we only know the apparent triangle up to a small error, we write only approximate similarity. To be explicit, let the difference equal,

Now do a little algebra to see,
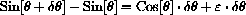
with
 whenever
whenever
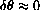 . This has the form
. This has the form
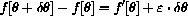
with
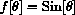 ,
, 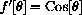 , and proves half of the following:
, and proves half of the following:
For
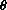 in radians,
in radians,
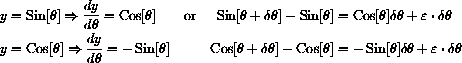
with
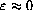 if
if
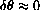 (
(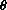 can take any value.)
can take any value.)
Example CD-5.1 Increments of Sine
The most important meaning of the increment formula for
 is simply that a small piece of the graph is given by the linear equation with slope
is simply that a small piece of the graph is given by the linear equation with slope
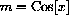 . For example, suppose that we want to estimate the sine of 29 degrees.
We know sine of 30 degrees and we can take the increment of -1 degree, using the "microscope equation." We must first convert to radian measure because the increment formulas above are valid only in radian measure.
We take
. For example, suppose that we want to estimate the sine of 29 degrees.
We know sine of 30 degrees and we can take the increment of -1 degree, using the "microscope equation." We must first convert to radian measure because the increment formulas above are valid only in radian measure.
We take
 and
and
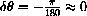 ,
,
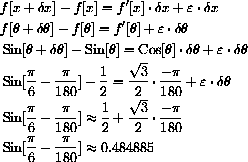
The computer's approximation of sine of 29 degrees is 0.48481.
Example CD-5.2 Limits of Sine
The previous example can be cast in limit notation as: Find
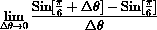
The solution is to recognize this as a special case of the limit defining the derivative,
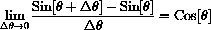
with
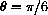 , or to use the increment approximation,
, or to use the increment approximation,

and recall that
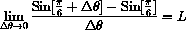
is the number L the expression approximates when
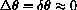 is small,
is small,
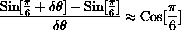
Rather than using the increment approximation based on a greatly magnified circle, we could use the exact addition formulas to obtain increments of trig functions.
In the case of the sine,
These are exact formulas for the increments, but we need to obtain the differential approximations
to complete the last step in proving the local linear approximation.
The point we wish to illustrate is this:
The differential
that discards the error term
We know
The point of the next problem is that we can compute the increments of the tangent function directly.
Later you will be able to differentiate
Problem CD-5.1
Derivative of Tangent (Optional)
5.4
The important functional identities of exponential functions are as follows:
For a positive base a>0 and any real numbers p and q
We want to use these properties to show what we need to estimate in order to differentiate log and exponential functions. (Practice with the rules can be found in Chapter 28, Section 4, if your skills are rusty.)
Example CD-5.3
The Exact Increment of y=ax
We write an exact formula for the difference
Notice that the last formula says
where the constant of proportionality
Example CD-5.4
Constant Rate of Change for Linear Functions
Suppose an unknown function f[x] increases by a constant amount k every time x increases by another constant amount h. What sort of function is f[x]? The statement that a constant change of h in input makes a constant change of k in output is
Linear functions change at a constant rate.
Exponential functions change by a constant percentage for a constant change in input.
Example CD-5.5
Constant PERCENTAGE Change for Exponential Functions
Suppose an unknown function f[x] increases by a constant percentage every time x increases by a constant h. For example, suppose f[x] increases by a third, 33.3%, every time x increases by 1/2. The change in f is
We try to find an exponential solution, f[x]=ax, of this functional equation
Example CD-5.6
Percentage Rate of Change as
When
Notice that, if the limit converges, the result says the following:
Moreover, the convergence is uniform for bounded x:
The "natural" base
A mathematically simpler approach is to take the definition:
This "definition" is based on two good guesses.
First, that the derivative of an exponential is proportional to the quantity.
We saw substantial evidence for this above.
Second, that some special number e makes the constant of proportionality equal to 1. The Project on Direct Computation of the Derivative of Exponentials shows you more details on this guess and gives you a way to compute
Technically, the approach relies on convergence of Euler's approximation to differential equations.
This is easier than the convergence problems in the direct approach to the exponential above and has many other applications. (We have not proved that Euler's approximation converges, but we have seen it work in several examples: S-I-R, the canary, and so forth.
The proof is in the Mathematical Background CD.) Once we have made this the "official" definition, we can use Euler's approximation to obtain the specific approximation
Once we know the derivative of the natural exponential and rules of differentiation, we can find the differentials of all exponentials.
For this reason, the natural log and exponential play a major role in science and mathematics.
Just as radian measure makes the calculus of trig functions "natural," the
How many 6-hour periods are there in t hours? (A formula.)
Give the number of cells n as a function of t,
Suppose at time t1 there are a billion cells.
How many are there at time t1+6?
What is the formula for the rate of growth of algae cells in a 6-hour period beginning at an unknown time t? (Compare your work to Problem CD-28.2 and the program ExpGth of Chapter 28.)
The next exercise has you practice using the functional identities for the logarithm.
The point of the exercise is that we need only one limit,
The next exercise has some practice using these derivatives in the increment approximation.
Do not use your calculator until you have written the symbolic expressions. (You do not have to use it at all, but you can check your work if you wish.)
5.5
We saw in the Exercise CD-3.2.1 that a function can be continuous but still not smooth or differentiable.
An official definition of continuity is the following
Intuitively, this just means that f[x] is close to f[a] when x is close to a, for every
INTUITIVE PROOF FOR f[x]:
Proof of continuity of f is easy algebraically but is obvious geometrically: A graph that is indistinguishable from linear clearly only moves a small amount in a small x-step.
Algebraically, we want to show that if
INTUITIVE PROOF FOR f'[x]:
Proof of continuity of f'[x] requires us to view the increment from both ends.
First take x=x1 and
NOTE:
The derivative defined in many calculus books is a weaker pointwise notion than the notion of smoothness we have defined.
The weak derivative function need not be continuous. (The same approximation does not apply at both ends with the weak definition.) This is explained in the Mathematical Background Chapter on "Epsilon - Delta" Approximations.
5.6
5.3.1
It is intuitively clear that magnified circles appear straighter and straighter, but complete justification of the local linearity of sine and cosine requires that we really show that the magnified increment of the circle is close to a triangle.
We will not do this here except to make two specific uses of identities that are important in their own right.
More details are contained in the Mathematical Background chapter on Functional Identities.
The formula
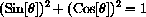
simply says that sine and cosine lie on the unit circle.
If
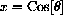 and
and
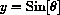 , x2+y2=1 is the equation of the unit circle.
, x2+y2=1 is the equation of the unit circle.
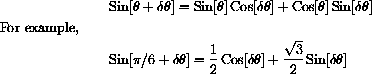
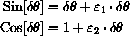
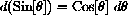
is a sort of simplified version of the functional identity

 .
.
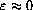 because magnified circles appear straighter and straighter as the magnification increases.
This observation gives us two interesting limits.
Since
because magnified circles appear straighter and straighter as the magnification increases.
This observation gives us two interesting limits.
Since

and since this is small for all
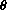 , we have
, we have
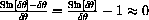 and
and
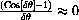 , or
, or
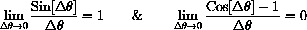
These limits are just the derivatives of sine and cosine at zero.
 above the point where
above the point where
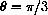 . Verify your prediction using the program Micro1D.
. Verify your prediction using the program Micro1D.
Use a powerful microscope to prove that the differential of cosine is minus sine,

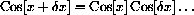 using the addition formula for cosine.
Compare the exact formula with the increment approximation obtained from the microscopic view of the circle.
What is the exact formula for
using the addition formula for cosine.
Compare the exact formula with the increment approximation obtained from the microscopic view of the circle.
What is the exact formula for
 ?
?
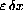 term.
Give your answer in terms of exact constants such as
term.
Give your answer in terms of exact constants such as
 and
and
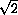 as well as numerically.
Compare your approximation with the computer or your scientific calculator's approximation.
as well as numerically.
Compare your approximation with the computer or your scientific calculator's approximation.
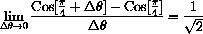
 on the Computer Run the program DfctLimit to show graphically that the gap errors of
on the Computer Run the program DfctLimit to show graphically that the gap errors of
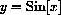 ,
, 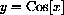 , and
, and
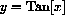 tend to zero AS FUNCTIONS OF x for appropriate compact intervals
tend to zero AS FUNCTIONS OF x for appropriate compact intervals
 . (HINT: Where are the functions and their derivatives defined?)
. (HINT: Where are the functions and their derivatives defined?)
 with rules from Chapter 6.
with rules from Chapter 6.
Find the differential of the tangent function by examining an increment in the figures below.
The segment on the line x=1 between two rays from the circle is the increment of the tangent, because SOH-CAH-TOA with adjacent side of length 1 gives
 as the length of the segment on x=1 between the x-axis and the ray.
as the length of the segment on x=1 between the x-axis and the ray.
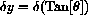 as its tiny vertical side is
as its tiny vertical side is
 , because the "height" is 1 for the "base" of
, because the "height" is 1 for the "base" of
 .
.
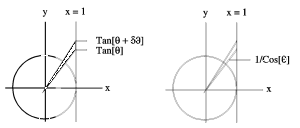
Figure CD-5.3: An increment of tangent and the secant Function
 out to x=1 is
out to x=1 is
 . Why?
. Why?

by finding the area of the circular sector at the left in Figure CD-5.4. (Note that the area of a circular sector of radius r and angle
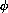 is
is
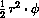 .)
.)
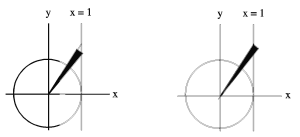
Figure CD-5.4: A lower estimate and an upper estimate

(What is the radius of the sector on the right in Figure CD-5.4?)
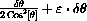 , with
, with
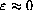 when
when
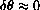 . Why? When is
. Why? When is
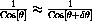 for
for
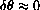 ?
?
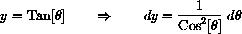
provided
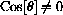 .
. Section Summary
The gaps
 for y=ex and
for y=ex and
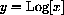 are discussed in this section.
are discussed in this section.
Theorem CD-5.1

 in terms of ax,
in terms of ax, 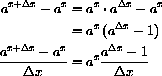
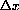 beginning at x is proportional to ax,
beginning at x is proportional to ax,
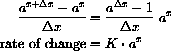
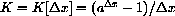 depends only on the change
depends only on the change
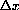 , not x.
, not x.
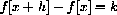
or the rate of change is constant
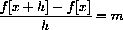
with m=k/h. It is easy to see that the linear function

with m=k/h has the needed property (it will satisfy the rate equation for every h.)

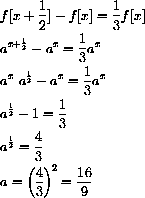
The function
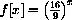 increases by one third every time x increases by one half.
increases by one third every time x increases by one half.
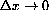
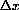 gets smaller and smaller, we would like to show that
gets smaller and smaller, we would like to show that
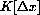 converges to a constant
converges to a constant
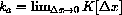 . In other words, when
. In other words, when
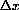 is small,
is small,
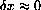 , we would like to find an expression for the difference quotient of exponentials of the form,
, we would like to find an expression for the difference quotient of exponentials of the form,
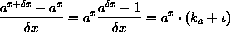
where the real constant ka depends only on a and
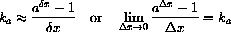
It turns out that the mysterious constant ka is
 (the natural logarithm) and
(the natural logarithm) and
 , but this approximation is difficult to establish directly.
, but this approximation is difficult to establish directly.
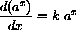
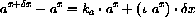
The gap
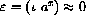 for all bounded x.
for all bounded x.
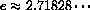 plays an important role in solving the problem because the number
plays an important role in solving the problem because the number
 is the unique number that makes
is the unique number that makes
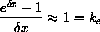
for
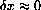 , that is, ka=1 when a=e.
, that is, ka=1 when a=e.
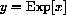 is officially defined to be the unique solution to
is officially defined to be the unique solution to
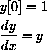
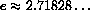 .
.
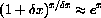
We postpone further discussion to Chapter 8 but give the derivatives now.
You may use these results as needed (without proof.)
Theorem CD-5.2
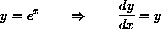
or, written in terms of the independent variable,
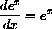
The derivative of the natural base logarithm is
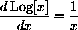
 base for logs and exponentials makes their calculus "natural."
base for logs and exponentials makes their calculus "natural."
 as x increases by h equals k times f[x]." as a mathematical equation.
In other words, your equation should say, "f[x] increases by
as x increases by h equals k times f[x]." as a mathematical equation.
In other words, your equation should say, "f[x] increases by
 as x increases by h."
as x increases by h."
Suppose algae cells in a warm pond double every 6 hours and at time t=0 (hrs) there is one cell.
How many cells are there in 6 hours? How many cells are there in 12 hours? How many in 18 hours?
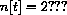
 , and the functional identity.
, and the functional identity.
 , write the increment approximation for
, write the increment approximation for
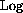 at x=1 to show that
at x=1 to show that
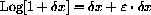
with
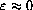 when
when
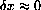 .
. 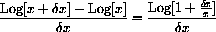

with
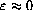 when
when
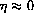 . Use these two facts to prove that for all positive x, bounded away from 0,
. Use these two facts to prove that for all positive x, bounded away from 0, 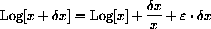
with
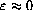 when
when
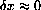 .
. 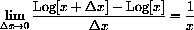
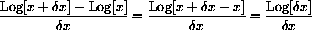
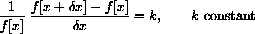
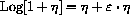 with
with
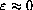 when
when
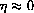 . Show that
. Show that
 when
when
 .
.  on the Computer Run the program DfctLimit to show graphically that the gap errors of
on the Computer Run the program DfctLimit to show graphically that the gap errors of
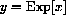 and
and
 tend to zero AS FUNCTIONS OF x for appropriate compact intervals
tend to zero AS FUNCTIONS OF x for appropriate compact intervals
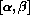 . (HINT: Where are the functions and their derivatives defined?)
. (HINT: Where are the functions and their derivatives defined?)
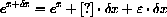
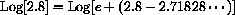 .
. Section Summary
This section shows that locally linear implies continuous and uniform derivatives are continuous.
Definition: A real function f[x] is continuous at the real point a if f[a] is defined and
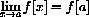
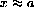 , f[x] is defined and
, f[x] is defined and
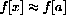
Theorem CD-5.3
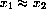 then
then
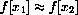 . Take x=x1 and
. Take x=x1 and
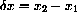 and use the approximation
and use the approximation
 where
where
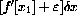 is medium times small = small, so
is medium times small = small, so
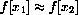 . That is the algebraic proof.
Draw the picture on a small scale.
. That is the algebraic proof.
Draw the picture on a small scale.
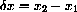 and use the approximation
and use the approximation
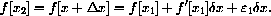
Next let x=x2, 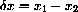 and use the approximation
and use the approximation
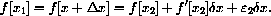
The different x-increments are negatives, so we have
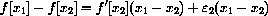
and
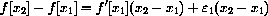
Adding, we obtain
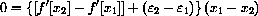
Dividing by the non-zero (x1-x2), we see that
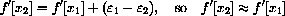
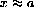 so that
so that
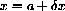 for
for
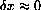 . Show that
. Show that
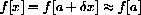 ; in other words, show that smooth real functions are continuous at real points.
; in other words, show that smooth real functions are continuous at real points. 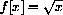 is defined for
is defined for
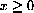 ; there is nothing wrong with f[0]. However, our increment computation for
; there is nothing wrong with f[0]. However, our increment computation for
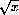 above was not valid at x=0 because a microscopic view of the graph focused at x=0 looks like a vertical ray (or half-line). Explain why this is so, but show that f[x] is still continuous "from the right;" that is, if
above was not valid at x=0 because a microscopic view of the graph focused at x=0 looks like a vertical ray (or half-line). Explain why this is so, but show that f[x] is still continuous "from the right;" that is, if
 , then
, then
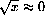 but
but
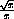 is very large.
is very large.
5.6.1
5.6.2
5.6.3