XLISP-STAT includes two functions for maximizing functions of several variables. The definitions needed are in the file maximize.lsp on the distribution disk. This file is not loaded automatically at start up; you should load it now, using the Load item on the File menu or the load command, to carry out the calculations in this section. The material in this section is somewhat more advanced as it assumes you are familiar with the basic concepts of maximum likelihood estimation.
Two functions are available for maximization. The first is newtonmax , which takes a function and a list or vector representing an initial guess for the location of the maximum and attempts to find the maximum using an algorithm based on Newton's method with backtracking. The algorithm is based on the unconstrained minimization system described in Dennis and Schnabel [10].
As an example, Cox and Snell [9, Example T,] describe data collected on times (in operating hours) between failures of air conditioning units on several aircraft. The data for one of the aircraft can be entered as
(def x (90 10 60 186 61 49 14 24 56 20 79 84 44 59 29 118 25 156 310 76
26 44 23 62 130 208 70 101 208))
A simple model for these data might be to assume the times between
failures are independent random variables with a common gamma
distribution. The density of the gamma distribution can be written as
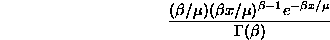
where 
is the mean time between failures and 
is the gamma
shape parameter. The log likelihood for the sample is thus given by
We can define a Lisp function to evaluate this log likelihood by
(defun gllik (theta)
(let* ((mu (select theta 0))
(beta (select theta 1))
(n (length x))
(bym (* x (/ beta mu))))
(+ (* n (- (log beta) (log mu) (log-gamma beta)))
(sum (* (- beta 1) (log bym)))
(sum (- bym)))))
This definition uses the function log-gamma to evaluate
. The data and function definition are contained
in the file aircraft.lsp in the Data folder of the
distribution disk.
Closed form maximum likelihood estimates are not available for the
shape parameter of this distribution, but we can use newtonmax
to compute estimates numerically.
We need an initial guess to use as a starting value in the
maximization. To get initial estimates we can compute the mean and
standard deviation of x
> (mean x) 83.5172 > (standard-deviation x) 70.8059and use method of moments estimates
and
, calculated as
> (^ (/ (mean x) (standard-deviation x)) 2) 1.39128Using these starting values we can now maximize the log likelihood function:
> (newtonmax #'gllik (list 83.5 1.4)) maximizing... Iteration 0. Criterion value = -155.603 Iteration 1. Criterion value = -155.354 Iteration 2. Criterion value = -155.347 Iteration 3. Criterion value = -155.347 Reason for termination: gradient size is less than gradient tolerance. (83.5173 1.67099)Some status information is printed as the optimization proceeds. You can turn this off by supplying the keyword argument :verbose with value NIL.
You might want to check that the gradient of the function is indeed close to zero. If you do not have a closed form expression for the gradient you can use numgrad to calculate a numerical approximation. For our example,
> (numgrad #'gllik (list 83.5173 1.67099)) (-4.07269e-07 -1.25755e-05)The elements of the gradient are indeed quite close to zero. You can also compute the second derivative, or Hessian, matrix using numhess . Approximate standard errors of the maximum likelihood estimates are given by the square roots of the diagonal entries of the inverse of the negative Hessian matrix at the maximum:
> (sqrt (diagonal (inverse (- (numhess #'gllik (list 83.5173 1.67099)))))) (11.9976 0.402648)
Instead of calculating the maximum using newtonmax and then
calculating the derivatives separately you can have newtonmax
return a list of the location of the maximum, the optimal function
value, the gradient and the Hessian by supplying the keyword argument
:return-derivs as T.
Newton's method assumes a function is twice continuously differentiable. If your function is not smooth or you are having trouble with newtonmax for some other reason you might try a second maximization function, nelmeadmax . nelmeadmax takes a function and an initial guess and attempts to find the maximum using the Nelder-Mead simplex method as described in Press, Flannery, Teukolsky and Vetterling [14]. The initial guess can consist of a simplex, a list of n+1 points for an n-dimensional problem, or it can be a single point, represented by a list or vector of n numbers. If you specify a single point you should also use the keyword argument :size to specify as a list or vector of length n the size in each dimension of the initial simplex. This should represent the size of an initial range in which the algorithm is to start its search for a maximum. We can use this method in our gamma example:
> (nelmeadmax #'gllik (list 83.5 1.4) :size (list 5 .2)) Value = -155.603 Value = -155.603 Value = -155.603 Value = -155.587 Value = -155.53 Value = -155.522 ... Value = -155.347 Value = -155.347 Value = -155.347 Value = -155.347 (83.5181 1.6709)It takes somewhat longer than Newton's method but it does reach the same result.