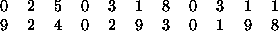
Statistical data usually consists of groups of numbers. Devore and Peck [11, Exercise 2.11,] describe an experiment in which 22 consumers reported the number of times they had purchased a product during the previous 48 week period. The results are given as a table:
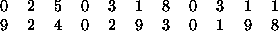
To examine this data in XLISP-STAT we represent it as a list of numbers using the list function:
> (list 0 2 5 0 3 1 8 0 3 1 1 9 2 4 0 2 9 3 0 1 9 8) (0 2 5 0 3 1 8 0 3 1 1 9 2 4 0 2 9 3 0 1 9 8) >Note that the numbers are separated by white space (spaces, tabs or even returns), not commas.
The mean function can be used to compute the average of a list of numbers. We can combine it with the list function to find the average number of purchases for our sample:
> (mean (list 0 2 5 0 3 1 8 0 3 1 1 9 2 4 0 2 9 3 0 1 9 8)) 3.227273 >The median of these numbers can be computed as
> (median (list 0 2 5 0 3 1 8 0 3 1 1 9 2 4 0 2 9 3 0 1 9 8)) 2 >
It is of course a nuisance to have to type in the list of 22 numbers
every time we want to compute a statistic for the sample. To avoid
having to do this I will give this list a name using the
def special form
![]() :
:
> (def purchases (list 0 2 5 0 3 1 8 0 3 1 1 9 2 4 0 2 9 3 0 1 9 8)) PURCHASES >Now the symbol purchases has a value associated with it: Its value is our list of 22 numbers. If you give the symbol purchases to the evaluator then it will find the value of this symbol and return that value:
> purchases (0 2 5 0 3 1 8 0 3 1 1 9 2 4 0 2 9 3 0 1 9 8) >We can now easily compute various numerical descriptive statistics for this data set:
> (mean purchases) 3.227273 > (median purchases) 2 > (standard-deviation purchases) 3.279544 > (interquartile-range purchases) 3.5 >
XLISP-STAT also supports elementwise arithmetic operations on lists of numbers. For example, we can add 1 to each of the purchases:
> (+ 1 purchases) (1 3 6 1 4 2 9 1 4 2 2 10 3 5 1 3 10 4 1 2 10 9) >and after adding 1 we can compute the natural logarithms of the results:
> (log (+ 1 purchases)) (0 1.098612 1.791759 0 1.386294 0.6931472 2.197225 0 1.386294 0.6931472 0.6931472 2.302585 1.098612 1.609438 0 1.098612 2.302585 1.386294 0 0.6931472 2.302585 2.197225) >