Scalability
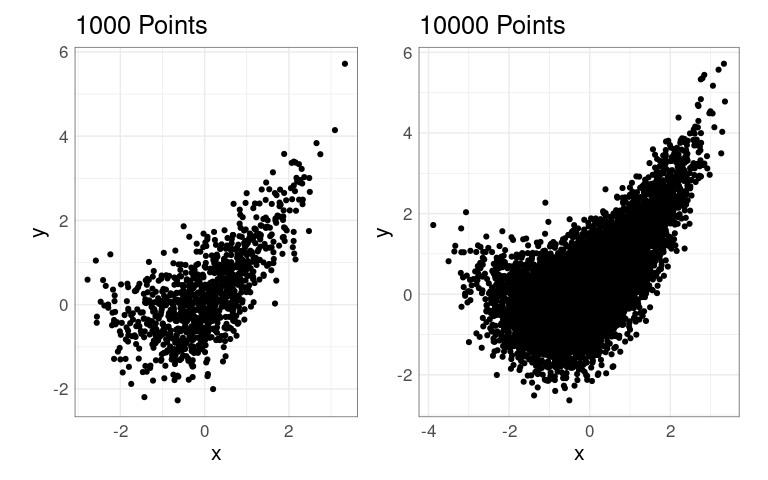
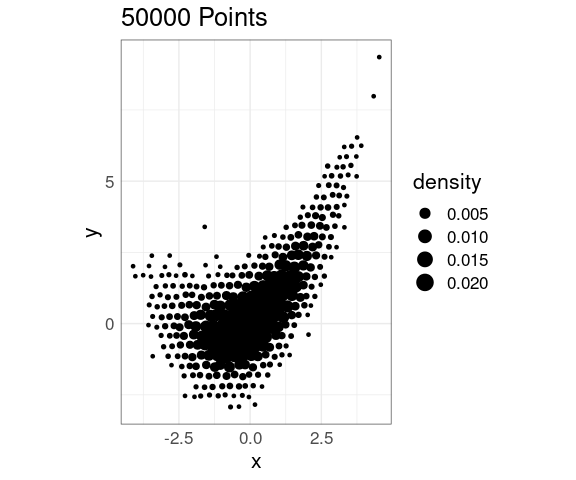
Scatter plots work well for hundreds of observations
Over-plotting becomes an issue once the number of observations gets into tens of thousands.
For some output formats storage also becomes an issue as the number of points plotted increases.
Some simulated data:
n <- 50000
## n50K <- data.frame(x = rnorm(n), y = rnorm(n))
x <- rnorm(n)
y <- x + 0.4 * x ^ 2 + rnorm(n)
y <- y / sd(y)
n50K <- data.frame(x = x, y = y)
n10K <- n50K[1 : 10000, ]
n1K <- n50K[1 : 1000, ]
p1 <- ggplot(n1K, aes(x, y)) +
geom_point() +
coord_equal() +
ggtitle(sprintf("%d Points", nrow(n1K)))
p2 <- ggplot(n10K, aes(x, y)) +
geom_point() +
coord_equal() +
ggtitle(sprintf("%d Points", nrow(n10K)))
library(patchwork)
p1 | p2
Some Simple Options
Simple options to address over-plotting:
sampling
reducing the point size
alpha blending
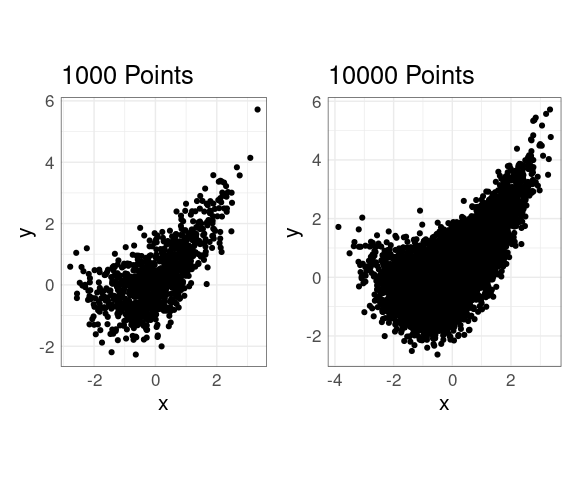
With no adjustments:
p2 + xlim(c(-5, 5)) + ylim(c(-3, 10))
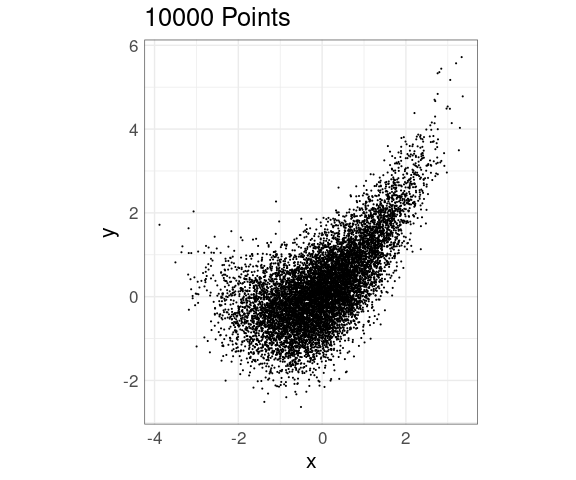
Reducing the point size helps when the number of points is in the low tens of thousands:
ggplot(n10K, aes(x, y)) +
geom_point(size = 0.1) +
coord_equal() +
xlim(c(-5, 5)) +
ylim(c(-3, 10)) +
ggtitle(sprintf("%d Points", nrow(n10K)))
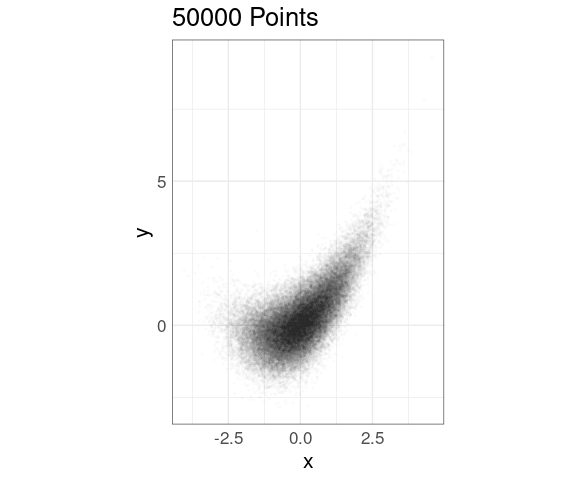
Alpha blending can also be effective, on its own or in combination with point size adjustment:
ggplot(n50K, aes(x, y)) +
geom_point(alpha = 0.01, size = 0.5) +
coord_equal() +
xlim(c(-5, 5)) +
ylim(c(-3, 10)) +
ggtitle(sprintf("%d Points", nrow(n50K)))
Experimentation is usually needed to identify a good point size and alpha level.
Both alpha blending and point size reduction inhibit the use of color for encoding a grouping variable.
The best choices may vary from one output format to another.
Density Estimation Methods
Some methods based on density estimation or binning:
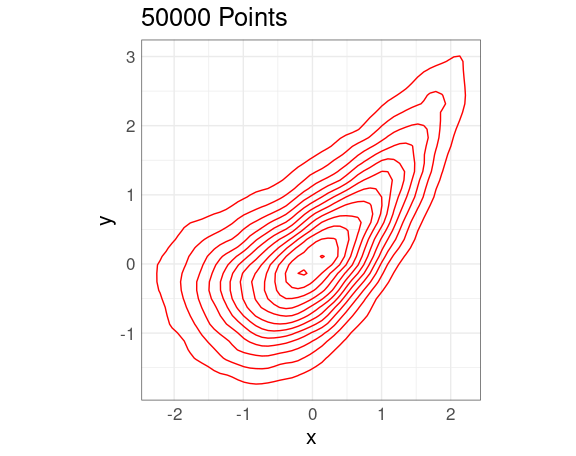
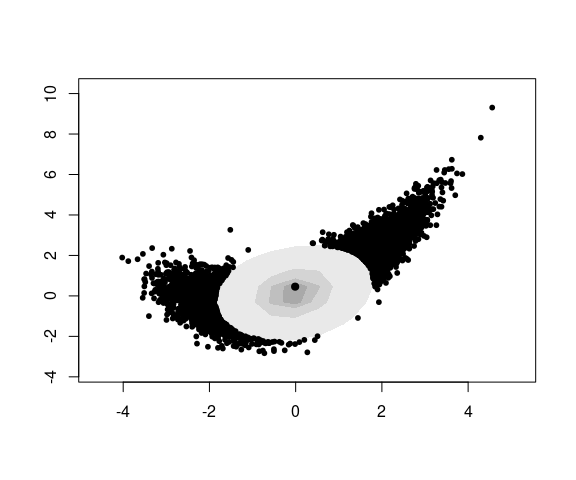
Density Contours
A 2D density estimate can be displayed in terms of its contours , or level curves .
p <- ggplot(n50K, aes(x, y)) +
coord_equal() +
ggtitle(sprintf("%d Points", nrow(n50K)))
pp <- geom_point(alpha = 0.01, size = 0.5)
dd <- geom_density_2d(color = "red")
p + dd
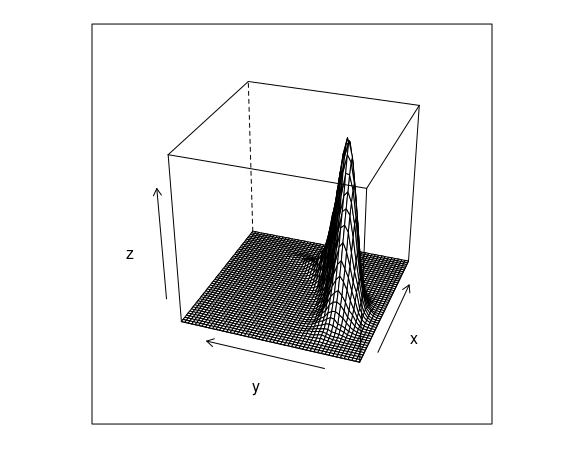
These are the contours of the estimated density surface:
d <- MASS::kde2d(n50K$x, n50K$y, n = 50)
v <- expand.grid(x = d$x, y = d$y)
v$z <- as.numeric(d$z)
lattice::wireframe(z ~ x + y,
data = v,
screen = list(z = 70,
x = -60))
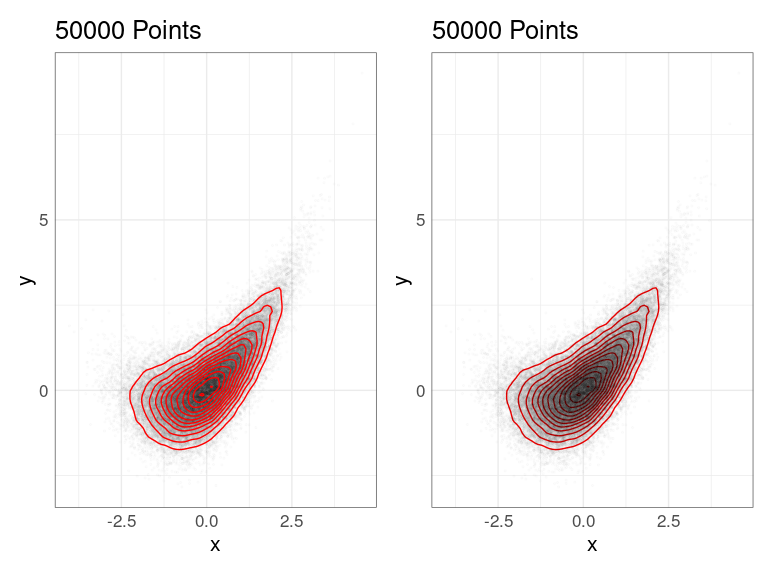
2D density estimate contours can be superimposed on a set of points or placed beneath a set of points:
p1 <- p + list(pp, dd)
p2 <- p + list(dd, pp)
p1 | p2
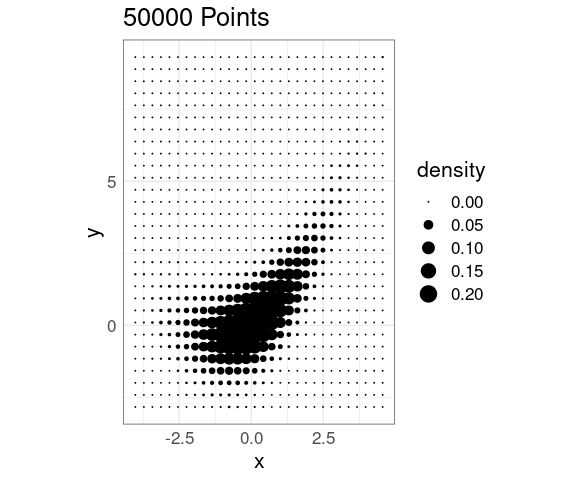
Density Levels Encoded with Point Size
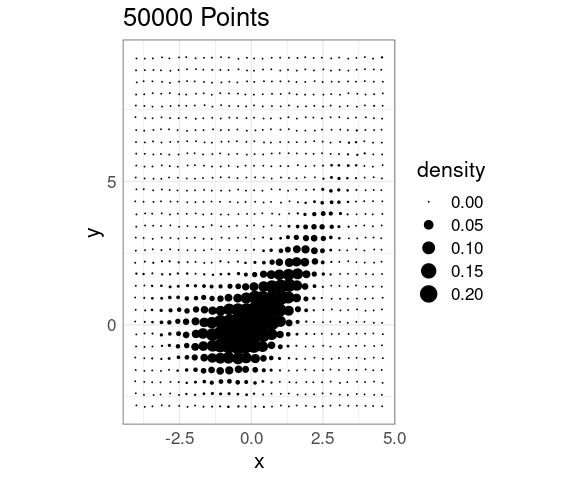
Density levels can also be encoded in point size in a grid of points:
p + stat_density_2d(
aes(size = after_stat(density)),
geom = "point",
n = 30,
contour = FALSE) +
scale_size(range = c(0, 6))
This scales well computationally
It does not easily support encoding a grouping with color or shape.
It introduces some distracting visual artifacts that are related to some optical illusions seen earlier .
This effect can be reduced somewhat by jittering:
jit_amt <- 0.03
p + stat_density_2d(
aes(size = after_stat(density)),
geom = "point",
position = position_jitter(jit_amt,
jit_amt),
n = 30, contour = FALSE) +
scale_size(range = c(0, 6))
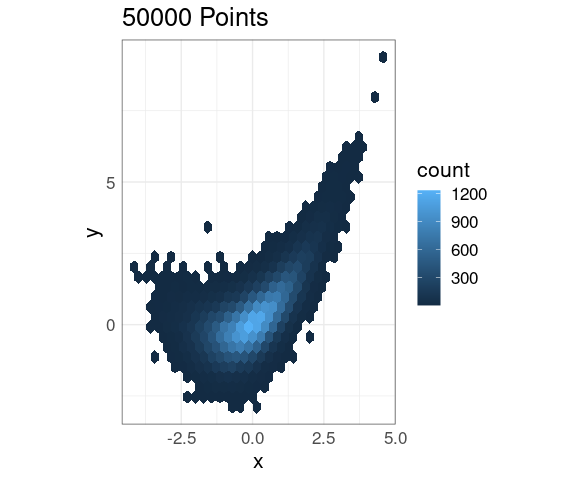
Hexagonal Binning
Hexagonal binning divides the plane into hexagonal bins and displays the number of points in each bin:
p + geom_hex()
This also scales very well to larger data sets.
The default color scheme seems less than ideal.
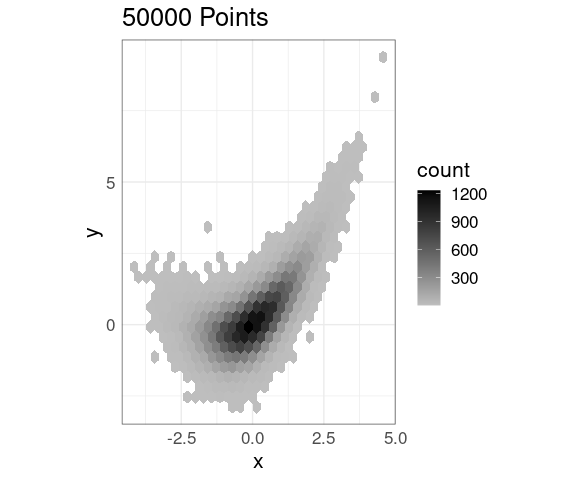
An alternative fill color choice:
p + geom_hex() +
scale_fill_gradient(low = "gray",
high = "black")
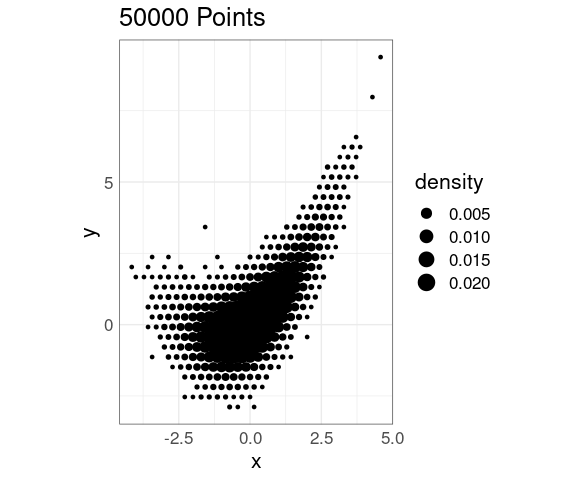
Again it is possible to use a scaled point representation:
p + stat_bin_hex(
geom = "point",
aes(size = after_stat(density)),
fill = NA)
This representation still produces some visual distractions, but less than a rectangular grid.
Again, jittering can help:
jit_amt <- 0.05
p + stat_bin_hex(
aes(size = after_stat(density)),
geom = "point",
position = position_jitter(jit_amt,
jit_amt),
fill = NA)
Other Density Plots
The hdrcde package computes and plots density contours containing specified proportions of the data.
The hdr.boxplot.2d function plots these contours and shows the points not in the outermost contour:
library(hdrcde)
with(n50K,
hdr.boxplot.2d(x, y,
prob = c(0.1, 0.5, 0.75, 0.9)))
Some Enhancements
Encoding Additional Variables
Scatter plots can encode information about other variables using
symbol color
symbol size
symbol shape
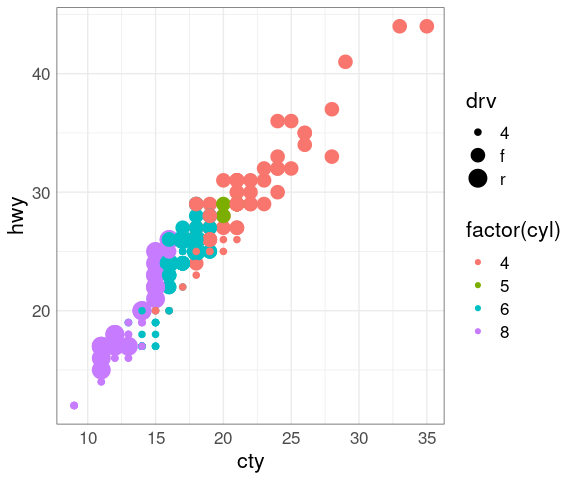
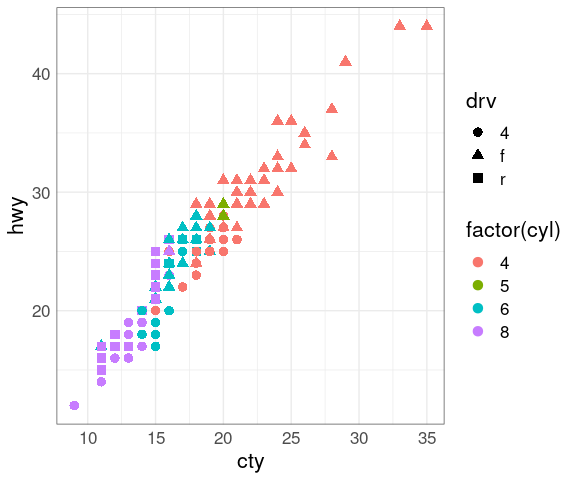
An example using the mpg data set:
p <- ggplot(mpg, aes(cty, hwy,
color = factor(cyl)))
p + geom_point(aes(size = drv))
## Warning: Using size for a discrete variable is not advised.
Some encodings work better than others:
Size is not a good fit for a discrete variable
Even though cyl is numeric, it is best encoded as categorical.
Size and color interfere with each other as the color of smaller objects is harder to perceive.
Similarly, size and shape interfere with each other.
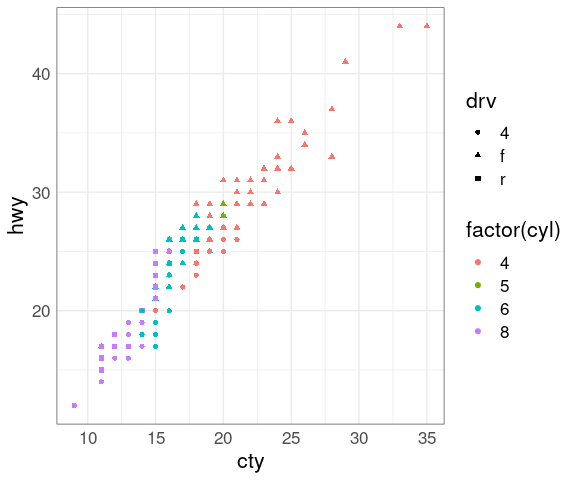
Using shape instead of size for drv:
p + geom_point(aes(shape = drv))
Increasing the size makes shapes and the colors easier to distinguish:
p + geom_point(aes(shape = drv), size = 3)
Marginal Plots
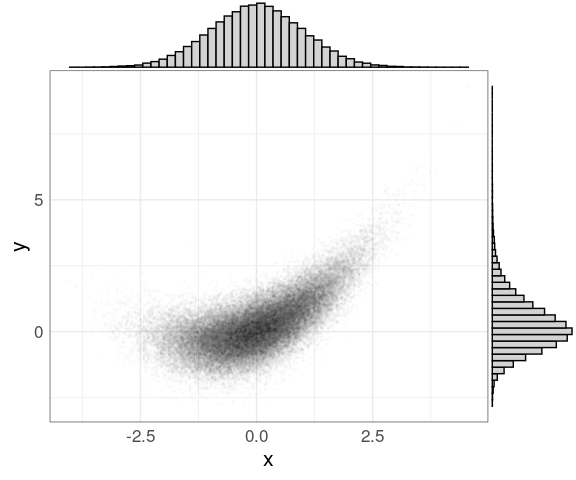
The ggMargin function in the ggExtra package attaches marginal histograms to (some) plots produced by ggplot:
library(ggExtra)
p <- ggplot(n50K, aes(x, y)) +
geom_point(alpha = 0.01, size = 0.5)
ggMarginal(p,
type = "histogram",
bins = 50,
fill = "lightgrey")
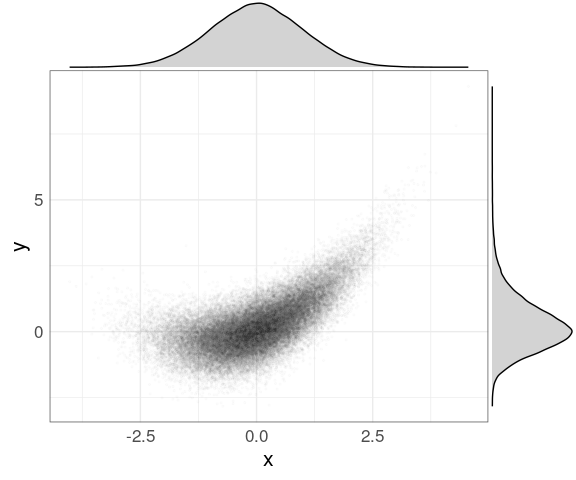
The default type is "density" for a marginal density plot:
ggMarginal(p, fill = "lightgrey")
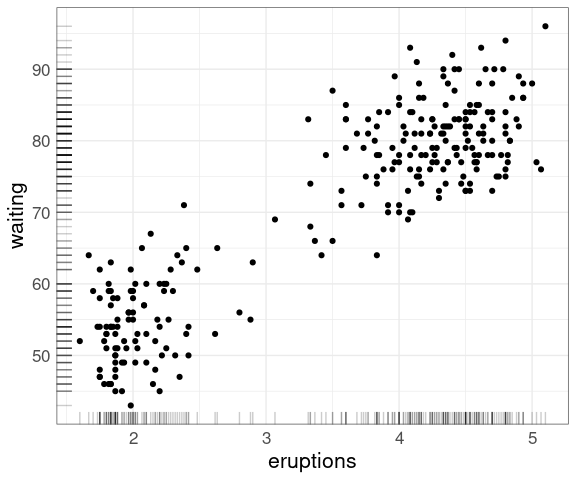
For data sets of more modest size rug plots along the axes can be useful:
ggplot(faithful,
aes(eruptions, waiting)) +
geom_point() +
geom_rug(alpha = 0.2)
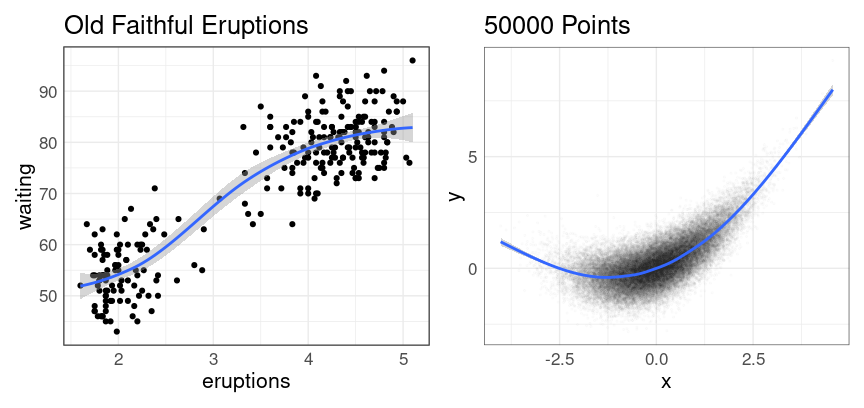
Adding a Smooth Curve
When the variables on the \(y\) axis is a response variable a useful enhancement is to add a smooth curve to a plot.
The default method is a form of local averaging, and includes a representation of uncertainty:
p1 <- ggplot(faithful, aes(eruptions, waiting)) +
geom_point() +
geom_smooth() +
ggtitle("Old Faithful Eruptions")
p2 <- ggplot(n50K, aes(x, y)) +
pp +
geom_smooth() +
ggtitle(sprintf("%d Points", nrow(n50K)))
p1 | p2
Conditioning
When the \(y\) variable is a response it can also be useful to explore the conditional distribution of \(y\) given different values of the \(x\) variable.
One way to do this is to focus on the data for narrow ranges of the conditioning variable.
Two approaches for creating groups to focus on:
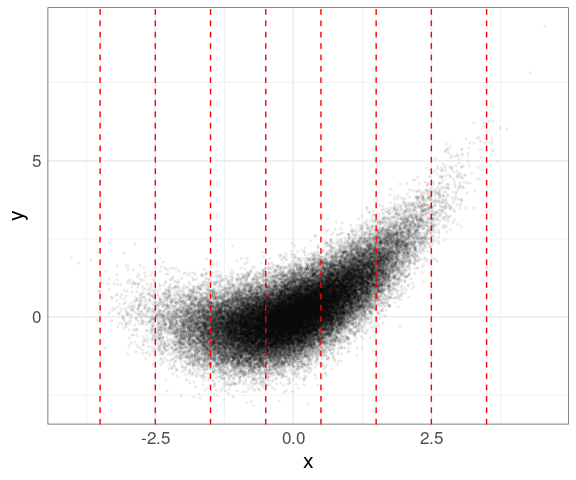
Rounding to an integer or using
cut_width(x, width = 1, center = 0)produces these bins:
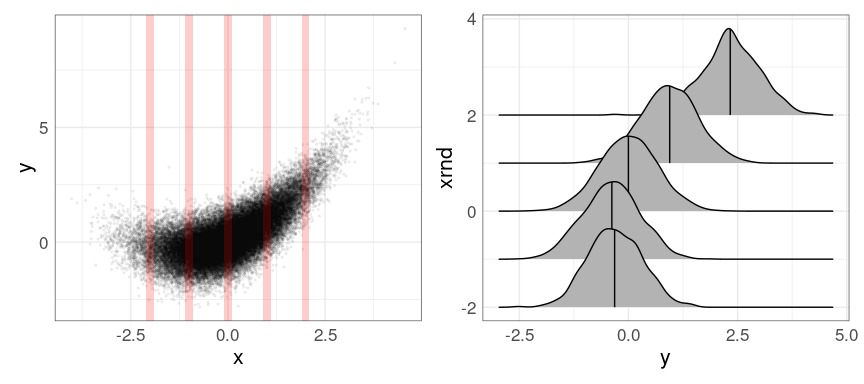
p <- ggplot(n50K, aes(x, y)) +
geom_point(alpha = 0.05, size = 0.5)
p + geom_vline(xintercept =
seq(-3.5, 4.5, by = 1),
linetype = 2,
color = "red") +
scale_x_continuous(breaks = seq(-3, 4),
labels = as.character(seq(-3, 4)))
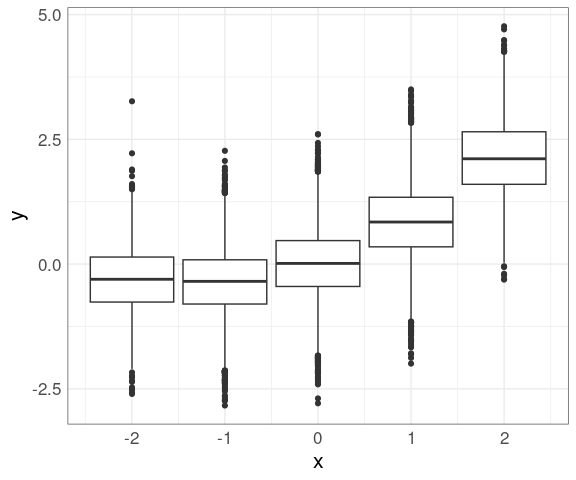
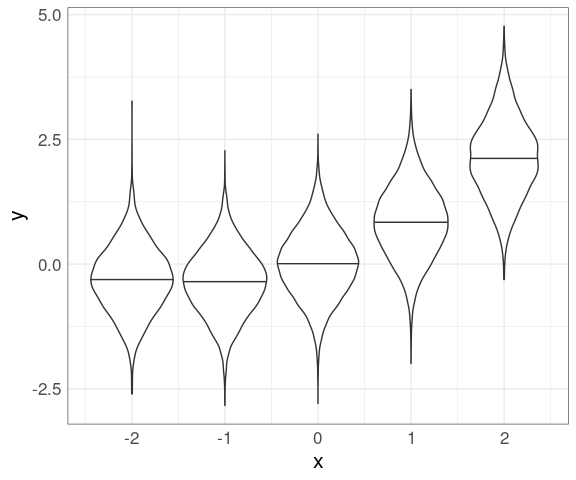
Data within each group can then be shown using box plots (you need to use the group aesthetic to plot on a continuous axis):
n50K_trm <- filter(n50K, x > -2.5, x < 2.5)
mutate(n50K_trm, xrnd = round(x)) |>
ggplot(aes(x, y)) +
geom_boxplot(aes(group = xrnd))
Using cut_width and violin plots:
mutate(n50K_trm,
xcut = cut_width(x,
width = 1,
center = 0)) |>
group_by(xcut) |>
mutate(xmed = median(x)) |>
ungroup() |>
ggplot(aes(x, y)) +
geom_violin(aes(group = xmed),
draw_quantiles = 0.5)
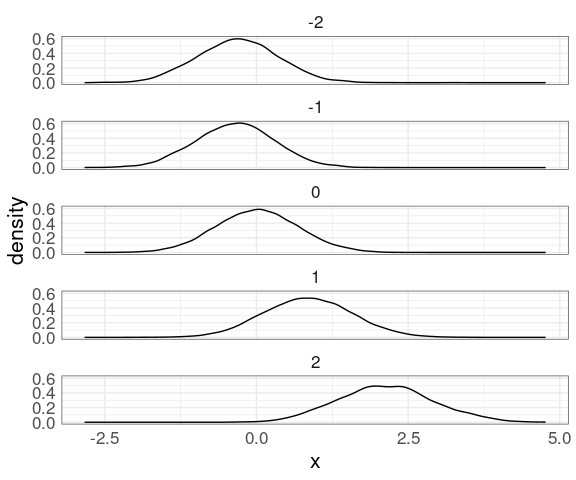
Another option for visualizing the conditional distributions is faceted density plots:
mutate(n50K_trm, xrnd = round(x)) |>
ggplot(aes(x)) +
geom_density(aes(y)) +
facet_wrap(~ xrnd, ncol = 1)
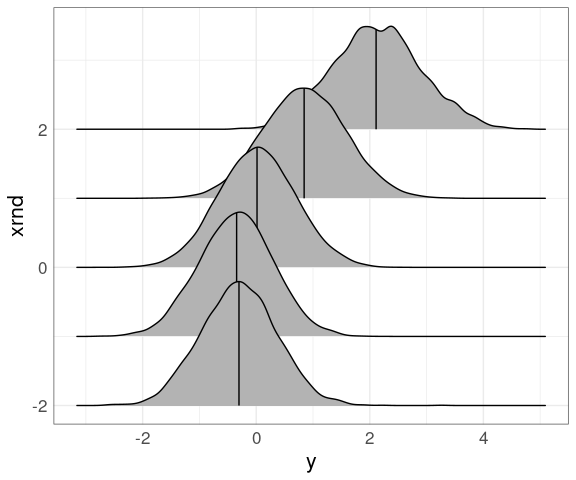
Density ridges work as well:
library(ggridges)
mutate(n50K_trm, xrnd = round(x)) |>
ggplot(aes(y, xrnd, group = xrnd)) +
geom_density_ridges(quantile_lines = TRUE,
quantiles = 2)
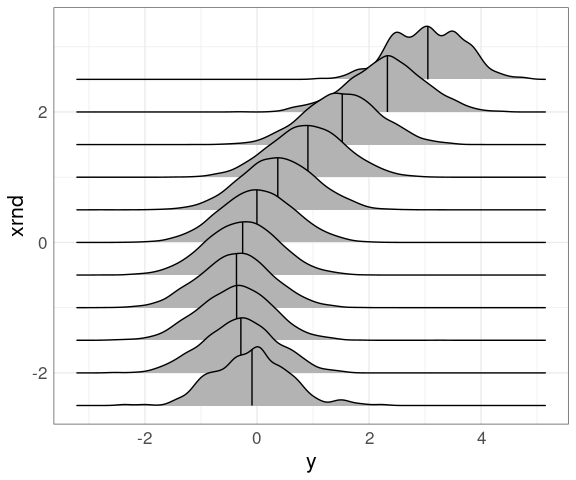
Using a larger set of narrower bins centered on multiples of 1/2:
mutate(n50K_trm, xrnd = round(2 * x) / 2) |>
ggplot(aes(y, xrnd, group = xrnd)) +
geom_density_ridges(quantile_lines = TRUE,
quantiles = 2)
Sometimes it is useful to use a small number of narrow bins:
rdata <- data.frame(xmin = (-2 : 2) - 0.1,
xmax = (-2 : 2) + 0.1,
ymin = -Inf,
ymax = Inf)
p1 <- p + geom_rect(aes(xmin = xmin, xmax = xmax, ymin = ymin, ymax = ymax),
data = rdata,
inherit.aes = FALSE,
fill = "red",
alpha = 0.2)
p2 <- mutate(n50K_trm, xrnd = round(x)) |>
filter(abs(x - xrnd) < 0.1) |>
ggplot(aes(y, xrnd, group = xrnd)) +
geom_density_ridges(quantile_lines = TRUE, quantiles = 2)
p1 | p2
For examining conditional distributions, bins need to be:
For smaller data sets it can also be useful to allow bins to overlap.
The lattice functions shingle and equal.count create shingles that can be used in lattice-style faceting.
Example: Diamond Prices
The diamonds data set contains prices and other attributes for 53,940 diamonds.
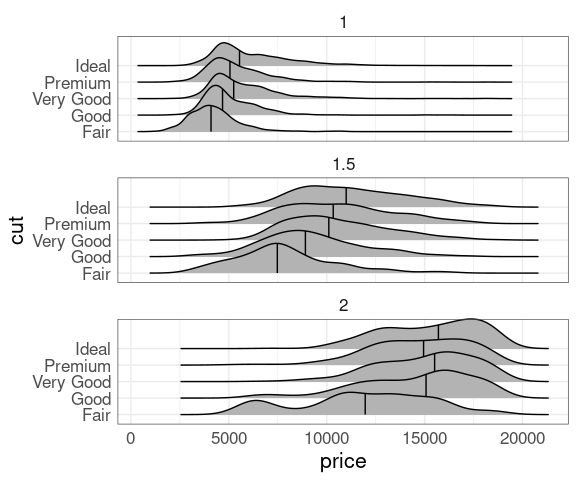
The cut variable indicates the quality of a diamond’s cut.
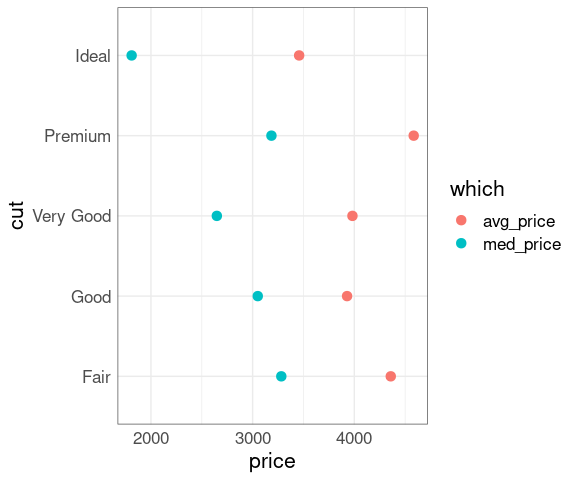
You might expect ‘better’ cuts to cost more, but that is not true on average:
mm <- group_by(diamonds, cut) |>
summarize(med_price = median(price),
avg_price = mean(price),
n = length(price)) |>
pivot_longer(2 : 3,
names_to = "which",
values_to = "price")
ggplot(mm, aes(x = price,
y = cut,
color = which)) +
geom_point(, size = 3)
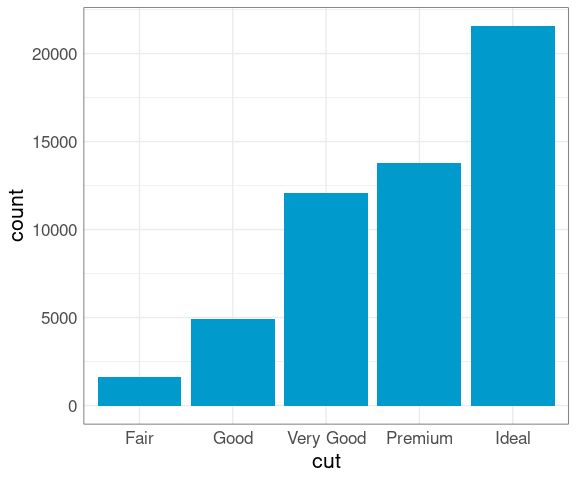
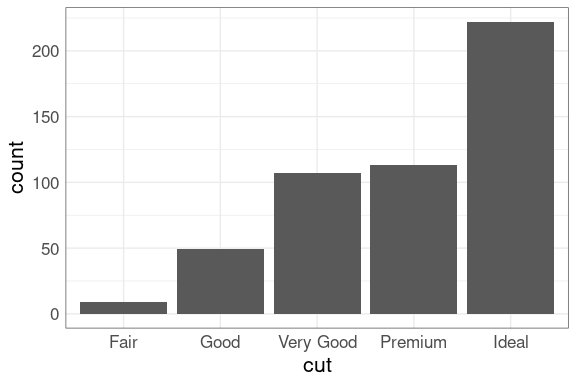
The proportion of diamonds at each cut level is also perhaps surprising:
ggplot(diamonds) +
geom_bar(aes(x = cut),
fill = "deepskyblue3")
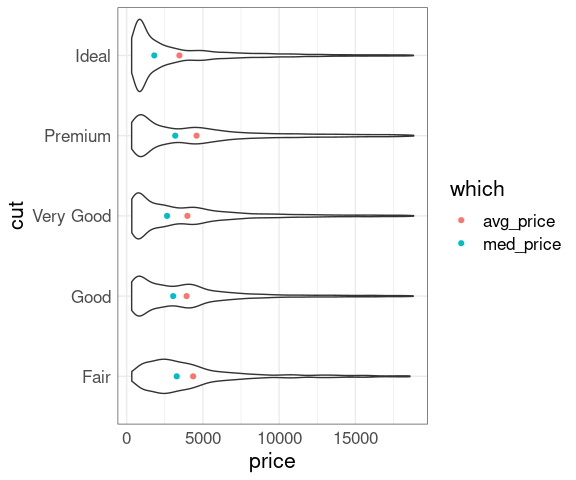
And the price distributions within each cut level differ in shape:
ggplot(diamonds, aes(x = price, y = cut)) +
geom_violin() +
geom_point(aes(color = which), data = mm)
Another important factor is the size, measured in carat.
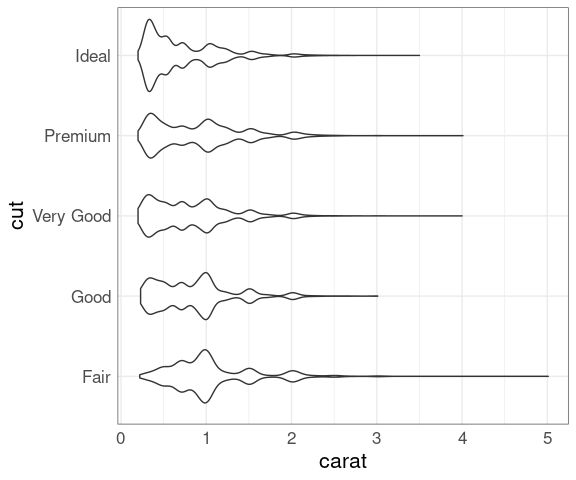
ggplot(diamonds, aes(x = carat, y = cut)) +
geom_violin()
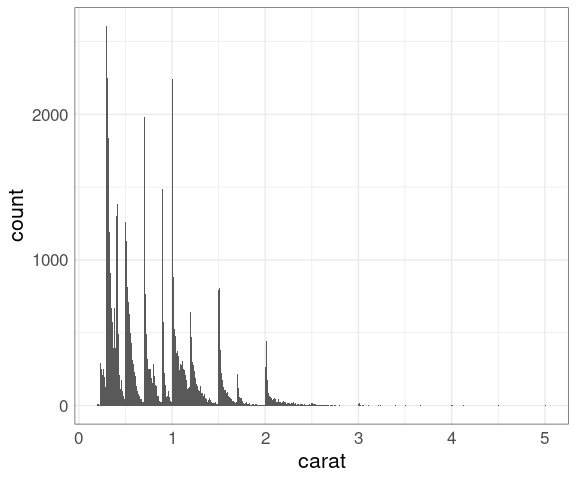
Histograms with a narrow bin width may help understand the unusual shapes.
ggplot(diamonds) +
geom_histogram(aes(carat),
binwidth = 0.01)
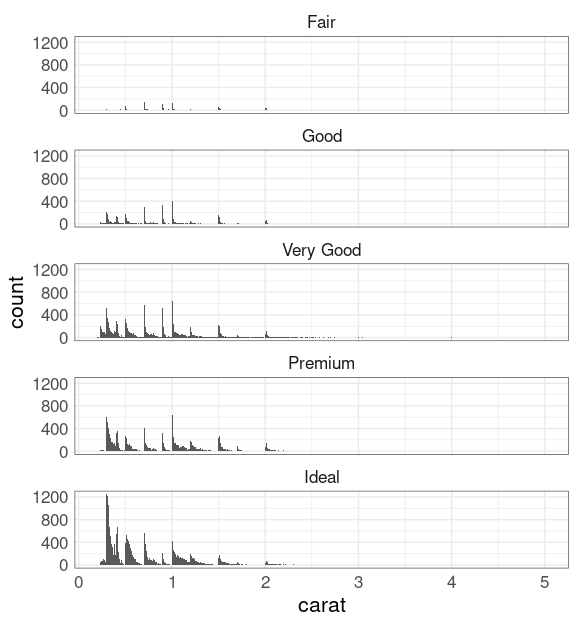
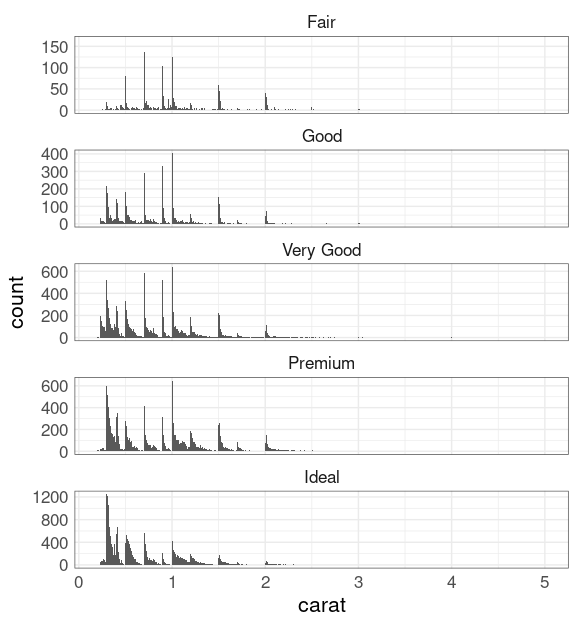
Try faceting on cut:
ggplot(diamonds) +
geom_histogram(aes(carat),
binwidth = 0.01) +
facet_wrap(~ cut, ncol = 1)
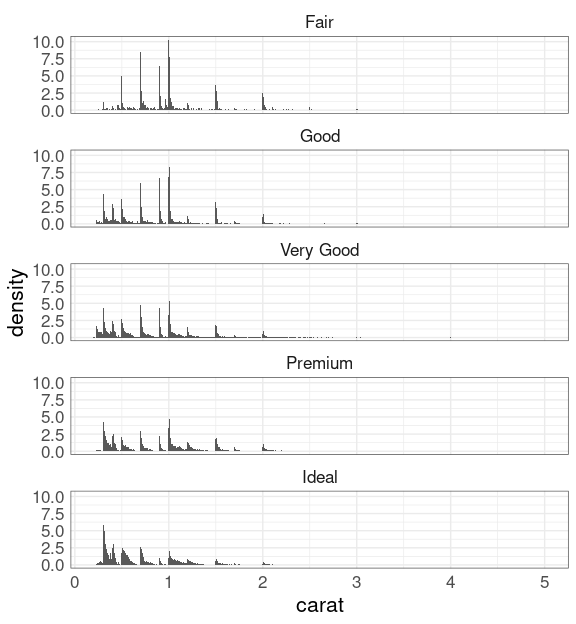
To focus on the shapes of the conditional distributions of carat given cut use y = after_stat(density):
ggplot(diamonds) +
geom_histogram(
aes(x = carat,
y = after_stat(density)),
binwidth = 0.01) +
facet_wrap(~ cut, ncol = 1)
Alternatively, you can facet with scales = "free_y":
ggplot(diamonds) +
geom_histogram(aes(carat),
binwidth = 0.01) +
facet_wrap(~ cut,
scales = "free_y",
ncol = 1)
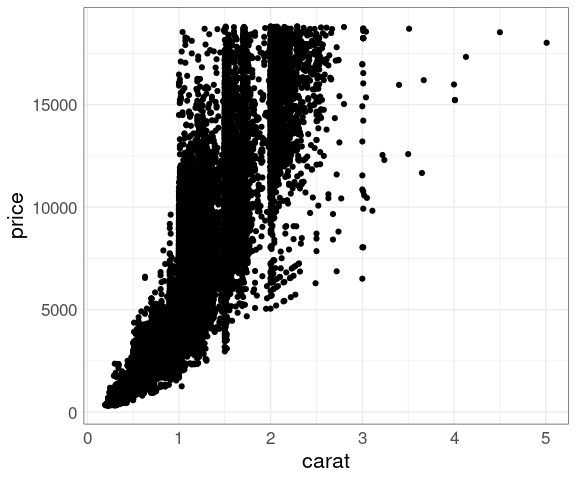
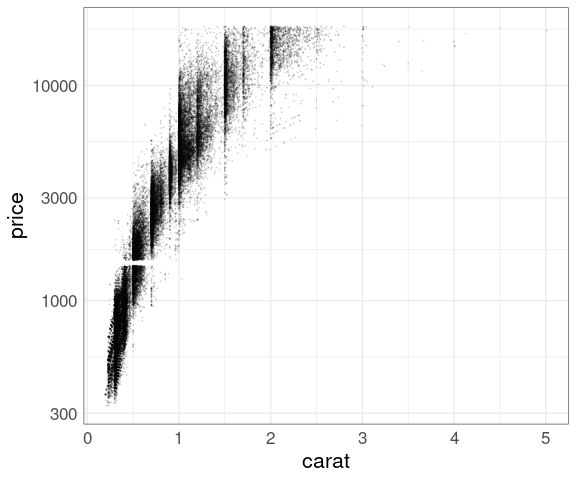
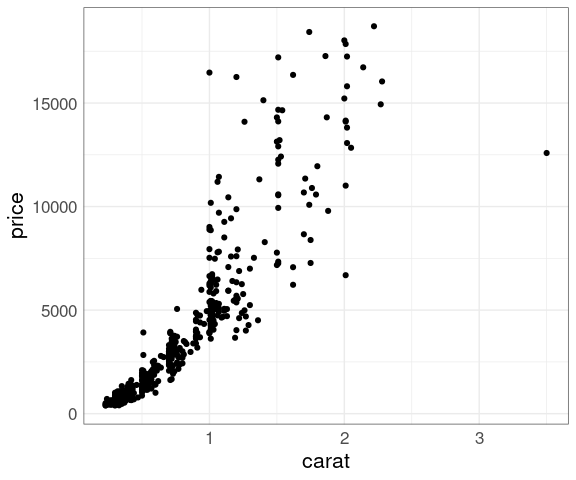
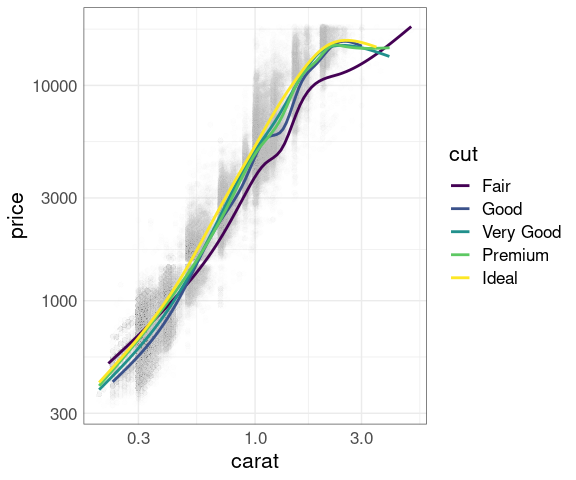
Larger diamonds have a higher price:
ggplot(diamonds, aes(x = carat, y = price)) +
geom_point()
There is a lot of over-plotting, so a good opportunity to try some of the techniques we have learned.
Some explorations:
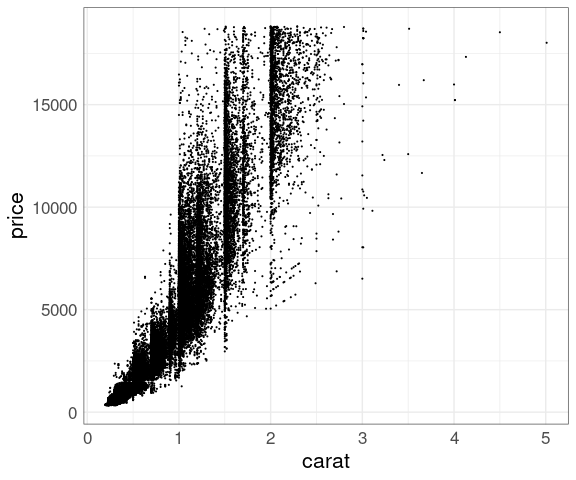
Reduced point size:
p <- ggplot(diamonds,
aes(x = carat, y = price))
p + geom_point(size = 0.1)
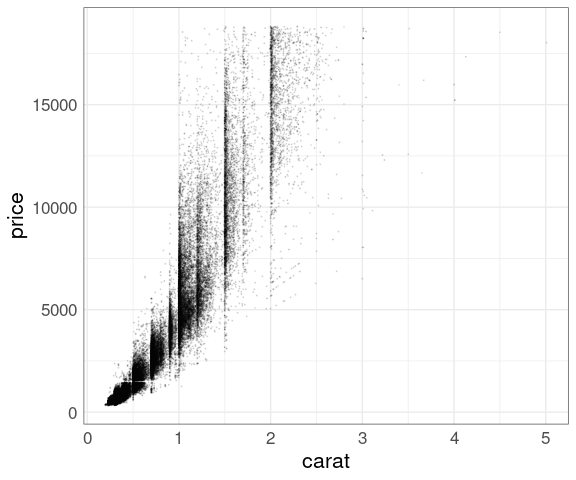
Reduced point size and alpha level:
p + geom_point(size = 0.1, alpha = 0.1)
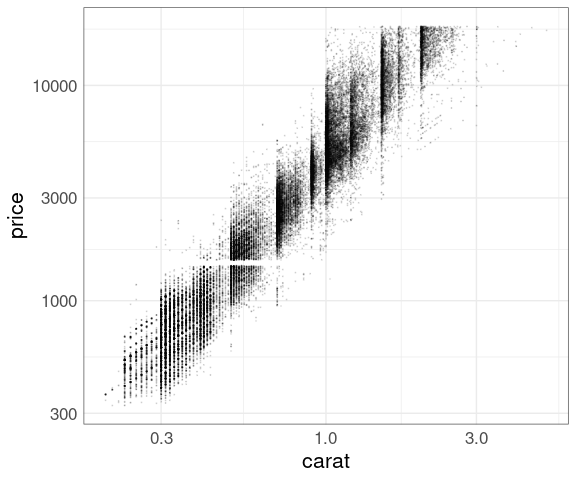
Try log scale for price:
p + geom_point(size = 0.1, alpha = 0.1) +
scale_y_log10()
Log scale for both:
p + geom_point(size = 0.1, alpha = 0.1) +
scale_x_log10() +
scale_y_log10()
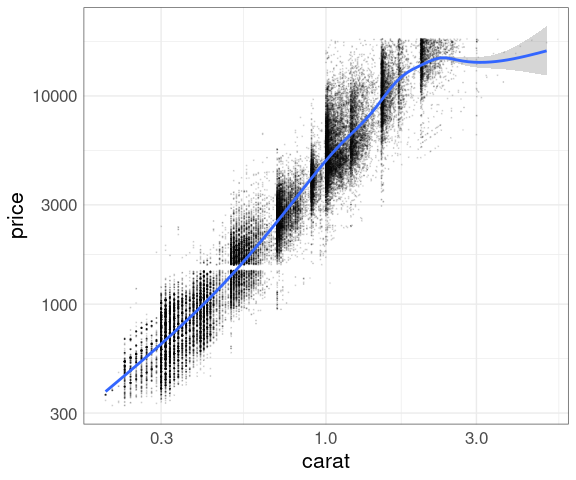
Add a smooth:
p + geom_point(size = 0.1, alpha = 0.1) +
geom_smooth() +
scale_x_log10() +
scale_y_log10()
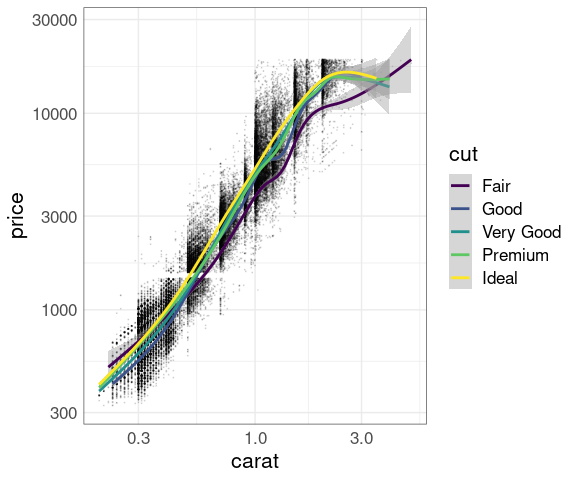
Separate smooths for each cut:
p + geom_point(size = 0.1, alpha = 0.1) +
geom_smooth(aes(color = cut)) +
scale_x_log10() +
scale_y_log10()
Exploring a sample:
d500 <- sample_n(diamonds, 500)Distribution of cut in the sample:
ggplot(d500, aes(x = cut)) +
geom_bar()
ggplot(d500, aes(x = carat, y = price)) +
geom_point()
You can also take a stratified sample stratified on cut using group_by, sample_frac, and ungroup.
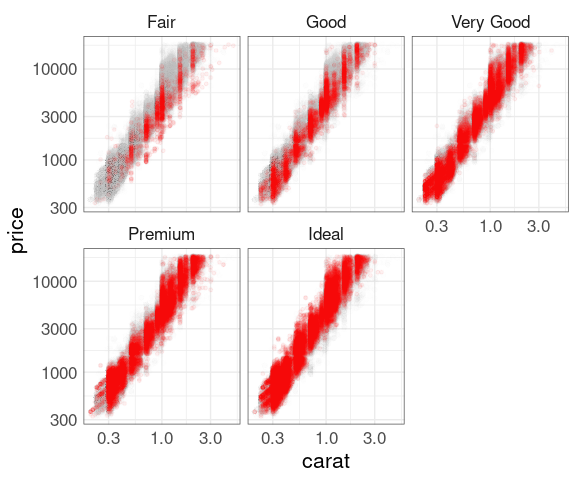
Explorations using facets:
p0 <- ggplot(diamonds, aes(x = carat, y = price))
dNoCut <- mutate(diamonds, cut = NULL)
p1 <- p0 + geom_point(alpha = 0.01, color = "grey", data = dNoCut)
p <- p1 + geom_point(color = "red", size = 1, alpha = 0.05)
## p + facet_wrap(~ cut)
p + facet_wrap(~ cut) + scale_x_log10() + scale_y_log10()
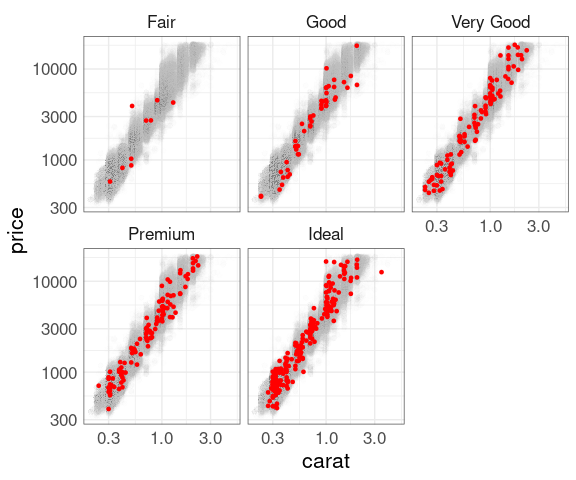
Facets with a sample:
p500 <- p1 +
geom_point(data = d500,
color = "red",
size = 1)
## p500
## p500 + facet_wrap(~ cut)
p500 +
facet_wrap(~ cut) +
scale_x_log10() +
scale_y_log10()
Muted data with smooths:
p1 +
geom_smooth(aes(color = cut),
se = FALSE) +
scale_x_log10() +
scale_y_log10()
Conditioning, carat values near 1, 1.5, or 2:
drnd <- mutate(diamonds,
crnd = round(2 * carat) / 2)
## Look at a bar chart of count(drnd, crnd)
## Drop higher carat values from density ridges
## map cut to color or fill (need to use group = interaction(crnd, cut))
## try log scale for price
filter(drnd,
crnd <= 2, crnd >= 1,
carat >= crnd, carat <= crnd + 0.1) |>
ggplot(aes(x = price, y = cut)) +
geom_density_ridges(quantile_lines = TRUE,
quantiles = 2) +
facet_wrap(~crnd, ncol = 1)
Exercises
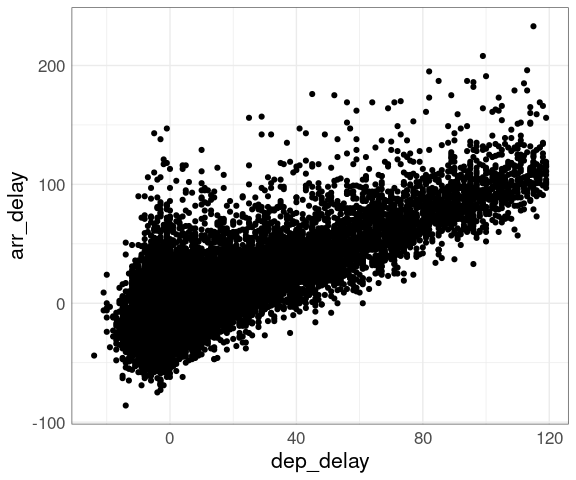
A plot of arrival delay against departure delay for the NYC flight data shows a lot of over-plotting, even for a 10% sample.
library(dplyr)
library(ggplot2)
library(nycflights13)
fl <- filter(flights, dep_delay < 120) |>
sample_frac(0.1)
p <- ggplot(fl, aes(x = dep_delay, arr_delay)) +
geom_point()
p
## Warning: Removed 101 rows containing missing values or values outside the scale range
## (`geom_point()`).
This masks the fact that three quarters of the flights in this sample have departure delays of less than 10 minutes. Superimposing density contours is one way to address this issue.
Which of the following adds four red density contours to the plot?
p + geom_density_2d(color = "red")p + geom_density_2d(bins = 4, color = "red")p + geom_hex(bins = 5)p + geom_density_2d(bins = 5) The diamonds data set is large enough for a scatter plot of price against carat to suffer from a significant amount of over-plotting. With p created as
library(ggplot2)
p <- ggplot(diamonds, aes(x = carat, y = price))which of the following is the best choice to address the over-plotting issue?
p + geom_point()p + geom_point(size = 0.5)p + geom_point(size = 0.1, alpha = 0.1)p + geom_point(position = "jitter") Consider the code
library(dplyr)
library(ggplot2)
filter(diamonds, carat < 3) |>
mutate(crnd = round(carat)) |>
filter(---) |>
ggplot(aes(x = price, y = crnd, group = crnd)) +
geom_density_ridges()Which replacement for --- produces a plot showing the conditional density of price given carat for carat values near one and the conditional density of price given carat for carat values near two?
abs(carat - crnd) < 0.1carat < 0.1abs(crnd) < 1carat + crnd < 2
LS0tCnRpdGxlOiAiU2NhdHRlciBQbG90IFNjYWxhYmlsaXR5IGFuZCBFbmhhbmNlbWVudHMiCm91dHB1dDoKICBodG1sX2RvY3VtZW50OgogICAgdG9jOiB5ZXMKICAgIGNvZGVfZm9sZGluZzogc2hvdwogICAgY29kZV9kb3dubG9hZDogdHJ1ZQotLS0KCjxsaW5rIHJlbD0ic3R5bGVzaGVldCIgaHJlZj0ic3RhdDQ1ODAuY3NzIiB0eXBlPSJ0ZXh0L2NzcyIgLz4KPHN0eWxlIHR5cGU9InRleHQvY3NzIj4gLnJlbWFyay1jb2RlIHsgZm9udC1zaXplOiA4NSU7IH0gPC9zdHlsZT4KPCEtLSB0aXRsZSBiYXNlZCBvbiBXaWxrZSdzIGNoYXB0ZXIgLS0+CgpgYGB7ciBzZXR1cCwgaW5jbHVkZSA9IEZBTFNFLCBtZXNzYWdlID0gRkFMU0V9CnNvdXJjZShoZXJlOjpoZXJlKCJzZXR1cC5SIikpCmtuaXRyOjpvcHRzX2NodW5rJHNldChjb2xsYXBzZSA9IFRSVUUsIG1lc3NhZ2UgPSBGQUxTRSwKICAgICAgICAgICAgICAgICAgICAgIGZpZy5oZWlnaHQgPSA1LCBmaWcud2lkdGggPSA2LCBmaWcuYWxpZ24gPSAiY2VudGVyIikKCnNldC5zZWVkKDEyMzQ1KQpsaWJyYXJ5KGRwbHlyKQpsaWJyYXJ5KHRpZHlyKQpsaWJyYXJ5KGdncGxvdDIpCmxpYnJhcnkobGF0dGljZSkKbGlicmFyeShncmlkRXh0cmEpCmxpYnJhcnkocGF0Y2h3b3JrKQpzb3VyY2UoaGVyZTo6aGVyZSgiZGF0YXNldHMuUiIpKQp0aGVtZV9zZXQodGhlbWVfbWluaW1hbCgpICsKICAgICAgICAgIHRoZW1lKHRleHQgPSBlbGVtZW50X3RleHQoc2l6ZSA9IDE2KSwKICAgICAgICAgICAgICAgIHBhbmVsLmJvcmRlciA9IGVsZW1lbnRfcmVjdChjb2xvciA9ICJncmV5MzAiLCBmaWxsID0gTkEpKSkKYGBgCgojIyBTY2FsYWJpbGl0eQoKU2NhdHRlciBwbG90cyB3b3JrIHdlbGwgZm9yIGh1bmRyZWRzIG9mIG9ic2VydmF0aW9ucwoKT3Zlci1wbG90dGluZyBiZWNvbWVzIGFuIGlzc3VlIG9uY2UgdGhlIG51bWJlciBvZiBvYnNlcnZhdGlvbnMgZ2V0cwppbnRvIHRlbnMgb2YgdGhvdXNhbmRzLgoKRm9yIHNvbWUgb3V0cHV0IGZvcm1hdHMgc3RvcmFnZSBhbHNvIGJlY29tZXMgYW4gaXNzdWUgYXMgdGhlIG51bWJlciBvZgpwb2ludHMgcGxvdHRlZCBpbmNyZWFzZXMuCgpTb21lIHNpbXVsYXRlZCBkYXRhOgoKYGBge3Igc2ltdWxhdGVkLWRhdGEtcGxvdHMsIGV2YWwgPSBGQUxTRSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9Cm4gPC0gNTAwMDAKIyMgbjUwSyA8LSBkYXRhLmZyYW1lKHggPSBybm9ybShuKSwgeSA9IHJub3JtKG4pKQp4IDwtIHJub3JtKG4pCnkgPC0geCArIDAuNCAqIHggXiAyICsgcm5vcm0obikKeSA8LSB5IC8gc2QoeSkKbjUwSyA8LSBkYXRhLmZyYW1lKHggPSB4LCB5ID0geSkKCm4xMEsgPC0gbjUwS1sxIDogMTAwMDAsIF0KbjFLIDwtIG41MEtbMSA6IDEwMDAsIF0KcDEgPC0gZ2dwbG90KG4xSywgYWVzKHgsIHkpKSArCiAgICBnZW9tX3BvaW50KCkgKwogICAgY29vcmRfZXF1YWwoKSArCiAgICBnZ3RpdGxlKHNwcmludGYoIiVkIFBvaW50cyIsIG5yb3cobjFLKSkpCnAyIDwtIGdncGxvdChuMTBLLCBhZXMoeCwgeSkpICsKICAgIGdlb21fcG9pbnQoKSArCiAgICBjb29yZF9lcXVhbCgpICsKICAgIGdndGl0bGUoc3ByaW50ZigiJWQgUG9pbnRzIiwgbnJvdyhuMTBLKSkpCmxpYnJhcnkocGF0Y2h3b3JrKQpwMSB8IHAyCmBgYAoKYGBge3Igc2ltdWxhdGVkLWRhdGEtcGxvdHMsIGZpZy53aWR0aCA9IDgsIGVjaG8gPSBGQUxTRX0KYGBgCgoKIyMgU29tZSBTaW1wbGUgT3B0aW9ucwoKU2ltcGxlIG9wdGlvbnMgdG8gYWRkcmVzcyBvdmVyLXBsb3R0aW5nOgoKKiBzYW1wbGluZwoKKiByZWR1Y2luZyB0aGUgcG9pbnQgc2l6ZQoKKiBhbHBoYSBibGVuZGluZwoKV2l0aCBubyBhZGp1c3RtZW50czoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcDIgKyB4bGltKGMoLTUsIDUpKSArIHlsaW0oYygtMywgMTApKQpgYGAKClJlZHVjaW5nIHRoZSBwb2ludCBzaXplIGhlbHBzIHdoZW4gdGhlIG51bWJlciBvZiBwb2ludHMgaXMgaW4gdGhlIGxvdwp0ZW5zIG9mIHRob3VzYW5kczoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KG4xMEssIGFlcyh4LCB5KSkgKwogICAgZ2VvbV9wb2ludChzaXplID0gMC4xKSArCiAgICBjb29yZF9lcXVhbCgpICsKICAgIHhsaW0oYygtNSwgNSkpICsKICAgIHlsaW0oYygtMywgMTApKSArCiAgICBnZ3RpdGxlKHNwcmludGYoIiVkIFBvaW50cyIsIG5yb3cobjEwSykpKQpgYGAKCkFscGhhIGJsZW5kaW5nIGNhbiBhbHNvIGJlIGVmZmVjdGl2ZSwgb24gaXRzIG93biBvciBpbiBjb21iaW5hdGlvbgp3aXRoIHBvaW50IHNpemUgYWRqdXN0bWVudDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KG41MEssIGFlcyh4LCB5KSkgKwogICAgZ2VvbV9wb2ludChhbHBoYSA9IDAuMDEsIHNpemUgPSAwLjUpICsKICAgIGNvb3JkX2VxdWFsKCkgKwogICAgeGxpbShjKC01LCA1KSkgKwogICAgeWxpbShjKC0zLCAxMCkpICsKICAgIGdndGl0bGUoc3ByaW50ZigiJWQgUG9pbnRzIiwgbnJvdyhuNTBLKSkpCmBgYAoKRXhwZXJpbWVudGF0aW9uIGlzIHVzdWFsbHkgbmVlZGVkIHRvIGlkZW50aWZ5IGEgZ29vZCBwb2ludCBzaXplIGFuZAphbHBoYSBsZXZlbC4KCkJvdGggYWxwaGEgYmxlbmRpbmcgYW5kIHBvaW50IHNpemUgcmVkdWN0aW9uIGluaGliaXQgdGhlIHVzZSBvZiBjb2xvcgpmb3IgZW5jb2RpbmcgYSBncm91cGluZyB2YXJpYWJsZS4KClRoZSBiZXN0IGNob2ljZXMgbWF5IHZhcnkgZnJvbSBvbmUgb3V0cHV0IGZvcm1hdCB0byBhbm90aGVyLgoKCiMjIERlbnNpdHkgRXN0aW1hdGlvbiBNZXRob2RzCgpTb21lIG1ldGhvZHMgYmFzZWQgb24gZGVuc2l0eSBlc3RpbWF0aW9uIG9yIGJpbm5pbmc6CgoqIERpc3BsYXlpbmcgY29udG91cnMgb2YgYSAyRCBkZW5zaXR5IGVzdGltYXRlLgoKKiBFbmNvZGluZyBkZW5zaXR5IGVzdGltYXRlcyBpbiBwb2ludCBzaXplLgoKKiBIZXhhZ29uYWwgYmlubmluZy4KCgojIyMgRGVuc2l0eSBDb250b3VycwoKQSAyRCBkZW5zaXR5IGVzdGltYXRlIGNhbiBiZSBkaXNwbGF5ZWQgaW4gdGVybXMgb2YgaXRzIF9jb250b3Vyc18sIG9yCl9sZXZlbCBjdXJ2ZXNfLgoKYGBge3IsIGZpZy5oZWlnaHQgPSA0Ljc1LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcCA8LSBnZ3Bsb3QobjUwSywgYWVzKHgsIHkpKSArCiAgICBjb29yZF9lcXVhbCgpICsKICAgIGdndGl0bGUoc3ByaW50ZigiJWQgUG9pbnRzIiwgbnJvdyhuNTBLKSkpCnBwIDwtIGdlb21fcG9pbnQoYWxwaGEgPSAwLjAxLCBzaXplID0gMC41KQpkZCA8LSBnZW9tX2RlbnNpdHlfMmQoY29sb3IgPSAicmVkIikKcCArIGRkCmBgYAoKVGhlc2UgYXJlIHRoZSBjb250b3VycyBvZiB0aGUgZXN0aW1hdGVkIGRlbnNpdHkgc3VyZmFjZToKCmBgYHtyLCBmaWcuaGVpZ2h0ID0gNC43NSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmQgPC0gTUFTUzo6a2RlMmQobjUwSyR4LCBuNTBLJHksIG4gPSA1MCkKdiA8LSBleHBhbmQuZ3JpZCh4ID0gZCR4LCB5ID0gZCR5KQp2JHogPC0gYXMubnVtZXJpYyhkJHopCmxhdHRpY2U6OndpcmVmcmFtZSh6IH4geCArIHksCiAgICAgICAgICAgICAgICAgICBkYXRhID0gdiwKICAgICAgICAgICAgICAgICAgIHNjcmVlbiA9IGxpc3QoeiA9IDcwLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICB4ID0gLTYwKSkKYGBgCgoyRCBkZW5zaXR5IGVzdGltYXRlIGNvbnRvdXJzIGNhbiBiZSBzdXBlcmltcG9zZWQgb24gYSBzZXQgb2YgcG9pbnRzIG9yCnBsYWNlZCBiZW5lYXRoIGEgc2V0IG9mIHBvaW50czoKCmBgYHtyLCBmaWcud2lkdGggPSA4LCBmaWcuaGVpZ2h0ID0gNiwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAxIDwtIHAgKyBsaXN0KHBwLCBkZCkKcDIgPC0gcCArIGxpc3QoZGQsIHBwKQpwMSB8IHAyCmBgYAoKCiMjIyBEZW5zaXR5IExldmVscyBFbmNvZGVkIHdpdGggUG9pbnQgU2l6ZQoKRGVuc2l0eSBsZXZlbHMgY2FuIGFsc28gYmUgZW5jb2RlZCBpbiBwb2ludCBzaXplIGluIGEgZ3JpZCBvZiBwb2ludHM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgKyBzdGF0X2RlbnNpdHlfMmQoCiAgICAgICAgYWVzKHNpemUgPSBhZnRlcl9zdGF0KGRlbnNpdHkpKSwKICAgICAgICBnZW9tID0gInBvaW50IiwKICAgICAgICBuID0gMzAsCiAgICAgICAgY29udG91ciA9IEZBTFNFKSArCiAgICBzY2FsZV9zaXplKHJhbmdlID0gYygwLCA2KSkKYGBgCgpUaGlzIHNjYWxlcyB3ZWxsIGNvbXB1dGF0aW9uYWxseQoKSXQgZG9lcyBub3QgZWFzaWx5IHN1cHBvcnQgZW5jb2RpbmcgYSBncm91cGluZyB3aXRoIGNvbG9yIG9yIHNoYXBlLgoKSXQgaW50cm9kdWNlcyBzb21lIGRpc3RyYWN0aW5nIHZpc3VhbCBhcnRpZmFjdHMgdGhhdCBhcmUgcmVsYXRlZCB0bwpzb21lIG9wdGljYWwgaWxsdXNpb25zIFtzZWVuCmVhcmxpZXJdKHBlcmNlcC5odG1sI3NvbWUtb3B0aWNhbC1pbGx1c2lvbnMpLgoKVGhpcyBlZmZlY3QgY2FuIGJlIHJlZHVjZWQgc29tZXdoYXQgYnkgaml0dGVyaW5nOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifSAgICAgCmppdF9hbXQgPC0gMC4wMwpwICsgc3RhdF9kZW5zaXR5XzJkKAogICAgICAgIGFlcyhzaXplID0gYWZ0ZXJfc3RhdChkZW5zaXR5KSksCiAgICAgICAgZ2VvbSA9ICJwb2ludCIsCiAgICAgICAgcG9zaXRpb24gPSBwb3NpdGlvbl9qaXR0ZXIoaml0X2FtdCwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBqaXRfYW10KSwKICAgICAgICBuID0gMzAsIGNvbnRvdXIgPSBGQUxTRSkgKwogICAgc2NhbGVfc2l6ZShyYW5nZSA9IGMoMCwgNikpCmBgYAoKCiMjIyBIZXhhZ29uYWwgQmlubmluZwoKSGV4YWdvbmFsIGJpbm5pbmcgZGl2aWRlcyB0aGUgcGxhbmUgaW50byBoZXhhZ29uYWwgYmlucyBhbmQgZGlzcGxheXMKdGhlIG51bWJlciBvZiBwb2ludHMgaW4gZWFjaCBiaW46CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgKyBnZW9tX2hleCgpCmBgYAoKVGhpcyBhbHNvIHNjYWxlcyB2ZXJ5IHdlbGwgdG8gbGFyZ2VyIGRhdGEgc2V0cy4KClRoZSBkZWZhdWx0IGNvbG9yIHNjaGVtZSBzZWVtcyBsZXNzIHRoYW4gaWRlYWwuCgpBbiBhbHRlcm5hdGl2ZSBmaWxsIGNvbG9yIGNob2ljZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcCArIGdlb21faGV4KCkgKwogICAgc2NhbGVfZmlsbF9ncmFkaWVudChsb3cgPSAiZ3JheSIsCiAgICAgICAgICAgICAgICAgICAgICAgIGhpZ2ggPSAiYmxhY2siKQpgYGAKCkFnYWluIGl0IGlzIHBvc3NpYmxlIHRvIHVzZSBhIHNjYWxlZCBwb2ludCByZXByZXNlbnRhdGlvbjoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcCArIHN0YXRfYmluX2hleCgKICAgICAgICBnZW9tID0gInBvaW50IiwKICAgICAgICBhZXMoc2l6ZSA9IGFmdGVyX3N0YXQoZGVuc2l0eSkpLAogICAgICAgIGZpbGwgPSBOQSkKYGBgCgpUaGlzIHJlcHJlc2VudGF0aW9uIHN0aWxsIHByb2R1Y2VzIHNvbWUgdmlzdWFsIGRpc3RyYWN0aW9ucywgYnV0IGxlc3MKdGhhbiBhIHJlY3Rhbmd1bGFyIGdyaWQuCgpBZ2Fpbiwgaml0dGVyaW5nIGNhbiBoZWxwOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpqaXRfYW10IDwtIDAuMDUKcCArIHN0YXRfYmluX2hleCgKICAgICAgICBhZXMoc2l6ZSA9IGFmdGVyX3N0YXQoZGVuc2l0eSkpLAogICAgICAgIGdlb20gPSAicG9pbnQiLAogICAgICAgIHBvc2l0aW9uID0gcG9zaXRpb25faml0dGVyKGppdF9hbXQsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgaml0X2FtdCksCiAgICAgICAgZmlsbCA9IE5BKQpgYGAKCgojIyMgT3RoZXIgRGVuc2l0eSBQbG90cwoKVGhlIGBoZHJjZGVgIHBhY2thZ2UgY29tcHV0ZXMgYW5kIHBsb3RzIGRlbnNpdHkgY29udG91cnMgY29udGFpbmluZwpzcGVjaWZpZWQgcHJvcG9ydGlvbnMgb2YgdGhlIGRhdGEuCgpUaGUgYGhkci5ib3hwbG90LjJkYCBmdW5jdGlvbiBwbG90cyB0aGVzZSBjb250b3VycyBhbmQgc2hvd3MgdGhlCnBvaW50cyBub3QgaW4gdGhlIG91dGVybW9zdCBjb250b3VyOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpsaWJyYXJ5KGhkcmNkZSkKd2l0aChuNTBLLAogICAgIGhkci5ib3hwbG90LjJkKHgsIHksCiAgICAgICAgICAgICAgICAgICAgcHJvYiA9IGMoMC4xLCAwLjUsIDAuNzUsIDAuOSkpKQpgYGAKPCEtLQpJdCBzaG91bGQgYmUgcG9zc2libGUgdG8gc2VsZWN0IHRoZSBjb250b3VyIGxldmVscyB1c2VkIGluIGBnZ3Bsb3RgIGluIGEKc2ltaWxhciB3YXkuCi0tPgoKCiMjIFNvbWUgRW5oYW5jZW1lbnRzCgoKIyMjIEVuY29kaW5nIEFkZGl0aW9uYWwgVmFyaWFibGVzCgpTY2F0dGVyIHBsb3RzIGNhbiBlbmNvZGUgaW5mb3JtYXRpb24gYWJvdXQgb3RoZXIgdmFyaWFibGVzIHVzaW5nCgoqIHN5bWJvbCBjb2xvcgoKKiBzeW1ib2wgc2l6ZQoKKiBzeW1ib2wgc2hhcGUKCkFuIGV4YW1wbGUgdXNpbmcgdGhlIGBtcGdgIGRhdGEgc2V0OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwIDwtIGdncGxvdChtcGcsIGFlcyhjdHksIGh3eSwKICAgICAgICAgICAgICAgICAgICAgY29sb3IgPSBmYWN0b3IoY3lsKSkpCnAgKyBnZW9tX3BvaW50KGFlcyhzaXplID0gZHJ2KSkKYGBgCgpTb21lIGVuY29kaW5ncyB3b3JrIGJldHRlciB0aGFuIG90aGVyczoKCiogU2l6ZSBpcyBub3QgYSBnb29kIGZpdCBmb3IgYSBkaXNjcmV0ZSB2YXJpYWJsZQoKKiBFdmVuIHRob3VnaCBgY3lsYCBpcyBudW1lcmljLCBpdCBpcyBiZXN0IGVuY29kZWQgYXMgY2F0ZWdvcmljYWwuCgoqIFNpemUgYW5kIGNvbG9yIGludGVyZmVyZSB3aXRoIGVhY2ggb3RoZXIgYXMgdGhlIGNvbG9yIG9mIHNtYWxsZXIKICBvYmplY3RzIGlzIGhhcmRlciB0byBwZXJjZWl2ZS4KCiogU2ltaWxhcmx5LCBzaXplIGFuZCBzaGFwZSBpbnRlcmZlcmUgd2l0aCBlYWNoIG90aGVyLgoKVXNpbmcgYHNoYXBlYCBpbnN0ZWFkIG9mIGBzaXplYCBmb3IgYGRydmA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgKyBnZW9tX3BvaW50KGFlcyhzaGFwZSA9IGRydikpCmBgYAoKSW5jcmVhc2luZyB0aGUgc2l6ZSBtYWtlcyBzaGFwZXMgYW5kIHRoZSBjb2xvcnMgZWFzaWVyIHRvIGRpc3Rpbmd1aXNoOgoKYGBge3J9CnAgKyBnZW9tX3BvaW50KGFlcyhzaGFwZSA9IGRydiksIHNpemUgPSAzKQpgYGAKCgojIyMgTWFyZ2luYWwgUGxvdHMKClRoZSBgZ2dNYXJnaW5gIGZ1bmN0aW9uIGluIHRoZSBgZ2dFeHRyYWAgcGFja2FnZSBhdHRhY2hlcyBtYXJnaW5hbApoaXN0b2dyYW1zIHRvIChzb21lKSBwbG90cyBwcm9kdWNlZCBieSBgZ2dwbG90YDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShnZ0V4dHJhKQpwIDwtIGdncGxvdChuNTBLLCBhZXMoeCwgeSkpICsKICAgIGdlb21fcG9pbnQoYWxwaGEgPSAwLjAxLCBzaXplID0gMC41KQpnZ01hcmdpbmFsKHAsCiAgICAgICAgICAgdHlwZSA9ICJoaXN0b2dyYW0iLAogICAgICAgICAgIGJpbnMgPSA1MCwKICAgICAgICAgICBmaWxsID0gImxpZ2h0Z3JleSIpCmBgYAoKVGhlIGRlZmF1bHQgdHlwZSBpcyBgImRlbnNpdHkiYCBmb3IgYSBtYXJnaW5hbCBkZW5zaXR5IHBsb3Q6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdnTWFyZ2luYWwocCwgZmlsbCA9ICJsaWdodGdyZXkiKQpgYGAKCkZvciBkYXRhIHNldHMgb2YgbW9yZSBtb2Rlc3Qgc2l6ZSBydWcgcGxvdHMgYWxvbmcgdGhlIGF4ZXMgY2FuIGJlCnVzZWZ1bDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGZhaXRoZnVsLAogICAgICAgYWVzKGVydXB0aW9ucywgd2FpdGluZykpICsKICAgIGdlb21fcG9pbnQoKSArCiAgICBnZW9tX3J1ZyhhbHBoYSA9IDAuMikKYGBgCgoKIyMjIEFkZGluZyBhIFNtb290aCBDdXJ2ZQoKV2hlbiB0aGUgdmFyaWFibGVzIG9uIHRoZSAkeSQgYXhpcyBpcyBhIHJlc3BvbnNlIHZhcmlhYmxlIGEgdXNlZnVsCmVuaGFuY2VtZW50IGlzIHRvIGFkZCBhIHNtb290aCBjdXJ2ZSB0byBhIHBsb3QuCgpUaGUgZGVmYXVsdCBtZXRob2QgaXMgYSBmb3JtIG9mIGxvY2FsIGF2ZXJhZ2luZywgYW5kIGluY2x1ZGVzIGEKcmVwcmVzZW50YXRpb24gb2YgdW5jZXJ0YWludHk6CgpgYGB7ciwgZmlnLndpZHRoID0gOSwgZmlnLmhlaWdodCA9IDQuMjUsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwMSA8LSBnZ3Bsb3QoZmFpdGhmdWwsIGFlcyhlcnVwdGlvbnMsIHdhaXRpbmcpKSArCiAgICBnZW9tX3BvaW50KCkgKwogICAgZ2VvbV9zbW9vdGgoKSArCiAgICBnZ3RpdGxlKCJPbGQgRmFpdGhmdWwgRXJ1cHRpb25zIikKcDIgPC0gZ2dwbG90KG41MEssIGFlcyh4LCB5KSkgKwogICAgcHAgKwogICAgZ2VvbV9zbW9vdGgoKSArCiAgICBnZ3RpdGxlKHNwcmludGYoIiVkIFBvaW50cyIsIG5yb3cobjUwSykpKQpwMSB8IHAyCmBgYAoKCiMjIyBBeGlzIFRyYW5zZm9ybWF0aW9uCgpWYXJpYWJsZSB0cmFuc2Zvcm1hdGlvbnMgYXJlIG9mdGVuIGhlbHBmdWwuCgpWYXJpYWJsZSB0cmFuc2Zvcm1hdGlvbnMgY2FuIGJlIGFwcGxpZWQgYnkKCiogcGxvdHRpbmcgdGhlIHRyYW5zZm9ybWVkIGRhdGEKCiogcGxvdHRpbmcgb24gdHJhbnNmb3JtZWQgYXhlcwoKQXhpcyB0cmFuc2Zvcm1hdGlvbnMgYGdncGxvdGAgc3VwcG9ydHM6CgoqIGBsb2cxMGAgd2l0aCBgc2NhbGVfeF9sb2cxMGAsIHNjYWxlX3lfbG9nMTAKCiogc3F1YXJlIHJvb3Qgd2l0aCBgc2NhbGVfeF9zcXJ0YCwgYHNjYWxlX3lfc3FydGAKCiogcmV2ZXJzZWQgYXhlcyB3aXRoIGBzY2FsZV94X3JldmVyc2VgLCBgc2NhbGVfeV9yZXZlcnNlYAoKQ2hhbmdpbmcgc2NhbGVzIGNhbiBtYWtlIHBsb3Qgc2hhcGVzIHNpbXBsZXIsIGJ1dCBub24tbGluZWFyIGF4ZXMgYXJlCmhhcmRlciB0byBpbnRlcnByZXQuCgpgYGB7ciwgZmlnLndpZHRoID0gOSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmxpYnJhcnkoZ2FwbWluZGVyKQpnYXAgPC0gZmlsdGVyKGdhcG1pbmRlciwgeWVhciA9PSAyMDA3KQpwIDwtIGdncGxvdChnYXAsCiAgICAgICAgICAgIGFlcyh4ID0gZ2RwUGVyY2FwLAogICAgICAgICAgICAgICAgeSA9IGxpZmVFeHAsCiAgICAgICAgICAgICAgICBjb2xvciA9IGNvbnRpbmVudCwKICAgICAgICAgICAgICAgIHNpemUgPSBwb3ApKSArCiAgICBnZW9tX3BvaW50KCkgKwogICAgc2NhbGVfc2l6ZV9hcmVhKG1heF9zaXplID0gOCkKcDEgPC0gcCArCiAgICBndWlkZXMoY29sb3IgPSAibm9uZSIsCiAgICAgICAgICAgc2l6ZSA9ICJub25lIikKcDIgPC0gcCArCiAgICBzY2FsZV94X2xvZzEwKCkgKwogICAgZ3VpZGVzKHNpemUgPSAibm9uZSIpCnAxICsgcDIKYGBgCgoKIyMgQ29uZGl0aW9uaW5nCgpXaGVuIHRoZSAkeSQgdmFyaWFibGUgaXMgYSByZXNwb25zZSBpdCBjYW4gYWxzbyBiZSB1c2VmdWwgdG8gZXhwbG9yZQp0aGUgY29uZGl0aW9uYWwgZGlzdHJpYnV0aW9uIG9mICR5JCBnaXZlbiBkaWZmZXJlbnQgdmFsdWVzIG9mIHRoZSAkeCQKdmFyaWFibGUuCgpPbmUgd2F5IHRvIGRvIHRoaXMgaXMgdG8gZm9jdXMgb24gdGhlIGRhdGEgZm9yIG5hcnJvdyByYW5nZXMgb2YgdGhlCmNvbmRpdGlvbmluZyB2YXJpYWJsZS4KClR3byBhcHByb2FjaGVzIGZvciBjcmVhdGluZyBncm91cHMgdG8gZm9jdXMgb246CgoqIFVzZSB0aGUgYGJhc2VgIGZ1bmN0aW9uIGBjdXRgLCBvciBvbmUgb2YgdGhlIGBnZ2xvdDJgIGZ1bmN0aW9ucwoKICAgICogYGN1dF9pbnRlcnZhbGAKICAgICogYGN1dF9udW1iZXJgCiAgICAqIGBjdXRfd2lkdGhgCgoqIFVzZSB0aGUgYHJvdW5kYCBmdW5jdGlvbi4KClJvdW5kaW5nIHRvIGFuIGludGVnZXIgb3IgdXNpbmcKCmBgYHtyLCBldmFsID0gRkFMU0V9CmN1dF93aWR0aCh4LCB3aWR0aCA9IDEsIGNlbnRlciA9IDApCmBgYAoKcHJvZHVjZXMgdGhlc2UgYmluczoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcCA8LSBnZ3Bsb3QobjUwSywgYWVzKHgsIHkpKSArCiAgICBnZW9tX3BvaW50KGFscGhhID0gMC4wNSwgc2l6ZSA9IDAuNSkKcCArIGdlb21fdmxpbmUoeGludGVyY2VwdCA9CiAgICAgICAgICAgICAgICAgICBzZXEoLTMuNSwgNC41LCBieSA9IDEpLAogICAgICAgICAgICAgICBsaW5ldHlwZSA9IDIsCiAgICAgICAgICAgICAgIGNvbG9yID0gInJlZCIpICsKICAgIHNjYWxlX3hfY29udGludW91cyhicmVha3MgPSBzZXEoLTMsIDQpLAogICAgICAgICAgICAgICAgICAgICAgIGxhYmVscyA9IGFzLmNoYXJhY3RlcihzZXEoLTMsIDQpKSkKYGBgCgpEYXRhIHdpdGhpbiBlYWNoIGdyb3VwIGNhbiB0aGVuIGJlIHNob3duIHVzaW5nIGJveCBwbG90cyAoeW91IG5lZWQgdG8KdXNlIHRoZSBgZ3JvdXBgIGFlc3RoZXRpYyB0byBwbG90IG9uIGEgY29udGludW91cyBheGlzKToKCmBgYHtyfQpuNTBLX3RybSA8LSBmaWx0ZXIobjUwSywgeCA+IC0yLjUsIHggPCAyLjUpCm11dGF0ZShuNTBLX3RybSwgeHJuZCA9IHJvdW5kKHgpKSB8PgogICAgZ2dwbG90KGFlcyh4LCB5KSkgKwogICAgZ2VvbV9ib3hwbG90KGFlcyhncm91cCA9IHhybmQpKQpgYGAKClVzaW5nIGBjdXRfd2lkdGhgIGFuZCB2aW9saW4gcGxvdHM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9Cm11dGF0ZShuNTBLX3RybSwKICAgICAgIHhjdXQgPSBjdXRfd2lkdGgoeCwKICAgICAgICAgICAgICAgICAgICAgICAgd2lkdGggPSAxLAogICAgICAgICAgICAgICAgICAgICAgICBjZW50ZXIgPSAwKSkgfD4KICAgIGdyb3VwX2J5KHhjdXQpIHw+CiAgICBtdXRhdGUoeG1lZCA9IG1lZGlhbih4KSkgfD4KICAgIHVuZ3JvdXAoKSB8PgogICAgZ2dwbG90KGFlcyh4LCB5KSkgKwogICAgZ2VvbV92aW9saW4oYWVzKGdyb3VwID0geG1lZCksCiAgICAgICAgICAgICAgICBkcmF3X3F1YW50aWxlcyA9IDAuNSkKYGBgCgpBbm90aGVyIG9wdGlvbiBmb3IgdmlzdWFsaXppbmcgdGhlIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMgaXMKZmFjZXRlZCBkZW5zaXR5IHBsb3RzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQptdXRhdGUobjUwS190cm0sIHhybmQgPSByb3VuZCh4KSkgfD4KICAgIGdncGxvdChhZXMoeCkpICsKICAgIGdlb21fZGVuc2l0eShhZXMoeSkpICsKICAgIGZhY2V0X3dyYXAofiB4cm5kLCBuY29sID0gMSkKYGBgCgpEZW5zaXR5IHJpZGdlcyB3b3JrIGFzIHdlbGw6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CiN8IHdhcm5pbmc6IGZhbHNlCmxpYnJhcnkoZ2dyaWRnZXMpCm11dGF0ZShuNTBLX3RybSwgeHJuZCA9IHJvdW5kKHgpKSB8PgogICAgZ2dwbG90KGFlcyh5LCB4cm5kLCBncm91cCA9IHhybmQpKSArCiAgICBnZW9tX2RlbnNpdHlfcmlkZ2VzKHF1YW50aWxlX2xpbmVzID0gVFJVRSwKICAgICAgICAgICAgICAgICAgICAgICAgcXVhbnRpbGVzID0gMikKYGBgCgpVc2luZyBhIGxhcmdlciBzZXQgb2YgbmFycm93ZXIgYmlucyBjZW50ZXJlZCBvbiBtdWx0aXBsZXMgb2YgMS8yOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQptdXRhdGUobjUwS190cm0sIHhybmQgPSByb3VuZCgyICogeCkgLyAyKSB8PgogICAgZ2dwbG90KGFlcyh5LCB4cm5kLCBncm91cCA9IHhybmQpKSArCiAgICBnZW9tX2RlbnNpdHlfcmlkZ2VzKHF1YW50aWxlX2xpbmVzID0gVFJVRSwKICAgICAgICAgICAgICAgICAgICAgICAgcXVhbnRpbGVzID0gMikKYGBgCgpTb21ldGltZXMgaXQgaXMgdXNlZnVsIHRvIHVzZSBhIHNtYWxsIG51bWJlciBvZiBuYXJyb3cgYmluczoKCmBgYHtyLCBmaWcud2lkdGggPSA5LCBmaWcuaGVpZ2h0ID0gNCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnJkYXRhIDwtIGRhdGEuZnJhbWUoeG1pbiA9ICgtMiA6IDIpIC0gMC4xLAogICAgICAgICAgICAgICAgICAgIHhtYXggPSAoLTIgOiAyKSArIDAuMSwKICAgICAgICAgICAgICAgICAgICB5bWluID0gLUluZiwKICAgICAgICAgICAgICAgICAgICB5bWF4ID0gSW5mKQpwMSA8LSBwICsgZ2VvbV9yZWN0KGFlcyh4bWluID0geG1pbiwgeG1heCA9IHhtYXgsIHltaW4gPSB5bWluLCB5bWF4ID0geW1heCksCiAgICAgICAgICAgICAgICAgICAgZGF0YSA9IHJkYXRhLAogICAgICAgICAgICAgICAgICAgIGluaGVyaXQuYWVzID0gRkFMU0UsCiAgICAgICAgICAgICAgICAgICAgZmlsbCA9ICJyZWQiLAogICAgICAgICAgICAgICAgICAgIGFscGhhID0gMC4yKQoKcDIgPC0gbXV0YXRlKG41MEtfdHJtLCB4cm5kID0gcm91bmQoeCkpIHw+CiAgICBmaWx0ZXIoYWJzKHggLSB4cm5kKSA8IDAuMSkgfD4KICAgIGdncGxvdChhZXMoeSwgeHJuZCwgZ3JvdXAgPSB4cm5kKSkgKwogICAgZ2VvbV9kZW5zaXR5X3JpZGdlcyhxdWFudGlsZV9saW5lcyA9IFRSVUUsIHF1YW50aWxlcyA9IDIpCnAxIHwgcDIKYGBgCgpGb3IgZXhhbWluaW5nIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMsIGJpbnMgbmVlZCB0byBiZToKCiogbmFycm93IGVub3VnaCB0byBmb2N1cyBvbiBhIHBhcnRpY3VsYXIgJHgkIHZhbHVlOwoKKiB3aWRlIGVub3VnaCB0byBpbmNsdWRlIGVub3VnaCBvYnNlcnZhdGlvbnMgZm9yIGEgdXNlZnVsIHZpc3VhbGl6YXRpb24uCgpGb3Igc21hbGxlciBkYXRhIHNldHMgaXQgY2FuIGFsc28gYmUgdXNlZnVsIHRvIGFsbG93IGJpbnMgdG8gb3ZlcmxhcC4KCiogYGdncGxvdGAgZG9lcyBub3QgcHJvdmlkZSBzdXBwb3J0IGZvciB0aGlzLgoKKiBgbGF0dGljZWAgZG9lcyBzdXBwb3J0IHRoaXMgd2l0aCBfc2hpbmdsZXNfLgoKVGhlIGxhdHRpY2UgZnVuY3Rpb25zIGBzaGluZ2xlYCBhbmQgYGVxdWFsLmNvdW50YCBjcmVhdGUgc2hpbmdsZXMgdGhhdApjYW4gYmUgdXNlZCBpbiBgbGF0dGljZWAtc3R5bGUgZmFjZXRpbmcuCgoKIyMgRXhhbXBsZTogRGlhbW9uZCBQcmljZXMKClRoZSBgZGlhbW9uZHNgIGRhdGEgc2V0IGNvbnRhaW5zIHByaWNlcyBhbmQgb3RoZXIgYXR0cmlidXRlcyBmb3IKYHIgc2NhbGVzOjpjb21tYShucm93KGRpYW1vbmRzKSlgIGRpYW1vbmRzLgoKVGhlIGBjdXRgIHZhcmlhYmxlIGluZGljYXRlcyB0aGUgX3F1YWxpdHlfIG9mIGEgZGlhbW9uZCdzIGN1dC4KCllvdSBtaWdodCBleHBlY3QgJ2JldHRlcicgY3V0cyB0byBjb3N0IG1vcmUsIGJ1dCB0aGF0IGlzIG5vdCB0cnVlIG9uCmF2ZXJhZ2U6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9Cm1tIDwtIGdyb3VwX2J5KGRpYW1vbmRzLCBjdXQpIHw+CiAgICBzdW1tYXJpemUobWVkX3ByaWNlID0gbWVkaWFuKHByaWNlKSwKICAgICAgICAgICAgICBhdmdfcHJpY2UgPSBtZWFuKHByaWNlKSwKICAgICAgICAgICAgICBuID0gbGVuZ3RoKHByaWNlKSkgfD4KICAgIHBpdm90X2xvbmdlcigyIDogMywKICAgICAgICAgICAgICAgICBuYW1lc190byA9ICJ3aGljaCIsCiAgICAgICAgICAgICAgICAgdmFsdWVzX3RvID0gInByaWNlIikKZ2dwbG90KG1tLCBhZXMoeCA9IHByaWNlLAogICAgICAgICAgICAgICB5ID0gY3V0LAogICAgICAgICAgICAgICBjb2xvciA9IHdoaWNoKSkgKwogICAgZ2VvbV9wb2ludCgsIHNpemUgPSAzKQpgYGAKClRoZSBwcm9wb3J0aW9uIG9mIGRpYW1vbmRzIGF0IGVhY2ggYGN1dGAgbGV2ZWwgaXMgYWxzbyBwZXJoYXBzIHN1cnByaXNpbmc6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcykgKwogICAgZ2VvbV9iYXIoYWVzKHggPSBjdXQpLAogICAgICAgICAgICAgZmlsbCA9ICJkZWVwc2t5Ymx1ZTMiKQpgYGAKCkFuZCB0aGUgcHJpY2UgZGlzdHJpYnV0aW9ucyB3aXRoaW4gZWFjaCBgY3V0YCBsZXZlbCBkaWZmZXIgaW4gc2hhcGU6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcywgYWVzKHggPSBwcmljZSwgeSA9IGN1dCkpICsKICAgIGdlb21fdmlvbGluKCkgKwogICAgZ2VvbV9wb2ludChhZXMoY29sb3IgPSB3aGljaCksIGRhdGEgPSBtbSkKYGBgCgpBbm90aGVyIGltcG9ydGFudCBmYWN0b3IgaXMgdGhlIHNpemUsIG1lYXN1cmVkIGluIGBjYXJhdGAuCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcywgYWVzKHggPSBjYXJhdCwgeSA9IGN1dCkpICsKICAgIGdlb21fdmlvbGluKCkKYGBgCgpIaXN0b2dyYW1zIHdpdGggYSBuYXJyb3cgYmluIHdpZHRoIG1heSBoZWxwIHVuZGVyc3RhbmQgdGhlIHVudXN1YWwgc2hhcGVzLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21faGlzdG9ncmFtKGFlcyhjYXJhdCksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDAuMDEpCmBgYAoKVHJ5IGZhY2V0aW5nIG9uIGBjdXRgOgoKYGBge3IsIGZpZy5oZWlnaHQgPSA2LjUsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21faGlzdG9ncmFtKGFlcyhjYXJhdCksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDAuMDEpICsKICAgIGZhY2V0X3dyYXAofiBjdXQsIG5jb2wgPSAxKQpgYGAKClRvIGZvY3VzIG9uIHRoZSBzaGFwZXMgb2YgdGhlIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMgb2YgY2FyYXQgZ2l2ZW4KY3V0IHVzZSBgeSA9IGFmdGVyX3N0YXQoZGVuc2l0eSlgOgoKYGBge3IsIGZpZy5oZWlnaHQgPSA2LjUsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21faGlzdG9ncmFtKAogICAgICAgIGFlcyh4ID0gY2FyYXQsCiAgICAgICAgICAgIHkgPSBhZnRlcl9zdGF0KGRlbnNpdHkpKSwKICAgICAgICBiaW53aWR0aCA9IDAuMDEpICsKICAgIGZhY2V0X3dyYXAofiBjdXQsIG5jb2wgPSAxKQpgYGAKCkFsdGVybmF0aXZlbHksIHlvdSBjYW4gZmFjZXQgd2l0aCBgc2NhbGVzID0gImZyZWVfeSJgOgoKYGBge3IsIGZpZy5oZWlnaHQgPSA2LjUsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21faGlzdG9ncmFtKGFlcyhjYXJhdCksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDAuMDEpICsKICAgIGZhY2V0X3dyYXAofiBjdXQsCiAgICAgICAgICAgICAgIHNjYWxlcyA9ICJmcmVlX3kiLAogICAgICAgICAgICAgICBuY29sID0gMSkKYGBgCgpMYXJnZXIgZGlhbW9uZHMgaGF2ZSBhIGhpZ2hlciBwcmljZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGRpYW1vbmRzLCBhZXMoeCA9IGNhcmF0LCB5ID0gcHJpY2UpKSArCiAgICBnZW9tX3BvaW50KCkKYGBgCgpUaGVyZSBpcyBhIGxvdCBvZiBvdmVyLXBsb3R0aW5nLCBzbyBhIGdvb2Qgb3Bwb3J0dW5pdHkgdG8gdHJ5IHNvbWUgb2YgdGhlCnRlY2huaXF1ZXMgd2UgaGF2ZSBsZWFybmVkLgoKU29tZSBleHBsb3JhdGlvbnM6CgpSZWR1Y2VkIHBvaW50IHNpemU6CmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcCA8LSBnZ3Bsb3QoZGlhbW9uZHMsCiAgICAgICAgICAgIGFlcyh4ID0gY2FyYXQsIHkgPSBwcmljZSkpCnAgKyBnZW9tX3BvaW50KHNpemUgPSAwLjEpCmBgYAoKUmVkdWNlZCBwb2ludCBzaXplIGFuZCBhbHBoYSBsZXZlbDoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwICsgZ2VvbV9wb2ludChzaXplID0gMC4xLCBhbHBoYSA9IDAuMSkKYGBgCgpUcnkgbG9nIHNjYWxlIGZvciBwcmljZToKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwICsgZ2VvbV9wb2ludChzaXplID0gMC4xLCBhbHBoYSA9IDAuMSkgKwogICAgc2NhbGVfeV9sb2cxMCgpCmBgYAoKTG9nIHNjYWxlIGZvciBib3RoOgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgKyBnZW9tX3BvaW50KHNpemUgPSAwLjEsIGFscGhhID0gMC4xKSArCiAgICBzY2FsZV94X2xvZzEwKCkgKwogICAgc2NhbGVfeV9sb2cxMCgpCmBgYAoKQWRkIGEgc21vb3RoOgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgKyBnZW9tX3BvaW50KHNpemUgPSAwLjEsIGFscGhhID0gMC4xKSArCiAgICBnZW9tX3Ntb290aCgpICsKICAgIHNjYWxlX3hfbG9nMTAoKSArCiAgICBzY2FsZV95X2xvZzEwKCkKYGBgCgpTZXBhcmF0ZSBzbW9vdGhzIGZvciBlYWNoIGN1dDoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwICsgZ2VvbV9wb2ludChzaXplID0gMC4xLCBhbHBoYSA9IDAuMSkgKwogICAgZ2VvbV9zbW9vdGgoYWVzKGNvbG9yID0gY3V0KSkgKwogICAgc2NhbGVfeF9sb2cxMCgpICsKICAgIHNjYWxlX3lfbG9nMTAoKQpgYGAKCkV4cGxvcmluZyBhIHNhbXBsZToKCmBgYHtyfQpkNTAwIDwtIHNhbXBsZV9uKGRpYW1vbmRzLCA1MDApCmBgYApEaXN0cmlidXRpb24gb2YgYGN1dGAgaW4gdGhlIHNhbXBsZToKCmBgYHtyLCBmaWcuaGVpZ2h0ID0gNCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkNTAwLCBhZXMoeCA9IGN1dCkpICsKICAgIGdlb21fYmFyKCkKYGBgCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkNTAwLCBhZXMoeCA9IGNhcmF0LCB5ID0gcHJpY2UpKSArCiAgICBnZW9tX3BvaW50KCkKYGBgCgpZb3UgY2FuIGFsc28gdGFrZSBhIF9zdHJhdGlmaWVkIHNhbXBsZV8gc3RyYXRpZmllZCBvbiBjdXQgdXNpbmcKYGdyb3VwX2J5YCwgYHNhbXBsZV9mcmFjYCwgYW5kIGB1bmdyb3VwYC4KCkV4cGxvcmF0aW9ucyB1c2luZyBmYWNldHM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAwIDwtIGdncGxvdChkaWFtb25kcywgYWVzKHggPSBjYXJhdCwgeSA9IHByaWNlKSkKZE5vQ3V0IDwtIG11dGF0ZShkaWFtb25kcywgY3V0ID0gTlVMTCkKcDEgPC0gcDAgKyBnZW9tX3BvaW50KGFscGhhID0gMC4wMSwgY29sb3IgPSAiZ3JleSIsIGRhdGEgPSBkTm9DdXQpCnAgPC0gcDEgKyBnZW9tX3BvaW50KGNvbG9yID0gInJlZCIsIHNpemUgPSAxLCBhbHBoYSA9IDAuMDUpCiMjIHAgKyBmYWNldF93cmFwKH4gY3V0KQpwICsgZmFjZXRfd3JhcCh+IGN1dCkgKyBzY2FsZV94X2xvZzEwKCkgKyBzY2FsZV95X2xvZzEwKCkKYGBgCgpGYWNldHMgd2l0aCBhIHNhbXBsZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcDUwMCA8LSBwMSArCiAgICBnZW9tX3BvaW50KGRhdGEgPSBkNTAwLAogICAgICAgICAgICAgICBjb2xvciA9ICJyZWQiLAogICAgICAgICAgICAgICBzaXplID0gMSkKIyMgcDUwMAojIyBwNTAwICsgZmFjZXRfd3JhcCh+IGN1dCkKcDUwMCArCiAgICBmYWNldF93cmFwKH4gY3V0KSArCiAgICBzY2FsZV94X2xvZzEwKCkgKwogICAgc2NhbGVfeV9sb2cxMCgpCmBgYAoKTXV0ZWQgZGF0YSB3aXRoIHNtb290aHM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAxICsKICAgIGdlb21fc21vb3RoKGFlcyhjb2xvciA9IGN1dCksCiAgICAgICAgICAgICAgICBzZSA9IEZBTFNFKSArCiAgICBzY2FsZV94X2xvZzEwKCkgKwogICAgc2NhbGVfeV9sb2cxMCgpCmBgYAoKQ29uZGl0aW9uaW5nLCBgY2FyYXRgIHZhbHVlcyBuZWFyIDEsIDEuNSwgb3IgMjoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZHJuZCA8LSBtdXRhdGUoZGlhbW9uZHMsCiAgICAgICAgICAgICAgIGNybmQgPSByb3VuZCgyICogY2FyYXQpIC8gMikKIyMgTG9vayBhdCBhIGJhciBjaGFydCBvZiBjb3VudChkcm5kLCBjcm5kKQojIyBEcm9wIGhpZ2hlciBjYXJhdCB2YWx1ZXMgZnJvbSBkZW5zaXR5IHJpZGdlcwojIyBtYXAgY3V0IHRvIGNvbG9yIG9yIGZpbGwgKG5lZWQgdG8gdXNlIGdyb3VwID0gaW50ZXJhY3Rpb24oY3JuZCwgY3V0KSkKIyMgdHJ5IGxvZyBzY2FsZSBmb3IgcHJpY2UKZmlsdGVyKGRybmQsCiAgICAgICBjcm5kIDw9IDIsIGNybmQgPj0gMSwKICAgICAgIGNhcmF0ID49IGNybmQsIGNhcmF0IDw9IGNybmQgKyAwLjEpIHw+CiAgICBnZ3Bsb3QoYWVzKHggPSBwcmljZSwgeSA9IGN1dCkpICsKICAgIGdlb21fZGVuc2l0eV9yaWRnZXMocXVhbnRpbGVfbGluZXMgPSBUUlVFLAogICAgICAgICAgICAgICAgICAgICAgICBxdWFudGlsZXMgPSAyKSArCiAgICBmYWNldF93cmFwKH5jcm5kLCBuY29sID0gMSkKYGBgCgo8IS0tCkZvY3VzIG9uIGNhcmF0IHZhbHVlcyBuZWFyIG9uZToKCmBgYHtyLCBldmFsID0gRkFMU0V9CmZpbHRlcihkaWFtb25kcywgY2FyYXQgPj0gMC45NSwgY2FyYXQgPCAxLjA1KSB8PgogICAgZ2dwbG90KGFlcyh4ID0gY3V0LCB5ID0gcHJpY2UpKSArCiAgICBnZW9tX3Zpb2xpbihzY2FsZSA9ICJjb3VudCIsIGRyYXdfcXVhbnRpbGVzID0gMC41KQojIyBUcnkgZGVuc2l0eSByaWRnZXMKYGBgCi0tPgoKCiMjIFJlYWRpbmcKCkNoYXB0ZXIgW19WaXN1YWxpemluZyBhc3NvY2lhdGlvbnMgYW1vbmcgdHdvIG9yIG1vcmUgcXVhbnRpdGF0aXZlCiAgdmFyaWFibGVzX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6L3Zpc3VhbGl6aW5nLWFzc29jaWF0aW9ucy5odG1sKQogIGluIFtfRnVuZGFtZW50YWxzIG9mIERhdGEKICBWaXN1YWxpemF0aW9uX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6LykuCgoKIyMgRXhlcmNpc2VzCgoxLiBBIHBsb3Qgb2YgYXJyaXZhbCBkZWxheSBhZ2FpbnN0IGRlcGFydHVyZSBkZWxheSBmb3IgdGhlIE5ZQyBmbGlnaHQKICAgZGF0YSBzaG93cyBhIGxvdCBvZiBvdmVyLXBsb3R0aW5nLCBldmVuIGZvciBhIDEwJSBzYW1wbGUuCgogICAgYGBge3J9CiAgICBsaWJyYXJ5KGRwbHlyKQogICAgbGlicmFyeShnZ3Bsb3QyKQogICAgbGlicmFyeShueWNmbGlnaHRzMTMpCiAgICBmbCA8LSBmaWx0ZXIoZmxpZ2h0cywgZGVwX2RlbGF5IDwgMTIwKSB8PgogICAgICAgIHNhbXBsZV9mcmFjKDAuMSkKICAgIHAgPC0gZ2dwbG90KGZsLCBhZXMoeCA9IGRlcF9kZWxheSwgYXJyX2RlbGF5KSkgKwogICAgICAgIGdlb21fcG9pbnQoKQogICAgcAogICAgYGBgCgogICAgVGhpcyBtYXNrcyB0aGUgZmFjdCB0aGF0IHRocmVlIHF1YXJ0ZXJzIG9mIHRoZSBmbGlnaHRzIGluIHRoaXMKICAgIHNhbXBsZSBoYXZlIGRlcGFydHVyZSBkZWxheXMgb2YgbGVzcyB0aGFuIDEwCiAgICBtaW51dGVzLiBTdXBlcmltcG9zaW5nIGRlbnNpdHkgY29udG91cnMgaXMgb25lIHdheSB0byBhZGRyZXNzIHRoaXMKICAgIGlzc3VlLgoKICAgIFdoaWNoIG9mIHRoZSBmb2xsb3dpbmcgYWRkcyBmb3VyIHJlZCBkZW5zaXR5IGNvbnRvdXJzIHRvIHRoZSBwbG90PwoKICAgIGEuIGBwICsgZ2VvbV9kZW5zaXR5XzJkKGNvbG9yID0gInJlZCIpYAogICAgYi4gYHAgKyBnZW9tX2RlbnNpdHlfMmQoYmlucyA9IDQsIGNvbG9yID0gInJlZCIpYAogICAgYy4gYHAgKyBnZW9tX2hleChiaW5zID0gNSlgCiAgICBkLiBgcCArIGdlb21fZGVuc2l0eV8yZChiaW5zID0gNSlgCgoyLiBUaGUgYGRpYW1vbmRzYCBkYXRhIHNldCBpcyBsYXJnZSBlbm91Z2ggZm9yIGEgc2NhdHRlciBwbG90IG9mCiAgICBgcHJpY2VgIGFnYWluc3QgYGNhcmF0YCB0byBzdWZmZXIgZnJvbSBhIHNpZ25pZmljYW50IGFtb3VudCBvZgogICAgb3Zlci1wbG90dGluZy4gIFdpdGggYHBgIGNyZWF0ZWQgYXMKCiAgICBgYGB7cn0KICAgIGxpYnJhcnkoZ2dwbG90MikKICAgIHAgPC0gZ2dwbG90KGRpYW1vbmRzLCBhZXMoeCA9IGNhcmF0LCB5ID0gcHJpY2UpKQogICAgYGBgCgogICAgd2hpY2ggb2YgdGhlIGZvbGxvd2luZyBpcyB0aGUgYmVzdCBjaG9pY2UgdG8gYWRkcmVzcyB0aGUKICAgIG92ZXItcGxvdHRpbmcgaXNzdWU/CgogICAgYS4gYHAgKyBnZW9tX3BvaW50KClgCiAgICBiLiBgcCArIGdlb21fcG9pbnQoc2l6ZSA9IDAuNSlgCiAgICBjLiBgcCArIGdlb21fcG9pbnQoc2l6ZSA9IDAuMSwgYWxwaGEgPSAwLjEpYAogICAgZC4gYHAgKyBnZW9tX3BvaW50KHBvc2l0aW9uID0gImppdHRlciIpYAoKCjMuICBDb25zaWRlciB0aGUgY29kZQo8IS0tICMjIG5vbGludCBzdGFydCAtLT4KICAgIGBgYHtyLCBldmFsID0gRkFMU0V9CiAgICBsaWJyYXJ5KGRwbHlyKQogICAgbGlicmFyeShnZ3Bsb3QyKQogICAgZmlsdGVyKGRpYW1vbmRzLCBjYXJhdCA8IDMpIHw+CiAgICAgICAgbXV0YXRlKGNybmQgPSByb3VuZChjYXJhdCkpIHw+CiAgICAgICAgZmlsdGVyKC0tLSkgfD4KICAgICAgICBnZ3Bsb3QoYWVzKHggPSBwcmljZSwgeSA9IGNybmQsIGdyb3VwID0gY3JuZCkpICsKICAgICAgICBnZW9tX2RlbnNpdHlfcmlkZ2VzKCkKICAgIGBgYAo8IS0tIyMgbm9saW50IGVuZCAtLT4KCiAgICBXaGljaCByZXBsYWNlbWVudCBmb3IgYC0tLWAgcHJvZHVjZXMgYSBwbG90IHNob3dpbmcgdGhlCiAgICBjb25kaXRpb25hbCBkZW5zaXR5IG9mIGBwcmljZWAgZ2l2ZW4gYGNhcmF0YCBmb3IgYGNhcmF0YCB2YWx1ZXMKICAgIG5lYXIgb25lIGFuZCB0aGUgY29uZGl0aW9uYWwgZGVuc2l0eSBvZiBgcHJpY2VgIGdpdmVuIGBjYXJhdGAgZm9yCiAgICBgY2FyYXRgIHZhbHVlcyBuZWFyIHR3bz8KCiAgICBhLiBgYWJzKGNhcmF0IC0gY3JuZCkgPCAwLjFgCiAgICBiLiBgY2FyYXQgPCAwLjFgCiAgICBjLiBgYWJzKGNybmQpIDwgMWAKICAgIGQuIGBjYXJhdCArIGNybmQgPCAyYAo=