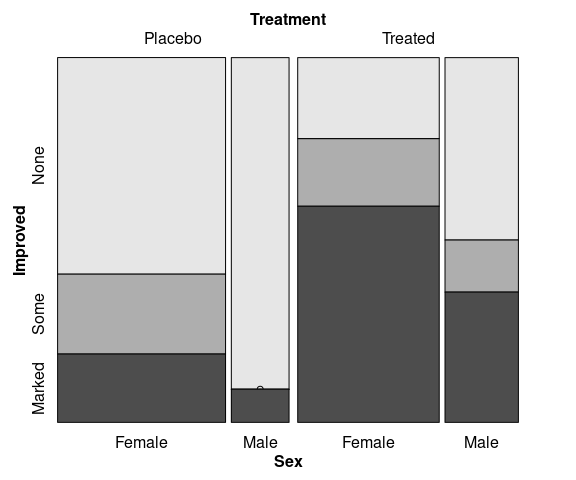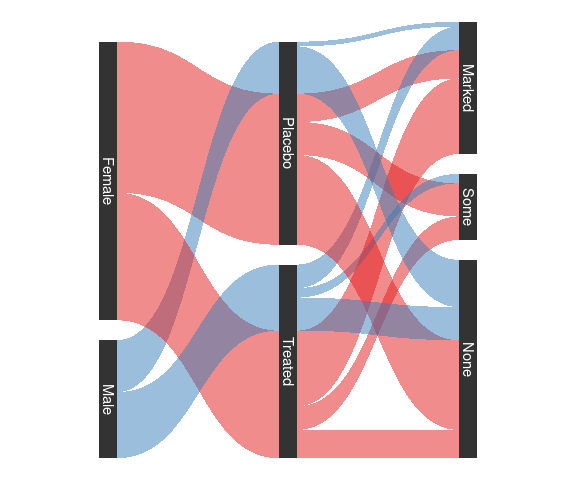Categorical Data
Categorical data can be
nominal, qualitative
ordinal
For visualization, the main difference is that ordinal data suggests a particular display order.
Purely categorical data can come in a range of formats.
The most common are
Raw Data
Raw data for a survey of individuals that records hair color, eye color, and gender of 592 individuals might look like this:
head(raw)
## Hair Eye Sex
## 1 Brown Blue Male
## 2 Brown Brown Male
## 3 Brown Hazel Male
## 4 Blond Green Female
## 5 Brown Brown Female
## 6 Brown Hazel Male
Aggregated Data
One way to aggregate raw categorical data is to use count from dplyr:
library(dplyr)
agg <- count(raw, Hair, Eye, Sex) |>
as_tibble()
agg
## # A tibble: 32 × 4
## Hair Eye Sex n
## <fct> <fct> <fct> <int>
## 1 Black Brown Male 32
## 2 Black Brown Female 36
## 3 Black Blue Male 11
## 4 Black Blue Female 9
## 5 Black Hazel Male 10
## 6 Black Hazel Female 5
## 7 Black Green Male 3
## 8 Black Green Female 2
## 9 Brown Brown Male 53
## 10 Brown Brown Female 66
## # ℹ 22 more rows
Cross-Tabulated Data
Cross-tabulated data can be produced from aggregate data using xtabs:
xtabs(n ~ Hair + Eye + Sex, data = agg)
## , , Sex = Male
##
## Eye
## Hair Brown Blue Hazel Green
## Black 32 11 10 3
## Brown 53 50 25 15
## Red 10 10 7 7
## Blond 3 30 5 8
##
## , , Sex = Female
##
## Eye
## Hair Brown Blue Hazel Green
## Black 36 9 5 2
## Brown 66 34 29 14
## Red 16 7 7 7
## Blond 4 64 5 8Cross-tabulated data can be produced from raw data using table:
xtb <- table(raw)
xtb
## , , Sex = Male
##
## Eye
## Hair Brown Blue Hazel Green
## Black 32 11 10 3
## Brown 53 50 25 15
## Red 10 10 7 7
## Blond 3 30 5 8
##
## , , Sex = Female
##
## Eye
## Hair Brown Blue Hazel Green
## Black 36 9 5 2
## Brown 66 34 29 14
## Red 16 7 7 7
## Blond 4 64 5 8Both raw and aggregate data in this example are in tidy form; the cross-tabulated data is not.
Cross-tabulated data on \(p\) variables is arranged in a \(p\) -way array.
The cross-tabulated data can be converted to the tidy aggregate form using as.data.frame:
class(xtb)
## [1] "table"
head(as.data.frame(xtb))
## Hair Eye Sex Freq
## 1 Black Brown Male 32
## 2 Brown Brown Male 53
## 3 Red Brown Male 10
## 4 Blond Brown Male 3
## 5 Black Blue Male 11
## 6 Brown Blue Male 50The variable xtb corresponds to the data set HairEyeColor in the datasets package,
Working With Categorical Variables
Categorical variables are usually represented as:
character vectors
factors.
Some advantages of factors:
more control over ordering of levels
levels are preserved when forming subsets
levels can reflect possible values not present in the data
Most plotting and modeling functions will convert character vectors to factors with levels ordered alphabetically.
Some standard R functions for working with factors include
factor creates a factor from another type of variablelevels returns the levels of a factorreorder changes level order to match another variablerelevel moves a particular level to the first position as a base linedroplevels removes levels not in the variable.
The tidyverse package forcats adds some more tools, including
fct_inorder creates a factor with levels ordered by first appearancefct_infreq orders levels by decreasing frequencyfct_rev reverses the levelsfct_recode changes factor levelsfct_relevel moves one or more levelsfct_c merges two or more factorsfct_collapse merge some factor levels
Bar Charts For Frequencies
Basics
A bar chart is often used to show the frequencies of a categorical variable.
By default, geom_bar uses stat = "count" and maps its result to the y aesthetic.
This is suitable for raw data:
thm <- theme_minimal() +
theme(text = element_text(size = 16))
ggplot(raw) +
geom_bar(aes(x = Hair),
fill = "deepskyblue3") +
thm
For a nominal variable it is often better to order the bars by decreasing frequency:
library(forcats)
ggplot(mutate(raw,
Hair = fct_infreq(Hair))) +
geom_bar(aes(x = Hair),
fill = "deepskyblue3") +
thm
If the data have already been aggregated, then you need to either
ggplot(agg) +
geom_col(aes(x = Hair,
y = n),
fill = "deepskyblue3") +
thm
For aggregated data, reordering can be based on the computed counts using
agg_ord <-
mutate(agg,
Hair = reorder(Hair, -n, sum))ggplot(agg_ord) +
geom_col(aes(x = Hair,
y = n),
fill = "deepskyblue3") +
thm
Adding a Grouping Variable
Mapping the Eye variable to fill in ggplot produces a stacked bar chart .
An alternative, specified with position = "dodge", is a side by side bar chart, or a clustered bar chart.
For the side by side chart in particular it may be useful to also reorder the Eye color levels.
ecols <- c(Brown = "brown4",
Blue = "blue2",
Hazel = "darkgoldenrod3",
Green = "green4")
agg_ord <-
mutate(agg,
Hair = reorder(Hair, -n, sum),
Eye = reorder(Eye, -n, sum))
p1 <- ggplot(agg_ord) +
geom_col(aes(x = Hair,
y = n,
fill = Eye)) +
scale_fill_manual(values = ecols) +
thm
p2 <- ggplot(agg_ord) +
geom_col(aes(x = Hair,
y = n,
fill = Eye),
position = "dodge") +
scale_fill_manual(values = ecols) +
thm
(p1 + guides(fill = "none")) | p2
Faceting can be used to bring in additional variables:
p1 + facet_wrap(~ Sex)
The counts shown here may not be the most relevant features for understanding the joint distributions of these variables.
Pie Charts and Doughnut Charts
Pie charts go by many different names (from a Twitter thread ):
Pie charts can be viewed as stacked bar charts in polar coordinates:
hcols <- c(Black = "black", Brown = "brown4",
Red = "brown1", Blond = "lightgoldenrod1")
p1 <- ggplot(agg_ord) +
geom_col(aes(x = 1, y = n, fill = Hair), position = "fill") +
coord_polar(theta = "y") +
scale_fill_manual(values = hcols) +
thm
p2 <- ggplot(agg_ord) +
geom_col(aes(x = Hair, y = n, fill = Hair)) +
scale_fill_manual(values = hcols) +
thm
(p1 + guides(fill = "none")) | p2
The axes and grid lines are not helpful for the pie chart and can be removed with some theme settings.
Using faceting we can also separately show the distributions for men and women:
pie_thm <- thm +
theme(axis.title = element_blank(),
axis.text = element_blank(),
axis.ticks = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.border = element_blank())
p3 <- p1 + facet_wrap(~ Sex) + pie_thm
p3
Doughnut charts are a variant that has recently become popular in the media:
p4 <- p3 + xlim(0, 1.5)
p4
The center is often used for annotation:
p4 + geom_text(aes(x = 0, y = 0, label = Sex), size = 5) +
theme(strip.background = element_blank(),
strip.text = element_blank())
An alternative to the polar coordinates approach uses geom_arc_bar and stat_pie from package ggforce:
library(ggforce)
arrange(agg_ord, desc(Hair)) |>
ggplot(aes(x0 = 0, y0 = 0, r0 = 0, r = 1, amount = n, fill = Hair)) +
geom_arc_bar(stat = "pie", color = NA) +
coord_fixed() +
scale_fill_manual(values = hcols) +
pie_thm +
facet_wrap(~ Sex)
For doughnut charts:
arrange(agg_ord, desc(Hair)) |>
ggplot(aes(x0 = 0, y0 = 0, r0 = 0.4, r = 1, amount = n, fill = Hair)) +
geom_arc_bar(stat = "pie", color = NA) +
geom_text(aes(x = 0, y = 0, label = Sex), size = 5) +
coord_fixed() +
scale_fill_manual(values = hcols) +
pie_thm +
theme(strip.background = element_blank(),
strip.text = element_blank()) +
facet_wrap(~ Sex)
Some Notes
Pie charts are effective for judging part/whole relationships.
Pie charts can be effective for comparing proportions to
Pie charts are not very effective for comparing proportions to each other.
3D pie charts are popular and a very bad idea. An example (Fig. 6.61 ) from Andy Kirk’s book (2016), Data Visualization: A Handbook for Data Driven Design
Pie charts are widely used for political data.
With the right ordering, pie charts are very good at showing which coalitions of parties can form a majority.
When no one candidate earns a majority of the votes, pie charts do not show which candidate has earned a plurality very well.
Good orientation and factor ordering can help.
elect <- geofacet::election |>
group_by(candidate) |>
summarize(votes = sum(votes))
p1 <- ggplot(elect) +
geom_col(aes(x = 1, y = votes, fill = candidate), position = "fill") +
coord_polar(theta = "y", start = -1) +
xlim(c(-0.5, 1.5)) +
scale_fill_manual(values = c(Trump = scales::muted("red", 50, 80),
Clinton = scales::muted("blue", 50, 70),
Other = "grey")) +
pie_thm
p2 <- mutate(elect,
candidate = factor(candidate,
c("Clinton", "Other", "Trump"))) |>
ggplot() +
geom_col(aes(x = 1, y = votes, fill = candidate), position = "fill") +
coord_polar(theta = "y") +
xlim(c(-0.5, 1.5)) +
scale_fill_manual(values = c(Trump = scales::muted("red", 50, 80),
Clinton = scales::muted("blue", 50, 70),
Other = "grey")) +
pie_thm
p3 <- ggplot(elect) +
geom_col(aes(x = candidate,
y = 100 * (votes / sum(votes)),
fill = candidate)) +
scale_fill_manual(values = c(Trump = scales::muted("red", 50, 80),
Clinton = scales::muted("blue", 50, 70),
Other = "grey")) +
labs(y = "percent") +
thm +
theme(axis.text.x = element_blank(),
axis.title.x = element_blank())
(p1 + guides(fill = "none")) + (p2 + guides(fill = "none")) + p3
Some Alternatives
Stacked Bar Charts
Stacked bar charts with equal heights, or filled bar charts, are an alternative for representing part-whole relationships.
ggplot(agg) +
geom_col(aes(x = Sex, y = n, fill = Hair), position = "fill") +
scale_fill_manual(values = hcols) +
thm
Waffle Charts
Another alternative is a waffle chart , sometimes also called a square pie chart .
The waffle
Currently the development version on GitHub is needed for the following examples.
Showing the counts:
library(waffle)
stopifnot(packageVersion("waffle") >= "1.0.1")
ggplot(arrange(agg, Hair), aes(values = n, fill = Hair)) +
geom_waffle(n_rows = 18, flip = TRUE, color = "white", size = 0.33,
na.rm = FALSE) +
coord_equal() +
facet_wrap(~ Sex) +
scale_fill_manual(values = hcols) +
theme_minimal() +
theme_enhance_waffle()
Showing the proportions:
round_pct <- function(n) {
pct <- 100 * (n / sum(n))
nn <- floor(pct)
if (sum(nn) < 100) {
rem <- pct - nn
idx <- sort(order(rem), decreasing = TRUE)[seq_len(100 - sum(nn))]
nn[idx] <- nn[idx] + 1
}
nn
}
group_by(agg, Sex) |>
mutate(pct = round_pct(n)) |>
ungroup() |>
ggplot(aes(values = pct, fill = Hair)) +
geom_waffle(n_rows = 10, flip = TRUE, color = "white", size = 0.33,
na.rm = FALSE) +
coord_equal() +
facet_wrap(~ Sex) +
scale_fill_manual(values = hcols) +
theme_minimal() +
theme_enhance_waffle()
Population Pyramids
Bar charts for two groups can be shown back to back.
mutate(agg, Hair = reorder(Hair, n, sum)) |>
ggplot(aes(x = ifelse(Sex == "Male", n, -n),
y = Hair,
fill = Sex)) +
geom_col() +
xlab("Count") +
thm
This is often used for showing age distributions by sex for populations; the result is called a population pyramid
Age distribution data for many countries and years is available from a Census Bureau website .
Data files for 2020 for Germany and Nigeria are available locally.
if (! file.exists("germany-2020.csv"))
download.file("https://stat.uiowa.edu/~luke/data/germany-2020.csv",
"germany-2020.csv")
if (! file.exists("nigeria-2020.csv"))
download.file("https://stat.uiowa.edu/~luke/data/nigeria-2020.csv",
"nigeria-2020.csv")
gm_pop <- read.csv("germany-2020.csv", skip = 1) |>
filter(Age != "Total") |>
mutate(Age = fct_inorder(Age))
ni_pop <- read.csv("nigeria-2020.csv", skip = 1) |>
filter(Age != "Total") |>
mutate(Age = fct_inorder(Age))Combining the data sets allows a side by side comparison of the counts:
library(tidyr)
pop2 <-
bind_rows(mutate(gm_pop, Country = "Germany"),
mutate(ni_pop, Country = "Nigeria")) |>
select(Age,
Male = Male.Population,
Female = Female.Population, Country) |>
pivot_longer(Male : Female,
names_to = "Sex",
values_to = "n")
ggplot(pop2) +
geom_col(aes(x = ifelse(Sex == "Male", n, -n),
y = Age,
fill = Sex)) +
facet_wrap(~ Country) +
scale_x_continuous(
labels = function(n) scales::comma(abs(n))) +
xlab("Count") +
thm +
theme(legend.position = "top")
The different shapes are evident, but are harder to see than they could be because of the difference in total population:
group_by(pop2, Country) |>
summarize(Population = sum(n)) |>
ungroup() |>
mutate(Population = scales::comma(Population)) |>
knitr::kable(format = "html", align = "lr") |>
kableExtra::kable_styling(full_width = FALSE)
Country
Population
Germany
80,159,662
Nigeria
214,028,302
Using a group mutate we can compute sex/age group percentages within each country:
group_by(pop2, Country) |>
mutate(pct = 100 * n / sum(n)) |>
ungroup() |>
ggplot() +
geom_col(aes(x = ifelse(Sex == "Male", pct, -pct),
y = Age,
fill = Sex)) +
facet_wrap(~ Country) +
scale_x_continuous(
labels = function(x) scales::percent(abs(x / 100))) +
xlab("Percent") +
thm +
theme(legend.position = "top")
Multiple Categorical Variables
Visualizing the distribution of multiple categorical variables involves visualizing counts and proportions.
Distributions can be viewed as
When one variable (or several) can be viewed as a response and others as predictors then it is common to focus on the conditional distribution of the response given the predictors.
The most common approaches use variants of bar and area charts.
The resulting plots are often called mosaic plots
Two Data Sets
Hair and Eye Color
HairEyeColorDF <-
as.data.frame(HairEyeColor)
head(HairEyeColorDF)
## Hair Eye Sex Freq
## 1 Black Brown Male 32
## 2 Brown Brown Male 53
## 3 Red Brown Male 10
## 4 Blond Brown Male 3
## 5 Black Blue Male 11
## 6 Brown Blue Male 50Marginal distributions of the variables:
p1 <- ggplot(HairEyeColorDF) +
geom_col(aes(Sex, Freq), fill = "deepskyblue3") +
thm
p2 <- mutate(HairEyeColorDF, Hair = reorder(Hair, -Freq, sum)) |>
ggplot() +
geom_col(aes(Hair, Freq), fill = "deepskyblue3") +
thm
p3 <- ggplot(HairEyeColorDF) +
geom_col(aes(Eye, Freq), fill = "deepskyblue3") +
thm
p1 | p2 | p3
Arthritis Data
The vcd package includes the data frame Arthritis with several variables for 84 patients in a clinical trial for a treatment for rheumatoid arthritis.
data(Arthritis, package = "vcd")
head(Arthritis)
## ID Treatment Sex Age Improved
## 1 57 Treated Male 27 Some
## 2 46 Treated Male 29 None
## 3 77 Treated Male 30 None
## 4 17 Treated Male 32 Marked
## 5 36 Treated Male 46 Marked
## 6 23 Treated Male 58 Marked
The Improved variable is the response.
The predictors are Treatment, Sex, and Age.
Counts for the categorical predictors:
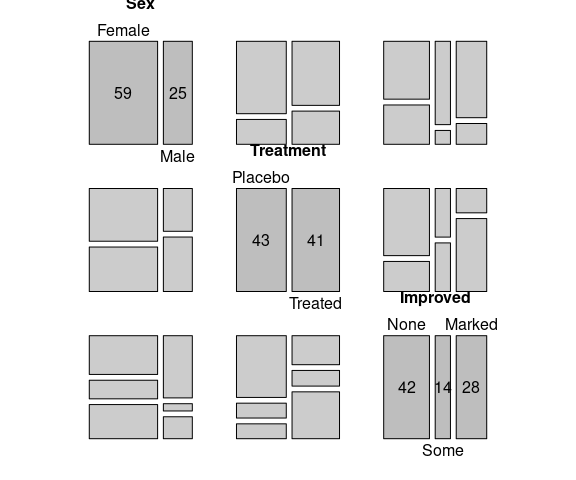
xtabs(~ Sex, Arthritis)
## Sex
## Female Male
## 59 25xtabs(~ Treatment, Arthritis)
## Treatment
## Placebo Treated
## 43 41xtabs(~ Treatment + Sex, data = Arthritis)
## Sex
## Treatment Female Male
## Placebo 32 11
## Treated 27 14Joint distribution of the predictors:
ggplot(Arthritis) +
geom_histogram(aes(x = Age),
binwidth = 10,
fill = "deepskyblue3",
color = "black") +
facet_grid(Treatment ~ Sex) +
thm
Conditional distribuiton of age, given sex and treatment:
ggplot(Arthritis) +
geom_histogram(aes(x = Age,
y = after_stat(density)),
binwidth = 10,
fill = "deepskyblue3",
color = "black") +
facet_grid(Treatment ~ Sex) +
thm
Bar Charts
Hair and Eye Color
Default bar charts show the individual count or joint proportions.
For the hair-eye color aggregated data counts:
ggplot(HairEyeColorDF) +
geom_col(aes(x = Eye, y = Freq, fill = Sex)) +
facet_wrap(~ Hair) +
thm
Joint proportions:
ggplot(mutate(HairEyeColorDF, Prop = Freq / sum(Freq))) +
geom_col(aes(x = Eye, y = Prop, fill = Sex)) +
facet_wrap(~ Hair) +
thm
Showing conditional distributions requires computing proportions within groups.
For the joint conditional distribution of sex and eye color given hair color:
group_by(HairEyeColorDF, Hair) |>
mutate(Prop = Freq / sum(Freq)) |>
ungroup() |>
ggplot() +
geom_col(aes(x = Eye, y = Prop, fill = Sex)) +
facet_wrap(~ Hair) +
thm
It is easier to compare the skewness of the eye color distributions for black, brown, and red hair.
Assessing the proportion of females or males withing the different groups is possible but challenging since it requires relative length comparisons.
To more clearly see the that the proportion of females among subjects with blond hair and blue eyes is higher than for other hair/eye color combinations we can look at the conditional distribution of sex given hair and eye color.
group_by(HairEyeColorDF, Hair, Eye) |>
mutate(Prop = Freq / sum(Freq)) |>
ungroup() |>
ggplot() +
geom_col(aes(x = Eye,
y = Prop,
fill = Sex)) +
facet_wrap(~ Hair, nrow = 1) +
thm +
theme(axis.text.x =
element_text(angle = 45,
hjust = 1))
This plot can also be obtained using position = "fill".
ggplot(HairEyeColorDF) +
geom_col(aes(x = Eye,
y = Freq,
fill = Sex),
position = "fill") +
facet_wrap(~ Hair, nrow = 1) +
thm +
theme(axis.text.x =
element_text(angle = 45,
hjust = 1))One drawback: This visualization no longer shows that some of the hair/eye color combinations are more common than others.
Arthritis Data
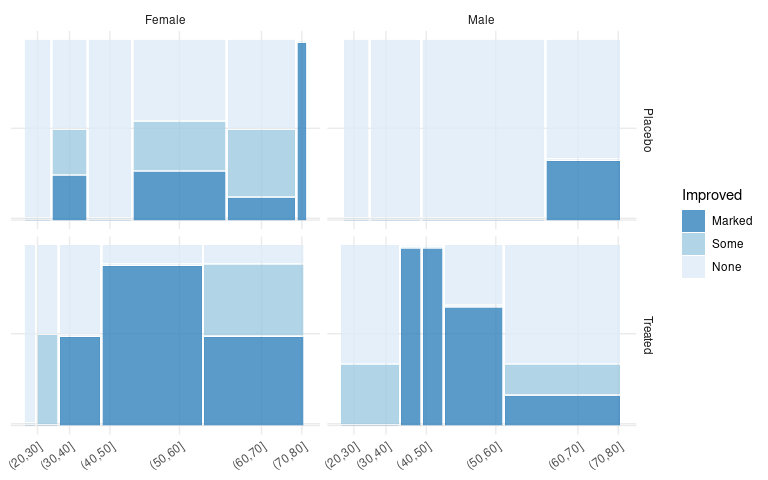
For the raw arthritis data, geom_bar computes the aggregate counts and produces a stacked bar chart by default:
p <- ggplot(Arthritis, aes(x = Sex,
fill = Improved)) +
facet_wrap(~ Treatment)
p + geom_bar() +
scale_fill_brewer(palette = "Blues") +
thm
Specifying position = "dodge" produces a side-by-side plot:
p + geom_bar(position = "dodge") +
scale_fill_brewer(palette = "Blues") +
thm
There are no cases of male patients on placebo reporting Some improvement, resulting in wider bars for the other options.
One way to produce a zero height bar:
library(tidyr)
comp_counts <-
count(Arthritis,
Treatment, Sex, Improved) |>
complete(Treatment, Sex, Improved,
fill = list(n = 0))
ggplot(comp_counts,
aes(x = Sex, y = n, fill = Improved)) +
geom_col(position = "dodge") +
facet_wrap(~ Treatment) +
scale_fill_brewer(palette = "Blues") +
thm
Another option is to use the preserve = "single" option with position_dodge.
p + geom_bar(position =
position_dodge(
preserve = "single")) +
scale_fill_brewer(palette = "Blues") +
thm
Showing conditional distributions of Improved given different levels of Treatment and Sex:
group_by(comp_counts, Treatment, Sex) |>
mutate(prop = n / sum(n)) |>
ungroup() |>
ggplot() +
geom_col(aes(x = Sex,
y = prop,
fill = Improved),
position = "dodge") +
facet_wrap(~ Treatment) +
scale_fill_brewer(palette = "Blues") +
thm
Stacked bar charts with height one are another option to make these conditional distributions easier to compare:
p + geom_bar(position = "fill") +
scale_fill_brewer(palette = "Blues") +
thm
Ordering of variables affects which comparisons are easier.
ggplot(Arthritis, aes(x = Treatment, fill = Improved)) +
geom_bar(position = "fill") +
scale_fill_brewer(palette = "Blues") +
thm +
facet_wrap(~ Sex)
Some notes:
The stacked bar chart is effective for two categories, and a few more if they are ordered.
Providing a visual indication of uncertainty in the estimates is a challenge. The standard errors in this case are around 0.1.
The proportions of each treatment group that are male or female could be encoded in the bar widths.
The resulting plot is called a spine plot .
Basic ggplot2 does not seem to make this easy.
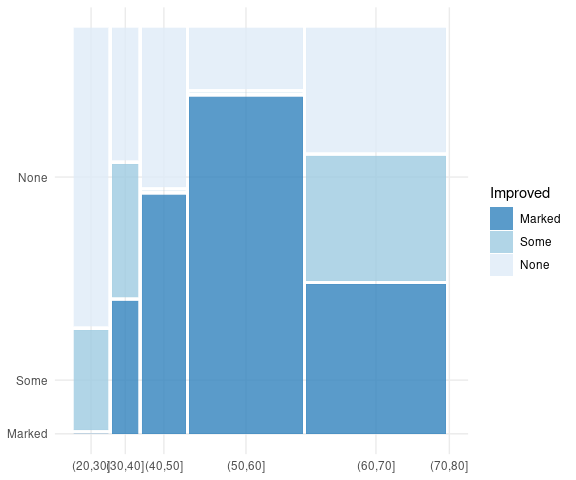
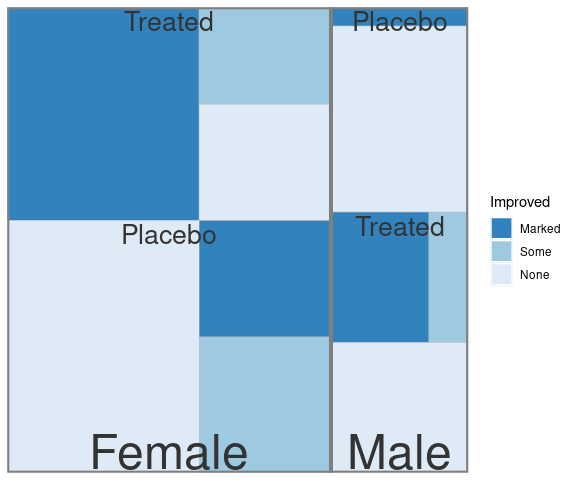
Spine Plots
Spine plots are a special case of mosaic plots
For a spine plot the proportions for the categories of a predictor variable are encoded in the bar widths.
The ggmosaic package provides support for mosaic plots in the ggplot framework. (It can be a little rough around the edges.)
Spine plots are provided by the base graphics function spineplot and the vcd function spine.
vcd plots are built on the grid graphics system, like lattice and ggplot2 graphics.
A spine plot for the distribution of Improved given Sex in the Treated group:
library(ggmosaic)
filter(Arthritis, Treatment == "Treated") |>
mutate(Improved = fct_rev(Improved)) |>
ggplot() +
geom_mosaic(aes(x = product(Sex),
fill = Improved)) +
scale_fill_brewer(palette = "Blues",
direction = -1,
guide = guide_legend(reverse = TRUE)) +
facet_wrap(~ Treatment) +
thm + labs(x = "", y = "Improved")
Spine plots for Treatment groups using faceting:
library(ggmosaic)
mutate(Arthritis,
Improved = fct_rev(Improved)) |>
ggplot() +
geom_mosaic(aes(x = product(Sex),
fill = Improved)) +
scale_fill_brewer(palette = "Blues",
direction = -1,
guide = guide_legend(reverse = TRUE)) +
facet_wrap(~ Treatment) +
thm + labs(x = "", y = "Improved")
Spine plots for the arthritis data, faceted on Sex:
library(ggmosaic)
mutate(Arthritis,
Improved = fct_rev(Improved)) |>
ggplot() +
geom_mosaic(aes(x = product(Treatment),
fill = Improved)) +
scale_fill_brewer(palette = "Blues",
direction = -1,
guide = guide_legend(reverse = TRUE)) +
facet_wrap(~ Sex) +
thm + labs(x = "", y = "Improved")
For aggregate counts use the weight aesthetic:
mutate(HairEyeColorDF, Sex = fct_rev(Sex)) |>
ggplot() +
geom_mosaic(aes(weight = Freq,
x = product(Hair),
fill = Sex)) +
thm + labs(x = "Hair", y = "")
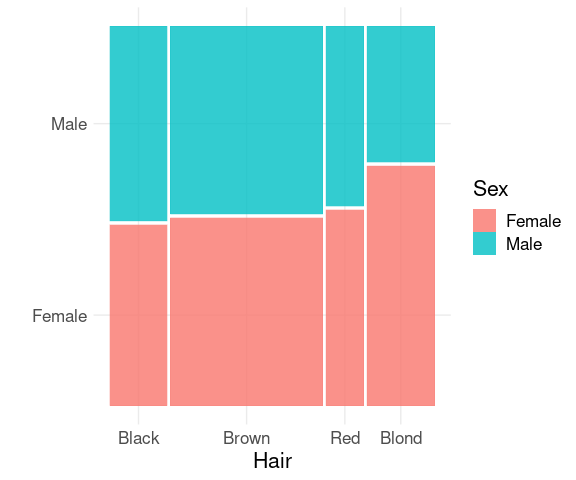
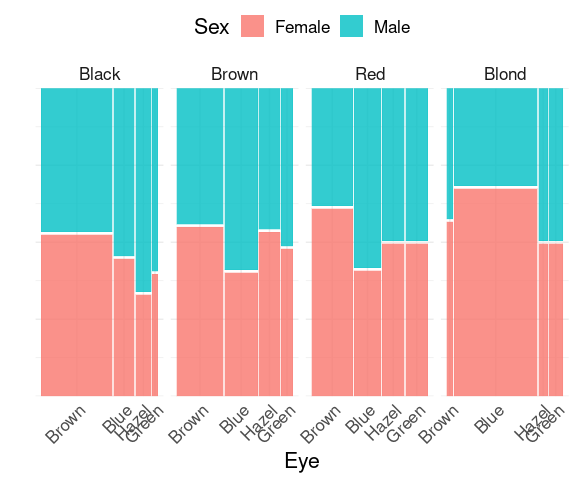
Spine plots of Sex within Eye color, faceted on Hair color:
mutate(HairEyeColorDF, Sex = fct_rev(Sex)) |>
ggplot() +
geom_mosaic(aes(weight = Freq,
x = product(Eye),
fill = Sex)) +
thm + labs(x = "Eye", y = "") +
facet_wrap(~ Hair,
nrow = 1,
scales = "free_x") +
theme(legend.position = "top",
axis.text.y = element_blank(),
axis.text.x =
element_text(angle = 45,
hjust = 1)) +
scale_y_continuous(expand = c(0, 0))
The relative sizes of the groups on the x (eye color) axis are shown within the facets.
The sizes of the faceted variable (hair color) groups are not reflected.
Double decker plots try to address this.
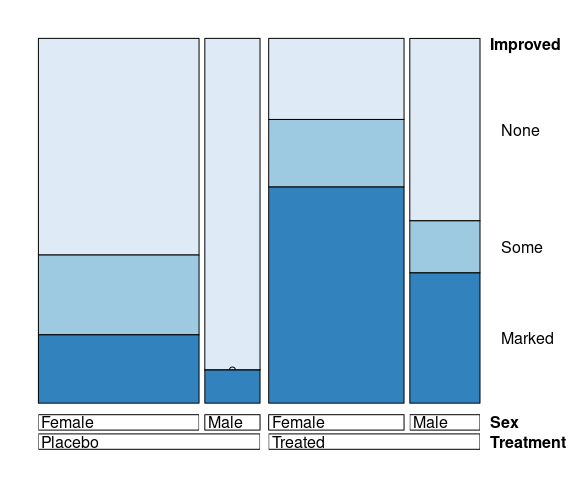
Doubledecker Plots
Doubledecker plots can be viewed as a generalization of spine plots to multiple predictors.
Package vcd provides the doubledecker function.
This function can use a formula interface.
arth_pal <-
RColorBrewer::brewer.pal(3, "Blues")
arth_gp <- grid::gpar(fill = arth_pal)
vcd::doubledecker(Improved ~ Treatment + Sex,
data = Arthritis,
gp = arth_gp,
margins = c(2, 5, 4, 2))
vcd::doubledecker(Improved ~ Sex + Treatment,
data = Arthritis,
gp = arth_gp,
margins = c(2, 5, 4, 2))
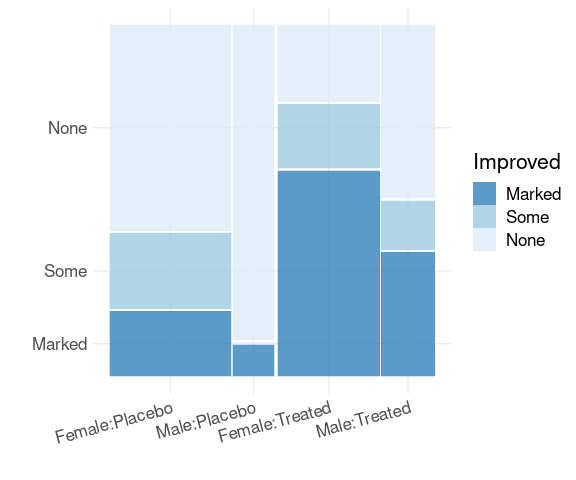
Using ggmosaic:
mutate(Arthritis,
Improved = fct_rev(Improved)) |>
ggplot() +
geom_mosaic(
aes(x = product(Sex, Treatment),
fill = Improved),
divider = ddecker()) +
scale_fill_brewer(palette = "Blues",
direction = -1,
guide = guide_legend(reverse = TRUE)) +
thm +
theme(axis.text.x =
element_text(angle = 15,
hjust = 1)) +
labs(x = "", y = "")
mutate(Arthritis,
Improved = fct_rev(Improved)) |>
ggplot() +
geom_mosaic(
aes(x = product(Treatment, Sex),
fill = Improved),
divider = ddecker()) +
scale_fill_brewer(palette = "Blues",
direction = -1,
guide = guide_legend(reverse = TRUE)) +
thm +
theme(axis.text.x =
element_text(angle = 15,
hjust = 1)) +
labs(x = "", y = "")
Another approach using the ggh4x
library(dplyr)
library(ggplot2)
library(ggh4x)
data(Arthritis, package = "vcd")
ggplot(Arthritis, aes(x = 0, fill = Improved)) +
geom_bar(position = "fill") +
scale_fill_brewer(palette = "Blues") +
facet_nested(~ Treatment + Sex) +
force_panelsizes(cols = count(Arthritis, Treatment, Sex)$n) +
labs(x = element_blank(), y = element_blank()) +
scale_x_continuous(expand = c(0, 0), breaks = NULL, labels = NULL) +
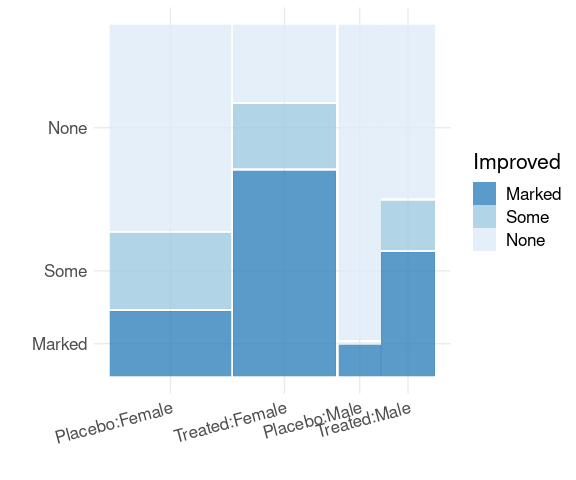
scale_y_continuous(expand = c(0, 0), breaks = NULL, labels = NULL)
library(dplyr)
library(ggplot2)
library(ggh4x)
data(Arthritis, package = "vcd")
ggplot(Arthritis, aes(x = 0, fill = Improved)) +
geom_bar(position = "fill") +
scale_fill_brewer(palette = "Blues") +
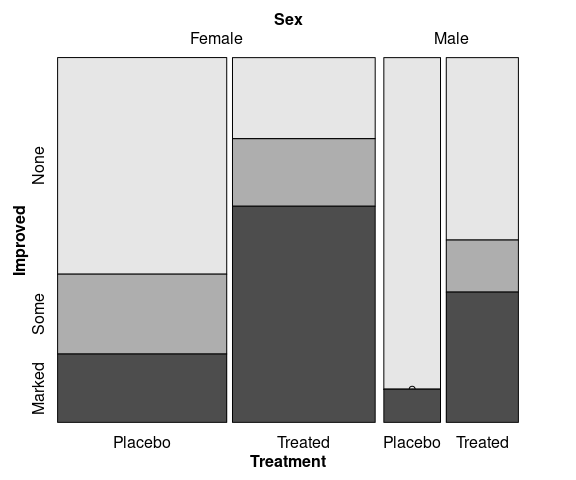
facet_nested(~ Sex + Treatment) +
force_panelsizes(cols = count(Arthritis, Sex, Treatment)$n) +
labs(x = element_blank(), y = element_blank()) +
scale_x_continuous(expand = c(0, 0), breaks = NULL, labels = NULL) +
scale_y_continuous(expand = c(0, 0), breaks = NULL, labels = NULL)
Mosaic Plots
Mosaic plots recursively partition the axes to represent counts of categorical variables as rectangles.
Both support a formula interface.
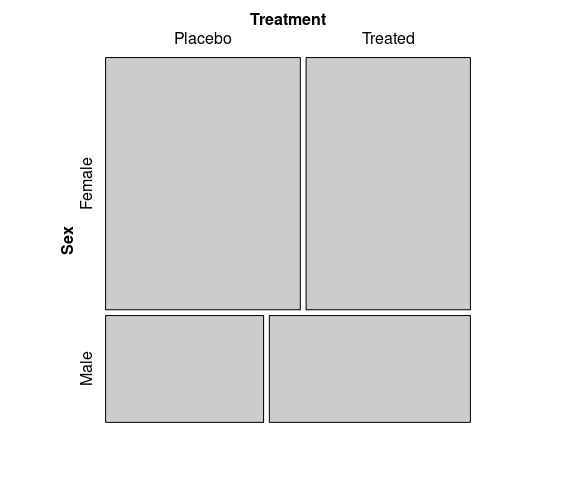
A Mosaic plot for the predictors Sex and Treatment:
vcd::mosaic(~ Sex + Treatment,
data = Arthritis)
Adding Improved to the joint distribution:
vcd::mosaic(~ Sex + Treatment + Improved,
data = Arthritis)
Identifying Improved as the response:
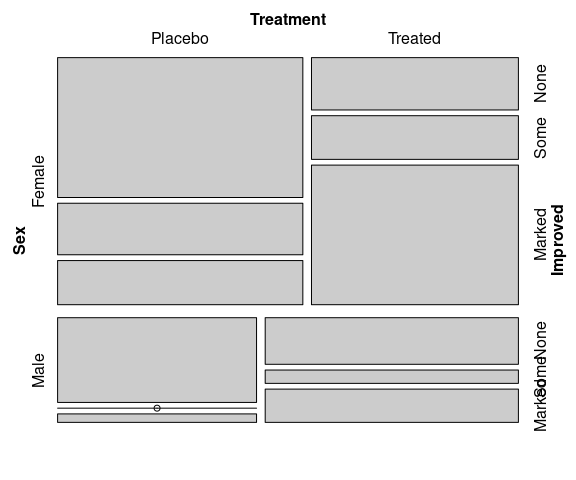
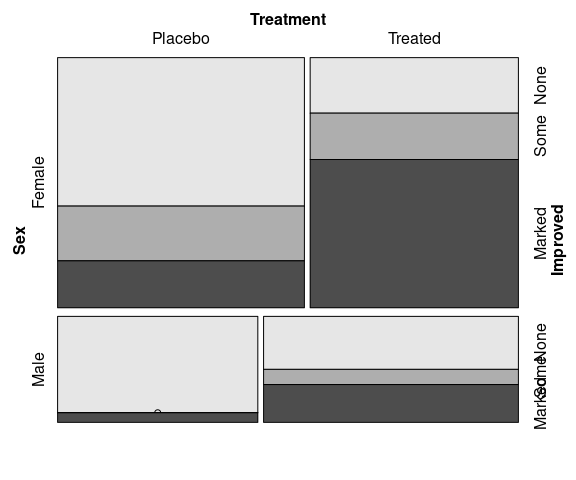
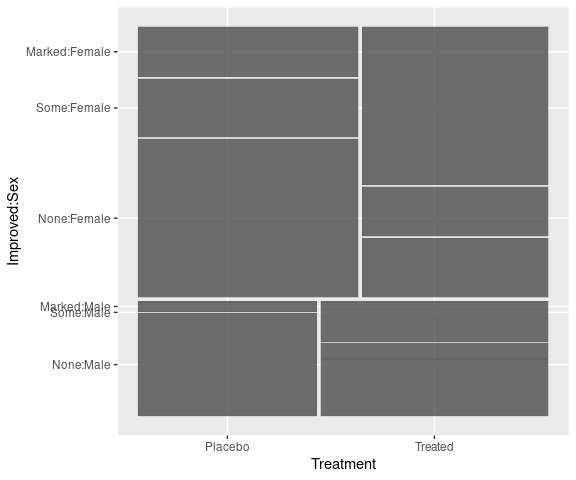
vcd::mosaic(Improved ~ Sex + Treatment,
data = Arthritis)
Matching the doubledecker plots:
vcd::mosaic(
Improved ~ Treatment + Sex,
data = Arthritis,
split_vertical = c(TRUE, TRUE, FALSE))
vcd::mosaic(
Improved ~ Sex + Treatment,
data = Arthritis,
split_vertical = c(TRUE, TRUE, FALSE))
Some variants using ggmosaic:
ggplot(mutate(Arthritis, Sex = fct_rev(Sex))) +
geom_mosaic(
aes(x = product(Treatment,
Sex))) +
coord_flip() +
labs(x = "", y = "")
ggplot(mutate(Arthritis,
Sex = fct_rev(Sex),
Improved = fct_rev(Improved))) +
geom_mosaic(aes(x = product(Improved,
Treatment,
Sex))) +
coord_flip()
A mosaic plot for all bivariate marginals:
pairs(xtabs(~ Sex + Treatment + Improved, data = Arthritis))
Spinograms and CD Plots
Spinograms and CD plots show the conditional distribution of a categorical variable given the value of a numeric variable.
A spinogram for Improved against Age:
ArthT <- filter(Arthritis,
Treatment == "Treated") |>
mutate(Improved = fct_rev(Improved))
arthT_gp <-
grid::gpar(fill = rev(arth_gp$fill))
vcd::spine(Improved ~ Age,
data = ArthT,
gp = arthT_gp,
breaks = 5)
An analogous plot created with ggmosaic by binning the Age variable:
Arth <-
mutate(Arthritis,
AgeBin = cut(Arthritis$Age,
seq(20, by = 10,
len = 7)),
Improved = fct_rev(Improved))
filter(Arth, Treatment == "Treated") |>
count(Improved, AgeBin) |>
ggplot() +
geom_mosaic(aes(weight = n,
x = product(AgeBin),
fill = Improved)) +
scale_fill_brewer(palette = "Blues",
direction = -1,
guide = guide_legend(reverse = TRUE)) +
theme_minimal() +
theme(axis.title = element_blank())
A facet grid can be used to create spinograms for each of the Sex/Treatment combinations:
ggplot(count(Arth, Improved, Sex, Treatment, AgeBin)) +
geom_mosaic(aes(weight = n,
x = product(AgeBin),
fill = Improved)) +
scale_fill_brewer(palette = "Blues",
direction = -1,
guide = guide_legend(reverse = TRUE)) +
theme_minimal() +
facet_grid(Treatment ~ Sex) +
theme(axis.title = element_blank()) +
theme(axis.text.x = element_text(angle = 35,
hjust = 1),
axis.text.y = element_blank())
A spinogram in the media (NYT, August 2021):
Some plots in a Twitter thread :
CD plots estimate the conditional density of the x variable given the levels of y, weighted by the marginal proportions of y and use these to estimate cumulative probabilities.
The slice at a particular x level visualizes the conditional distribution of y given x at that level.
geom_density with position = stack is one way to create a CD plot.
The cd_plot function from the vcd package produces a CD plot using grid graphics.
The cdplot function from the base graphics package provides the same plots using base graphics.
CD plots for the Treated group:
filter(Arthritis, Treatment == "Treated") |>
ggplot(aes(x = Age, fill = Improved)) +
geom_density(position = "fill", bw = 5) +
scale_fill_brewer(palette = "Blues") +
facet_wrap(~ Sex, ncol = 1) +
thm
CD plots for all combinations end up with one group of size one and one of size zero, which produces a non-useful plot for one combination:
count(Arthritis, Treatment, Sex, Improved) |>
complete(Treatment, Sex, Improved,
fill = list(n = 0)) |>
filter(n < 2)
## # A tibble: 2 × 4
## Treatment Sex Improved n
## <fct> <fct> <ord> <int>
## 1 Placebo Male Some 0
## 2 Placebo Male Marked 1
ggplot(Arthritis,
aes(x = Age, fill = Improved)) +
geom_density(position = "fill", bw = 5) +
scale_fill_brewer(palette = "Blues") +
facet_grid(Treatment ~ Sex) +
thm
## Warning: Groups with fewer than two data points have been dropped.
## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning
## -Inf
Uncertainty Representation
Categorical data are often analyzed by fitting models representing conditional independence structures.
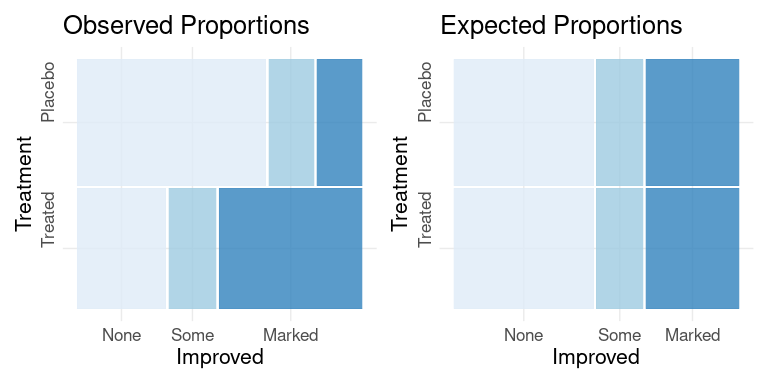
For the Arthritis data, observed counts and expected counts under an independence model assuming Treatment and Improved are independent can be visualized as mosaic plots:
## there are easier ways do do this ...
v <- count(Arthritis, Treatment, Improved)
pT <- group_by(v, Treatment) |>
summarize(n = sum(n)) |>
mutate(pT = n / sum(n)) |>
select(-n)
pI <- group_by(v, Improved) |>
summarize(n = sum(n)) |>
mutate(pI = n / sum(n)) |>
select(-n)
v <- left_join(v, pT, "Treatment") |>
left_join(pI, "Improved") |>
mutate(p = pT * pI,
Treatment = fct_rev(Treatment))
po <- ggplot(v) +
geom_mosaic(aes(weight = n, x = product(Improved, Treatment),
fill = Improved)) +
scale_fill_brewer(palette = "Blues") +
guides(fill = "none") +
labs(title = "Observed Proportions") +
thm +
coord_flip() +
theme(axis.text.y = element_text(angle = 90, hjust = 0))
pe <- ggplot(v) +
geom_mosaic(aes(weight = p, x = product(Improved, Treatment),
fill = Improved)) +
scale_fill_brewer(palette = "Blues") +
guides(fill = "none") +
labs(title = "Expected Proportions") +
thm +
coord_flip() +
theme(axis.text.y = element_text(angle = 90, hjust = 0))
po + pe
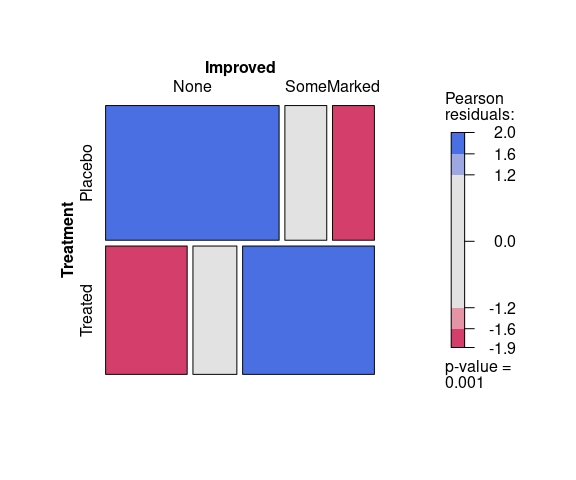
A plot for assessing the fit of the residuals between the observed and expected data under a model assuming independence of Treatment and Improved produces:
vcd::mosaic(~ Treatment + Improved,
data = Arthritis,
gp = vcd::shading_max)
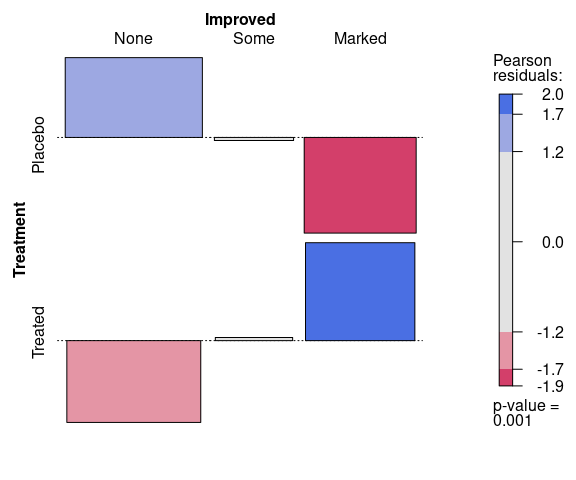
Another visualization of the residuals is the association plot produced by assoc:
vcd::assoc(~ Treatment + Improved,
data = Arthritis,
gp = vcd::shading_max)
Some Other Visualizations
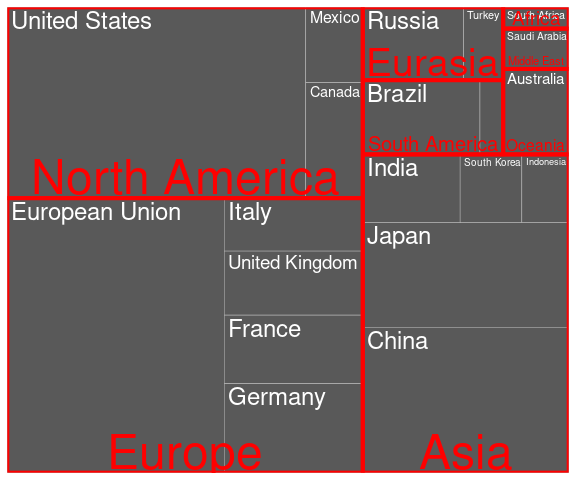
Tree Maps
Tree maps show hierarchically structured (or tree-tructured) data.
Each branch is represented by a rectangle.
Leaf node tiles have areas proportional to the value of a variable.
Tiles are often colored to reflect the value of another variable.
The package treemapify provides a ggplot-based implementation.
The data set G20 includes some variables on the G-20 member countries:
library(treemapify)
select(G20, region,
country, gdp_mil_usd, hdi) |>
knitr::kable(format = "html") |>
kableExtra::kable_styling(
full_width = FALSE)
region
country
gdp_mil_usd
hdi
Africa
South Africa
384315
0.629
North America
United States
15684750
0.937
North America
Canada
1819081
0.911
North America
Mexico
1177116
0.775
South America
Brazil
2395968
0.730
South America
Argentina
474954
0.811
Asia
China
8227037
0.699
Asia
Japan
5963969
0.912
Asia
South Korea
1155872
0.909
Asia
India
1824832
0.554
Asia
Indonesia
878198
0.629
Eurasia
Russia
2021960
0.788
Eurasia
Turkey
794468
0.722
Europe
European Union
16414483
0.876
Europe
Germany
3400579
0.920
Europe
France
2608699
0.893
Europe
United Kingdom
2440505
0.875
Europe
Italy
2014079
0.881
Middle East
Saudi Arabia
727307
0.782
Oceania
Australia
1541797
0.938
A simple tree with only one level, the individual countries:
A corresponding tree map based on gdp_mil_usd:
ggplot(G20, aes(area = gdp_mil_usd)) +
geom_treemap() +
geom_treemap_text(aes(label = country),
color = "white")
A tree grouping by region:
A corresponding tree map:
ggplot(G20, aes(area = gdp_mil_usd,
subgroup = region)) +
geom_treemap() +
geom_treemap_text(aes(label = country),
color = "white") +
geom_treemap_subgroup_border(
color = "red") +
geom_treemap_subgroup_text(color = "red")
A tree map showing GDP values for the G-20 members, grouped by region, with fill mapped to the country’s Human Development Index:
ggplot(G20, aes(area = gdp_mil_usd,
fill = hdi,
subgroup = region)) +
geom_treemap() +
geom_treemap_text(aes(label = country),
color = "white") +
geom_treemap_subgroup_border() +
geom_treemap_subgroup_text(
color = "lightgrey")
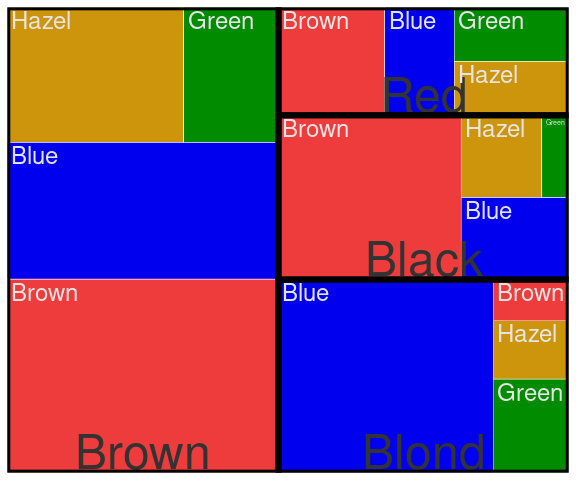
A treemap representing the distribution of eye color within hair color:
group_by(agg, Eye, Hair) |>
summarize(n = sum(n)) |>
ungroup() |>
ggplot(aes(area = n,
subgroup = Hair)) +
geom_treemap(aes(fill = Eye),
color = "white") +
geom_treemap_subgroup_text() +
geom_treemap_subgroup_border(
color = "black", size = 6) +
geom_treemap_text(aes(label = Eye),
color = "grey90") +
scale_fill_manual(values = ecols) +
guides(fill = "none")
A treemap representing proportions for Improved within Treatment within Sex for the Arthritis data:
count(Arth, Treatment, Improved, Sex) |>
ggplot(aes(area = n,
subgroup = Sex, fill = Improved,
subgroup2 = Treatment)) +
geom_treemap() +
geom_treemap_subgroup_text() +
scale_fill_brewer(palette = "Blues",
direction = -1) +
geom_treemap_subgroup_border() +
geom_treemap_subgroup2_text(place = "top",
size = 20)
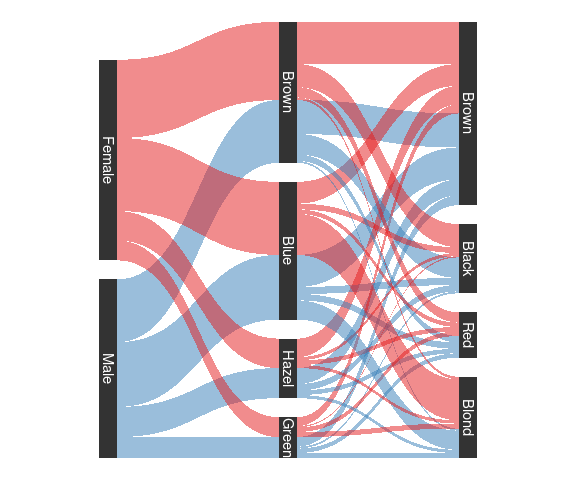
Alluvial plots
These are also known as
parallel sets , or
Sankey diagrams .
They can be viewed as a parallel coordinates plot for categorical data.
Several implementations are available, including:
geom_parallel_sets from ggforce;
geom_sankey from ggsankey
geom_alluvium from ggalluvial.
Hair/Eye color using the ggforce package:
pal <- RColorBrewer::brewer.pal(3, "Set1")
HDF <- mutate(HairEyeColorDF,
Sex = fct_rev(Sex))
library(ggforce)
sHDF <- gather_set_data(HDF, 3 : 1)
sHDF <- mutate(sHDF, x = fct_inorder(as.factor(x))) #**** simplify this?
ggplot(sHDF, aes(x, id = id,
split = y,
value = Freq)) +
geom_parallel_sets(aes(fill = Sex),
alpha = 0.5,
axis.width = 0.1) +
geom_parallel_sets_axes(
axis.width = 0.1) +
geom_parallel_sets_labels(
colour = 'white') +
scale_fill_manual(
values = c(Male = pal[2],
Female = pal[1])) +
theme_void() + guides(fill = "none")
Arthritis data with ggforce:
sArth <- mutate(Arth,
Improved = factor(Improved,
ordered = FALSE)) |>
count(Improved, Treatment, Sex) |>
gather_set_data(3 : 1)
sArth <- mutate(sArth,
x = fct_inorder(factor(x)),
Sex = fct_rev(Sex))
ggplot(sArth, aes(x,
id = id,
split = y,
value = n)) +
geom_parallel_sets(aes(fill = Sex),
alpha = 0.5,
axis.width = 0.1) +
geom_parallel_sets_axes(axis.width = 0.1) +
geom_parallel_sets_labels(
colour = 'white') +
scale_fill_manual(
values = c(Male = pal[2],
Female = pal[1])) +
theme_void() + guides(fill = "none")
Stream Graphs
Stream graphs are a generalization of stacked bar charts plotted against a numeric variable.
In some cases the origins of the bars are shifted to improve some aspect of the overall visualization.
An early example is the Baby Name Voyager . (A more recent variant is also available .)
A NY Times visualization of movie box office results is another example. (Blog post with a static version ).
Some R implementations on GitHub:
A stream graph for movie genres (these are not mutually exclusive):
## install with: remotes::install_github("hrbrmstr/streamgraph")
library(streamgraph)
library(tidyverse)
genres <- c("Action", "Animation", "Comedy",
"Drama", "Documentary", "Romance")
mymovies <- select(ggplot2movies::movies,
year, one_of(genres))
mymovies_long <- pivot_longer(
mymovies, -year,
names_to = "genre",
values_to = "value")
movie_counts <- count(mymovies_long,
year, genre)
streamgraph(movie_counts, "genre", "n", "year")
Interactive Tutorial
An interactive learnravailable .
You can run the tutorial with
STAT4580::runTutorial("proportions")You can install the current version of the STAT4580 package with
remotes::install_gitlab("luke-tierney/STAT4580")You may need to install the remotes package from CRAN first.
Exercises
Figure A shows a bar char of the flights leaving NYC airports in 2013 for each day of the week. Figure B shows the market share of five major internet browsers in 2015.
For which of these bar charts would it be better to reorder the categories so the bars are ordered from largest to smallest?
Yes for Figure A. No for Figure B.
No for Figure A. Yes for Figure B.
Yes for both.
No for both.
Consider the stacked bar chart p1 and the spine plot p2 for the hair and eye color data produced by the following code:
library(dplyr)
library(ggplot2)
library(ggmosaic)
ecols <- c(Brown = "brown4", Blue = "blue2",
Hazel = "darkgoldenrod3", Green = "green4")
HairEyeColorDF <- as.data.frame(HairEyeColor)
p0 <- ggplot(HairEyeColorDF) +
scale_fill_manual(values = ecols) +
theme_minimal()
p1 <- p0 + geom_col(aes(x = Hair, y = Freq / sum(Freq), fill = Eye))
p2 <- p0 + geom_mosaic(aes(x = product(Hair), fill = Eye, weight = Freq))Use the two plots to answer: Which hair color has the highest proportion of individuals with green eyes?
Black
Brown
Red
Blond
Which plot makes it easiest to answer this question?
Use the plots of the previous question to answer: The proportion of individuals with red hair is closest to:
5%
8%
12%
20%
Which plot makes it easiest to answer this question?
LS0tCnRpdGxlOiAiVmlzdWFsaXppbmcgUHJvcG9ydGlvbnMiCm91dHB1dDoKICBodG1sX2RvY3VtZW50OgogICAgdG9jOiB5ZXMKICAgIGNvZGVfZm9sZGluZzogc2hvdwogICAgY29kZV9kb3dubG9hZDogdHJ1ZQotLS0KCjxsaW5rIHJlbD0ic3R5bGVzaGVldCIgaHJlZj0ic3RhdDQ1ODAuY3NzIiB0eXBlPSJ0ZXh0L2NzcyIgLz4KPHN0eWxlIHR5cGU9InRleHQvY3NzIj4gLnJlbWFyay1jb2RlIHsgZm9udC1zaXplOiA4NSU7IH0gPC9zdHlsZT4KPCEtLSB0aXRsZSBiYXNlZCBvbiBXaWxrZSdzIGNoYXB0ZXIgLS0+CgpgYGB7ciBzZXR1cCwgaW5jbHVkZSA9IEZBTFNFLCBtZXNzYWdlID0gRkFMU0V9CnNvdXJjZShoZXJlOjpoZXJlKCJzZXR1cC5SIikpCmtuaXRyOjpvcHRzX2NodW5rJHNldChjb2xsYXBzZSA9IFRSVUUsIG1lc3NhZ2UgPSBGQUxTRSwKICAgICAgICAgICAgICAgICAgICAgIGZpZy5oZWlnaHQgPSA1LCBmaWcud2lkdGggPSA2LCBmaWcuYWxpZ24gPSAiY2VudGVyIikKCnNldC5zZWVkKDEyMzQ1KQpsaWJyYXJ5KGRwbHlyKQpsaWJyYXJ5KGdncGxvdDIpCmxpYnJhcnkobGF0dGljZSkKbGlicmFyeShncmlkRXh0cmEpCmxpYnJhcnkocGF0Y2h3b3JrKQpzb3VyY2UoaGVyZTo6aGVyZSgiZGF0YXNldHMuUiIpKQpgYGAKCgojIyBDYXRlZ29yaWNhbCBEYXRhCgpDYXRlZ29yaWNhbCBkYXRhIGNhbiBiZQoKKiBub21pbmFsLCBxdWFsaXRhdGl2ZQoKKiBvcmRpbmFsCgpGb3IgdmlzdWFsaXphdGlvbiwgdGhlIG1haW4gZGlmZmVyZW5jZSBpcyB0aGF0IG9yZGluYWwgZGF0YSBzdWdnZXN0cyBhCnBhcnRpY3VsYXIgZGlzcGxheSBvcmRlci4KClB1cmVseSBjYXRlZ29yaWNhbCBkYXRhIGNhbiBjb21lIGluIGEgcmFuZ2Ugb2YgZm9ybWF0cy4KClRoZSBtb3N0IGNvbW1vbiBhcmUKCiogcmF3IGRhdGE6IGluZGl2aWR1YWwgb2JzZXJ2YXRpb25zOwoKKiBhZ2dyZWdhdGVkIGRhdGE6IGNvdW50cyBmb3IgZWFjaCB1bmlxdWUgY29tYmluYXRpb24gb2YgbGV2ZWxzOwoKKiBjcm9zcy10YWJ1bGF0ZWQgZGF0YS4KCgojIyMgUmF3IERhdGEKCmBgYHtyLCBlY2hvID0gRkFMU0V9CmFoIDwtIGFzLmRhdGEuZnJhbWUoSGFpckV5ZUNvbG9yKQpyYXcgPC0gYWhbcmVwKHNlcV9sZW4obnJvdyhhaCkpLCB0aW1lcyA9IGFoJEZyZXEpLCBdWy00XQpyYXcgPC0gcmF3W3NhbXBsZShzZXFfbGVuKG5yb3cocmF3KSkpLCBdCnJvdy5uYW1lcyhyYXcpIDwtIE5VTEwKYGBgCgpSYXcgZGF0YSBmb3IgYSBzdXJ2ZXkgb2YgaW5kaXZpZHVhbHMgdGhhdCByZWNvcmRzIGhhaXIgY29sb3IsIGV5ZQpjb2xvciwgYW5kIGdlbmRlciBvZiBgciBucm93KHJhdylgIGluZGl2aWR1YWxzIG1pZ2h0IGxvb2sgbGlrZSB0aGlzOgoKYGBge3J9CmhlYWQocmF3KQpgYGAKCgojIyMgQWdncmVnYXRlZCBEYXRhCgpPbmUgd2F5IHRvIGFnZ3JlZ2F0ZSByYXcgY2F0ZWdvcmljYWwgZGF0YSBpcyB0byB1c2UgYGNvdW50YCBmcm9tIGBkcGx5cmA6CgpgYGB7cn0KbGlicmFyeShkcGx5cikKYWdnIDwtIGNvdW50KHJhdywgSGFpciwgRXllLCBTZXgpIHw+CiAgICBhc190aWJibGUoKQphZ2cKYGBgCgo8IS0tClRoZSBgY291bnRfYCBmdW5jdGlvbiBmcm9tIGBkcGx5cmAgYWxsb3dzIHRoZSB2YXJpYWJsZXMgdG8gdXNlIHRvIGJlCnJlYWQgZnJvbSB0aGUgZGF0YToKCmBgYHtyLCBldmFsID0gRkFMU0V9CmFnZyA8LSBjb3VudF8ocmF3LCBuYW1lcyhyYXcpKQpoZWFkKGFnZykKYGBgCgpBcHBhcmVudGx5IHRoZSAibW9kZXJuIiB3YXkgdG8gZG8gdGhpcyBpcwoKYGBge3J9CmNvdW50KHJhdywgISEhIHN5bXMobmFtZXMocmF3KSkpCmBgYAotLT4KCgojIyMgQ3Jvc3MtVGFidWxhdGVkIERhdGEKCkNyb3NzLXRhYnVsYXRlZCBkYXRhIGNhbiBiZSBwcm9kdWNlZCBmcm9tIGFnZ3JlZ2F0ZSBkYXRhIHVzaW5nIGB4dGFic2A6CgpgYGB7cn0KeHRhYnMobiB+IEhhaXIgKyBFeWUgKyBTZXgsIGRhdGEgPSBhZ2cpCmBgYAoKQ3Jvc3MtdGFidWxhdGVkIGRhdGEgY2FuIGJlIHByb2R1Y2VkIGZyb20gcmF3IGRhdGEgdXNpbmcgYHRhYmxlYDoKCmBgYHtyfQp4dGIgPC0gdGFibGUocmF3KQp4dGIKYGBgCgpCb3RoIHJhdyBhbmQgYWdncmVnYXRlIGRhdGEgaW4gdGhpcyBleGFtcGxlIGFyZSBpbiBfdGlkeV8gZm9ybTsgdGhlCmNyb3NzLXRhYnVsYXRlZCBkYXRhIGlzIG5vdC4KCkNyb3NzLXRhYnVsYXRlZCBkYXRhIG9uICRwJCB2YXJpYWJsZXMgaXMgYXJyYW5nZWQgaW4gYSAkcCQtd2F5IGFycmF5LgoKVGhlIGNyb3NzLXRhYnVsYXRlZCBkYXRhIGNhbiBiZSBjb252ZXJ0ZWQgdG8gdGhlIHRpZHkgYWdncmVnYXRlIGZvcm0KdXNpbmcgYGFzLmRhdGEuZnJhbWVgOgoKYGBge3J9CmNsYXNzKHh0YikKaGVhZChhcy5kYXRhLmZyYW1lKHh0YikpCmBgYAoKVGhlIHZhcmlhYmxlIGB4dGJgIGNvcnJlc3BvbmRzIHRvIHRoZSBkYXRhIHNldCBgSGFpckV5ZUNvbG9yYCBpbiB0aGUKYGRhdGFzZXRzYCBwYWNrYWdlLAoKCiMjIyBXb3JraW5nIFdpdGggQ2F0ZWdvcmljYWwgVmFyaWFibGVzCgpDYXRlZ29yaWNhbCB2YXJpYWJsZXMgYXJlIHVzdWFsbHkgcmVwcmVzZW50ZWQgYXM6CgoqIGNoYXJhY3RlciB2ZWN0b3JzCgoqIGZhY3RvcnMuCgpTb21lIGFkdmFudGFnZXMgb2YgZmFjdG9yczoKCiogbW9yZSBjb250cm9sIG92ZXIgb3JkZXJpbmcgb2YgbGV2ZWxzCgoqIGxldmVscyBhcmUgcHJlc2VydmVkIHdoZW4gZm9ybWluZyBzdWJzZXRzCgoqIGxldmVscyBjYW4gcmVmbGVjdCBwb3NzaWJsZSB2YWx1ZXMgbm90IHByZXNlbnQgaW4gdGhlIGRhdGEKCk1vc3QgcGxvdHRpbmcgYW5kIG1vZGVsaW5nIGZ1bmN0aW9ucyB3aWxsIGNvbnZlcnQgY2hhcmFjdGVyIHZlY3RvcnMgdG8KZmFjdG9ycyB3aXRoIGxldmVscyBvcmRlcmVkIGFscGhhYmV0aWNhbGx5LgoKU29tZSBzdGFuZGFyZCBSIGZ1bmN0aW9ucyBmb3Igd29ya2luZyB3aXRoIGZhY3RvcnMgaW5jbHVkZQoKKiBgZmFjdG9yYCBjcmVhdGVzIGEgZmFjdG9yIGZyb20gYW5vdGhlciB0eXBlIG9mIHZhcmlhYmxlCiogYGxldmVsc2AgcmV0dXJucyB0aGUgbGV2ZWxzIG9mIGEgZmFjdG9yCiogYHJlb3JkZXJgIGNoYW5nZXMgbGV2ZWwgb3JkZXIgdG8gbWF0Y2ggYW5vdGhlciB2YXJpYWJsZQoqIGByZWxldmVsYCBtb3ZlcyBhIHBhcnRpY3VsYXIgbGV2ZWwgdG8gdGhlIGZpcnN0IHBvc2l0aW9uIGFzIGEgYmFzZSBsaW5lCiogYGRyb3BsZXZlbHNgIHJlbW92ZXMgbGV2ZWxzIG5vdCBpbiB0aGUgdmFyaWFibGUuCgpUaGUgYHRpZHl2ZXJzZWAgcGFja2FnZSBgZm9yY2F0c2AgYWRkcyBzb21lIG1vcmUgdG9vbHMsIGluY2x1ZGluZwoKKiBgZmN0X2lub3JkZXJgIGNyZWF0ZXMgYSBmYWN0b3Igd2l0aCBsZXZlbHMgb3JkZXJlZCBieSBmaXJzdCBhcHBlYXJhbmNlCiogYGZjdF9pbmZyZXFgIG9yZGVycyBsZXZlbHMgYnkgZGVjcmVhc2luZyBmcmVxdWVuY3kKKiBgZmN0X3JldmAgcmV2ZXJzZXMgdGhlIGxldmVscwoqIGBmY3RfcmVjb2RlYCBjaGFuZ2VzIGZhY3RvciBsZXZlbHMKKiBgZmN0X3JlbGV2ZWxgIG1vdmVzIG9uZSBvciBtb3JlIGxldmVscwoqIGBmY3RfY2AgbWVyZ2VzIHR3byBvciBtb3JlIGZhY3RvcnMKKiBgZmN0X2NvbGxhcHNlYCBtZXJnZSBzb21lIGZhY3RvciBsZXZlbHMKCgojIyBCYXIgQ2hhcnRzIEZvciBGcmVxdWVuY2llcwoKCiMjIyBCYXNpY3MKCkEgYmFyIGNoYXJ0IGlzIG9mdGVuIHVzZWQgdG8gc2hvdyB0aGUgZnJlcXVlbmNpZXMgb2YgYSBjYXRlZ29yaWNhbAp2YXJpYWJsZS4KCkJ5IGRlZmF1bHQsIGBnZW9tX2JhcmAgdXNlcyBgc3RhdCA9ICJjb3VudCJgIGFuZCBtYXBzIGl0cyByZXN1bHQgdG8KdGhlIGB5YCBhZXN0aGV0aWMuCgpUaGlzIGlzIHN1aXRhYmxlIGZvciByYXcgZGF0YToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KdGhtIDwtIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZSh0ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSAxNikpCmdncGxvdChyYXcpICsKICAgIGdlb21fYmFyKGFlcyh4ID0gSGFpciksCiAgICAgICAgICAgICBmaWxsID0gImRlZXBza3libHVlMyIpICsKICAgIHRobQpgYGAKCkZvciBhIG5vbWluYWwgdmFyaWFibGUgaXQgaXMgb2Z0ZW4gYmV0dGVyIHRvIG9yZGVyIHRoZSBiYXJzIGJ5CmRlY3JlYXNpbmcgZnJlcXVlbmN5OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpsaWJyYXJ5KGZvcmNhdHMpCmdncGxvdChtdXRhdGUocmF3LAogICAgICAgICAgICAgIEhhaXIgPSBmY3RfaW5mcmVxKEhhaXIpKSkgKwogICAgZ2VvbV9iYXIoYWVzKHggPSBIYWlyKSwKICAgICAgICAgICAgIGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgdGhtCmBgYAoKSWYgdGhlIGRhdGEgaGF2ZSBhbHJlYWR5IGJlZW4gYWdncmVnYXRlZCwgdGhlbiB5b3UgbmVlZCB0byBlaXRoZXIKCiogc3BlY2lmeSBgc3RhdCA9ICJpZGVudGl0eSJgIGFzIHdlbGwgYXMgdGhlIHZhcmlhYmxlIGNvbnRhaW5pbmcgdGhlCiAgY291bnRzIGFzIHRoZSBgeWAgYWVzdGhldGljLCBvcgoKKiB1c2UgYGdlb21fY29sYDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGFnZykgKwogICAgZ2VvbV9jb2woYWVzKHggPSBIYWlyLAogICAgICAgICAgICAgICAgIHkgPSBuKSwKICAgICAgICAgICAgIGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgdGhtCmBgYAoKRm9yIGFnZ3JlZ2F0ZWQgZGF0YSwgcmVvcmRlcmluZyBjYW4gYmUgYmFzZWQgb24gdGhlIGNvbXB1dGVkIGNvdW50cwp1c2luZwoKYGBge3J9CmFnZ19vcmQgPC0KICAgIG11dGF0ZShhZ2csCiAgICAgICAgICAgSGFpciA9IHJlb3JkZXIoSGFpciwgLW4sIHN1bSkpCmBgYAoKKiBgLW5gIGlzIHVzZWQgdG8gb3JkZXIgbGFyZ2VzdCB0byBzbWFsbGVzdDsKCiogdGhlIGRlZmF1bHQgc3VtbWFyeSB1c2VkIGJ5IGByZW9yZGVyYCBpcyBgbWVhbmA7IGBzdW1gIGlzIGJldHRlciBoZXJlLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoYWdnX29yZCkgKwogICAgZ2VvbV9jb2woYWVzKHggPSBIYWlyLAogICAgICAgICAgICAgICAgIHkgPSBuKSwKICAgICAgICAgICAgIGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgdGhtCmBgYAoKCiMjIyBBZGRpbmcgYSBHcm91cGluZyBWYXJpYWJsZQoKTWFwcGluZyB0aGUgYEV5ZWAgdmFyaWFibGUgdG8gYGZpbGxgIGluIGBnZ3Bsb3RgIHByb2R1Y2VzIGEgX3N0YWNrZWQKYmFyIGNoYXJ0Xy4KCkFuIGFsdGVybmF0aXZlLCBzcGVjaWZpZWQgd2l0aCBgcG9zaXRpb24gPSAiZG9kZ2UiYCwgaXMgYSBfc2lkZSBieQpzaWRlXyBiYXIgY2hhcnQsIG9yIGEgX2NsdXN0ZXJlZF8gYmFyIGNoYXJ0LgoKRm9yIHRoZSBzaWRlIGJ5IHNpZGUgY2hhcnQgaW4gcGFydGljdWxhciBpdCBtYXkgYmUgdXNlZnVsIHRvIGFsc28KcmVvcmRlciB0aGUgYEV5ZWAgY29sb3IgbGV2ZWxzLgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQplY29scyA8LSBjKEJyb3duID0gImJyb3duNCIsCiAgICAgICAgICAgQmx1ZSA9ICJibHVlMiIsCiAgICAgICAgICAgSGF6ZWwgPSAiZGFya2dvbGRlbnJvZDMiLAogICAgICAgICAgIEdyZWVuID0gImdyZWVuNCIpCmFnZ19vcmQgPC0KICAgIG11dGF0ZShhZ2csCiAgICAgICAgICAgSGFpciA9IHJlb3JkZXIoSGFpciwgLW4sIHN1bSksCiAgICAgICAgICAgRXllID0gcmVvcmRlcihFeWUsIC1uLCBzdW0pKQpwMSA8LSBnZ3Bsb3QoYWdnX29yZCkgKwogICAgZ2VvbV9jb2woYWVzKHggPSBIYWlyLAogICAgICAgICAgICAgICAgIHkgPSBuLAogICAgICAgICAgICAgICAgIGZpbGwgPSBFeWUpKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBlY29scykgKwogICAgdGhtCnAyIDwtIGdncGxvdChhZ2dfb3JkKSArCiAgICBnZW9tX2NvbChhZXMoeCA9IEhhaXIsCiAgICAgICAgICAgICAgICAgeSA9IG4sCiAgICAgICAgICAgICAgICAgZmlsbCA9IEV5ZSksCiAgICAgICAgICAgICBwb3NpdGlvbiA9ICJkb2RnZSIpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGVjb2xzKSArCiAgICB0aG0KKHAxICsgZ3VpZGVzKGZpbGwgPSAibm9uZSIpKSB8IHAyCmBgYAoKRmFjZXRpbmcgY2FuIGJlIHVzZWQgdG8gYnJpbmcgaW4gYWRkaXRpb25hbCB2YXJpYWJsZXM6CgpgYGB7ciwgZmlnLndpZHRoID0gOCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAxICsgZmFjZXRfd3JhcCh+IFNleCkKYGBgCgpUaGUgY291bnRzIHNob3duIGhlcmUgbWF5IG5vdCBiZSB0aGUgbW9zdCByZWxldmFudCBmZWF0dXJlcyBmb3IKdW5kZXJzdGFuZGluZyB0aGUgam9pbnQgZGlzdHJpYnV0aW9ucyBvZiB0aGVzZSB2YXJpYWJsZXMuCgoKIyMgUGllIENoYXJ0cyBhbmQgRG91Z2hudXQgQ2hhcnRzCgpfUGllIGNoYXJ0c18gZ28gYnkgbWFueSBkaWZmZXJlbnQgbmFtZXMgKGZyb20gYSBbVHdpdHRlcgp0aHJlYWRdKGh0dHBzOi8vdHdpdHRlci5jb20vRWxlcGhhbnRFYXRpbmcvc3RhdHVzLzEzNjEwMzk3NzE0MTQzMTkxMDYpKToKCmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI4MCUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoInBpZW5hbWVzLmpwZWciKSkKYGBgCgpQaWUgY2hhcnRzIGNhbiBiZSB2aWV3ZWQgYXMgc3RhY2tlZCBiYXIgY2hhcnRzIGluIHBvbGFyIGNvb3JkaW5hdGVzOgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpoY29scyA8LSBjKEJsYWNrID0gImJsYWNrIiwgQnJvd24gPSAiYnJvd240IiwKICAgICAgICAgICBSZWQgPSAiYnJvd24xIiwgQmxvbmQgPSAibGlnaHRnb2xkZW5yb2QxIikKcDEgPC0gZ2dwbG90KGFnZ19vcmQpICsKICAgIGdlb21fY29sKGFlcyh4ID0gMSwgeSA9IG4sIGZpbGwgPSBIYWlyKSwgcG9zaXRpb24gPSAiZmlsbCIpICsKICAgIGNvb3JkX3BvbGFyKHRoZXRhID0gInkiKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBoY29scykgKwogICAgdGhtCnAyIDwtIGdncGxvdChhZ2dfb3JkKSArCiAgICBnZW9tX2NvbChhZXMoeCA9IEhhaXIsIHkgPSBuLCBmaWxsID0gSGFpcikpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGhjb2xzKSArCiAgICB0aG0KKHAxICsgZ3VpZGVzKGZpbGwgPSAibm9uZSIpKSB8IHAyCmBgYAoKVGhlIGF4ZXMgYW5kIGdyaWQgbGluZXMgYXJlIG5vdCBoZWxwZnVsIGZvciB0aGUgcGllIGNoYXJ0IGFuZCBjYW4gYmUKcmVtb3ZlZCB3aXRoIHNvbWUgX3RoZW1lXyBzZXR0aW5ncy4KClVzaW5nIGZhY2V0aW5nIHdlIGNhbiBhbHNvIHNlcGFyYXRlbHkgc2hvdyB0aGUgZGlzdHJpYnV0aW9ucyBmb3IgbWVuCmFuZCB3b21lbjoKCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcGllX3RobSA8LSB0aG0gKwogICAgdGhlbWUoYXhpcy50aXRsZSA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGV4dCA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGlja3MgPSBlbGVtZW50X2JsYW5rKCksCiAgICAgICAgICBwYW5lbC5ncmlkLm1ham9yID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgcGFuZWwuZ3JpZC5taW5vciA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIHBhbmVsLmJvcmRlciA9IGVsZW1lbnRfYmxhbmsoKSkKCnAzIDwtIHAxICsgZmFjZXRfd3JhcCh+IFNleCkgKyBwaWVfdGhtCnAzCmBgYAoKX0RvdWdobnV0IGNoYXJ0c18gYXJlIGEgdmFyaWFudCB0aGF0IGhhcyByZWNlbnRseSBiZWNvbWUgcG9wdWxhciBpbgp0aGUgbWVkaWE6CgpgYGB7ciwgZmlnLndpZHRoID0gOCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnA0IDwtIHAzICsgeGxpbSgwLCAxLjUpCnA0CmBgYAoKVGhlIGNlbnRlciBpcyBvZnRlbiB1c2VkIGZvciBhbm5vdGF0aW9uOgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwNCArIGdlb21fdGV4dChhZXMoeCA9IDAsIHkgPSAwLCBsYWJlbCA9IFNleCksIHNpemUgPSA1KSArCiAgICB0aGVtZShzdHJpcC5iYWNrZ3JvdW5kID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgc3RyaXAudGV4dCA9IGVsZW1lbnRfYmxhbmsoKSkKYGBgCgpBbiBhbHRlcm5hdGl2ZSB0byB0aGUgcG9sYXIgY29vcmRpbmF0ZXMgYXBwcm9hY2ggdXNlcwpgZ2VvbV9hcmNfYmFyYCBhbmQgYHN0YXRfcGllYCBmcm9tIHBhY2thZ2UgYGdnZm9yY2VgOgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQojfCB3YXJuaW5nOiBmYWxzZQpsaWJyYXJ5KGdnZm9yY2UpCmFycmFuZ2UoYWdnX29yZCwgZGVzYyhIYWlyKSkgfD4KICAgIGdncGxvdChhZXMoeDAgPSAwLCB5MCA9IDAsIHIwID0gMCwgciA9IDEsIGFtb3VudCA9IG4sIGZpbGwgPSBIYWlyKSkgKwogICAgZ2VvbV9hcmNfYmFyKHN0YXQgPSAicGllIiwgY29sb3IgPSBOQSkgKwogICAgY29vcmRfZml4ZWQoKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBoY29scykgKwogICAgcGllX3RobSArCiAgICBmYWNldF93cmFwKH4gU2V4KQpgYGAKCkZvciBkb3VnaG51dCBjaGFydHM6CgpgYGB7ciwgZmlnLndpZHRoID0gOCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmFycmFuZ2UoYWdnX29yZCwgZGVzYyhIYWlyKSkgfD4KICAgIGdncGxvdChhZXMoeDAgPSAwLCB5MCA9IDAsIHIwID0gMC40LCByID0gMSwgYW1vdW50ID0gbiwgZmlsbCA9IEhhaXIpKSArCiAgICBnZW9tX2FyY19iYXIoc3RhdCA9ICJwaWUiLCBjb2xvciA9IE5BKSArCiAgICBnZW9tX3RleHQoYWVzKHggPSAwLCB5ID0gMCwgbGFiZWwgPSBTZXgpLCBzaXplID0gNSkgKwogICAgY29vcmRfZml4ZWQoKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBoY29scykgKwogICAgcGllX3RobSArCiAgICB0aGVtZShzdHJpcC5iYWNrZ3JvdW5kID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgc3RyaXAudGV4dCA9IGVsZW1lbnRfYmxhbmsoKSkgKwogICAgZmFjZXRfd3JhcCh+IFNleCkKYGBgCgoKIyMgU29tZSBOb3RlcwoKUGllIGNoYXJ0cyBhcmUgZWZmZWN0aXZlIGZvciBqdWRnaW5nIHBhcnQvd2hvbGUgcmVsYXRpb25zaGlwcy4KClBpZSBjaGFydHMgY2FuIGJlIGVmZmVjdGl2ZSBmb3IgY29tcGFyaW5nIHByb3BvcnRpb25zIHRvCgoqIG9uZSBoYWxmCiogb25lIHF1YXJ0ZXIKClBpZSBjaGFydHMgYXJlIG5vdCB2ZXJ5IGVmZmVjdGl2ZSBmb3IgY29tcGFyaW5nIHByb3BvcnRpb25zIHRvIGVhY2ggb3RoZXIuCgozRCBwaWUgY2hhcnRzIGFyZSBwb3B1bGFyIGFuZCBhIHZlcnkgYmFkIGlkZWEuIEFuIGV4YW1wbGUKKFtGaWcuIDYuNjFdKGh0dHBzOi8vd3d3LmRyb3Bib3guY29tL3MvdGxlaHppM2tiNmlrYnN6LzYuNjEuM0RJbGx1c3RyYXRpb24ucG5nP2RsPTApKQpmcm9tIEFuZHkgS2lyaydzIGJvb2sgKDIwMTYpLApbX0RhdGEgVmlzdWFsaXphdGlvbjogQSBIYW5kYm9vayBmb3IgRGF0YSBEcml2ZW4gRGVzaWduX10oaHR0cDovL2Jvb2sudmlzdWFsaXNpbmdkYXRhLmNvbS9ob21lKToKCmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI1MCUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoImJhZHBpZS5wbmciKSkKYGBgCgpQaWUgY2hhcnRzIGFyZSB3aWRlbHkgdXNlZCBmb3IgcG9saXRpY2FsIGRhdGEuCgoqIFdpdGggdGhlIHJpZ2h0IG9yZGVyaW5nLCBwaWUgY2hhcnRzIGFyZSB2ZXJ5IGdvb2QgYXQgc2hvd2luZwogIHdoaWNoIGNvYWxpdGlvbnMgb2YgcGFydGllcyBjYW4gZm9ybSBhIG1ham9yaXR5LgoKKiBXaGVuIG5vIG9uZSBjYW5kaWRhdGUgZWFybnMgYSBtYWpvcml0eSBvZiB0aGUgdm90ZXMsIHBpZSBjaGFydHMKICBkbyBub3Qgc2hvdyB3aGljaCBjYW5kaWRhdGUgaGFzIGVhcm5lZCBhIHBsdXJhbGl0eSB2ZXJ5IHdlbGwuCgoqIEdvb2Qgb3JpZW50YXRpb24gYW5kIGZhY3RvciBvcmRlcmluZyBjYW4gaGVscC4KCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZWxlY3QgPC0gZ2VvZmFjZXQ6OmVsZWN0aW9uIHw+CiAgICBncm91cF9ieShjYW5kaWRhdGUpIHw+CiAgICBzdW1tYXJpemUodm90ZXMgPSBzdW0odm90ZXMpKQoKcDEgPC0gZ2dwbG90KGVsZWN0KSArCiAgICBnZW9tX2NvbChhZXMoeCA9IDEsIHkgPSB2b3RlcywgZmlsbCA9IGNhbmRpZGF0ZSksIHBvc2l0aW9uID0gImZpbGwiKSArCiAgICBjb29yZF9wb2xhcih0aGV0YSA9ICJ5Iiwgc3RhcnQgPSAtMSkgKwogICAgeGxpbShjKC0wLjUsIDEuNSkpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGMoVHJ1bXAgPSBzY2FsZXM6Om11dGVkKCJyZWQiLCA1MCwgODApLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBDbGludG9uID0gc2NhbGVzOjptdXRlZCgiYmx1ZSIsIDUwLCA3MCksCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIE90aGVyID0gImdyZXkiKSkgKwogICAgcGllX3RobQoKcDIgPC0gbXV0YXRlKGVsZWN0LAogICAgICAgICAgICAgY2FuZGlkYXRlID0gZmFjdG9yKGNhbmRpZGF0ZSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBjKCJDbGludG9uIiwgIk90aGVyIiwgIlRydW1wIikpKSB8PgogICAgZ2dwbG90KCkgKwogICAgZ2VvbV9jb2woYWVzKHggPSAxLCB5ID0gdm90ZXMsIGZpbGwgPSBjYW5kaWRhdGUpLCBwb3NpdGlvbiA9ICJmaWxsIikgKwogICAgY29vcmRfcG9sYXIodGhldGEgPSAieSIpICsKICAgIHhsaW0oYygtMC41LCAxLjUpKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBjKFRydW1wID0gc2NhbGVzOjptdXRlZCgicmVkIiwgNTAsIDgwKSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgQ2xpbnRvbiA9IHNjYWxlczo6bXV0ZWQoImJsdWUiLCA1MCwgNzApLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBPdGhlciA9ICJncmV5IikpICsKICAgIHBpZV90aG0KCnAzIDwtIGdncGxvdChlbGVjdCkgKwogICAgZ2VvbV9jb2woYWVzKHggPSBjYW5kaWRhdGUsCiAgICAgICAgICAgICAgICAgeSA9IDEwMCAqICh2b3RlcyAvIHN1bSh2b3RlcykpLAogICAgICAgICAgICAgICAgIGZpbGwgPSBjYW5kaWRhdGUpKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBjKFRydW1wID0gc2NhbGVzOjptdXRlZCgicmVkIiwgNTAsIDgwKSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgQ2xpbnRvbiA9IHNjYWxlczo6bXV0ZWQoImJsdWUiLCA1MCwgNzApLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBPdGhlciA9ICJncmV5IikpICsKICAgIGxhYnMoeSA9ICJwZXJjZW50IikgKwogICAgdGhtICsKICAgIHRoZW1lKGF4aXMudGV4dC54ID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgYXhpcy50aXRsZS54ID0gZWxlbWVudF9ibGFuaygpKQoKKHAxICsgZ3VpZGVzKGZpbGwgPSAibm9uZSIpKSArIChwMiArIGd1aWRlcyhmaWxsID0gIm5vbmUiKSkgKyBwMwpgYGAKCgojIyBTb21lIEFsdGVybmF0aXZlcwoKCiMjIyBTdGFja2VkIEJhciBDaGFydHMKClN0YWNrZWQgYmFyIGNoYXJ0cyB3aXRoIGVxdWFsIGhlaWdodHMsIG9yIGZpbGxlZCBiYXIgY2hhcnRzLCBhcmUgYW4KYWx0ZXJuYXRpdmUgZm9yIHJlcHJlc2VudGluZyBwYXJ0LXdob2xlIHJlbGF0aW9uc2hpcHMuCgoqIFRvcCBhbmQgYm90dG9tIHByb3BvcnRpb25zIGFyZSBlYXN5IHRvIGNvbXBhcmUuCgoqIENvbXBhcmluZyBwcm9wb3J0aW9ucyB0byBvbmUgaGFsZiBhbmQgb25lIHF1YXJ0ZXIgaXMgaGFyZGVyLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoYWdnKSArCiAgICBnZW9tX2NvbChhZXMoeCA9IFNleCwgeSA9IG4sIGZpbGwgPSBIYWlyKSwgcG9zaXRpb24gPSAiZmlsbCIpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGhjb2xzKSArCiAgICB0aG0KYGBgCgoKIyMjIFdhZmZsZSBDaGFydHMKCkFub3RoZXIgYWx0ZXJuYXRpdmUgaXMgYSBfd2FmZmxlIGNoYXJ0Xywgc29tZXRpbWVzIGFsc28gY2FsbGVkIGEKX3NxdWFyZSBwaWUgY2hhcnRfLgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjUwJSJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygid2FmZmxlLnBuZyIpKQpgYGAKClRoZSBbYHdhZmZsZWBdKGh0dHBzOi8vZ2l0aHViLmNvbS9ocmJybXN0ci93YWZmbGUpIHBhY2thZ2UgaXMgb25lIFIKaW1wbGVtZW50YXRpb24gb2YgdGhpcyBpZGVhLgoKQ3VycmVudGx5IHRoZSBkZXZlbG9wbWVudCB2ZXJzaW9uIG9uIEdpdEh1YiBpcyBuZWVkZWQgZm9yIHRoZQpmb2xsb3dpbmcgZXhhbXBsZXMuCgpTaG93aW5nIHRoZSBjb3VudHM6CgpgYGB7ciwgZmlnLndpZHRoID0gNywgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmxpYnJhcnkod2FmZmxlKQpzdG9waWZub3QocGFja2FnZVZlcnNpb24oIndhZmZsZSIpID49ICIxLjAuMSIpCmdncGxvdChhcnJhbmdlKGFnZywgSGFpciksIGFlcyh2YWx1ZXMgPSBuLCBmaWxsID0gSGFpcikpICsKICAgIGdlb21fd2FmZmxlKG5fcm93cyA9IDE4LCBmbGlwID0gVFJVRSwgY29sb3IgPSAid2hpdGUiLCBzaXplID0gMC4zMywKICAgICAgICAgICAgICAgIG5hLnJtID0gRkFMU0UpICsKICAgIGNvb3JkX2VxdWFsKCkgKwogICAgZmFjZXRfd3JhcCh+IFNleCkgKwogICAgc2NhbGVfZmlsbF9tYW51YWwodmFsdWVzID0gaGNvbHMpICsKICAgIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZV9lbmhhbmNlX3dhZmZsZSgpCmBgYAoKYGBge3IsIGV2YWwgPSBUUlVFLCBlY2hvID0gRkFMU0V9CmdncGxvdChhcnJhbmdlKGFnZywgSGFpciksIGFlcyh2YWx1ZXMgPSBuLCBmaWxsID0gSGFpcikpICsKICAgIGdlb21fd2FmZmxlKG5fcm93cyA9IDEwLCBmbGlwID0gVFJVRSwgY29sb3IgPSAid2hpdGUiLCBzaXplID0gMC4zMywKICAgICAgICAgICAgICAgIG5hLnJtID0gRkFMU0UpICsKICAgIGNvb3JkX2VxdWFsKCkgKwogICAgZmFjZXRfZ3JpZChTZXggfiBFeWUpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGhjb2xzKSArCiAgICB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWVfZW5oYW5jZV93YWZmbGUoKQpgYGAKClNob3dpbmcgdGhlIHByb3BvcnRpb25zOgoKYGBge3IsIGZpZy53aWR0aCA9IDcsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpyb3VuZF9wY3QgPC0gZnVuY3Rpb24obikgewogICAgcGN0IDwtIDEwMCAqIChuIC8gc3VtKG4pKQogICAgbm4gPC0gZmxvb3IocGN0KQogICAgaWYgKHN1bShubikgPCAxMDApIHsKICAgICAgICByZW0gPC0gcGN0IC0gbm4KICAgICAgICBpZHggPC0gc29ydChvcmRlcihyZW0pLCBkZWNyZWFzaW5nID0gVFJVRSlbc2VxX2xlbigxMDAgLSBzdW0obm4pKV0KICAgICAgICBubltpZHhdIDwtIG5uW2lkeF0gKyAxCiAgICB9CiAgICBubgp9Cgpncm91cF9ieShhZ2csIFNleCkgfD4KICAgIG11dGF0ZShwY3QgPSByb3VuZF9wY3QobikpIHw+CiAgICB1bmdyb3VwKCkgfD4KICAgIGdncGxvdChhZXModmFsdWVzID0gcGN0LCBmaWxsID0gSGFpcikpICsKICAgIGdlb21fd2FmZmxlKG5fcm93cyA9IDEwLCBmbGlwID0gVFJVRSwgY29sb3IgPSAid2hpdGUiLCBzaXplID0gMC4zMywKICAgICAgICAgICAgICAgIG5hLnJtID0gRkFMU0UpICsKICAgIGNvb3JkX2VxdWFsKCkgKwogICAgZmFjZXRfd3JhcCh+IFNleCkgKwogICAgc2NhbGVfZmlsbF9tYW51YWwodmFsdWVzID0gaGNvbHMpICsKICAgIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZV9lbmhhbmNlX3dhZmZsZSgpCmBgYAoKYGBge3IsIGV2YWwgPSBGQUxTRSwgZWNobyA9IEZBTFNFfQpncm91cF9ieShhZ2csIFNleCwgRXllKSB8PgogICAgbXV0YXRlKHBjdCA9IHJvdW5kX3BjdChuKSkgfD4KICAgIHVuZ3JvdXAoKSB8PgogICAgYXJyYW5nZShwY3QsIEhhaXIpIHw+CiAgICBnZ3Bsb3QoYWVzKHZhbHVlcyA9IHBjdCwgZmlsbCA9IEhhaXIpKSArCiAgICBnZW9tX3dhZmZsZShuX3Jvd3MgPSAxMCwgZmxpcCA9IFRSVUUsIGNvbG9yID0gIndoaXRlIiwgc2l6ZSA9IDAuMzMsCiAgICAgICAgICAgICAgICBuYS5ybSA9IEZBTFNFKSArCiAgICBjb29yZF9lcXVhbCgpICsKICAgIGZhY2V0X2dyaWQoU2V4IH4gRXllKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBoY29scykgKwogICAgdGhlbWVfbWluaW1hbCgpICsKICAgIHRoZW1lX2VuaGFuY2Vfd2FmZmxlKCkKYGBgCgoKIyMgUG9wdWxhdGlvbiBQeXJhbWlkcwoKQmFyIGNoYXJ0cyBmb3IgdHdvIGdyb3VwcyBjYW4gYmUgc2hvd24gYmFjayB0byBiYWNrLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQptdXRhdGUoYWdnLCBIYWlyID0gcmVvcmRlcihIYWlyLCBuLCBzdW0pKSB8PgogICAgZ2dwbG90KGFlcyh4ID0gaWZlbHNlKFNleCA9PSAiTWFsZSIsIG4sIC1uKSwKICAgICAgICAgICAgICAgeSA9IEhhaXIsCiAgICAgICAgICAgICAgIGZpbGwgPSBTZXgpKSArCiAgICBnZW9tX2NvbCgpICsKICAgIHhsYWIoIkNvdW50IikgKwogICAgdGhtCmBgYAoKVGhpcyBpcyBvZnRlbiB1c2VkIGZvciBzaG93aW5nIGFnZSBkaXN0cmlidXRpb25zIGJ5IHNleCBmb3IKcG9wdWxhdGlvbnM7IHRoZSByZXN1bHQgaXMgY2FsbGVkIGEgW19wb3B1bGF0aW9uCnB5cmFtaWRfXShodHRwczovL3d3dy52aXN1YWxjYXBpdGFsaXN0LmNvbS91cy1wb3B1bGF0aW9uLXB5cmFtaWQtMTk4MC0yMDUwLykuCgpBZ2UgZGlzdHJpYnV0aW9uIGRhdGEgZm9yIG1hbnkgY291bnRyaWVzIGFuZCB5ZWFycyBpcyBhdmFpbGFibGUgZnJvbSBhCltDZW5zdXMgQnVyZWF1CndlYnNpdGVdKGh0dHBzOi8vd3d3LmNlbnN1cy5nb3YvZGF0YS10b29scy9kZW1vL2lkYi8pLgoKRGF0YSBmaWxlcyBmb3IgMjAyMCBmb3IKW0dlcm1hbnldKGh0dHBzOi8vc3RhdC51aW93YS5lZHUvfmx1a2UvZGF0YS9nZXJtYW55LTIwMjAuY3N2KSBhbmQKW05pZ2VyaWFdKGh0dHBzOi8vc3RhdC51aW93YS5lZHUvfmx1a2UvZGF0YS9uaWdlcmlhLTIwMjAuY3N2KSBhcmUKYXZhaWxhYmxlIGxvY2FsbHkuCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmlmICghIGZpbGUuZXhpc3RzKCJnZXJtYW55LTIwMjAuY3N2IikpCiAgICBkb3dubG9hZC5maWxlKCJodHRwczovL3N0YXQudWlvd2EuZWR1L35sdWtlL2RhdGEvZ2VybWFueS0yMDIwLmNzdiIsCiAgICAgICAgICAgICAgICAgICJnZXJtYW55LTIwMjAuY3N2IikKaWYgKCEgZmlsZS5leGlzdHMoIm5pZ2VyaWEtMjAyMC5jc3YiKSkKICAgIGRvd25sb2FkLmZpbGUoImh0dHBzOi8vc3RhdC51aW93YS5lZHUvfmx1a2UvZGF0YS9uaWdlcmlhLTIwMjAuY3N2IiwKICAgICAgICAgICAgICAgICAgIm5pZ2VyaWEtMjAyMC5jc3YiKQoKZ21fcG9wIDwtIHJlYWQuY3N2KCJnZXJtYW55LTIwMjAuY3N2Iiwgc2tpcCA9IDEpIHw+CiAgICBmaWx0ZXIoQWdlICE9ICJUb3RhbCIpIHw+CiAgICBtdXRhdGUoQWdlID0gZmN0X2lub3JkZXIoQWdlKSkKCm5pX3BvcCA8LSByZWFkLmNzdigibmlnZXJpYS0yMDIwLmNzdiIsIHNraXAgPSAxKSB8PgogICAgZmlsdGVyKEFnZSAhPSAiVG90YWwiKSB8PgogICAgbXV0YXRlKEFnZSA9IGZjdF9pbm9yZGVyKEFnZSkpCmBgYAoKQ29tYmluaW5nIHRoZSBkYXRhIHNldHMgYWxsb3dzIGEgc2lkZSBieSBzaWRlIGNvbXBhcmlzb24gb2YgdGhlIGNvdW50czoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeSh0aWR5cikKcG9wMiA8LQogICAgYmluZF9yb3dzKG11dGF0ZShnbV9wb3AsIENvdW50cnkgPSAiR2VybWFueSIpLAogICAgICAgICAgICAgIG11dGF0ZShuaV9wb3AsIENvdW50cnkgPSAiTmlnZXJpYSIpKSB8PgogICAgc2VsZWN0KEFnZSwKICAgICAgICAgICBNYWxlID0gTWFsZS5Qb3B1bGF0aW9uLAogICAgICAgICAgIEZlbWFsZSA9IEZlbWFsZS5Qb3B1bGF0aW9uLCBDb3VudHJ5KSB8PgogICAgcGl2b3RfbG9uZ2VyKE1hbGUgOiBGZW1hbGUsCiAgICAgICAgICAgICAgICAgbmFtZXNfdG8gPSAiU2V4IiwKICAgICAgICAgICAgICAgICB2YWx1ZXNfdG8gPSAibiIpCgpnZ3Bsb3QocG9wMikgKwogICAgZ2VvbV9jb2woYWVzKHggPSBpZmVsc2UoU2V4ID09ICJNYWxlIiwgbiwgLW4pLAogICAgICAgICAgICAgICAgIHkgPSBBZ2UsCiAgICAgICAgICAgICAgICAgZmlsbCA9IFNleCkpICsKICAgIGZhY2V0X3dyYXAofiBDb3VudHJ5KSArCiAgICBzY2FsZV94X2NvbnRpbnVvdXMoCiAgICAgICAgbGFiZWxzID0gZnVuY3Rpb24obikgc2NhbGVzOjpjb21tYShhYnMobikpKSArCiAgICB4bGFiKCJDb3VudCIpICsKICAgIHRobSArCiAgICB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAidG9wIikKYGBgCgpUaGUgZGlmZmVyZW50IHNoYXBlcyBhcmUgZXZpZGVudCwgYnV0IGFyZSBoYXJkZXIgdG8gc2VlIHRoYW4KdGhleSBjb3VsZCBiZSBiZWNhdXNlIG9mIHRoZSBkaWZmZXJlbmNlIGluIHRvdGFsIHBvcHVsYXRpb246CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9Cmdyb3VwX2J5KHBvcDIsIENvdW50cnkpIHw+CiAgICBzdW1tYXJpemUoUG9wdWxhdGlvbiA9IHN1bShuKSkgfD4KICAgIHVuZ3JvdXAoKSB8PgogICAgbXV0YXRlKFBvcHVsYXRpb24gPSBzY2FsZXM6OmNvbW1hKFBvcHVsYXRpb24pKSB8PgogICAga25pdHI6OmthYmxlKGZvcm1hdCA9ICJodG1sIiwgYWxpZ24gPSAibHIiKSB8PgogICAga2FibGVFeHRyYTo6a2FibGVfc3R5bGluZyhmdWxsX3dpZHRoID0gRkFMU0UpCmBgYAoKVXNpbmcgYSBncm91cCBtdXRhdGUgd2UgY2FuIGNvbXB1dGUgc2V4L2FnZSBncm91cCBwZXJjZW50YWdlcyB3aXRoaW4KZWFjaCBjb3VudHJ5OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpncm91cF9ieShwb3AyLCBDb3VudHJ5KSB8PgogICAgbXV0YXRlKHBjdCA9IDEwMCAqIG4gLyBzdW0obikpIHw+CiAgICB1bmdyb3VwKCkgfD4KICAgIGdncGxvdCgpICsKICAgIGdlb21fY29sKGFlcyh4ID0gaWZlbHNlKFNleCA9PSAiTWFsZSIsIHBjdCwgLXBjdCksCiAgICAgICAgICAgICAgICAgeSA9IEFnZSwKICAgICAgICAgICAgICAgICBmaWxsID0gU2V4KSkgKwogICAgZmFjZXRfd3JhcCh+IENvdW50cnkpICsKICAgIHNjYWxlX3hfY29udGludW91cygKICAgICAgICBsYWJlbHMgPSBmdW5jdGlvbih4KSBzY2FsZXM6OnBlcmNlbnQoYWJzKHggLyAxMDApKSkgKwogICAgeGxhYigiUGVyY2VudCIpICsKICAgIHRobSArCiAgICB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAidG9wIikKYGBgCgpgYGB7ciwgZXZhbCA9IEZBTFNFLCBlY2hvID0gRkFMU0V9CnAgPC0gZ2dwbG90KGdtX3BvcCkgKwogICAgZ2VvbV9jb2woYWVzKHggPSBNYWxlLlBvcHVsYXRpb24sIHkgPSBBZ2UsIGZpbGwgPSAiTWFsZSIpKSArCiAgICBnZW9tX2NvbChhZXMoeCA9IC1GZW1hbGUuUG9wdWxhdGlvbiwgeSA9IEFnZSwgZmlsbCA9ICJGZW1hbGUiKSkgKwogICAgdGhtCgpwIHwgKHAgJSslIG5pX3BvcCkKYGBgCgoKIyMgTXVsdGlwbGUgQ2F0ZWdvcmljYWwgVmFyaWFibGVzCgpWaXN1YWxpemluZyB0aGUgZGlzdHJpYnV0aW9uIG9mIG11bHRpcGxlIGNhdGVnb3JpY2FsIHZhcmlhYmxlcwppbnZvbHZlcyB2aXN1YWxpemluZyBjb3VudHMgYW5kIHByb3BvcnRpb25zLgoKRGlzdHJpYnV0aW9ucyBjYW4gYmUgdmlld2VkIGFzCgoqIGpvaW50IGRpc3RyaWJ1dGlvbnM7CgoqIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMuCgpXaGVuIG9uZSB2YXJpYWJsZSAob3Igc2V2ZXJhbCkgY2FuIGJlIHZpZXdlZCBhcyBhIHJlc3BvbnNlIGFuZCBvdGhlcnMKYXMgcHJlZGljdG9ycyB0aGVuIGl0IGlzIGNvbW1vbiB0byBmb2N1cyBvbiB0aGUgY29uZGl0aW9uYWwKZGlzdHJpYnV0aW9uIG9mIHRoZSByZXNwb25zZSBnaXZlbiB0aGUgcHJlZGljdG9ycy4KClRoZSBtb3N0IGNvbW1vbiBhcHByb2FjaGVzIHVzZSB2YXJpYW50cyBvZiBiYXIgYW5kIGFyZWEgY2hhcnRzLgoKVGhlIHJlc3VsdGluZyBwbG90cyBhcmUgb2Z0ZW4gY2FsbGVkIFtfbW9zYWljCnBsb3RzX10oaHR0cHM6Ly9lbi53aWtpcGVkaWEub3JnL3dpa2kvTW9zYWljX3Bsb3QpLgoKCiMjIFR3byBEYXRhIFNldHMKCgojIyMgSGFpciBhbmQgRXllIENvbG9yCgpgYGB7cn0KSGFpckV5ZUNvbG9yREYgPC0KICAgIGFzLmRhdGEuZnJhbWUoSGFpckV5ZUNvbG9yKQpoZWFkKEhhaXJFeWVDb2xvckRGKQpgYGAKCk1hcmdpbmFsIGRpc3RyaWJ1dGlvbnMgb2YgdGhlIHZhcmlhYmxlczoKCmBgYHtyLCBmaWcuaGVpZ2h0ID0gMywgZmlnLndpZHRoID0gOSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAxIDwtIGdncGxvdChIYWlyRXllQ29sb3JERikgKwogICAgZ2VvbV9jb2woYWVzKFNleCwgRnJlcSksIGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgdGhtCnAyIDwtIG11dGF0ZShIYWlyRXllQ29sb3JERiwgSGFpciA9IHJlb3JkZXIoSGFpciwgLUZyZXEsIHN1bSkpIHw+CiAgICBnZ3Bsb3QoKSArCiAgICBnZW9tX2NvbChhZXMoSGFpciwgRnJlcSksIGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgdGhtCnAzIDwtIGdncGxvdChIYWlyRXllQ29sb3JERikgKwogICAgZ2VvbV9jb2woYWVzKEV5ZSwgRnJlcSksIGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgdGhtCnAxIHwgcDIgfCBwMwpgYGAKCgojIyMgQXJ0aHJpdGlzIERhdGEKClRoZSBgdmNkYCBwYWNrYWdlIGluY2x1ZGVzIHRoZSBkYXRhIGZyYW1lIGBBcnRocml0aXNgIHdpdGggc2V2ZXJhbAp2YXJpYWJsZXMgZm9yIDg0IHBhdGllbnRzIGluIGEgY2xpbmljYWwgdHJpYWwgZm9yIGEgdHJlYXRtZW50IGZvcgpyaGV1bWF0b2lkIGFydGhyaXRpcy4KCmBgYHtyLCBtZXNzYWdlID0gRkFMU0V9CmRhdGEoQXJ0aHJpdGlzLCBwYWNrYWdlID0gInZjZCIpCmhlYWQoQXJ0aHJpdGlzKQpgYGAKCiogVGhlIGBJbXByb3ZlZGAgdmFyaWFibGUgaXMgdGhlIHJlc3BvbnNlLgoKKiBUaGUgcHJlZGljdG9ycyBhcmUgYFRyZWF0bWVudGAsIGBTZXhgLCBhbmQgYEFnZWAuCgpDb3VudHMgZm9yIHRoZSBjYXRlZ29yaWNhbCBwcmVkaWN0b3JzOgpgYGB7cn0KeHRhYnMofiBTZXgsIEFydGhyaXRpcykKYGBgCgpgYGB7cn0KeHRhYnMofiBUcmVhdG1lbnQsIEFydGhyaXRpcykKYGBgCgpgYGB7cn0KeHRhYnMofiBUcmVhdG1lbnQgKyBTZXgsIGRhdGEgPSBBcnRocml0aXMpCmBgYAoKSm9pbnQgZGlzdHJpYnV0aW9uIG9mIHRoZSBwcmVkaWN0b3JzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoQXJ0aHJpdGlzKSArCiAgICBnZW9tX2hpc3RvZ3JhbShhZXMoeCA9IEFnZSksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDEwLAogICAgICAgICAgICAgICAgICAgZmlsbCA9ICJkZWVwc2t5Ymx1ZTMiLAogICAgICAgICAgICAgICAgICAgY29sb3IgPSAiYmxhY2siKSArCiAgICBmYWNldF9ncmlkKFRyZWF0bWVudCB+IFNleCkgKwogICAgdGhtCmBgYAoKQ29uZGl0aW9uYWwgZGlzdHJpYnVpdG9uIG9mIGFnZSwgZ2l2ZW4gc2V4IGFuZCB0cmVhdG1lbnQ6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChBcnRocml0aXMpICsKICAgIGdlb21faGlzdG9ncmFtKGFlcyh4ID0gQWdlLAogICAgICAgICAgICAgICAgICAgICAgIHkgPSBhZnRlcl9zdGF0KGRlbnNpdHkpKSwKICAgICAgICAgICAgICAgICAgIGJpbndpZHRoID0gMTAsCiAgICAgICAgICAgICAgICAgICBmaWxsID0gImRlZXBza3libHVlMyIsCiAgICAgICAgICAgICAgICAgICBjb2xvciA9ICJibGFjayIpICsKICAgIGZhY2V0X2dyaWQoVHJlYXRtZW50IH4gU2V4KSArCiAgICB0aG0KYGBgCgoKIyMgQmFyIENoYXJ0cwoKCiMjIyBIYWlyIGFuZCBFeWUgQ29sb3IKCkRlZmF1bHQgYmFyIGNoYXJ0cyBzaG93IHRoZSBpbmRpdmlkdWFsIGNvdW50IG9yIGpvaW50IHByb3BvcnRpb25zLgoKRm9yIHRoZSBoYWlyLWV5ZSBjb2xvciBhZ2dyZWdhdGVkIGRhdGEgY291bnRzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoSGFpckV5ZUNvbG9yREYpICsKICAgIGdlb21fY29sKGFlcyh4ID0gRXllLCB5ID0gRnJlcSwgZmlsbCA9IFNleCkpICsKICAgIGZhY2V0X3dyYXAofiBIYWlyKSArCiAgICB0aG0KYGBgCgpKb2ludCBwcm9wb3J0aW9uczoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KG11dGF0ZShIYWlyRXllQ29sb3JERiwgUHJvcCA9IEZyZXEgLyBzdW0oRnJlcSkpKSArCiAgICBnZW9tX2NvbChhZXMoeCA9IEV5ZSwgeSA9IFByb3AsIGZpbGwgPSBTZXgpKSArCiAgICBmYWNldF93cmFwKH4gSGFpcikgKwogICAgdGhtCmBgYAoKKiBEaWZmZXJpbmcgZnJlcXVlbmNpZXMgb2YgdGhlIGhhaXIgY29sb3JzIGFyZSB2aXNpYmxlLgoKKiBDb25kaXRpb25hbCBkaXN0cmlidXRpb25zIG9mIGV5ZSBjb2xvciB3aXRoaW4gaGFpciBjb2xvciBhcmUKICBoYXJkZXIgdG8gY29tcGFyZS4KClNob3dpbmcgY29uZGl0aW9uYWwgZGlzdHJpYnV0aW9ucyByZXF1aXJlcyBjb21wdXRpbmcgcHJvcG9ydGlvbnMKd2l0aGluIGdyb3Vwcy4KCkZvciB0aGUgam9pbnQgY29uZGl0aW9uYWwgZGlzdHJpYnV0aW9uIG9mIHNleCBhbmQgZXllIGNvbG9yIGdpdmVuIGhhaXIgY29sb3I6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9Cmdyb3VwX2J5KEhhaXJFeWVDb2xvckRGLCBIYWlyKSB8PgogICAgbXV0YXRlKFByb3AgPSBGcmVxIC8gc3VtKEZyZXEpKSB8PgogICAgdW5ncm91cCgpIHw+CiAgICBnZ3Bsb3QoKSArCiAgICBnZW9tX2NvbChhZXMoeCA9IEV5ZSwgeSA9IFByb3AsIGZpbGwgPSBTZXgpKSArCiAgICBmYWNldF93cmFwKH4gSGFpcikgKwogICAgdGhtCmBgYAoKKiBJdCBpcyBlYXNpZXIgdG8gY29tcGFyZSB0aGUgc2tld25lc3Mgb2YgdGhlIGV5ZSBjb2xvcgogIGRpc3RyaWJ1dGlvbnMgZm9yIGJsYWNrLCBicm93biwgYW5kIHJlZCBoYWlyLgoKKiBBc3Nlc3NpbmcgdGhlIHByb3BvcnRpb24gb2YgZmVtYWxlcyBvciBtYWxlcyB3aXRoaW5nIHRoZSBkaWZmZXJlbnQKICBncm91cHMgaXMgcG9zc2libGUgYnV0IGNoYWxsZW5naW5nIHNpbmNlIGl0IHJlcXVpcmVzIHJlbGF0aXZlCiAgbGVuZ3RoIGNvbXBhcmlzb25zLgoKVG8gbW9yZSBjbGVhcmx5IHNlZSB0aGUgdGhhdCB0aGUgcHJvcG9ydGlvbiBvZiBmZW1hbGVzIGFtb25nIHN1YmplY3RzCndpdGggYmxvbmQgaGFpciBhbmQgYmx1ZSBleWVzIGlzIGhpZ2hlciB0aGFuIGZvciBvdGhlciBoYWlyL2V5ZSBjb2xvcgpjb21iaW5hdGlvbnMgd2UgY2FuIGxvb2sgYXQgdGhlIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbiBvZiBzZXggZ2l2ZW4KaGFpciBhbmQgZXllIGNvbG9yLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpncm91cF9ieShIYWlyRXllQ29sb3JERiwgSGFpciwgRXllKSB8PgogICAgbXV0YXRlKFByb3AgPSBGcmVxIC8gc3VtKEZyZXEpKSB8PgogICAgdW5ncm91cCgpIHw+CiAgICBnZ3Bsb3QoKSArCiAgICBnZW9tX2NvbChhZXMoeCA9IEV5ZSwKICAgICAgICAgICAgICAgICB5ID0gUHJvcCwKICAgICAgICAgICAgICAgICBmaWxsID0gU2V4KSkgKwogICAgZmFjZXRfd3JhcCh+IEhhaXIsIG5yb3cgPSAxKSArCiAgICB0aG0gKwogICAgdGhlbWUoYXhpcy50ZXh0LnggPQogICAgICAgICAgICAgIGVsZW1lbnRfdGV4dChhbmdsZSA9IDQ1LAogICAgICAgICAgICAgICAgICAgICAgICAgICBoanVzdCA9IDEpKQpgYGAKClRoaXMgcGxvdCBjYW4gYWxzbyBiZSBvYnRhaW5lZCB1c2luZyBgcG9zaXRpb24gPSAiZmlsbCJgLgoKYGBge3IsIGV2YWwgPSBGQUxTRSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChIYWlyRXllQ29sb3JERikgKwogICAgZ2VvbV9jb2woYWVzKHggPSBFeWUsCiAgICAgICAgICAgICAgICAgeSA9IEZyZXEsCiAgICAgICAgICAgICAgICAgZmlsbCA9IFNleCksCiAgICAgICAgICAgICBwb3NpdGlvbiA9ICJmaWxsIikgKwogICAgZmFjZXRfd3JhcCh+IEhhaXIsIG5yb3cgPSAxKSArCiAgICB0aG0gKwogICAgdGhlbWUoYXhpcy50ZXh0LnggPQogICAgICAgICAgICAgIGVsZW1lbnRfdGV4dChhbmdsZSA9IDQ1LAogICAgICAgICAgICAgICAgICAgICAgICAgICBoanVzdCA9IDEpKQpgYGAKCk9uZSBkcmF3YmFjazogVGhpcyB2aXN1YWxpemF0aW9uIG5vIGxvbmdlciBzaG93cyB0aGF0IHNvbWUgb2YgdGhlCmhhaXIvZXllIGNvbG9yIGNvbWJpbmF0aW9ucyBhcmUgbW9yZSBjb21tb24gdGhhbiBvdGhlcnMuCgoKIyMjIEFydGhyaXRpcyBEYXRhCgpGb3IgdGhlIHJhdyBhcnRocml0aXMgZGF0YSwgYGdlb21fYmFyYCBjb21wdXRlcyB0aGUgYWdncmVnYXRlIGNvdW50cwphbmQgcHJvZHVjZXMgYSBzdGFja2VkIGJhciBjaGFydCBieSBkZWZhdWx0OgoKYGBge3J9CnAgPC0gZ2dwbG90KEFydGhyaXRpcywgYWVzKHggPSBTZXgsCiAgICAgICAgICAgICAgICAgICAgICAgICAgIGZpbGwgPSBJbXByb3ZlZCkpICsKICAgIGZhY2V0X3dyYXAofiBUcmVhdG1lbnQpCnAgKyBnZW9tX2JhcigpICsKICAgIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiQmx1ZXMiKSArCiAgICB0aG0KCmBgYAoKU3BlY2lmeWluZyBgcG9zaXRpb24gPSAiZG9kZ2UiYCBwcm9kdWNlcyBhIHNpZGUtYnktc2lkZSBwbG90OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwICsgZ2VvbV9iYXIocG9zaXRpb24gPSAiZG9kZ2UiKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIikgKwogICAgdGhtCmBgYAoKVGhlcmUgYXJlIG5vIGNhc2VzIG9mIG1hbGUgcGF0aWVudHMgb24gcGxhY2VibyByZXBvcnRpbmcgYFNvbWVgCmltcHJvdmVtZW50LCByZXN1bHRpbmcgaW4gd2lkZXIgYmFycyBmb3IgdGhlIG90aGVyIG9wdGlvbnMuCgpPbmUgd2F5IHRvIHByb2R1Y2UgYSB6ZXJvIGhlaWdodCBiYXI6CgoqIGFnZ3JlZ2F0ZSB3aXRoIGBjb3VudGAsIGFuZAoKKiB1c2UgYGNvbXBsZXRlYCBmcm9tIGB0aWR5cmAKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeSh0aWR5cikKY29tcF9jb3VudHMgPC0KICAgIGNvdW50KEFydGhyaXRpcywKICAgICAgICAgIFRyZWF0bWVudCwgU2V4LCBJbXByb3ZlZCkgfD4KICAgIGNvbXBsZXRlKFRyZWF0bWVudCwgU2V4LCBJbXByb3ZlZCwKICAgICAgICAgICAgIGZpbGwgPSBsaXN0KG4gPSAwKSkKZ2dwbG90KGNvbXBfY291bnRzLAogICAgICAgYWVzKHggPSBTZXgsIHkgPSBuLCBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBnZW9tX2NvbChwb3NpdGlvbiA9ICJkb2RnZSIpICsKICAgIGZhY2V0X3dyYXAofiBUcmVhdG1lbnQpICsKICAgIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiQmx1ZXMiKSArCiAgICB0aG0KYGBgCgpBbm90aGVyIG9wdGlvbiBpcyB0byB1c2UgdGhlIGBwcmVzZXJ2ZSA9ICJzaW5nbGUiYCBvcHRpb24gd2l0aApgcG9zaXRpb25fZG9kZ2VgLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwICsgZ2VvbV9iYXIocG9zaXRpb24gPQogICAgICAgICAgICAgICAgIHBvc2l0aW9uX2RvZGdlKAogICAgICAgICAgICAgICAgICAgICBwcmVzZXJ2ZSA9ICJzaW5nbGUiKSkgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJCbHVlcyIpICsKICAgIHRobQpgYGAKClNob3dpbmcgY29uZGl0aW9uYWwgZGlzdHJpYnV0aW9ucyBvZiBgSW1wcm92ZWRgIGdpdmVuIGRpZmZlcmVudCBsZXZlbHMKb2YgYFRyZWF0bWVudGAgYW5kIGBTZXhgOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpncm91cF9ieShjb21wX2NvdW50cywgVHJlYXRtZW50LCBTZXgpIHw+CiAgICBtdXRhdGUocHJvcCA9IG4gLyBzdW0obikpIHw+CiAgICB1bmdyb3VwKCkgfD4KICAgIGdncGxvdCgpICsKICAgIGdlb21fY29sKGFlcyh4ID0gU2V4LAogICAgICAgICAgICAgICAgIHkgPSBwcm9wLAogICAgICAgICAgICAgICAgIGZpbGwgPSBJbXByb3ZlZCksCiAgICAgICAgICAgICBwb3NpdGlvbiA9ICJkb2RnZSIpICsKICAgIGZhY2V0X3dyYXAofiBUcmVhdG1lbnQpICsKICAgIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiQmx1ZXMiKSArCiAgICB0aG0KYGBgCgpTdGFja2VkIGJhciBjaGFydHMgd2l0aCBoZWlnaHQgb25lIGFyZSBhbm90aGVyIG9wdGlvbiB0byBtYWtlCnRoZXNlIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMgZWFzaWVyIHRvIGNvbXBhcmU6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgKyBnZW9tX2Jhcihwb3NpdGlvbiA9ICJmaWxsIikgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJCbHVlcyIpICsKICAgIHRobQpgYGAKCk9yZGVyaW5nIG9mIHZhcmlhYmxlcyBhZmZlY3RzIHdoaWNoIGNvbXBhcmlzb25zIGFyZSBlYXNpZXIuCgoqIEEgcmVzZWFyY2hlciBtaWdodCB3YW50IHRvIGVtcGhhc2l6ZSB0aGUgZGlmZmVyZW50aWFsIHJlc3BvbnNlIGFtb25nCiAgbWFsZXMgYW5kIGZlbWFsZXMuCgoqIEEgcGF0aWVudCBtaWdodCBwcmVmZXIgdG8gYmUgYWJsZSB0byBmb2N1cyBvbiB3aGV0aGVyIHRoZSB0cmVhdG1lbnQKICBpcyBlZmZlY3RpdmUgZm9yIHRoZW06CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChBcnRocml0aXMsIGFlcyh4ID0gVHJlYXRtZW50LCBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBnZW9tX2Jhcihwb3NpdGlvbiA9ICJmaWxsIikgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJCbHVlcyIpICsKICAgIHRobSArCiAgICBmYWNldF93cmFwKH4gU2V4KQpgYGAKClNvbWUgbm90ZXM6CgoqIFRoZSBzdGFja2VkIGJhciBjaGFydCBpcyBlZmZlY3RpdmUgZm9yIHR3byBjYXRlZ29yaWVzLCBhbmQgYSBmZXcKICBtb3JlIGlmIHRoZXkgYXJlIG9yZGVyZWQuCgoqIFByb3ZpZGluZyBhIHZpc3VhbCBpbmRpY2F0aW9uIG9mIHVuY2VydGFpbnR5IGluIHRoZSBlc3RpbWF0ZXMgaXMgYQogIGNoYWxsZW5nZS4gVGhlIHN0YW5kYXJkIGVycm9ycyBpbiB0aGlzIGNhc2UgYXJlIGFyb3VuZCAwLjEuCgoqIFRoZSBwcm9wb3J0aW9ucyBvZiBlYWNoIHRyZWF0bWVudCBncm91cCB0aGF0IGFyZSBtYWxlIG9yIGZlbWFsZQogIGNvdWxkIGJlIGVuY29kZWQgaW4gdGhlIGJhciB3aWR0aHMuCgoqIFRoZSByZXN1bHRpbmcgcGxvdCBpcyBjYWxsZWQgYSBfc3BpbmUgcGxvdF8uCgoqIEJhc2ljIGBnZ3Bsb3QyYCBkb2VzIG5vdCBzZWVtIHRvIG1ha2UgdGhpcyBlYXN5LgoKCiMjIFNwaW5lIFBsb3RzCgpfU3BpbmUgcGxvdHNfIGFyZSBhIHNwZWNpYWwgY2FzZSBvZiBbX21vc2FpYwpwbG90c19dKGh0dHBzOi8vZW4ud2lraXBlZGlhLm9yZy93aWtpL01vc2FpY19wbG90KSwgYW5kIGNhbiBiZSBzZWVuIGFzCmEgZ2VuZXJhbGl6YXRpb24gb2Ygc3RhY2tlZCBiYXIgcGxvdHMuCgpGb3IgYSBzcGluZSBwbG90IHRoZSBwcm9wb3J0aW9ucyBmb3IgdGhlIGNhdGVnb3JpZXMgb2YgYSBwcmVkaWN0b3IKdmFyaWFibGUgYXJlIGVuY29kZWQgaW4gdGhlIGJhciB3aWR0aHMuCgpUaGUgYGdnbW9zYWljYCBwYWNrYWdlIHByb3ZpZGVzIHN1cHBvcnQgZm9yIG1vc2FpYyBwbG90cyBpbiB0aGUKYGdncGxvdGAgZnJhbWV3b3JrLiAoSXQgY2FuIGJlIGEgbGl0dGxlIHJvdWdoIGFyb3VuZCB0aGUgZWRnZXMuKQoKU3BpbmUgcGxvdHMgYXJlIHByb3ZpZGVkIGJ5IHRoZSBiYXNlIGdyYXBoaWNzIGZ1bmN0aW9uIGBzcGluZXBsb3RgIGFuZAp0aGUgYHZjZGAgZnVuY3Rpb24gYHNwaW5lYC4KCmB2Y2RgIHBsb3RzIGFyZSBidWlsdCBvbiB0aGUgYGdyaWRgIGdyYXBoaWNzIHN5c3RlbSwgbGlrZSBgbGF0dGljZWAKYW5kIGBnZ3Bsb3QyYCBncmFwaGljcy4KCjwhLS0gc3BpbmUgcGxvdCBpbiB0aGUgd2lsZDoKaHR0cHM6Ly90LmNvLzkxeHFrV1hJZkQ7CmluIGltZy9lbmVyZ3ktc3BpbmUucG5nIC0tPgoKQSBzcGluZSBwbG90IGZvciB0aGUgZGlzdHJpYnV0aW9uIG9mIGBJbXByb3ZlZGAgZ2l2ZW4gYFNleGAgaW4gdGhlCmBUcmVhdGVkYCBncm91cDoKCmBgYHtyLCB3YXJuaW5nID0gRkFMU0UsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpsaWJyYXJ5KGdnbW9zYWljKQpmaWx0ZXIoQXJ0aHJpdGlzLCBUcmVhdG1lbnQgPT0gIlRyZWF0ZWQiKSB8PgogICAgbXV0YXRlKEltcHJvdmVkID0gZmN0X3JldihJbXByb3ZlZCkpIHw+CiAgICBnZ3Bsb3QoKSArCiAgICBnZW9tX21vc2FpYyhhZXMoeCA9IHByb2R1Y3QoU2V4KSwKICAgICAgICAgICAgICAgICAgICBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIiwKICAgICAgICAgICAgICAgICAgICAgIGRpcmVjdGlvbiA9IC0xLAogICAgICAgICAgICAgICAgICAgICAgZ3VpZGUgPSBndWlkZV9sZWdlbmQocmV2ZXJzZSA9IFRSVUUpKSArCiAgICBmYWNldF93cmFwKH4gVHJlYXRtZW50KSArCiAgICB0aG0gKyBsYWJzKHggPSAiIiwgeSA9ICJJbXByb3ZlZCIpCmBgYAoKU3BpbmUgcGxvdHMgZm9yIGBUcmVhdG1lbnRgIGdyb3VwcyB1c2luZyBmYWNldGluZzoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShnZ21vc2FpYykKbXV0YXRlKEFydGhyaXRpcywKICAgICAgIEltcHJvdmVkID0gZmN0X3JldihJbXByb3ZlZCkpIHw+CiAgICBnZ3Bsb3QoKSArCiAgICBnZW9tX21vc2FpYyhhZXMoeCA9IHByb2R1Y3QoU2V4KSwKICAgICAgICAgICAgICAgICAgICBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIiwKICAgICAgICAgICAgICAgICAgICAgIGRpcmVjdGlvbiA9IC0xLAogICAgICAgICAgICAgICAgICAgICAgZ3VpZGUgPSBndWlkZV9sZWdlbmQocmV2ZXJzZSA9IFRSVUUpKSArCiAgICBmYWNldF93cmFwKH4gVHJlYXRtZW50KSArCiAgICB0aG0gKyBsYWJzKHggPSAiIiwgeSA9ICJJbXByb3ZlZCIpCmBgYAoKU3BpbmUgcGxvdHMgZm9yIHRoZSBhcnRocml0aXMgZGF0YSwgZmFjZXRlZCBvbiBgU2V4YDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShnZ21vc2FpYykKbXV0YXRlKEFydGhyaXRpcywKICAgICAgIEltcHJvdmVkID0gZmN0X3JldihJbXByb3ZlZCkpIHw+CiAgICBnZ3Bsb3QoKSArCiAgICBnZW9tX21vc2FpYyhhZXMoeCA9IHByb2R1Y3QoVHJlYXRtZW50KSwKICAgICAgICAgICAgICAgICAgICBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIiwKICAgICAgICAgICAgICAgICAgICAgIGRpcmVjdGlvbiA9IC0xLAogICAgICAgICAgICAgICAgICAgICAgZ3VpZGUgPSBndWlkZV9sZWdlbmQocmV2ZXJzZSA9IFRSVUUpKSArCiAgICBmYWNldF93cmFwKH4gU2V4KSArCiAgICB0aG0gKyBsYWJzKHggPSAiIiwgeSA9ICJJbXByb3ZlZCIpCmBgYApUaGlzIG5vIGxvbmdlciBzaG93cyB0aGUgRmVtYWxlL01hbGUgaW1iYWxhbmNlLgoKRm9yIGFnZ3JlZ2F0ZSBjb3VudHMgdXNlIHRoZSB3ZWlnaHQgYWVzdGhldGljOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQptdXRhdGUoSGFpckV5ZUNvbG9yREYsIFNleCA9IGZjdF9yZXYoU2V4KSkgfD4KICAgIGdncGxvdCgpICsKICAgIGdlb21fbW9zYWljKGFlcyh3ZWlnaHQgPSBGcmVxLAogICAgICAgICAgICAgICAgICAgIHggPSBwcm9kdWN0KEhhaXIpLAogICAgICAgICAgICAgICAgICAgIGZpbGwgPSBTZXgpKSArCiAgICB0aG0gKyBsYWJzKHggPSAiSGFpciIsIHkgPSAiIikKYGBgCgpTcGluZSBwbG90cyBvZiBgU2V4YCB3aXRoaW4gYEV5ZWAgY29sb3IsIGZhY2V0ZWQgb24gYEhhaXJgIGNvbG9yOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQptdXRhdGUoSGFpckV5ZUNvbG9yREYsIFNleCA9IGZjdF9yZXYoU2V4KSkgfD4KICAgIGdncGxvdCgpICsKICAgIGdlb21fbW9zYWljKGFlcyh3ZWlnaHQgPSBGcmVxLAogICAgICAgICAgICAgICAgICAgIHggPSBwcm9kdWN0KEV5ZSksCiAgICAgICAgICAgICAgICAgICAgZmlsbCA9IFNleCkpICsKICAgIHRobSArIGxhYnMoeCA9ICJFeWUiLCB5ID0gIiIpICsKICAgIGZhY2V0X3dyYXAofiBIYWlyLAogICAgICAgICAgICAgICBucm93ID0gMSwKICAgICAgICAgICAgICAgc2NhbGVzID0gImZyZWVfeCIpICsKICAgIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJ0b3AiLAogICAgICAgICAgYXhpcy50ZXh0LnkgPSBlbGVtZW50X2JsYW5rKCksCiAgICAgICAgICBheGlzLnRleHQueCA9CiAgICAgICAgICAgICAgZWxlbWVudF90ZXh0KGFuZ2xlID0gNDUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgIGhqdXN0ID0gMSkpICsKICAgIHNjYWxlX3lfY29udGludW91cyhleHBhbmQgPSBjKDAsIDApKQpgYGAKClRoZSByZWxhdGl2ZSBzaXplcyBvZiB0aGUgZ3JvdXBzIG9uIHRoZSBgeGAgKGV5ZSBjb2xvcikgYXhpcyBhcmUgc2hvd24Kd2l0aGluIHRoZSBmYWNldHMuCgpUaGUgc2l6ZXMgb2YgdGhlIGZhY2V0ZWQgdmFyaWFibGUgKGhhaXIgY29sb3IpIGdyb3VwcyBhcmUgbm90IHJlZmxlY3RlZC4KCl9Eb3VibGUgZGVja2VyIHBsb3RzXyB0cnkgdG8gYWRkcmVzcyB0aGlzLgoKCiMjIERvdWJsZWRlY2tlciBQbG90cwoKX0RvdWJsZWRlY2tlciBwbG90c18gY2FuIGJlIHZpZXdlZCBhcyBhIGdlbmVyYWxpemF0aW9uIG9mIHNwaW5lIHBsb3RzCnRvIG11bHRpcGxlIHByZWRpY3RvcnMuCgpQYWNrYWdlIGB2Y2RgIHByb3ZpZGVzIHRoZSBgZG91YmxlZGVja2VyYCBmdW5jdGlvbi4KClRoaXMgZnVuY3Rpb24gY2FuIHVzZSBhIGZvcm11bGEgaW50ZXJmYWNlLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQphcnRoX3BhbCA8LQogICAgUkNvbG9yQnJld2VyOjpicmV3ZXIucGFsKDMsICJCbHVlcyIpCmFydGhfZ3AgPC0gZ3JpZDo6Z3BhcihmaWxsID0gYXJ0aF9wYWwpCnZjZDo6ZG91YmxlZGVja2VyKEltcHJvdmVkIH4gVHJlYXRtZW50ICsgU2V4LAogICAgICAgICAgICAgICAgICBkYXRhID0gQXJ0aHJpdGlzLAogICAgICAgICAgICAgICAgICBncCA9IGFydGhfZ3AsCiAgICAgICAgICAgICAgICAgIG1hcmdpbnMgPSBjKDIsIDUsIDQsIDIpKQpgYGAKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KdmNkOjpkb3VibGVkZWNrZXIoSW1wcm92ZWQgfiBTZXggKyBUcmVhdG1lbnQsCiAgICAgICAgICAgICAgICAgIGRhdGEgPSBBcnRocml0aXMsCiAgICAgICAgICAgICAgICAgIGdwID0gYXJ0aF9ncCwKICAgICAgICAgICAgICAgICAgbWFyZ2lucyA9IGMoMiwgNSwgNCwgMikpCmBgYAoKVXNpbmcgYGdnbW9zYWljYDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbXV0YXRlKEFydGhyaXRpcywKICAgICAgIEltcHJvdmVkID0gZmN0X3JldihJbXByb3ZlZCkpIHw+CiAgICBnZ3Bsb3QoKSArCiAgICBnZW9tX21vc2FpYygKICAgICAgICBhZXMoeCA9IHByb2R1Y3QoU2V4LCBUcmVhdG1lbnQpLAogICAgICAgICAgICBmaWxsID0gSW1wcm92ZWQpLAogICAgICAgIGRpdmlkZXIgPSBkZGVja2VyKCkpICsKICAgIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiQmx1ZXMiLAogICAgICAgICAgICAgICAgICAgICAgZGlyZWN0aW9uID0gLTEsCiAgICAgICAgICAgICAgICAgICAgICBndWlkZSA9IGd1aWRlX2xlZ2VuZChyZXZlcnNlID0gVFJVRSkpICsKICAgIHRobSArCiAgICB0aGVtZShheGlzLnRleHQueCA9CiAgICAgICAgICAgICAgZWxlbWVudF90ZXh0KGFuZ2xlID0gMTUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgIGhqdXN0ID0gMSkpICsKICAgIGxhYnMoeCA9ICIiLCB5ID0gIiIpCmBgYAoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQptdXRhdGUoQXJ0aHJpdGlzLAogICAgICAgSW1wcm92ZWQgPSBmY3RfcmV2KEltcHJvdmVkKSkgfD4KICAgIGdncGxvdCgpICsKICAgIGdlb21fbW9zYWljKAogICAgICAgIGFlcyh4ID0gcHJvZHVjdChUcmVhdG1lbnQsIFNleCksCiAgICAgICAgICAgIGZpbGwgPSBJbXByb3ZlZCksCiAgICAgICAgZGl2aWRlciA9IGRkZWNrZXIoKSkgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJCbHVlcyIsCiAgICAgICAgICAgICAgICAgICAgICBkaXJlY3Rpb24gPSAtMSwKICAgICAgICAgICAgICAgICAgICAgIGd1aWRlID0gZ3VpZGVfbGVnZW5kKHJldmVyc2UgPSBUUlVFKSkgKwogICAgdGhtICsKICAgIHRoZW1lKGF4aXMudGV4dC54ID0KICAgICAgICAgICAgICBlbGVtZW50X3RleHQoYW5nbGUgPSAxNSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgaGp1c3QgPSAxKSkgKwogICAgbGFicyh4ID0gIiIsIHkgPSAiIikKYGBgCgpBbm90aGVyIGFwcHJvYWNoIHVzaW5nIHRoZQpbYGdnaDR4YF0oaHR0cHM6Ly90ZXVuYnJhbmQuZ2l0aHViLmlvL2dnaDR4LykgcGFja2FnZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShkcGx5cikKbGlicmFyeShnZ3Bsb3QyKQpsaWJyYXJ5KGdnaDR4KQpkYXRhKEFydGhyaXRpcywgcGFja2FnZSA9ICJ2Y2QiKQpnZ3Bsb3QoQXJ0aHJpdGlzLCBhZXMoeCA9IDAsIGZpbGwgPSBJbXByb3ZlZCkpICsKICAgIGdlb21fYmFyKHBvc2l0aW9uID0gImZpbGwiKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIikgKwogICAgZmFjZXRfbmVzdGVkKH4gVHJlYXRtZW50ICsgU2V4KSArCiAgICBmb3JjZV9wYW5lbHNpemVzKGNvbHMgPSBjb3VudChBcnRocml0aXMsIFRyZWF0bWVudCwgU2V4KSRuKSArCiAgICBsYWJzKHggPSBlbGVtZW50X2JsYW5rKCksIHkgPSBlbGVtZW50X2JsYW5rKCkpICsKICAgIHNjYWxlX3hfY29udGludW91cyhleHBhbmQgPSBjKDAsIDApLCBicmVha3MgPSBOVUxMLCBsYWJlbHMgPSBOVUxMKSArCiAgICBzY2FsZV95X2NvbnRpbnVvdXMoZXhwYW5kID0gYygwLCAwKSwgYnJlYWtzID0gTlVMTCwgbGFiZWxzID0gTlVMTCkKYGBgCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmxpYnJhcnkoZHBseXIpCmxpYnJhcnkoZ2dwbG90MikKbGlicmFyeShnZ2g0eCkKZGF0YShBcnRocml0aXMsIHBhY2thZ2UgPSAidmNkIikKZ2dwbG90KEFydGhyaXRpcywgYWVzKHggPSAwLCBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBnZW9tX2Jhcihwb3NpdGlvbiA9ICJmaWxsIikgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJCbHVlcyIpICsKICAgIGZhY2V0X25lc3RlZCh+IFNleCArIFRyZWF0bWVudCkgKwogICAgZm9yY2VfcGFuZWxzaXplcyhjb2xzID0gY291bnQoQXJ0aHJpdGlzLCBTZXgsIFRyZWF0bWVudCkkbikgKwogICAgbGFicyh4ID0gZWxlbWVudF9ibGFuaygpLCB5ID0gZWxlbWVudF9ibGFuaygpKSArCiAgICBzY2FsZV94X2NvbnRpbnVvdXMoZXhwYW5kID0gYygwLCAwKSwgYnJlYWtzID0gTlVMTCwgbGFiZWxzID0gTlVMTCkgKwogICAgc2NhbGVfeV9jb250aW51b3VzKGV4cGFuZCA9IGMoMCwgMCksIGJyZWFrcyA9IE5VTEwsIGxhYmVscyA9IE5VTEwpCmBgYAoKIyMgTW9zYWljIFBsb3RzCgpfTW9zYWljIHBsb3RzXyByZWN1cnNpdmVseSBwYXJ0aXRpb24gdGhlIGF4ZXMgdG8gcmVwcmVzZW50IGNvdW50cyBvZgpjYXRlZ29yaWNhbCB2YXJpYWJsZXMgYXMgcmVjdGFuZ2xlcy4KCiogQmFzZSBncmFwaGljcyBwcm92aWRlcyBgbW9zYWljcGxvdGA7CgoqIGB2Y2RgIHByb3ZpZGVzIGBtb3NhaWNgLgoKQm90aCBzdXBwb3J0IGEgZm9ybXVsYSBpbnRlcmZhY2UuCgpBIE1vc2FpYyBwbG90IGZvciB0aGUgcHJlZGljdG9ycyBgU2V4YCBhbmQgYFRyZWF0bWVudGA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnZjZDo6bW9zYWljKH4gU2V4ICsgVHJlYXRtZW50LAogICAgICAgICAgICBkYXRhID0gQXJ0aHJpdGlzKQpgYGAKCkFkZGluZyBgSW1wcm92ZWRgIHRvIHRoZSBqb2ludCBkaXN0cmlidXRpb246CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnZjZDo6bW9zYWljKH4gU2V4ICsgVHJlYXRtZW50ICsgSW1wcm92ZWQsCiAgICAgICAgICAgIGRhdGEgPSBBcnRocml0aXMpCmBgYAoKSWRlbnRpZnlpbmcgYEltcHJvdmVkYCBhcyB0aGUgcmVzcG9uc2U6Cgo8IS0tICMjdmNkOjptb3NhaWMoSW1wcm92ZWQgfiBTZXggKyBUcmVhdG1lbnQsIGRhdGEgPSBBcnRocml0aXMsIGdwID0gYXJ0aF9ncCktLT4KCmBgYHtyfQp2Y2Q6Om1vc2FpYyhJbXByb3ZlZCB+IFNleCArIFRyZWF0bWVudCwKICAgICAgICAgICAgZGF0YSA9IEFydGhyaXRpcykKYGBgCgpNYXRjaGluZyB0aGUgZG91YmxlZGVja2VyIHBsb3RzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQp2Y2Q6Om1vc2FpYygKICAgICAgICAgSW1wcm92ZWQgfiBUcmVhdG1lbnQgKyBTZXgsCiAgICAgICAgIGRhdGEgPSBBcnRocml0aXMsCiAgICAgICAgIHNwbGl0X3ZlcnRpY2FsID0gYyhUUlVFLCBUUlVFLCBGQUxTRSkpCmBgYAoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQp2Y2Q6Om1vc2FpYygKICAgICAgICAgSW1wcm92ZWQgfiBTZXggKyBUcmVhdG1lbnQsCiAgICAgICAgIGRhdGEgPSBBcnRocml0aXMsCiAgICAgICAgIHNwbGl0X3ZlcnRpY2FsID0gYyhUUlVFLCBUUlVFLCBGQUxTRSkpCmBgYAoKU29tZSB2YXJpYW50cyB1c2luZyBgZ2dtb3NhaWNgOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QobXV0YXRlKEFydGhyaXRpcywgU2V4ID0gZmN0X3JldihTZXgpKSkgKwogICAgZ2VvbV9tb3NhaWMoCiAgICAgICAgYWVzKHggPSBwcm9kdWN0KFRyZWF0bWVudCwKICAgICAgICAgICAgICAgICAgICAgICAgU2V4KSkpICsKICAgIGNvb3JkX2ZsaXAoKSArCiAgICBsYWJzKHggPSAiIiwgeSA9ICIiKQpgYGAKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KG11dGF0ZShBcnRocml0aXMsCiAgICAgICAgICAgICAgU2V4ID0gZmN0X3JldihTZXgpLAogICAgICAgICAgICAgIEltcHJvdmVkID0gZmN0X3JldihJbXByb3ZlZCkpKSArCiAgICBnZW9tX21vc2FpYyhhZXMoeCA9IHByb2R1Y3QoSW1wcm92ZWQsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgVHJlYXRtZW50LAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIFNleCkpKSArCiAgICBjb29yZF9mbGlwKCkKYGBgCgpBIG1vc2FpYyBwbG90IGZvciBhbGwgYml2YXJpYXRlIG1hcmdpbmFsczoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcGFpcnMoeHRhYnMofiBTZXggKyBUcmVhdG1lbnQgKyBJbXByb3ZlZCwgZGF0YSA9IEFydGhyaXRpcykpCmBgYAoKCiMjIFNwaW5vZ3JhbXMgYW5kIENEIFBsb3RzCgo8IS0tIGJ1aWxkaW5nIGEgc3Bpbm9ncmFtIGZyb20gc2NyYXRjaCwgbW9yZSBvciBsZXNzOgoKYGBgcgpBcnRoIDwtIG11dGF0ZShBcnRocml0aXMsCiAgICAgICAgICAgICAgIEFnZUJpbiA9IGN1dChBZ2UsIHNlcSgyMCwgYnkgPSAxMCwgbGVuID0gNykpLAogICAgICAgICAgICAgICBJbXByb3ZlZCA9IGZjdF9yZXYoSW1wcm92ZWQpKQpkIDwtIGZpbHRlcihBcnRoLCBUcmVhdG1lbnQgPT0gIlRyZWF0ZWQiKSB8PgogICAgY291bnQoQWdlQmluKSB8PgogICAgbXV0YXRlKGJyayA9IChjdW1zdW0obGFnKG4sIGRlZmF1bHQgPSAwKSkgKyAwLjUgKiBuKSAvIHN1bShuKSkKcCA8LSBnZ3Bsb3QoZCkKCnAgKyBnZW9tX2NvbChhZXMoeCA9IEFnZUJpbiwgeSA9IG4pKQoKcDIgPC0gcCArCiAgICBnZW9tX2NvbChhZXMoeCA9IDAuNSwgeSA9IG4sIGNvbG9yID0gZmN0X3JldihBZ2VCaW4pKSwKICAgICAgICAgICAgIHBvc2l0aW9uID0gImZpbGwiLCBmaWxsID0gTkEpICsKICAgIGd1aWRlcyhjb2xvciA9ICJub25lIikgKwogICAgc2NhbGVfeV9jb250aW51b3VzKGJyZWFrcyA9IGQkYnJrLAogICAgICAgICAgICAgICAgICAgICAgIGxhYmVscyA9IGQkQWdlQmluKQpwMgoKcDIgKyBjb29yZF9mbGlwKCkKYGBgCgpgYGByCnByb3BzIDwtIGZpbHRlcihBcnRoLCBUcmVhdG1lbnQgPT0gIlRyZWF0ZWQiKSB8PgogICAgY291bnQoQWdlQmluLCBJbXByb3ZlZCkgfD4KICAgIG11dGF0ZShBZ2VCaW4gPSBmY3RfZHJvcChBZ2VCaW4pKSB8PgogICAgY29tcGxldGUoQWdlQmluLCBJbXByb3ZlZCwgZmlsbCA9IGxpc3QobiA9IDApKSB8PgogICAgZ3JvdXBfYnkoQWdlQmluKSB8PgogICAgbXV0YXRlKHByb3AgPSBuIC8gc3VtKG4pKSB8PgogICAgdW5ncm91cCgpIHw+CiAgICBzZWxlY3QoLW4pCnByb3BzCmBgYAotLT4KCl9TcGlub2dyYW1zXyBhbmQgX0NEIHBsb3RzXyBzaG93IHRoZSBjb25kaXRpb25hbCBkaXN0cmlidXRpb24gb2YgYQpjYXRlZ29yaWNhbCB2YXJpYWJsZSBnaXZlbiB0aGUgdmFsdWUgb2YgYSBudW1lcmljIHZhcmlhYmxlLgoKKiBTcGlub2dyYW1zIHVzZSB0aGUgc2FtZSBiaW5uaW5nIGFzIGEgaGlzdG9ncmFtIGFuZCB0aGVuIGNyZWF0ZSBhCiAgc3BpbmUgcGxvdC4KCiogQ0QgcGxvdHMgdXNlIGEgc21vb3RoaW5nIG9yIGRlbnNpdHkgZXN0aW1hdGlvbiBhcHByb2FjaC4KCkEgc3Bpbm9ncmFtIGZvciBgSW1wcm92ZWRgIGFnYWluc3QgYEFnZWA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CkFydGhUIDwtIGZpbHRlcihBcnRocml0aXMsCiAgICAgICAgICAgICAgICBUcmVhdG1lbnQgPT0gIlRyZWF0ZWQiKSB8PgogICAgbXV0YXRlKEltcHJvdmVkID0gZmN0X3JldihJbXByb3ZlZCkpCmFydGhUX2dwIDwtCiAgICBncmlkOjpncGFyKGZpbGwgPSByZXYoYXJ0aF9ncCRmaWxsKSkKdmNkOjpzcGluZShJbXByb3ZlZCB+IEFnZSwKICAgICAgICAgICBkYXRhID0gQXJ0aFQsCiAgICAgICAgICAgZ3AgPSBhcnRoVF9ncCwKICAgICAgICAgICBicmVha3MgPSA1KQpgYGAKCkFuIGFuYWxvZ291cyBwbG90IGNyZWF0ZWQgd2l0aCBgZ2dtb3NhaWNgIGJ5IGJpbm5pbmcgdGhlIGBBZ2VgIHZhcmlhYmxlOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpBcnRoIDwtCiAgICBtdXRhdGUoQXJ0aHJpdGlzLAogICAgICAgICAgIEFnZUJpbiA9IGN1dChBcnRocml0aXMkQWdlLAogICAgICAgICAgICAgICAgICAgICAgICBzZXEoMjAsIGJ5ID0gMTAsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICBsZW4gPSA3KSksCiAgICAgICAgICAgSW1wcm92ZWQgPSBmY3RfcmV2KEltcHJvdmVkKSkKZmlsdGVyKEFydGgsIFRyZWF0bWVudCA9PSAiVHJlYXRlZCIpIHw+CiAgICBjb3VudChJbXByb3ZlZCwgQWdlQmluKSB8PgogICAgZ2dwbG90KCkgKwogICAgZ2VvbV9tb3NhaWMoYWVzKHdlaWdodCA9IG4sCiAgICAgICAgICAgICAgICAgICAgeCA9IHByb2R1Y3QoQWdlQmluKSwKICAgICAgICAgICAgICAgICAgICBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIiwKICAgICAgICAgICAgICAgICAgICAgIGRpcmVjdGlvbiA9IC0xLAogICAgICAgICAgICAgICAgICAgICAgZ3VpZGUgPSBndWlkZV9sZWdlbmQocmV2ZXJzZSA9IFRSVUUpKSArCiAgICB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWUoYXhpcy50aXRsZSA9IGVsZW1lbnRfYmxhbmsoKSkKYGBgCgpBIGZhY2V0IGdyaWQgY2FuIGJlIHVzZWQgdG8gY3JlYXRlIHNwaW5vZ3JhbXMgZm9yIGVhY2ggb2YgdGhlCmBTZXhgL2BUcmVhdG1lbnRgIGNvbWJpbmF0aW9uczoKCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGNvdW50KEFydGgsIEltcHJvdmVkLCBTZXgsIFRyZWF0bWVudCwgQWdlQmluKSkgKwogICAgZ2VvbV9tb3NhaWMoYWVzKHdlaWdodCA9IG4sCiAgICAgICAgICAgICAgICAgICAgeCA9IHByb2R1Y3QoQWdlQmluKSwKICAgICAgICAgICAgICAgICAgICBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIiwKICAgICAgICAgICAgICAgICAgICAgIGRpcmVjdGlvbiA9IC0xLAogICAgICAgICAgICAgICAgICAgICAgZ3VpZGUgPSBndWlkZV9sZWdlbmQocmV2ZXJzZSA9IFRSVUUpKSArCiAgICB0aGVtZV9taW5pbWFsKCkgKwogICAgZmFjZXRfZ3JpZChUcmVhdG1lbnQgfiBTZXgpICsKICAgIHRoZW1lKGF4aXMudGl0bGUgPSBlbGVtZW50X2JsYW5rKCkpICsKICAgIHRoZW1lKGF4aXMudGV4dC54ID0gZWxlbWVudF90ZXh0KGFuZ2xlID0gMzUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBoanVzdCA9IDEpLAogICAgICAgICAgYXhpcy50ZXh0LnkgPSBlbGVtZW50X2JsYW5rKCkpCmBgYAoKQSBbc3Bpbm9ncmFtXShodHRwczovL2Zsb3dpbmdkYXRhLmNvbS8yMDIxLzA4LzAyL2RlY2xpbmUtb2YtdS1zLXZhY2NpbmF0aW9uLXJhdGUtY29tcGFyZWQtYWdhaW5zdC1ldXJvcGVzLykgaW4gdGhlIG1lZGlhIChOWVQsIEF1Z3VzdCAyMDIxKToKCmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI3MCUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoIlZhY2NpbmF0aW9uLXJhdGVzLXdpdGgtTWFyaW1la2tvLTE1MzZ4OTI1LnBuZyIpKQpgYGAKClNvbWUgcGxvdHMgaW4gYSBbVHdpdHRlciB0aHJlYWRdKGh0dHBzOi8vdHdpdHRlci5jb20vamJ1cm5tdXJkb2NoL3N0YXR1cy8xNTAzNDIwNjYwODY5MjE0MjEzP3M9MjAmdD1SWnhPWGlIWjBlWGtWNldYTUl1VlZBKToKCmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI5MCUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoImNvdmlkLXNwaW5vZ3JhbS5wbmciKSkKYGBgCgpgYGB7ciwgZWNobyA9IEZBTFNFLCBvdXQud2lkdGggPSAiOTAlIn0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJjb3ZpZC1tb3J0LnBuZyIpKQpgYGAKCkNEIHBsb3RzIGVzdGltYXRlIHRoZSBjb25kaXRpb25hbCBkZW5zaXR5IG9mIHRoZSBgeGAgdmFyaWFibGUgZ2l2ZW4gdGhlCmxldmVscyBvZiBgeWAsIHdlaWdodGVkIGJ5IHRoZSBtYXJnaW5hbCBwcm9wb3J0aW9ucyBvZiBgeWAgYW5kIHVzZQp0aGVzZSB0byBlc3RpbWF0ZSBjdW11bGF0aXZlIHByb2JhYmlsaXRpZXMuCgoqIFRoZSBzbGljZSBhdCBhIHBhcnRpY3VsYXIgYHhgIGxldmVsIHZpc3VhbGl6ZXMgdGhlIGNvbmRpdGlvbmFsCiAgZGlzdHJpYnV0aW9uIG9mIGB5YCBnaXZlbiBgeGAgYXQgdGhhdCBsZXZlbC4KCiogYGdlb21fZGVuc2l0eWAgd2l0aCBgcG9zaXRpb24gPSBzdGFja2AgaXMgb25lIHdheSB0byBjcmVhdGUgYSBDRAogIHBsb3QuCgoqIFRoZSBgY2RfcGxvdGAgZnVuY3Rpb24gZnJvbSB0aGUgYHZjZGAgcGFja2FnZSBwcm9kdWNlcyBhIENEIHBsb3QKICB1c2luZyBgZ3JpZGAgZ3JhcGhpY3MuCgoqIFRoZSBgY2RwbG90YCBmdW5jdGlvbiBmcm9tIHRoZSBiYXNlIGBncmFwaGljc2AgcGFja2FnZSBwcm92aWRlcyB0aGUKICBzYW1lIHBsb3RzIHVzaW5nIGJhc2UgZ3JhcGhpY3MuCgo8IS0tIEJ1aWxkaW5nIGEgQ0QgcGxvdCBpbiBzdGVwczoKYGBgcgpkIDwtIGZpbHRlcihBcnRocml0aXMsIFRyZWF0bWVudCA9PSAiVHJlYXRlZCIsIFNleCA9PSAiRmVtYWxlIikKCiMjIHVzZSB5ID0gYWZ0ZXJfc3RhdChjb3VudCkgc28gYXJlYSBpcyBudW1iZXIgb2Ygcm93cwpwMCA8LSBnZ3Bsb3QoZCwgYWVzKHggPSBBZ2UsIHkgPSBhZnRlcl9zdGF0KGNvdW50KSkpICsKICAgIGdlb21fZGVuc2l0eShidyA9IDUsIGZpbGwgPSAiZ3JleSIpCnAwCgojIyBzZXBhcmF0ZSBjb3VudC13ZWlnaHRlZCBkZW5zaXRpZXMgZm9yIGVhY2ggZ3JvdXAgd2l0aCBhbHBoYSBibGVuZGluZwpwMSA8LSBnZ3Bsb3QoZCwgYWVzKHggPSBBZ2UsIHkgPSBhZnRlcl9zdGF0KGNvdW50KSwgZmlsbCA9IEltcHJvdmVkKSkgKwogICAgZ2VvbV9kZW5zaXR5KGJ3ID0gNSwgYWxwaGEgPSAwLjUpICsKICAgIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiQmx1ZXMiKSArCiAgICBndWlkZXMoZmlsbCA9ICJub25lIikKcDEKCiMjIGVhc2llciB0byBzZWUgdGhlIHNlcGFyYXRlIGRlbnNpdGllcyB3aXRoIGZhY2V0aW5nCnAxICsgZmFjZXRfd3JhcCh+IEltcHJvdmVkKQoKIyMgc3RhY2sgdGhlIGRlbnNpdGllcwpnZ3Bsb3QoZCwgYWVzKHggPSBBZ2UsIHkgPSBhZnRlcl9zdGF0KGNvdW50KSwgZmlsbCA9IEltcHJvdmVkKSkgKwogICAgZ2VvbV9kZW5zaXR5KHBvc2l0aW9uID0gInN0YWNrIiwgYncgPSA1KSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIikgKwogICAgZ3VpZGVzKGZpbGwgPSAibm9uZSIpCgojIyByZXNjYWxlIHRvIGhlaWdodCAxIHdpdGggcG9zaXRpb24gPSAiZmlsbCIKcDIgPC0gZ2dwbG90KGQsIGFlcyh4ID0gQWdlLCB5ID0gYWZ0ZXJfc3RhdChjb3VudCksIGZpbGwgPSBJbXByb3ZlZCkpICsKICAgIGdlb21fZGVuc2l0eShwb3NpdGlvbiA9ICJmaWxsIiwgYncgPSA1KSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIikgKwogICAgZ3VpZGVzKGZpbGwgPSAibm9uZSIpCnAyCgpwMiArIGdlb21fdmxpbmUoeGludGVyY2VwdCA9IDQwLCBsdHkgPSAyKQoKcDIgKyBnZW9tX3ZsaW5lKHhpbnRlcmNlcHQgPSA2MCwgbHR5ID0gMikKYGBgCi0tPgoKQ0QgcGxvdHMgZm9yIHRoZSBgVHJlYXRlZGAgZ3JvdXA6CgpgYGB7ciwgZmlnLmhlaWdodCA9IDYsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpmaWx0ZXIoQXJ0aHJpdGlzLCBUcmVhdG1lbnQgPT0gIlRyZWF0ZWQiKSB8PgogICAgZ2dwbG90KGFlcyh4ID0gQWdlLCBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBnZW9tX2RlbnNpdHkocG9zaXRpb24gPSAiZmlsbCIsIGJ3ID0gNSkgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJCbHVlcyIpICsKICAgIGZhY2V0X3dyYXAofiBTZXgsIG5jb2wgPSAxKSArCiAgICB0aG0KYGBgCgpDRCBwbG90cyBmb3IgYWxsIGNvbWJpbmF0aW9ucyBlbmQgdXAgd2l0aCBvbmUgZ3JvdXAgb2Ygc2l6ZSBvbmUgYW5kCm9uZSBvZiBzaXplIHplcm8sIHdoaWNoIHByb2R1Y2VzIGEgbm9uLXVzZWZ1bCBwbG90IGZvciBvbmUKY29tYmluYXRpb246CgpgYGB7ciwgZmlnLndpZHRoID0gOCwgZmlnLmhlaWdodCA9IDYsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpjb3VudChBcnRocml0aXMsIFRyZWF0bWVudCwgU2V4LCBJbXByb3ZlZCkgfD4KICAgIGNvbXBsZXRlKFRyZWF0bWVudCwgU2V4LCBJbXByb3ZlZCwKICAgICAgICAgICAgIGZpbGwgPSBsaXN0KG4gPSAwKSkgfD4KICAgIGZpbHRlcihuIDwgMikKCmdncGxvdChBcnRocml0aXMsCiAgICAgICBhZXMoeCA9IEFnZSwgZmlsbCA9IEltcHJvdmVkKSkgKwogICAgZ2VvbV9kZW5zaXR5KHBvc2l0aW9uID0gImZpbGwiLCBidyA9IDUpICsKICAgIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiQmx1ZXMiKSArCiAgICBmYWNldF9ncmlkKFRyZWF0bWVudCB+IFNleCkgKwogICAgdGhtCmBgYAoKCiMjIFVuY2VydGFpbnR5IFJlcHJlc2VudGF0aW9uCgpDYXRlZ29yaWNhbCBkYXRhIGFyZSBvZnRlbiBhbmFseXplZCBieSBmaXR0aW5nIG1vZGVscyByZXByZXNlbnRpbmcKY29uZGl0aW9uYWwgaW5kZXBlbmRlbmNlIHN0cnVjdHVyZXMuCgoqIFBsb3R0aW5nIHJlc2lkdWFscyBmcm9tIHRoZXNlIG1vZGVscyBjYW4gaGVscCBhc3Nlc3MgaG93IHdlbGwgdGhleQogIGZpdC4KCiogYHZjZDo6bW9zYWljYCBzdXBwb3J0cyB1c2luZyBjb2xvciB0byByZXByZXNlbnQgbWFnbml0dWRlIG9mIHJlc2lkdWFscwogIGZvciBjb21wYXJpbmcgdG8gYSBzaW1wbGUgaW5kZXBlbmRlbmNlIG1vZGVsLgoKRm9yIHRoZSBgQXJ0aHJpdGlzYCBkYXRhLCBvYnNlcnZlZCBjb3VudHMgYW5kIGV4cGVjdGVkIGNvdW50cyB1bmRlciBhbgppbmRlcGVuZGVuY2UgbW9kZWwgYXNzdW1pbmcgYFRyZWF0bWVudGAgYW5kIGBJbXByb3ZlZGAgYXJlIGluZGVwZW5kZW50CmNhbiBiZSB2aXN1YWxpemVkIGFzIG1vc2FpYyBwbG90czoKCmBgYHtyLCBmaWcud2lkdGggPSA4LCBmaWcuaGVpZ2h0ID0gNCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CiMjIHRoZXJlIGFyZSBlYXNpZXIgd2F5cyBkbyBkbyB0aGlzIC4uLgp2IDwtIGNvdW50KEFydGhyaXRpcywgVHJlYXRtZW50LCBJbXByb3ZlZCkKcFQgPC0gZ3JvdXBfYnkodiwgVHJlYXRtZW50KSB8PgogICAgc3VtbWFyaXplKG4gPSBzdW0obikpIHw+CiAgICBtdXRhdGUocFQgPSBuIC8gc3VtKG4pKSB8PgogICAgc2VsZWN0KC1uKQpwSSA8LSBncm91cF9ieSh2LCBJbXByb3ZlZCkgfD4KICAgIHN1bW1hcml6ZShuID0gc3VtKG4pKSB8PgogICAgbXV0YXRlKHBJID0gbiAvIHN1bShuKSkgfD4KICAgIHNlbGVjdCgtbikKdiA8LSBsZWZ0X2pvaW4odiwgcFQsICJUcmVhdG1lbnQiKSB8PgogICAgbGVmdF9qb2luKHBJLCAiSW1wcm92ZWQiKSB8PgogICAgbXV0YXRlKHAgPSBwVCAqIHBJLAogICAgICAgICAgIFRyZWF0bWVudCA9IGZjdF9yZXYoVHJlYXRtZW50KSkKCnBvIDwtIGdncGxvdCh2KSArCiAgICBnZW9tX21vc2FpYyhhZXMod2VpZ2h0ID0gbiwgeCA9IHByb2R1Y3QoSW1wcm92ZWQsIFRyZWF0bWVudCksCiAgICAgICAgICAgICAgICAgICAgZmlsbCA9IEltcHJvdmVkKSkgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJCbHVlcyIpICsKICAgIGd1aWRlcyhmaWxsID0gIm5vbmUiKSArCiAgICBsYWJzKHRpdGxlID0gIk9ic2VydmVkIFByb3BvcnRpb25zIikgKwogICAgdGhtICsKICAgIGNvb3JkX2ZsaXAoKSArCiAgICB0aGVtZShheGlzLnRleHQueSA9IGVsZW1lbnRfdGV4dChhbmdsZSA9IDkwLCBoanVzdCA9IDApKQoKcGUgPC0gZ2dwbG90KHYpICsKICAgIGdlb21fbW9zYWljKGFlcyh3ZWlnaHQgPSBwLCB4ID0gcHJvZHVjdChJbXByb3ZlZCwgVHJlYXRtZW50KSwKICAgICAgICAgICAgICAgICAgICBmaWxsID0gSW1wcm92ZWQpKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIikgKwogICAgZ3VpZGVzKGZpbGwgPSAibm9uZSIpICsKICAgIGxhYnModGl0bGUgPSAiRXhwZWN0ZWQgUHJvcG9ydGlvbnMiKSArCiAgICB0aG0gKwogICAgY29vcmRfZmxpcCgpICsKICAgIHRoZW1lKGF4aXMudGV4dC55ID0gZWxlbWVudF90ZXh0KGFuZ2xlID0gOTAsIGhqdXN0ID0gMCkpCgpwbyArIHBlCmBgYAoKQSBwbG90IGZvciBhc3Nlc3NpbmcgdGhlIGZpdCBvZiB0aGUgcmVzaWR1YWxzIGJldHdlZW4gdGhlIG9ic2VydmVkIGFuZApleHBlY3RlZCBkYXRhIHVuZGVyIGEgbW9kZWwgYXNzdW1pbmcgaW5kZXBlbmRlbmNlIG9mIGBUcmVhdG1lbnRgIGFuZApgSW1wcm92ZWRgIHByb2R1Y2VzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQp2Y2Q6Om1vc2FpYyh+IFRyZWF0bWVudCArIEltcHJvdmVkLAogICAgICAgICAgICBkYXRhID0gQXJ0aHJpdGlzLAogICAgICAgICAgICBncCA9IHZjZDo6c2hhZGluZ19tYXgpCmBgYAoKQW5vdGhlciB2aXN1YWxpemF0aW9uIG9mIHRoZSByZXNpZHVhbHMgaXMgdGhlIF9hc3NvY2lhdGlvbiBwbG90Xwpwcm9kdWNlZCBieSBgYXNzb2NgOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQp2Y2Q6OmFzc29jKH4gVHJlYXRtZW50ICsgSW1wcm92ZWQsCiAgICAgICAgICAgZGF0YSA9IEFydGhyaXRpcywKICAgICAgICAgICBncCA9IHZjZDo6c2hhZGluZ19tYXgpCmBgYAoKCiMjIFJlZmVyZW5jZXMKCj4gVGhlIHZpZ25ldHRlIFtfUmVzaWR1YWwtQmFzZWQgU2hhZGluZ3MgaW4KPiB2Y2RfXShodHRwczovL2NyYW4uci1wcm9qZWN0Lm9yZy9wYWNrYWdlPXZjZC92aWduZXR0ZXMvcmVzaWR1YWwtc2hhZGluZ3MucGRmKQo+IGluIHRoZSBgdmNkYCBwYWNrYWdlLgoKPiBaZWlsZWlzLCBBY2hpbSwgRGF2aWQgTWV5ZXIsIGFuZCBLdXJ0IEhvcm5pay4gIlJlc2lkdWFsLWJhc2VkCj4gc2hhZGluZ3MgZm9yIHZpc3VhbGl6aW5nIChjb25kaXRpb25hbCkgaW5kZXBlbmRlbmNlLiIgSm91cm5hbCBvZgo+IENvbXB1dGF0aW9uYWwgYW5kIEdyYXBoaWNhbCBTdGF0aXN0aWNzIDE2LCBuby4gMyAoMjAwNyk6IDUwNy01MjUuCgo+IFRoZSB2aWduZXR0ZSBbX1dvcmtpbmcgd2l0aCBjYXRlZ29yaWNhbCBkYXRhIHdpdGggUiBhbmQgdGhlIHZjZCBhbmQKICB2Y2RFeHRyYQogIHBhY2thZ2VzX10oaHR0cHM6Ly93d3cuZGF0YXZpcy5jYS9jb3Vyc2VzL1ZDRC92Y2QtdHV0b3JpYWwucGRmKQogIGluIHRoZSBgdmNkRXh0cmFgIHBhY2thZ2UuCgpTZXZlcmFsIG90aGVyIGV4cGVyaW1lbnRhbCBtb3NhaWMgcGxvdCBpbXBsZW1lbnRhdGlvbnMgYXJlIGF2YWlsYWJsZQpmb3IgYGdncGxvdGAuCgoKIyMgU29tZSBPdGhlciBWaXN1YWxpemF0aW9ucwoKCiMjIyBUcmVlIE1hcHMKClRyZWUgbWFwcyBzaG93IGhpZXJhcmNoaWNhbGx5IHN0cnVjdHVyZWQgKG9yIHRyZWUtdHJ1Y3R1cmVkKSBkYXRhLgoKKiBFYWNoIGJyYW5jaCBpcyByZXByZXNlbnRlZCBieSBhIHJlY3RhbmdsZS4KCiogTGVhZiBub2RlIHRpbGVzIGhhdmUgYXJlYXMgcHJvcG9ydGlvbmFsIHRvIHRoZSB2YWx1ZSBvZiBhIHZhcmlhYmxlLgoKKiBUaWxlcyBhcmUgb2Z0ZW4gY29sb3JlZCB0byByZWZsZWN0IHRoZSB2YWx1ZSBvZiBhbm90aGVyIHZhcmlhYmxlLgoKVGhlIHBhY2thZ2UgYHRyZWVtYXBpZnlgIHByb3ZpZGVzIGEgYGdncGxvdGAtYmFzZWQgaW1wbGVtZW50YXRpb24uCgpUaGUgZGF0YSBzZXQgYEcyMGAgaW5jbHVkZXMgc29tZSB2YXJpYWJsZXMgb24gdGhlIEctMjAgbWVtYmVyIGNvdW50cmllczoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeSh0cmVlbWFwaWZ5KQpzZWxlY3QoRzIwLCByZWdpb24sCiAgICAgICBjb3VudHJ5LCBnZHBfbWlsX3VzZCwgaGRpKSB8PgogICAga25pdHI6OmthYmxlKGZvcm1hdCA9ICJodG1sIikgfD4KICAgIGthYmxlRXh0cmE6OmthYmxlX3N0eWxpbmcoCiAgICAgICAgICAgICAgICAgICAgZnVsbF93aWR0aCA9IEZBTFNFKQpgYGAKCkEgc2ltcGxlIHRyZWUgd2l0aCBvbmx5IG9uZSBsZXZlbCwgdGhlIGluZGl2aWR1YWwgY291bnRyaWVzOgoKYGBge3IsIGluY2x1ZGUgPSBGQUxTRX0KbGlicmFyeShub21ub21sKQpgYGAKPCEtLQoKIyBub2xpbnQgc3RhcnQKLS0+CjxjZW50ZXI+CmBgYHtub21ub21sLCBlY2hvID0gRkFMU0V9CiNwYWRkaW5nOiAyNQojZm9udHNpemU6IDE4CiNsaW5ld2lkdGg6IDIKI2RpcmVjdGlvbjogZG93bgoKW1Jvb3RdIC0+IFtHZXJtYW55XQpbUm9vdF0gLT4gW0ZyYW5jZV0KW1Jvb3RdIC0+IFtKYXBhbl0KW1Jvb3RdIC0+IFtDaGluYV0KW1Jvb3RdIC0+IFsuLi5dCmBgYAo8L2NlbnRlcj4KPCEtLQoKIyBub2xpbnQgZW5kCi0tPgoKQSBjb3JyZXNwb25kaW5nIHRyZWUgbWFwIGJhc2VkIG9uIGBnZHBfbWlsX3VzZGA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChHMjAsIGFlcyhhcmVhID0gZ2RwX21pbF91c2QpKSArCiAgICBnZW9tX3RyZWVtYXAoKSArCiAgICBnZW9tX3RyZWVtYXBfdGV4dChhZXMobGFiZWwgPSBjb3VudHJ5KSwKICAgICAgICAgICAgICAgICAgICAgIGNvbG9yID0gIndoaXRlIikKYGBgCgpBIHRyZWUgZ3JvdXBpbmcgYnkgcmVnaW9uOgoKPGNlbnRlcj4KYGBge25vbW5vbWwsIGVjaG8gPSBGQUxTRX0KI3BhZGRpbmc6IDI1CiNmb250c2l6ZTogMTgKI2xpbmV3aWR0aDogMgojZGlyZWN0aW9uOiBkb3duCgpbUm9vdF0gLT4gW0V1cm9wZV0KW1Jvb3RdIC0+IFtBc2lhXQpbUm9vdF0gLT4gWy4uLl0KW0V1cm9wZV0gLT4gW0dlcm1hbnldCltFdXJvcGVdIC0+IFtGcmFuY2VdCltFdXJvcGVdIC0+IFsuLi4uXQpbQXNpYV0gLT4gW0phcGFuXQpbQXNpYV0gLT4gW0NoaW5hXQpbQXNpYV0gLT4gWy4uLi4uXQoKYGBgCjwvY2VudGVyPgoKQSBjb3JyZXNwb25kaW5nIHRyZWUgbWFwOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoRzIwLCBhZXMoYXJlYSA9IGdkcF9taWxfdXNkLAogICAgICAgICAgICAgICAgc3ViZ3JvdXAgPSByZWdpb24pKSArCiAgICBnZW9tX3RyZWVtYXAoKSArCiAgICBnZW9tX3RyZWVtYXBfdGV4dChhZXMobGFiZWwgPSBjb3VudHJ5KSwKICAgICAgICAgICAgICAgICAgICAgIGNvbG9yID0gIndoaXRlIikgKwogICAgZ2VvbV90cmVlbWFwX3N1Ymdyb3VwX2JvcmRlcigKICAgICAgICBjb2xvciA9ICJyZWQiKSArCiAgICBnZW9tX3RyZWVtYXBfc3ViZ3JvdXBfdGV4dChjb2xvciA9ICJyZWQiKQpgYGAKCkEgdHJlZSBtYXAgc2hvd2luZyBHRFAgdmFsdWVzIGZvciB0aGUgRy0yMCBtZW1iZXJzLCBncm91cGVkIGJ5IHJlZ2lvbiwKd2l0aCBmaWxsIG1hcHBlZCB0byB0aGUgY291bnRyeSdzIEh1bWFuIERldmVsb3BtZW50IEluZGV4OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoRzIwLCBhZXMoYXJlYSA9IGdkcF9taWxfdXNkLAogICAgICAgICAgICAgICAgZmlsbCA9IGhkaSwKICAgICAgICAgICAgICAgIHN1Ymdyb3VwID0gcmVnaW9uKSkgKwogICAgZ2VvbV90cmVlbWFwKCkgKwogICAgZ2VvbV90cmVlbWFwX3RleHQoYWVzKGxhYmVsID0gY291bnRyeSksCiAgICAgICAgICAgICAgICAgICAgICBjb2xvciA9ICJ3aGl0ZSIpICsKICAgIGdlb21fdHJlZW1hcF9zdWJncm91cF9ib3JkZXIoKSArCiAgICBnZW9tX3RyZWVtYXBfc3ViZ3JvdXBfdGV4dCgKICAgICAgICBjb2xvciA9ICJsaWdodGdyZXkiKQpgYGAKCkEgdHJlZW1hcCByZXByZXNlbnRpbmcgdGhlIGRpc3RyaWJ1dGlvbiBvZiBleWUgY29sb3Igd2l0aGluIGhhaXIgY29sb3I6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9Cmdyb3VwX2J5KGFnZywgRXllLCBIYWlyKSB8PgogICAgc3VtbWFyaXplKG4gPSBzdW0obikpIHw+CiAgICB1bmdyb3VwKCkgfD4KICAgIGdncGxvdChhZXMoYXJlYSA9IG4sCiAgICAgICAgICAgICAgIHN1Ymdyb3VwID0gSGFpcikpICsKICAgIGdlb21fdHJlZW1hcChhZXMoZmlsbCA9IEV5ZSksCiAgICAgICAgICAgICAgICAgY29sb3IgPSAid2hpdGUiKSArCiAgICBnZW9tX3RyZWVtYXBfc3ViZ3JvdXBfdGV4dCgpICsKICAgIGdlb21fdHJlZW1hcF9zdWJncm91cF9ib3JkZXIoCiAgICAgICAgY29sb3IgPSAiYmxhY2siLCBzaXplID0gNikgKwogICAgZ2VvbV90cmVlbWFwX3RleHQoYWVzKGxhYmVsID0gRXllKSwKICAgICAgICAgICAgICAgICAgICAgIGNvbG9yID0gImdyZXk5MCIpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGVjb2xzKSArCiAgICBndWlkZXMoZmlsbCA9ICJub25lIikKYGBgCgpBIHRyZWVtYXAgcmVwcmVzZW50aW5nIHByb3BvcnRpb25zIGZvciBgSW1wcm92ZWRgIHdpdGhpbiBgVHJlYXRtZW50YAp3aXRoaW4gYFNleGAgZm9yIHRoZSBBcnRocml0aXMgZGF0YToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KY291bnQoQXJ0aCwgVHJlYXRtZW50LCBJbXByb3ZlZCwgU2V4KSB8PgogICAgZ2dwbG90KGFlcyhhcmVhID0gbiwKICAgICAgICAgICAgICAgc3ViZ3JvdXAgPSBTZXgsIGZpbGwgPSBJbXByb3ZlZCwKICAgICAgICAgICAgICAgc3ViZ3JvdXAyID0gVHJlYXRtZW50KSkgKwogICAgZ2VvbV90cmVlbWFwKCkgKwogICAgZ2VvbV90cmVlbWFwX3N1Ymdyb3VwX3RleHQoKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIkJsdWVzIiwKICAgICAgICAgICAgICAgICAgICAgIGRpcmVjdGlvbiA9IC0xKSArCiAgICBnZW9tX3RyZWVtYXBfc3ViZ3JvdXBfYm9yZGVyKCkgKwogICAgZ2VvbV90cmVlbWFwX3N1Ymdyb3VwMl90ZXh0KHBsYWNlID0gInRvcCIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgc2l6ZSA9IDIwKQpgYGAKCgojIyMgQWxsdXZpYWwgcGxvdHMKClRoZXNlIGFyZSBhbHNvIGtub3duIGFzCgoqIF9wYXJhbGxlbCBzZXRzXywgb3IKCiogX1NhbmtleSBkaWFncmFtc18uCgpUaGV5IGNhbiBiZSB2aWV3ZWQgYXMgYSBwYXJhbGxlbCBjb29yZGluYXRlcyBwbG90IGZvciBjYXRlZ29yaWNhbCBkYXRhLgoKU2V2ZXJhbCBpbXBsZW1lbnRhdGlvbnMgYXJlIGF2YWlsYWJsZSwgaW5jbHVkaW5nOgoKPCEtLSAqIGBhbGx1dmlhbGAgdXNpbmcgYmFzZSBncmFwaGljczsgLS0+CgoqIGBnZW9tX3BhcmFsbGVsX3NldHNgIGZyb20gYGdnZm9yY2VgOwoKKiBgZ2VvbV9zYW5rZXlgIGZyb20gW2BnZ3NhbmtleWBdKGh0dHBzOi8vZ2l0aHViLmNvbS9kYXZpZHNqb2JlcmcvZ2dzYW5rZXkpOwoKKiBgZ2VvbV9hbGx1dml1bWAgZnJvbSBgZ2dhbGx1dmlhbGAuCgo8IS0tIEhhaXIvRXllIGNvbG9yIHVzaW5nIHRoZSBgYWxsdXZpYWxgIHBhY2thZ2U6IC0tPgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgZXZhbCA9IEZBTFNFfQpIREYgPC0gbXV0YXRlKEhhaXJFeWVDb2xvckRGLCBTZXggPSBmY3RfcmV2KFNleCkpCmxpYnJhcnkoYWxsdXZpYWwpCnBhbCA8LSBSQ29sb3JCcmV3ZXI6OmJyZXdlci5wYWwoMywgIlNldDEiKQp3aXRoKEhERiwKICAgICBhbGx1dmlhbChIYWlyLCBFeWUsIFNleCwgZnJlcSA9IEZyZXEsIGNvbCA9IHBhbFthcy5udW1lcmljKFNleCldKSkKYGBgCgpIYWlyL0V5ZSBjb2xvciB1c2luZyB0aGUgYGdnZm9yY2VgIHBhY2thZ2U6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnBhbCA8LSBSQ29sb3JCcmV3ZXI6OmJyZXdlci5wYWwoMywgIlNldDEiKQpIREYgPC0gbXV0YXRlKEhhaXJFeWVDb2xvckRGLAogICAgICAgICAgICAgIFNleCA9IGZjdF9yZXYoU2V4KSkKbGlicmFyeShnZ2ZvcmNlKQpzSERGIDwtIGdhdGhlcl9zZXRfZGF0YShIREYsIDMgOiAxKQpzSERGIDwtIG11dGF0ZShzSERGLCB4ID0gZmN0X2lub3JkZXIoYXMuZmFjdG9yKHgpKSkgIyoqKiogc2ltcGxpZnkgdGhpcz8KZ2dwbG90KHNIREYsIGFlcyh4LCBpZCA9IGlkLAogICAgICAgICAgICAgICAgIHNwbGl0ID0geSwKICAgICAgICAgICAgICAgICB2YWx1ZSA9IEZyZXEpKSArCiAgICBnZW9tX3BhcmFsbGVsX3NldHMoYWVzKGZpbGwgPSBTZXgpLAogICAgICAgICAgICAgICAgICAgICAgIGFscGhhID0gMC41LAogICAgICAgICAgICAgICAgICAgICAgIGF4aXMud2lkdGggPSAwLjEpICsKICAgIGdlb21fcGFyYWxsZWxfc2V0c19heGVzKAogICAgICAgIGF4aXMud2lkdGggPSAwLjEpICsKICAgIGdlb21fcGFyYWxsZWxfc2V0c19sYWJlbHMoCiAgICAgICAgY29sb3VyID0gJ3doaXRlJykgKwogICAgc2NhbGVfZmlsbF9tYW51YWwoCiAgICAgICAgdmFsdWVzID0gYyhNYWxlID0gcGFsWzJdLAogICAgICAgICAgICAgICAgICAgRmVtYWxlID0gcGFsWzFdKSkgKwogICAgdGhlbWVfdm9pZCgpICsgZ3VpZGVzKGZpbGwgPSAibm9uZSIpCmBgYAoKPCEtLSBBcnRocml0aXMgZGF0YSB3aXRoIGBhbGx1dmlhbGA6IC0tPgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgZXZhbCA9IEZBTFNFfQp3aXRoKGNvdW50KEFydGgsIEltcHJvdmVkLCBUcmVhdG1lbnQsIFNleCksCiAgICAgYWxsdXZpYWwoSW1wcm92ZWQsIFRyZWF0bWVudCwgU2V4LCBmcmVxID0gbiwgY29sID0gcGFsW2FzLm51bWVyaWMoU2V4KV0pKQpgYGAKCkFydGhyaXRpcyBkYXRhIHdpdGggYGdnZm9yY2VgOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpzQXJ0aCA8LSBtdXRhdGUoQXJ0aCwKICAgICAgICAgICAgICAgIEltcHJvdmVkID0gZmFjdG9yKEltcHJvdmVkLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgb3JkZXJlZCA9IEZBTFNFKSkgfD4KICAgIGNvdW50KEltcHJvdmVkLCBUcmVhdG1lbnQsIFNleCkgfD4KICAgIGdhdGhlcl9zZXRfZGF0YSgzIDogMSkKc0FydGggPC0gbXV0YXRlKHNBcnRoLAogICAgICAgICAgICAgICAgeCA9IGZjdF9pbm9yZGVyKGZhY3Rvcih4KSksCiAgICAgICAgICAgICAgICBTZXggPSBmY3RfcmV2KFNleCkpCmdncGxvdChzQXJ0aCwgYWVzKHgsCiAgICAgICAgICAgICAgICAgIGlkID0gaWQsCiAgICAgICAgICAgICAgICAgIHNwbGl0ID0geSwKICAgICAgICAgICAgICAgICAgdmFsdWUgPSBuKSkgKwogICAgZ2VvbV9wYXJhbGxlbF9zZXRzKGFlcyhmaWxsID0gU2V4KSwKICAgICAgICAgICAgICAgICAgICAgICBhbHBoYSA9IDAuNSwKICAgICAgICAgICAgICAgICAgICAgICBheGlzLndpZHRoID0gMC4xKSArCiAgICBnZW9tX3BhcmFsbGVsX3NldHNfYXhlcyhheGlzLndpZHRoID0gMC4xKSArCiAgICBnZW9tX3BhcmFsbGVsX3NldHNfbGFiZWxzKAogICAgICAgIGNvbG91ciA9ICd3aGl0ZScpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKAogICAgICAgIHZhbHVlcyA9IGMoTWFsZSA9IHBhbFsyXSwKICAgICAgICAgICAgICAgICAgIEZlbWFsZSA9IHBhbFsxXSkpICsKICAgIHRoZW1lX3ZvaWQoKSArIGd1aWRlcyhmaWxsID0gIm5vbmUiKQpgYGAKCmBgYHtyLCBldmFsID0gRkFMU0UsIGVjaG8gPSBGQUxTRX0KIyMgcmVmdWdlZSBkYXRhIChuZWVkcyBhZGp1c3RpbmcgdGV4dCBzaXplcyBvciBsYWJlbHMpCiMjIGNvdWxkIGFsc28gdHJ5IGNob3JkIGRpYWdyYW0KUiA8LSBjb3VudChyZWYuZHRsLCBEZXN0aW5hdGlvbiwgTmF0aW9uYWxpdHksIHd0ID0gQ2FzZXMpCm5hdHMgPC0gKGNvdW50KFIsIE5hdGlvbmFsaXR5LCB3dCA9IG4pIHw+IHNsaWNlX21heChuLCBuID0gMTApKSROYXRpb25hbGl0eQpkc3RzIDwtIChjb3VudChSLCBEZXN0aW5hdGlvbiwgd3QgPSBuKSB8PiBzbGljZV9tYXgobiwgbiA9IDEwKSkkRGVzdGluYXRpb24KbXV0YXRlKFIsIE5hdGlvbmFsaXR5ID0gZmN0X290aGVyKE5hdGlvbmFsaXR5LCBrZWVwID0gbmF0cyksCiAgICAgICBEZXN0aW5hdGlvbiA9IGZjdF9vdGhlcihEZXN0aW5hdGlvbiwga2VlcCA9IGRzdHMpKSB8PgogICAgZ2F0aGVyX3NldF9kYXRhKDEgOiAyKSB8PgogICAgZ2dwbG90KGFlcyh4LCBpZCA9IGlkLCBzcGxpdCA9IHksIHZhbHVlID0gbikpICsKICAgIGdlb21fcGFyYWxsZWxfc2V0cyhhZXMoZmlsbCA9IE5hdGlvbmFsaXR5KSwgYWxwaGEgPSAwLjUsIGF4aXMud2lkdGggPSAwLjEpICsKICAgIGdlb21fcGFyYWxsZWxfc2V0c19heGVzKGF4aXMud2lkdGggPSAwLjEpICsKICAgIGdlb21fcGFyYWxsZWxfc2V0c19sYWJlbHMoY29sb3VyID0gJ3doaXRlJywgc2l6ZSA9IDMpICsKICAgIHRoZW1lX3ZvaWQoKSArIGd1aWRlcyhmaWxsID0gIm5vbmUiKQpgYGAKCgojIyMgU3RyZWFtIEdyYXBocwoKW1N0cmVhbQogIGdyYXBoc10oaHR0cHM6Ly93d3cudmlzdWFsaXNpbmdkYXRhLmNvbS8yMDEwLzA4L21ha2luZy1zZW5zZS1vZi1zdHJlYW1ncmFwaHMvKQogIGFyZSBhIGdlbmVyYWxpemF0aW9uIG9mIHN0YWNrZWQgYmFyIGNoYXJ0cyBwbG90dGVkIGFnYWluc3QgYSBudW1lcmljCiAgdmFyaWFibGUuCgpJbiBzb21lIGNhc2VzIHRoZSBvcmlnaW5zIG9mIHRoZSBiYXJzIGFyZSBzaGlmdGVkIHRvIGltcHJvdmUgc29tZQphc3BlY3Qgb2YgdGhlIG92ZXJhbGwgdmlzdWFsaXphdGlvbi4KCkFuIGVhcmx5IGV4YW1wbGUgaXMgdGhlIFtCYWJ5IE5hbWUKVm95YWdlcl0oaHR0cHM6Ly93d3cuYmV3aXRjaGVkLmNvbS9uYW1ldm95YWdlci5odG1sKS4KKEEgbW9yZSByZWNlbnQgdmFyaWFudCBpcyBhbHNvClthdmFpbGFibGVdKGh0dHBzOi8vbmFtZXJvbG9neS5jb20vYmFieS1uYW1lLWdyYXBoZXIvKS4pCgpBIFtOWSBUaW1lcwp2aXN1YWxpemF0aW9uXShodHRwczovL2FyY2hpdmUubnl0aW1lcy5jb20vd3d3Lm55dGltZXMuY29tL2ludGVyYWN0aXZlLzIwMDgvMDIvMjMvbW92aWVzLzIwMDgwMjIzX1JFVkVOVUVfR1JBUEhJQy5odG1sP19yPTApCm9mIG1vdmllIGJveCBvZmZpY2UgcmVzdWx0cyBpcyBhbm90aGVyIGV4YW1wbGUuIChbQmxvZyBwb3N0IHdpdGggYQpzdGF0aWMKdmVyc2lvbl0oaHR0cHM6Ly9mbG93aW5nZGF0YS5jb20vMjAwOC8wMi8yNS9lYmItYW5kLWZsb3ctb2YtYm94LW9mZmljZS1yZWNlaXB0cy1vdmVyLXBhc3QtMjAteWVhcnMvKSkuCgpTb21lIFIgaW1wbGVtZW50YXRpb25zIG9uIEdpdEh1YjoKCiogW2BnZ1RpbWVTZXJpZXNgXShodHRwczovL2dpdGh1Yi5jb20vQXRoZXJFbmVyZ3kvZ2dUaW1lU2VyaWVzKQoqIFtgc3RyZWFtZ3JhcGhgXShodHRwczovL2hyYnJtc3RyLmdpdGh1Yi5pby9zdHJlYW1ncmFwaC8pICh1c2VzIEQzKQoqIFtgZ2dzdHJlYW1gXShodHRwczovL2dpdGh1Yi5jb20vZGF2aWRzam9iZXJnL2dnc3RyZWFtKS4KCkEgc3RyZWFtIGdyYXBoIGZvciBtb3ZpZSBnZW5yZXMgKHRoZXNlIGFyZSBub3QgbXV0dWFsbHkgZXhjbHVzaXZlKToKCmBgYHtyLCB3YXJuaW5nID0gRkFMU0UsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQojIyBpbnN0YWxsIHdpdGg6IHJlbW90ZXM6Omluc3RhbGxfZ2l0aHViKCJocmJybXN0ci9zdHJlYW1ncmFwaCIpCmxpYnJhcnkoc3RyZWFtZ3JhcGgpCmxpYnJhcnkodGlkeXZlcnNlKQpnZW5yZXMgPC0gYygiQWN0aW9uIiwgIkFuaW1hdGlvbiIsICJDb21lZHkiLAogICAgICAgICAgICAiRHJhbWEiLCAiRG9jdW1lbnRhcnkiLCAiUm9tYW5jZSIpCm15bW92aWVzIDwtIHNlbGVjdChnZ3Bsb3QybW92aWVzOjptb3ZpZXMsCiAgICAgICAgICAgICAgICAgICB5ZWFyLCBvbmVfb2YoZ2VucmVzKSkKbXltb3ZpZXNfbG9uZyA8LSBwaXZvdF9sb25nZXIoCiAgICBteW1vdmllcywgLXllYXIsCiAgICBuYW1lc190byA9ICJnZW5yZSIsCiAgICB2YWx1ZXNfdG8gPSAidmFsdWUiKQptb3ZpZV9jb3VudHMgPC0gY291bnQobXltb3ZpZXNfbG9uZywKICAgICAgICAgICAgICAgICAgICAgIHllYXIsIGdlbnJlKQpzdHJlYW1ncmFwaChtb3ZpZV9jb3VudHMsICJnZW5yZSIsICJuIiwgInllYXIiKQpgYGAKCjwhLS0KbmljZSBleGFtcGxlIHdpdGggWG1lbiBjaGFyYWN0ZXJzIGZyb20gVGlkeVR1ZXNkYXkKaHR0cHM6Ly9naXRodWIuY29tL1ozdHQvVGlkeVR1ZXNkYXkvYmxvYi9tYXN0ZXIvUi8yMDIwXzI3X0NsYXJlbW9udFJ1blhNZW4uUm1kCi0tPgoKCiMjIFJlYWRpbmcKCkNoYXB0ZXJzIFtfVmlzdWFsaXppbmcKICBwcm9wb3J0aW9uc19dKGh0dHBzOi8vY2xhdXN3aWxrZS5jb20vZGF0YXZpei92aXN1YWxpemluZy1wcm9wb3J0aW9ucy5odG1sKQogIGFuZCBbX1Zpc3VhbGl6aW5nIG5lc3RlZAogIHByb3BvcnRpb25zX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6L25lc3RlZC1wcm9wb3J0aW9ucy5odG1sKQogIGluIFtfRnVuZGFtZW50YWxzIG9mIERhdGEKICBWaXN1YWxpemF0aW9uX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6LykuCgoKIyMgSW50ZXJhY3RpdmUgVHV0b3JpYWwKCkFuIGludGVyYWN0aXZlIFtgbGVhcm5yYF0oaHR0cHM6Ly9yc3R1ZGlvLmdpdGh1Yi5pby9sZWFybnIvKSB0dXRvcmlhbApmb3IgdGhlc2Ugbm90ZXMgaXMgW2F2YWlsYWJsZV0oYHIgV0xOSygidHV0b3JpYWxzL3Byb3BvcnRpb25zLlJtZCIpYCkuCgpZb3UgY2FuIHJ1biB0aGUgdHV0b3JpYWwgd2l0aAoKYGBge3IsIGV2YWwgPSBGQUxTRX0KU1RBVDQ1ODA6OnJ1blR1dG9yaWFsKCJwcm9wb3J0aW9ucyIpCmBgYAoKWW91IGNhbiBpbnN0YWxsIHRoZSBjdXJyZW50IHZlcnNpb24gb2YgdGhlIGBTVEFUNDU4MGAgcGFja2FnZSB3aXRoCgpgYGB7ciwgZXZhbCA9IEZBTFNFfQpyZW1vdGVzOjppbnN0YWxsX2dpdGxhYigibHVrZS10aWVybmV5L1NUQVQ0NTgwIikKYGBgCgpZb3UgbWF5IG5lZWQgdG8gaW5zdGFsbCB0aGUgYHJlbW90ZXNgIHBhY2thZ2UgZnJvbSBDUkFOIGZpcnN0LgoKCiMjIEV4ZXJjaXNlcwoKMS4gRmlndXJlIEEgc2hvd3MgYSBiYXIgY2hhciBvZiB0aGUgZmxpZ2h0cyBsZWF2aW5nIE5ZQyBhaXJwb3J0cyBpbgogICAyMDEzIGZvciBlYWNoIGRheSBvZiB0aGUgd2Vlay4gRmlndXJlIEIgc2hvd3MgdGhlIG1hcmtldCBzaGFyZSBvZgogICBmaXZlIG1ham9yIGludGVybmV0IGJyb3dzZXJzIGluIDIwMTUuCgogICAgYGBge3IsIG1lc3NhZ2UgPSBGQUxTRSwgZWNobyA9IEZBTFNFLCBmaWcuaGVpZ2h0ID0gNCwgZmlnLndpZHRoID0gOH0KICAgIGxpYnJhcnkobHVicmlkYXRlKQogICAgbGlicmFyeShkcGx5cikKICAgIGxpYnJhcnkobnljZmxpZ2h0czEzKQogICAgbGlicmFyeShnZ3Bsb3QyKQogICAgbGlicmFyeShwYXRjaHdvcmspCiAgICB0aG0gPC0gdGhlbWVfbWluaW1hbCgpICsgdGhlbWUodGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gMTUpKQogICAgcDEgPC0gbXV0YXRlKGZsaWdodHMsCiAgICAgICAgICAgICAgICAgZGF0ZSA9IG1ha2VfZGF0ZSh5ZWFyLCBtb250aCwgZGF5KSwKICAgICAgICAgICAgICAgICB3ZGF5ID0gd2RheShkYXRlLCBsYWJlbCA9IFRSVUUsIGFiYnIgPSBUUlVFKSkgfD4KICAgICAgICBnZ3Bsb3QoYWVzKHggPSB3ZGF5KSkgKwogICAgICAgIGdlb21fYmFyKGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgICAgIHNjYWxlX3lfY29udGludW91cyhleHBhbmQgPSBjKDAsIDApKSArCiAgICAgICAgbGFicyh0aXRsZSA9ICJGbGlnaHRzIGZyb20gTllDIGluIDIwMTMiLAogICAgICAgICAgICAgc3VidGl0bGUgPSAiQnkgRGF5IG9mIHRoZSBXZWVrIiwKICAgICAgICAgICAgIGNhcHRpb24gPSAiRmlndXJlIEEiLAogICAgICAgICAgICAgeCA9IE5VTEwsCiAgICAgICAgICAgICB5ID0gIk51bWJlciBvZiBGbGlnaHRzIikgKwogICAgICAgIHRobQoKICAgIGJyb3dzZXJzMjAxNSA8LQogICAgICAgIGRhdGEuZnJhbWUoQnJvd3NlciA9IGMoIk9wZXJhIiwgIlNhZmFyaSIsICJGaXJlZm94IiwgIkNocm9tZSIsICJJRSIpLAogICAgICAgICAgICAgICAgICAgc2hhcmUgPSBjKDIsIDIyLCAyMSwgMjcsIDI5KSkKICAgIHAyIDwtIGdncGxvdChicm93c2VyczIwMTUsIGFlcyh4ID0gQnJvd3NlciwgeSA9IHNoYXJlKSkgKwogICAgICAgIGdlb21fY29sKGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgICAgIHNjYWxlX3lfY29udGludW91cyhleHBhbmQgPSBjKDAsIDApKSArCiAgICAgICAgbGFicyh0aXRsZSA9ICJCcm93c2VyIE1hcmtldCBTaGFyZSIsCiAgICAgICAgICAgICBzdWJ0aXRsZSA9ICIyMDE1IiwKICAgICAgICAgICAgIGNhcHRpb24gPSAiRmlndXJlIEIiLAogICAgICAgICAgICAgeCA9IE5VTEwsCiAgICAgICAgICAgICB5ID0gIlBlcmNlbnQiKSArCiAgICAgICAgdGhtCgogICAgcDEgfCBwMgogICAgYGBgCgogICAgRm9yIHdoaWNoIG9mIHRoZXNlIGJhciBjaGFydHMgd291bGQgaXQgYmUgYmV0dGVyIHRvIHJlb3JkZXIgdGhlCiAgICBjYXRlZ29yaWVzIHNvIHRoZSBiYXJzIGFyZSBvcmRlcmVkIGZyb20gbGFyZ2VzdCB0byBzbWFsbGVzdD8KICAgIAogICAgYS4gWWVzIGZvciBGaWd1cmUgQS4gTm8gZm9yIEZpZ3VyZSBCLgogICAgYi4gTm8gZm9yIEZpZ3VyZSBBLiBZZXMgZm9yIEZpZ3VyZSBCLgogICAgYy4gWWVzIGZvciBib3RoLgogICAgZC4gTm8gZm9yIGJvdGguCgoyLiAgQ29uc2lkZXIgdGhlIHN0YWNrZWQgYmFyIGNoYXJ0IGBwMWAgYW5kIHRoZSBzcGluZSBwbG90IGBwMmAgZm9yCiAgICB0aGUgaGFpciBhbmQgZXllIGNvbG9yIGRhdGEgcHJvZHVjZWQgYnkgdGhlIGZvbGxvd2luZyBjb2RlOgoKICAgIGBgYHtyLCBldmFsID0gRkFMU0V9CiAgICBsaWJyYXJ5KGRwbHlyKQogICAgbGlicmFyeShnZ3Bsb3QyKQogICAgbGlicmFyeShnZ21vc2FpYykKICAgIGVjb2xzIDwtIGMoQnJvd24gPSAiYnJvd240IiwgQmx1ZSA9ICJibHVlMiIsCiAgICAgICAgICAgICAgIEhhemVsID0gImRhcmtnb2xkZW5yb2QzIiwgR3JlZW4gPSAiZ3JlZW40IikKICAgIEhhaXJFeWVDb2xvckRGIDwtIGFzLmRhdGEuZnJhbWUoSGFpckV5ZUNvbG9yKQogICAgcDAgPC0gZ2dwbG90KEhhaXJFeWVDb2xvckRGKSArCiAgICAgICAgc2NhbGVfZmlsbF9tYW51YWwodmFsdWVzID0gZWNvbHMpICsKICAgICAgICB0aGVtZV9taW5pbWFsKCkKCiAgICBwMSA8LSBwMCArIGdlb21fY29sKGFlcyh4ID0gSGFpciwgeSA9IEZyZXEgLyBzdW0oRnJlcSksIGZpbGwgPSBFeWUpKQoKICAgIHAyIDwtIHAwICsgZ2VvbV9tb3NhaWMoYWVzKHggPSBwcm9kdWN0KEhhaXIpLCBmaWxsID0gRXllLCB3ZWlnaHQgPSBGcmVxKSkKICAgIGBgYAoKICAgIFVzZSB0aGUgdHdvIHBsb3RzIHRvIGFuc3dlcjogV2hpY2ggaGFpciBjb2xvciBoYXMgdGhlIGhpZ2hlc3QKICAgIHByb3BvcnRpb24gb2YgaW5kaXZpZHVhbHMgd2l0aCBncmVlbiBleWVzPwoKICAgIGEuIEJsYWNrCiAgICBiLiBCcm93bgogICAgYy4gUmVkCiAgICBkLiBCbG9uZAoKICAgIFdoaWNoIHBsb3QgbWFrZXMgaXQgZWFzaWVzdCB0byBhbnN3ZXIgdGhpcyBxdWVzdGlvbj8KCjMuICBVc2UgdGhlIHBsb3RzIG9mIHRoZSBwcmV2aW91cyBxdWVzdGlvbiB0byBhbnN3ZXI6IFRoZSBwcm9wb3J0aW9uCiAgICBvZiBpbmRpdmlkdWFscyB3aXRoIHJlZCBoYWlyIGlzIGNsb3Nlc3QgdG86CgogICAgYS4gNSUKICAgIGIuIDglCiAgICBjLiAxMiUKICAgIGQuIDIwJQoKICAgIFdoaWNoIHBsb3QgbWFrZXMgaXQgZWFzaWVzdCB0byBhbnN3ZXIgdGhpcyBxdWVzdGlvbj8KCjwhLS0KcGFyZXRvIGNoYXJ0CgogIC0gcGllIGNoYXJ0cwogIC0gYmFyIGNoYXJ0cwogIC0gc3RhY2tlZCBiYXIgY2hhcnRzCiAgLSBncm91cGVkIGJhciBjaGFydHMKICAtIHBvcHVsYXRpb24gcHlyYW1pZHMKICAtIHdhZmZsZSBjaGFydHMsIHNxdWFyZSBwaWUgY2hhcnRzCgogIC0gam9pbnQgYW5kIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMKICAtIHNwaW5lIHBsb3RzCiAgLSBzcGlub2dyYW1zPwogIC0gZG91YmxlIGRlY2tlciBwbG90cwogIC0gY2RfcGxvdHMKICAtIG1vc2FpYyBwbG90cwogIC0gdHJlZSBtYXBzCiAgLSBzYW5rZXkgZGlhZ3JhbXMsIGFsbHV2aWFsIGNoYXJ0cywgcGFyYWxsZWwgc2V0cwogIC0gY2hvcmQgZGlhZ3JhbXMKICAtIHN0cmVhbSBncmFwaHMKLS0+Cg==
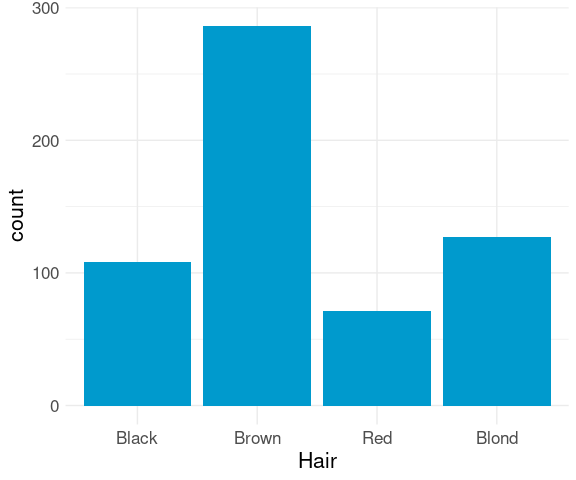


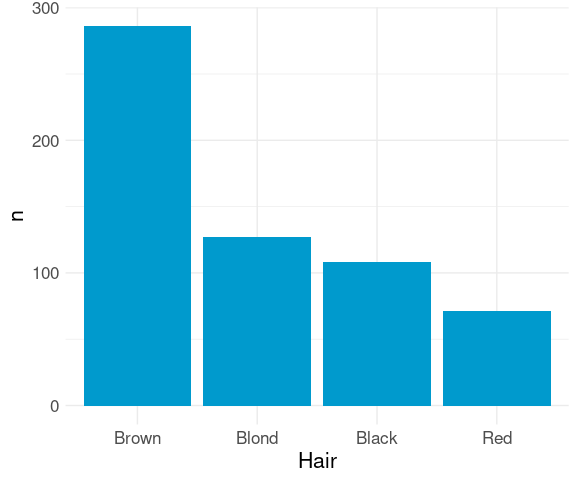
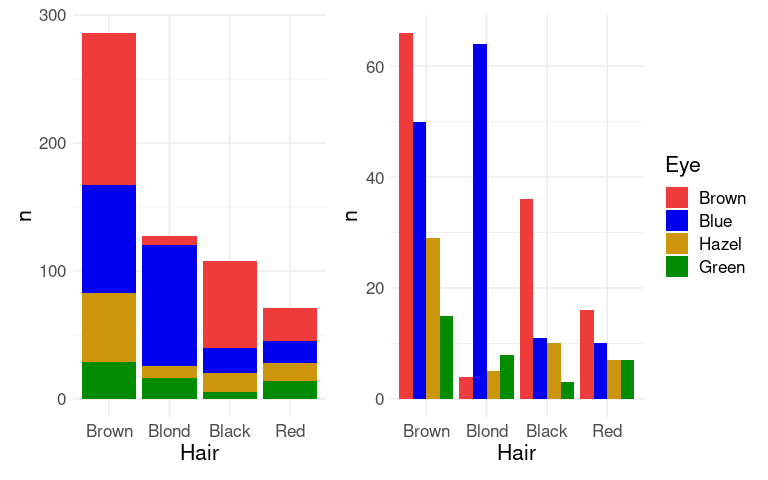
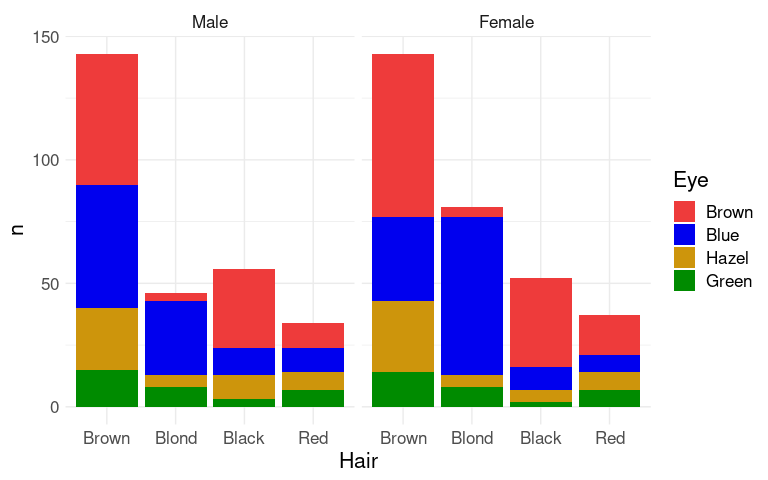

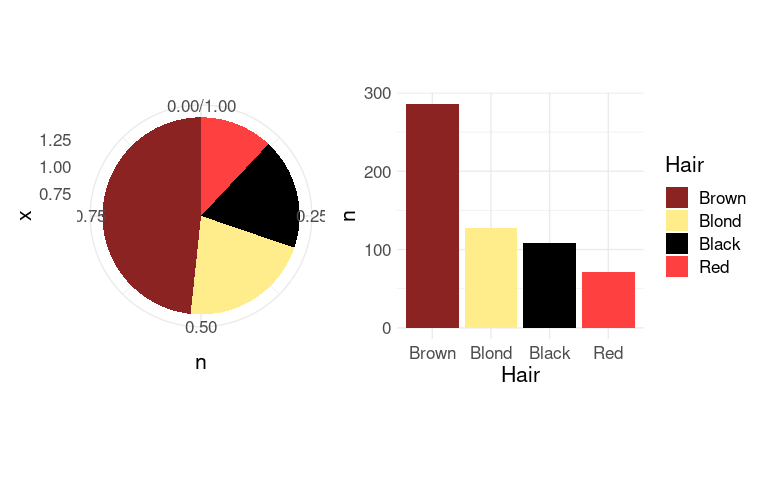
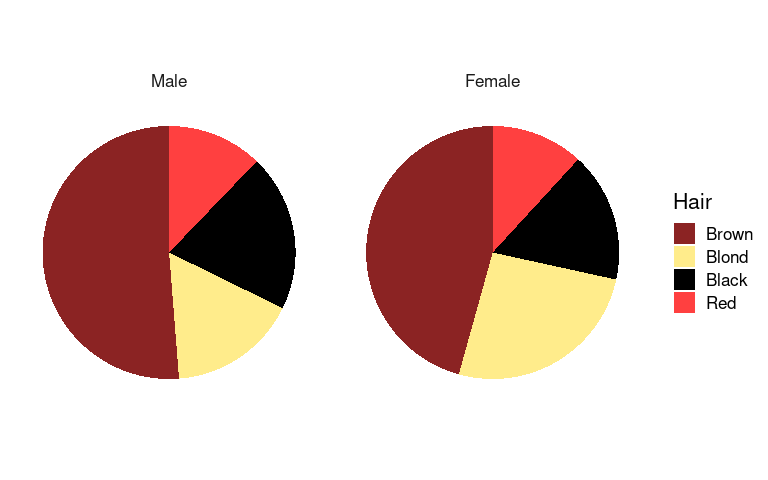
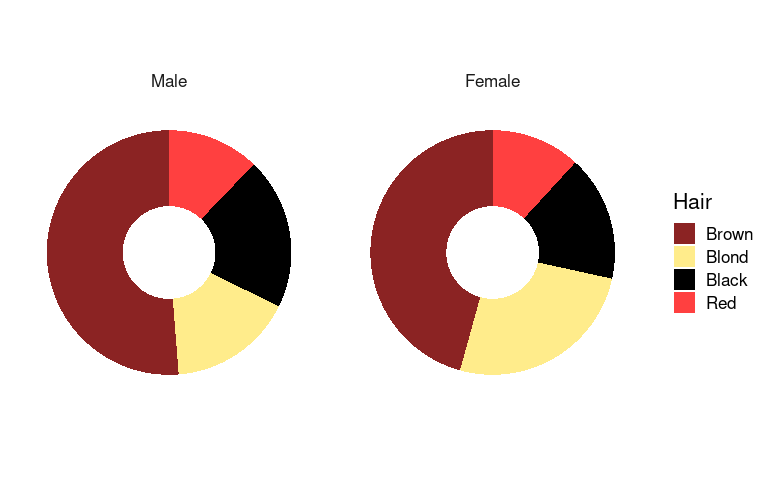
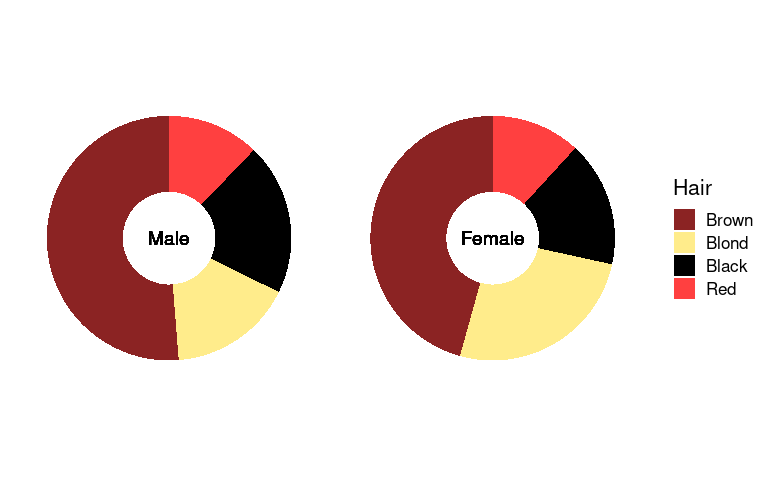
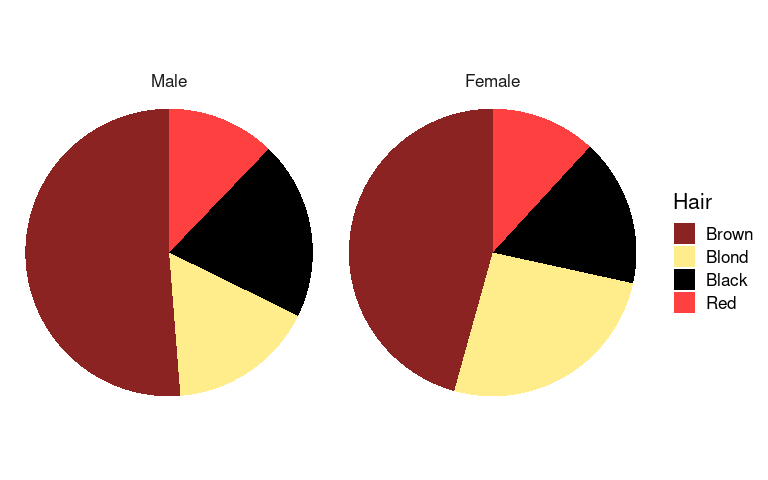
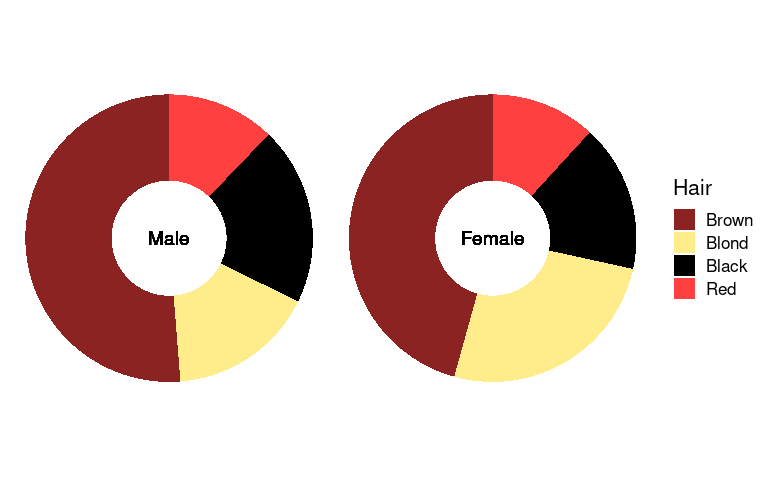

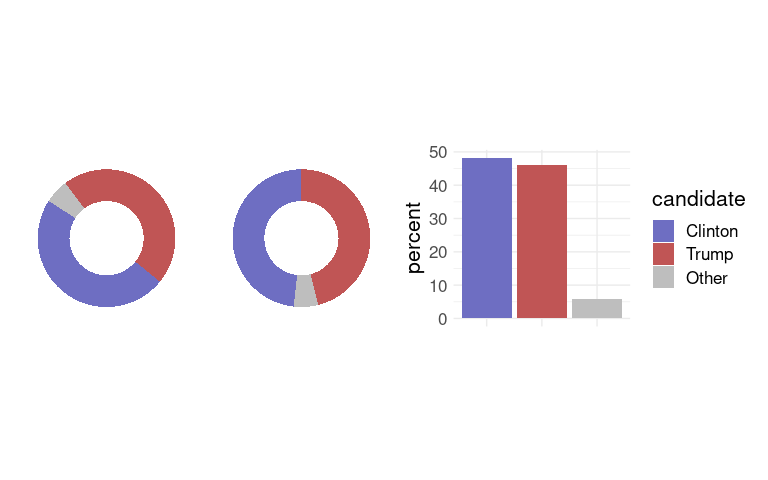
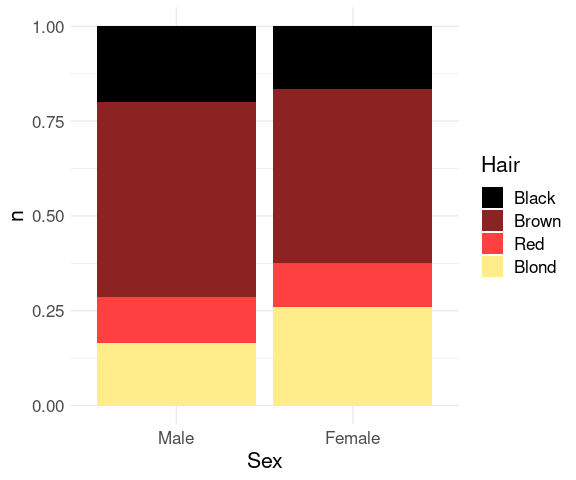
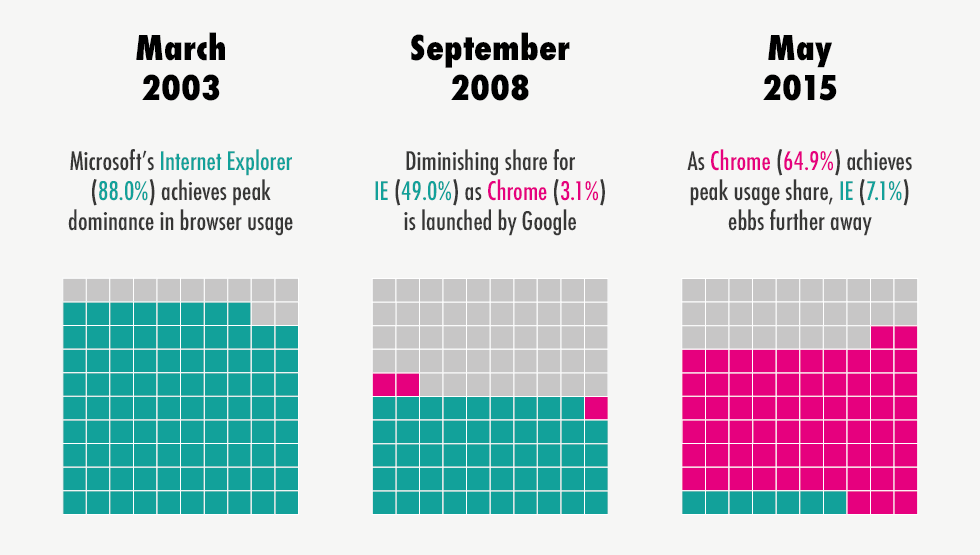

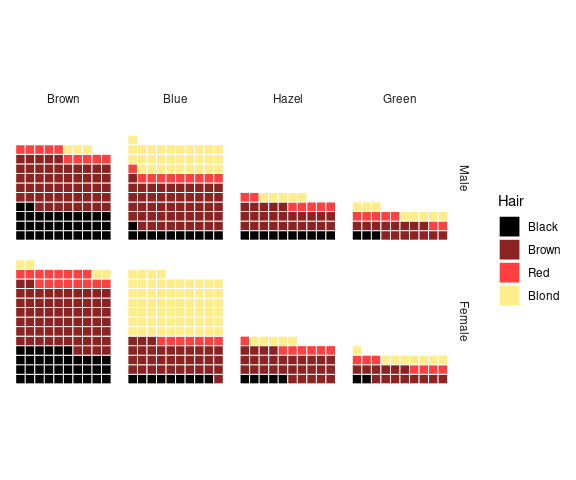
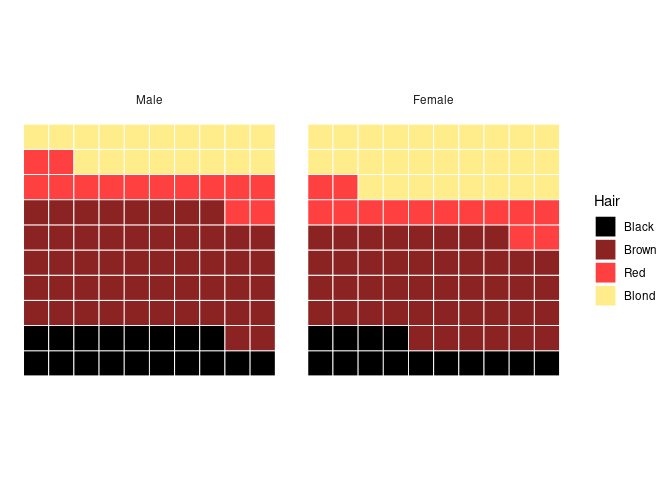
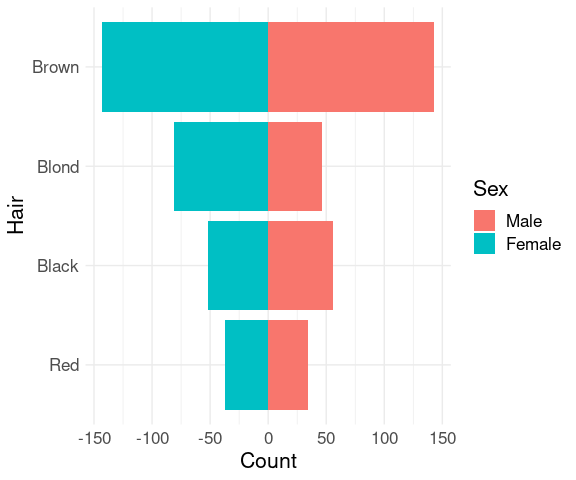


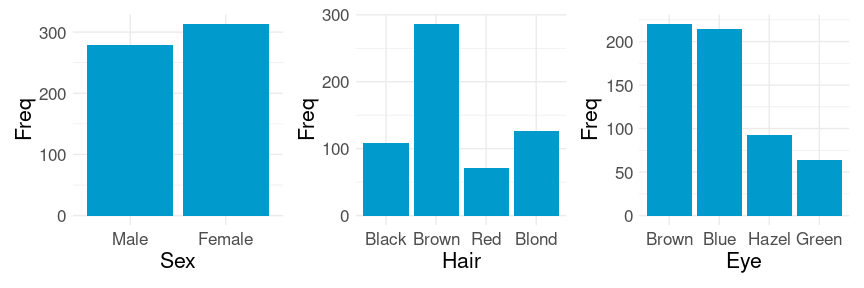

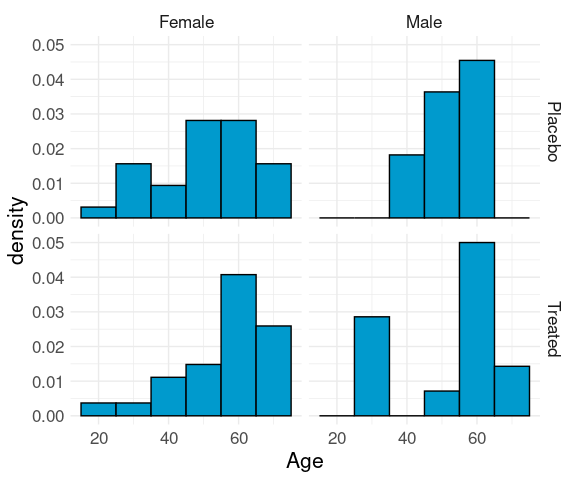
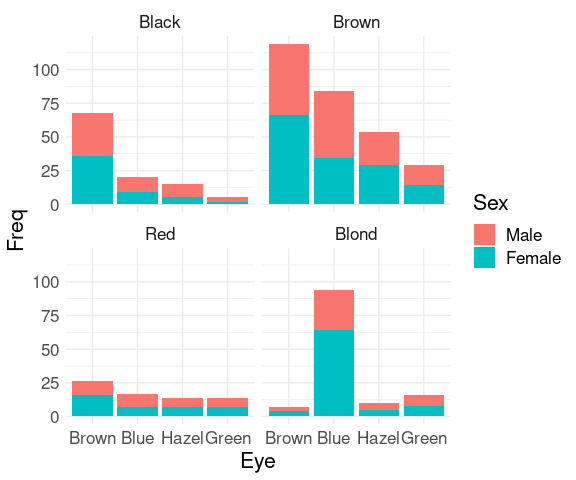
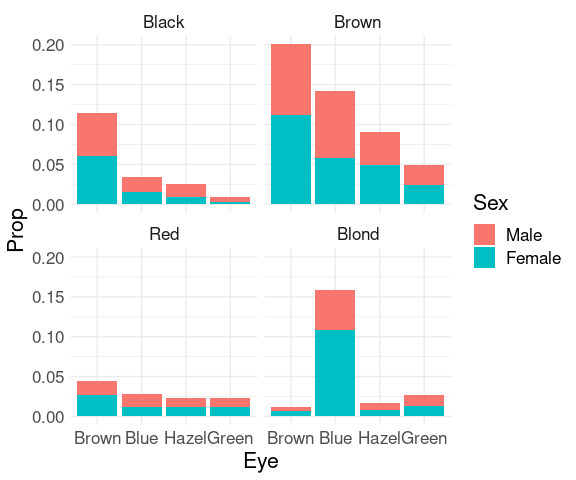
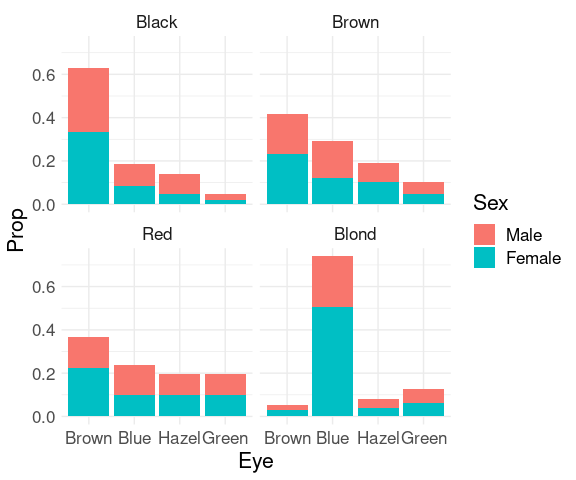

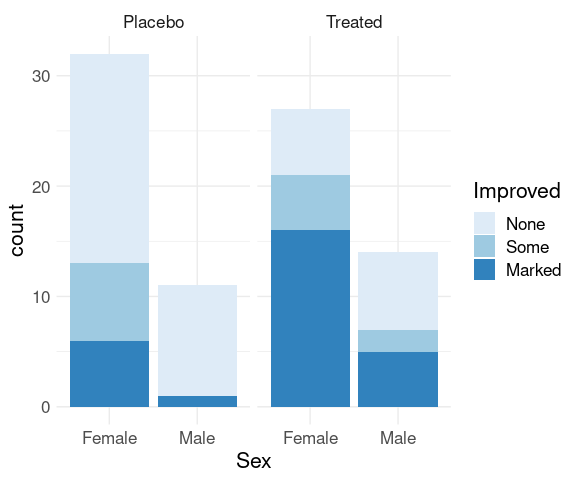
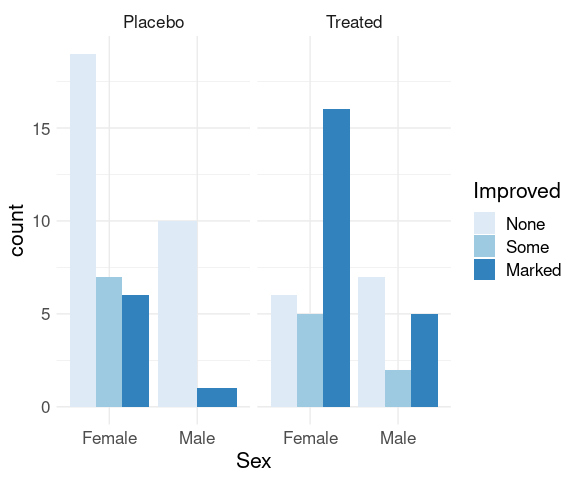
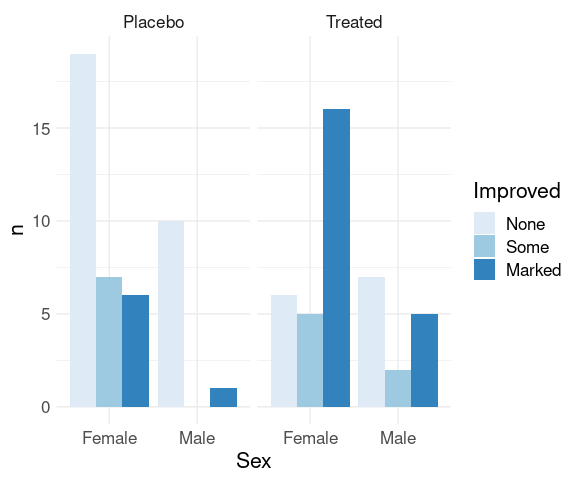
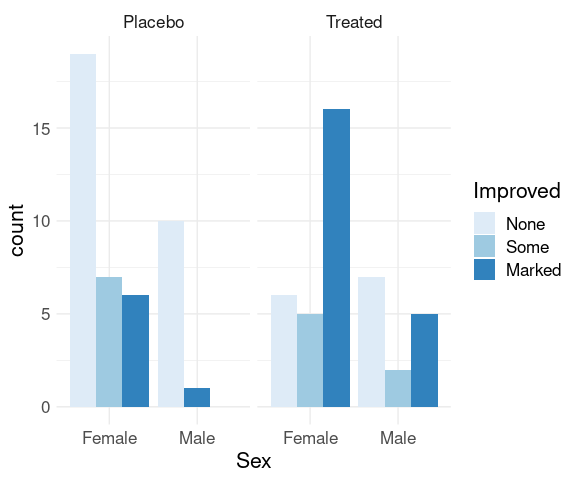
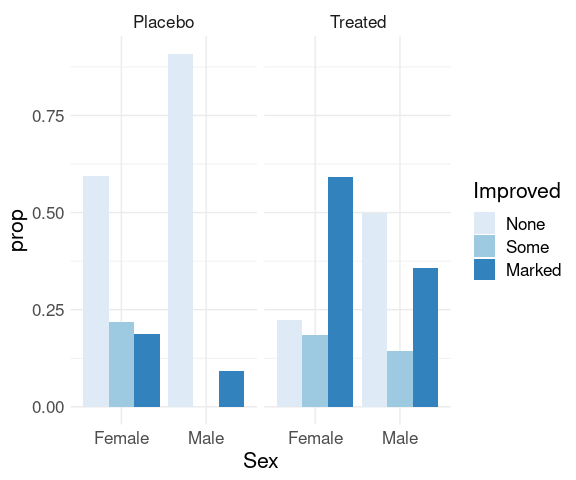
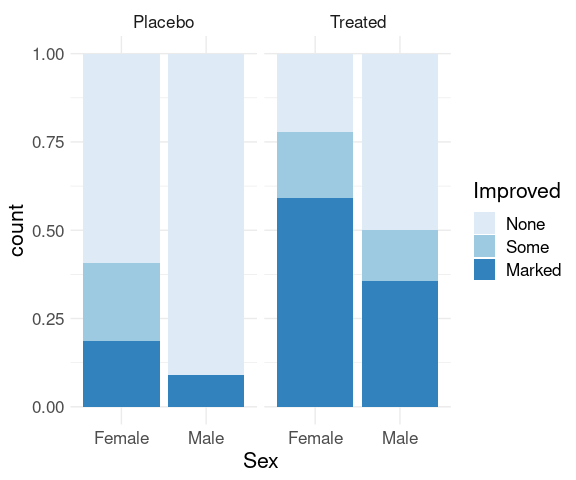
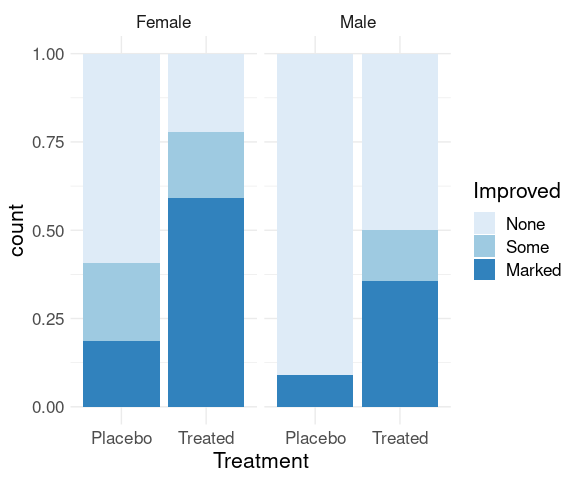
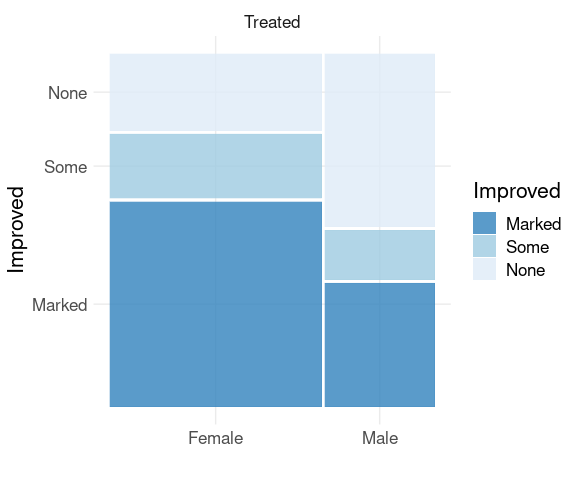
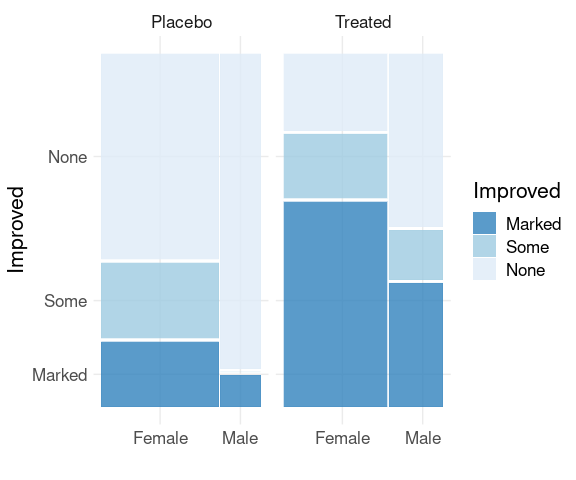
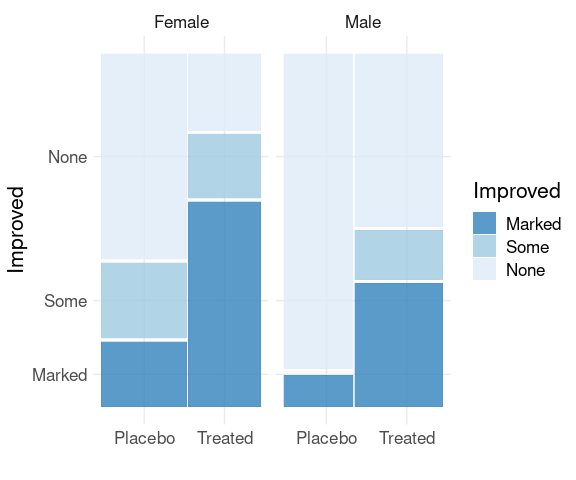 This no longer shows the Female/Male imbalance.
This no longer shows the Female/Male imbalance.