Introduction
Once there are more than a handful of numeric data values it is often useful to step back and look at the distribution of the data values:
Where is the bulk of the data located?
Is there a single area of concentration or are there several?
Is the data distribution symmetric or is it skewed, i.e. trails off more slowly in one direction or another?
Are there extreme, or outlying, values?
Are there any suspicious or impossible values?
Are there gaps in the data?
Is there rounding, e.g. to integer values, or heaping , i.e. a few particular values occur very frequently?
Plots for visualizing distributions include
Strip plots.
Histograms.
Density plots.
Box plots.
Violin plots.
Swarm plots.
Density ridges
Strip Plots
Strip Plot Basics
A variant of the dot plot is known as a strip plot .
A strip plot for the city temperature data is
thm <- theme_minimal() +
theme(text = element_text(size = 16))
ggplot(citytemps) +
geom_point(aes(x = temp, y = "All")) +
thm +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank())
The strip plot can reveal gaps and outliers.
After looking at the plot we might want to examine the high and low values:
filter(citytemps, temp > 85)
## city temp
## 1 Asuncion 99
## 2 Dar es Salaam 92
## 3 Kingston 87
## 4 Kinshasa 89
## 5 Managua 90
## 6 Santiago 88
## 7 Santo Domingo 88
filter(citytemps, temp < 10)
## city temp
## 1 Almaty 9
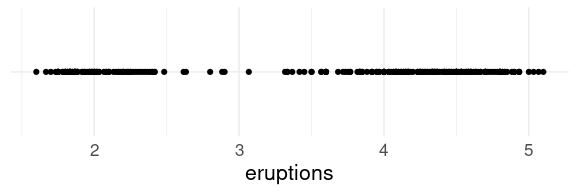
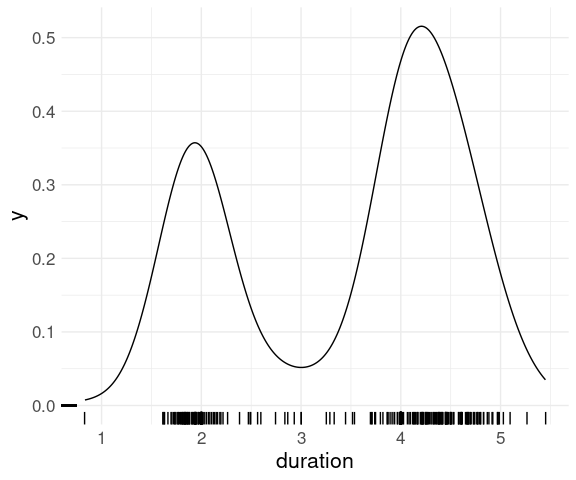
## 2 Anadyr -23For the eruption durations in the faithful data a strip plot shows the two modes around 2 and 4 minutes:
ggplot(faithful) +
geom_point(aes(x = eruptions, y = "All")) +
thm +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank())
Multiple Groups
Strip plots are most useful for showing subsets corresponding to a categorical variable.
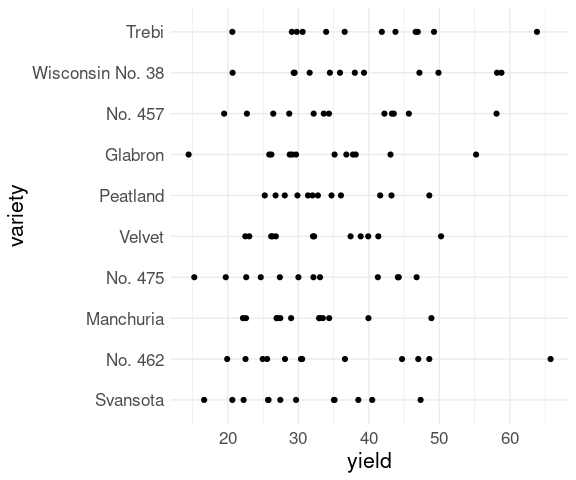
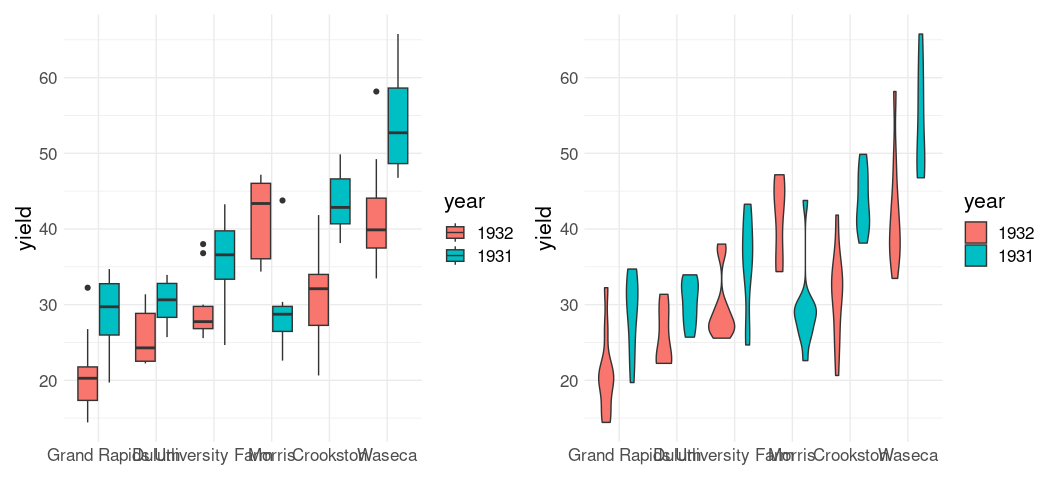
A strip plot for the yields for different varieties in the barley data is
ggplot(barley) +
geom_point(aes(x = yield, y = variety)) +
theme_minimal() +
thm
Scalability
Scalability in this form is limited due to over-plotting.
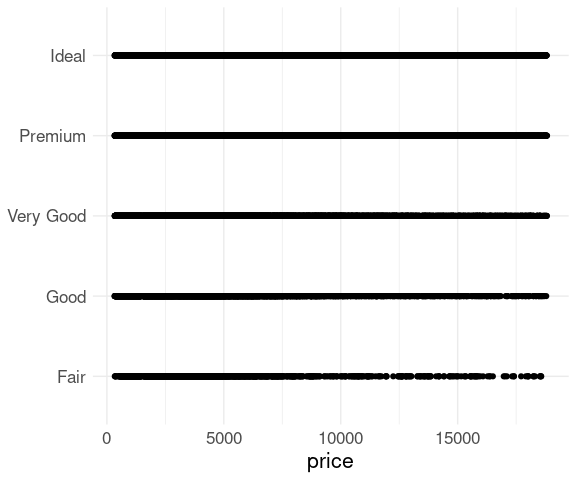
A simple strip plot of price within the different cut levels in the diamonds data is not very helpful:
ggplot(diamonds) +
geom_point(aes(x = price, y = cut)) +
thm +
theme(axis.title.y = element_blank())
Several approaches are available to reduce the impact of over-plotting:
reduce the point size;
random displacement of points, called jittering ;
making the points translucent, or alpha blending .
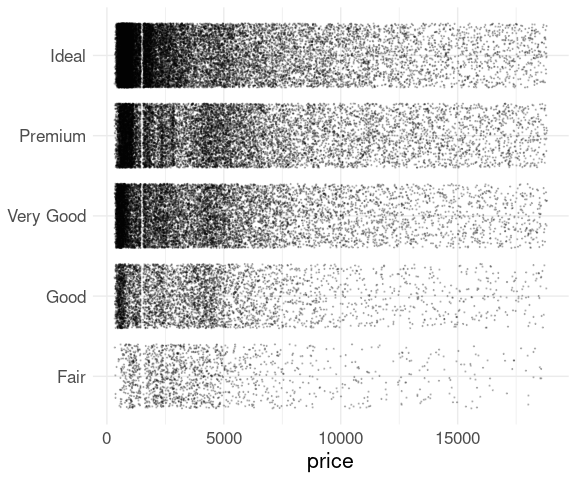
Combining all three for examining price within cut for the diamonds data produces
ggplot(diamonds) +
geom_point(aes(x = price, y = cut),
size = 0.2,
position = position_jitter(width = 0),
alpha = 0.2) +
thm + theme(axis.title.y = element_blank())
Skewness of the price distributions can be seen in this plot, though other approaches will show this more clearly.
A peculiar feature reveled by this plot is the gap below 2000.
Examining the subset with price < 2000 shows the gap is roughly symmetric around 1500:
ggplot(filter(diamonds, price < 2000)) +
geom_point(aes(x = price, y = cut),
size = 0.2,
position = position_jitter(width = 0),
alpha = 0.2) +
thm +
theme(axis.title.y = element_blank())
A plot along these lines was used on the New York Times front page for February 21, 2021 .
Some Notes
With a good combination of point size choice, jittering, and alpha blending the strip plot for groups of data can scale to several hundred thousand observations and ten to twenty of groups.
For very large datat sets it can be useful to look at a strip plot of a sample of the data.
Strip plots can reveal gaps, outliers, and data outside of the expected range.
Skewness and multi-modality can be seen, but other visualizations show these more clearly.
Storage needed for vector graphics images grows linearly with the number of observations.
Base graphics provides stripchart and lattice provides stripplot.
Histograms
Histogram Basics
Historams are constructed by binning the data and counting the number of observations in each bin.
The objective is usually to visualize the shape of the distribution.
The number of bins needs to be
A very small bin width can be used to look for rounding or heaping.
Common choices for the vertical scale are:
bin counts, or frequencies;
counts per unit, or densities.
The count scale is more intepretable for lay viewers.
The density scale is more suited for comparison to mathematical density models.
Constructing histograms with unequal bin widths is possible but rarely a good idea.
Histograms in R
There are many ways to plot histograms in R:
the hist() function in the base graphics package;
truehist() in package MASS;
histogram() in package lattice;
geom_histogram() in package ggplot2.
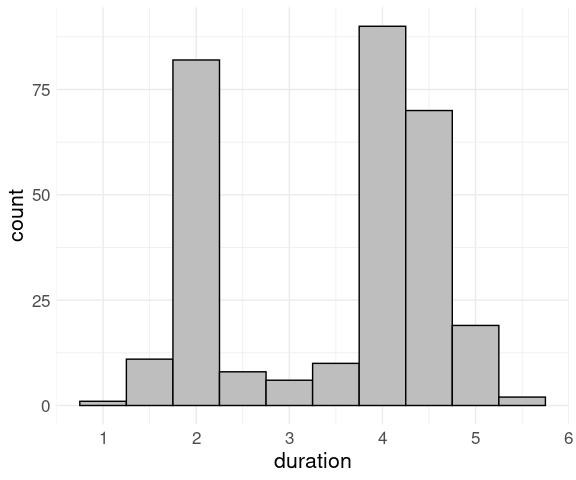
A histogram of eruption durations for another data set on Old Faithful eruptions, this one from package MASS:
data(geyser, package = "MASS")
ggplot(geyser) +
geom_histogram(aes(x = duration)) +
thm
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
The default settings using geom_histogram are less than ideal.
Using a binwidth of 0.5 and customized fill and color settings produces a better result:
ggplot(geyser) +
geom_histogram(aes(x = duration),
binwidth = 0.5,
fill = "grey",
color = "black") +
thm
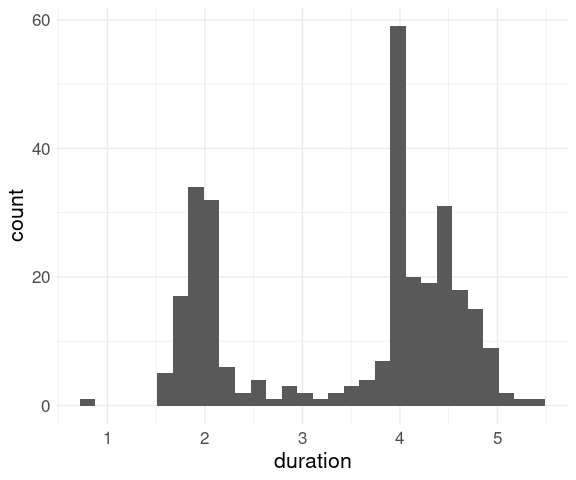
Reducing the bin width shows an interesting feature:
ggplot(geyser) +
geom_histogram(aes(x = duration),
binwidth = 0.05,
fill = "grey",
color = "black") +
thm
Eruptions were sometimes classified as short or long ; these were coded as 2 and 4 minutes.
For many purposes this kind of heaping or rounding does not matter.
It would matter if we wanted to estimate means and standard deviations of the durations of the long and short eruptions.
More data and information about geysers is available at https://geysertimes.org/ .
For exploration there is no one “correct” bin width or number of bins.
It would be very useful to be able to change this parameter interactively.
Superimposing a Density
A histogram can be used to compare the data distribution to a theoretical model, such as a normal distribution.
This requires using a density scale for the vertical axis.
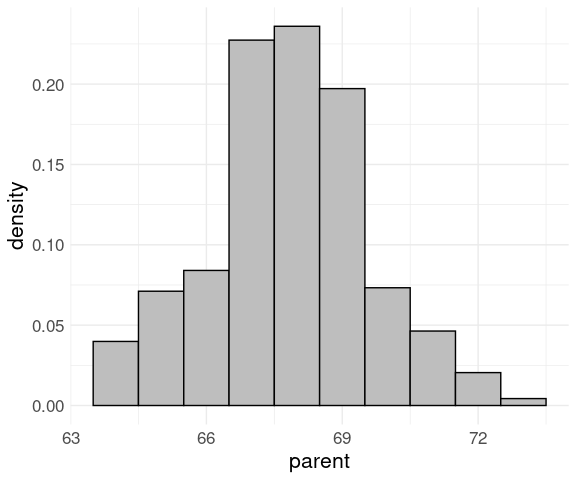
The Galton data frame in the HistData package is one of several data sets used by Galton to study the heights of parents and their children.
Adding a normal density curve to a ggplot histogram involves:
computing the parameters of the density;
creating the histogram with a density scale using the computed variable after_stat(density);
adding the function curve using geom_function, stat_function, or geom_line.
Create the histogram with a density scale using the computed varlable after_stat(density):
data(Galton, package = "HistData")
ggplot(Galton) +
geom_histogram(aes(x = parent,
y = after_stat(density)),
binwidth = 1,
fill = "grey",
color = "black") +
thm
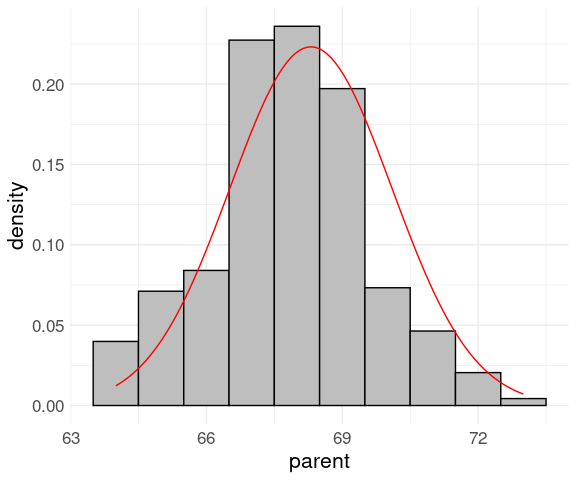
Then compute the mean and standard deviation and add the normal density curve:
data(Galton, package = "HistData")
p_mean <- mean(Galton$parent)
p_sd <- sd(Galton$parent)
p_dens <- function(x) dnorm(x, p_mean, p_sd)
ggplot(Galton) +
geom_histogram(aes(x = parent,
y = after_stat(density)),
binwidth = 1,
fill = "grey",
color = "black") +
geom_function(fun = p_dens, color = "red") +
thm
Multiple Groups
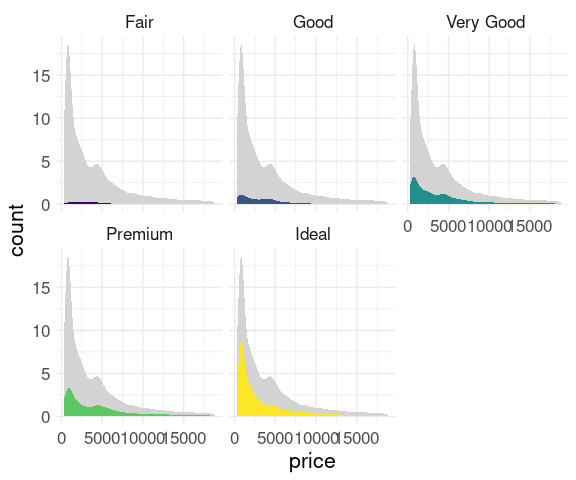
Faceting works well for showing comparative histograms for multiple groups.
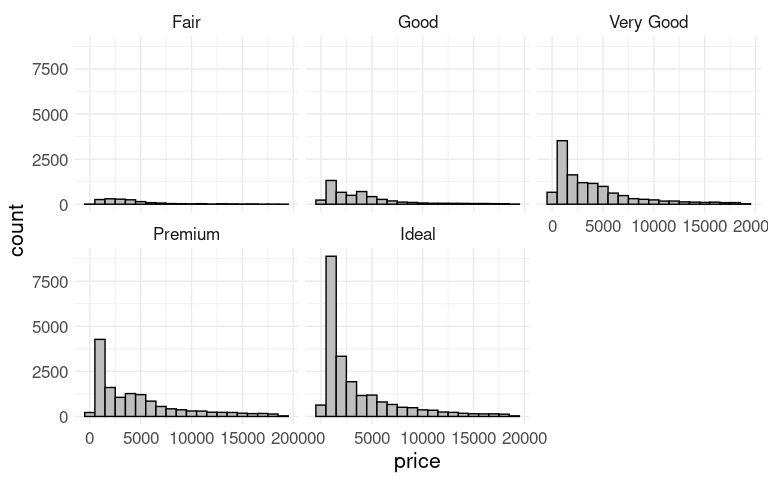
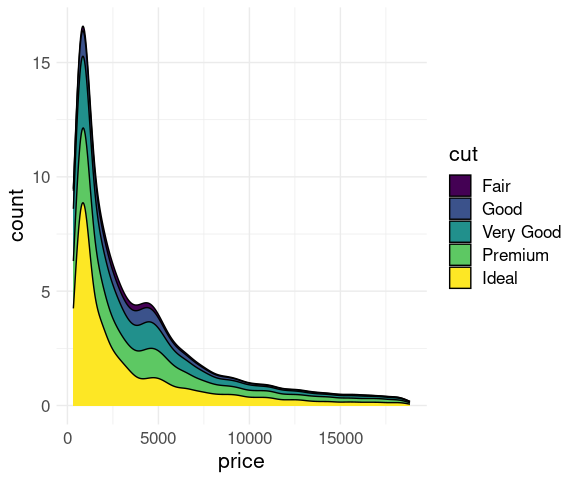
Histograms of price within cut for the diamonds data:
ggplot(diamonds) +
geom_histogram(aes(x = price),
binwidth = 1000,
color = "black", fill = "grey") +
facet_wrap(~ cut) +
thm
These histograms show counts on the vertical axis, and their sizes reflect the total counts for the groups.
Together the plots represent a view of the joint distribution of cut and price.
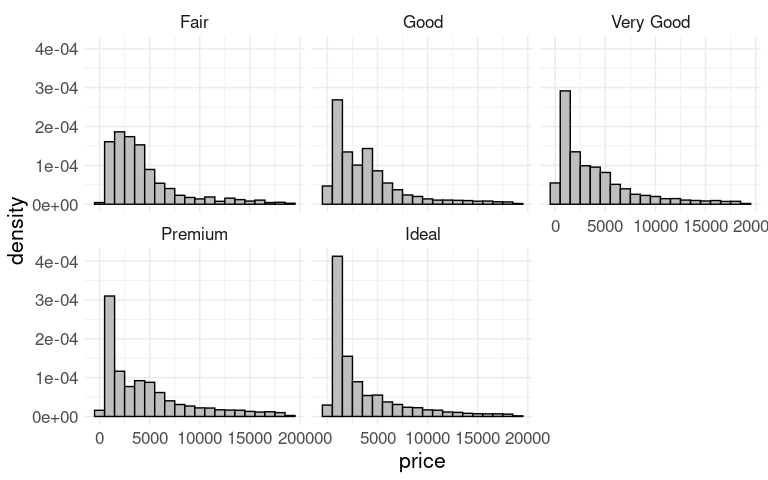
Switching to a density scale by using after_stat(density) for the y aesthetic allows the conditional distributions of price within groups to be compared:
p <- ggplot(diamonds) +
geom_histogram(aes(x = price,
y = after_stat(density)),
binwidth = 1000,
color = "black",
fill = "grey") +
thm
p + facet_wrap(~ cut)
By mapping the fill aesthetic to cut it is possible to produce a stacked histogram or a superimposed histogram
position = "stack", the default, for stacked;position = "identity" for superimposed.
But neither works very well visually.
For comparing locations of features it can help to facet with a single column.
But this may create aspect ratios that are not ideal.
Scalability
Histograms scale very well.
The visual performance does not deteriorate with increasing numbers of observations.
The computational effort needed is linear in the number of observations.
The amount of storage needed for an image object is linear in the number of bins.
Density Plots
Density Plot Basics
Density plots can be thought of as plots of smoothed histograms.
The smoothness is controlled by a bandwidth parameter that is analogous to the histogram binwidth.
Most density plots use a kernel density estimate
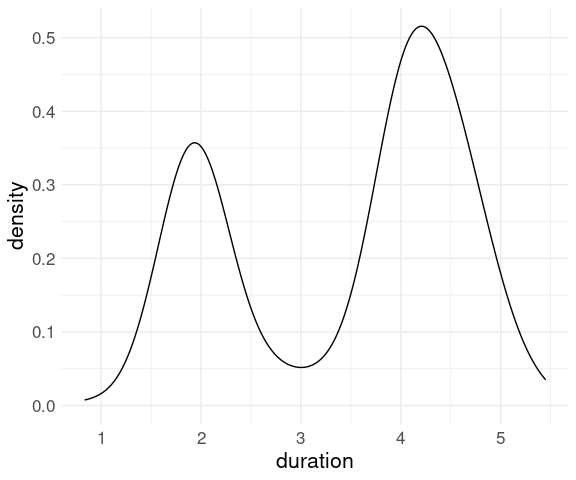
A density plot of the geyser duration variable with default bandwidth:
ggplot(geyser) +
geom_density(aes(x = duration)) +
thm
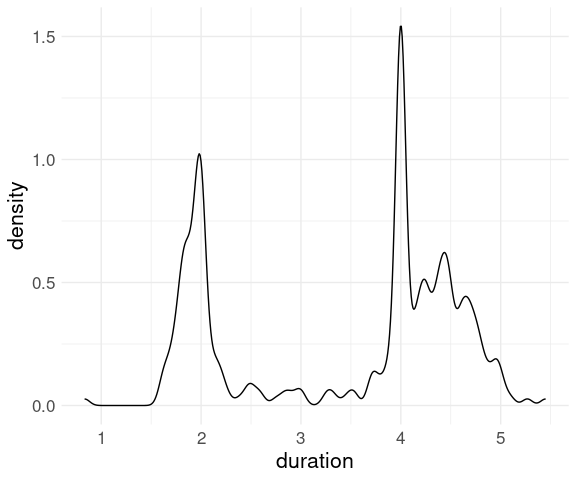
Using a smaller bandwidth shows the heaping at 2 and 4 minutes:
ggplot(geyser) +
geom_density(aes(x = duration), bw = 0.05) +
thm
For a moderate number of observations a useful addition is a jittered rug plot :
ggplot(geyser) +
geom_density(aes(x = duration)) +
geom_rug(aes(x = duration, y = 0),
position =
position_jitter(height = 0)) +
thm
Scalability
Visual scalability is very good.
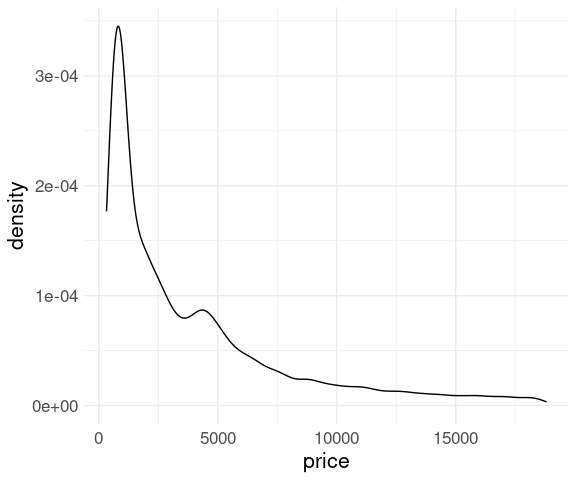
For the diamonds data price variable:
ggplot(diamonds) +
geom_density(aes(x = price)) +
thm
Density estimates are generally computed at a grid of points and interpolated.
Defaults in R vary from 50 to 512 points.
Computational effort for a density estimate at a point is proportional to the number of observations.
Storage needed for an image is proportional to the number of points where the density is estimated.
Multiple Groups
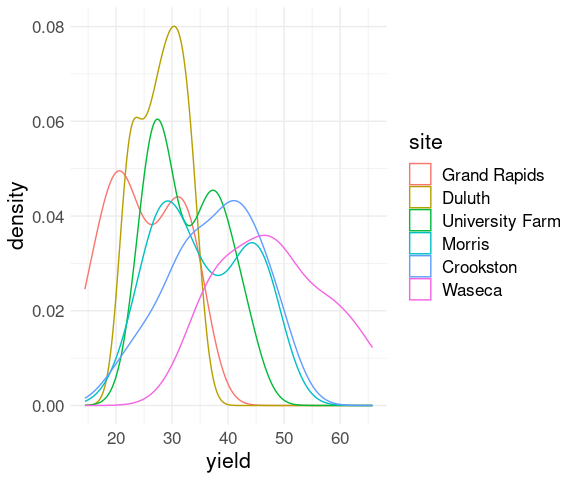
Density estimates for several groups can be shown in a single plot by mapping a group index to an aesthetic, such as color:
ggplot(barley) +
geom_density(aes(x = yield,
color = site)) +
thm
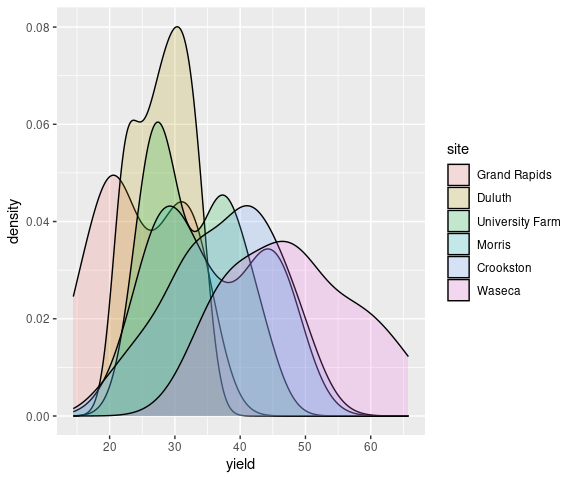
Using fill and alpha can also be useful:
ggplot(barley) +
geom_density(aes(x = yield,
fill = site),
alpha = 0.2)
Multiple densities in a single plot works best with a smaller number of categories, say 2 or 3:
ggplot(barley) +
geom_density(aes(x = yield,
fill = year),
alpha = 0.4) +
thm
Using small multiples, or faceting, may be a better option:
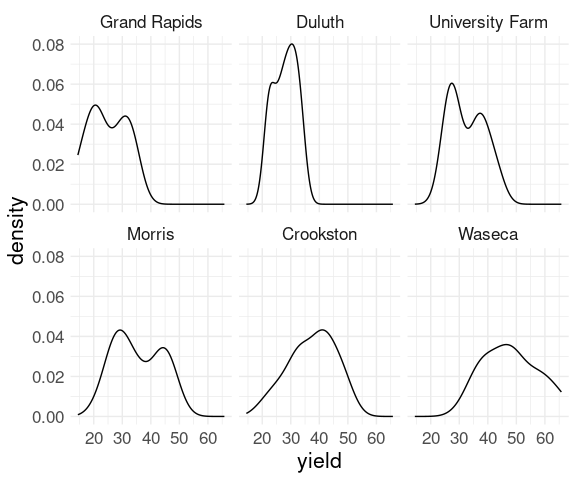
ggplot(barley) + geom_density(aes(x = yield)) + facet_wrap(~ site) + thm
These ideas can be combined:
ggplot(barley) +
geom_density(aes(x = yield, color = year)) +
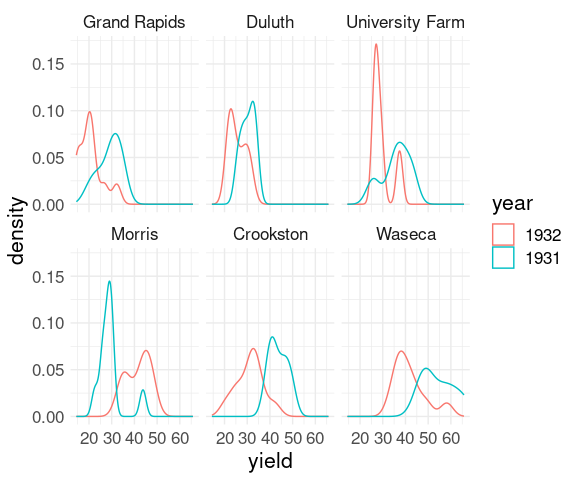
facet_wrap(~ site) +
thm
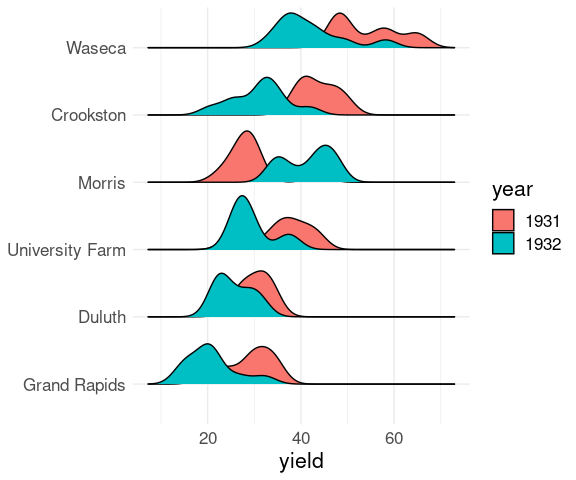
These plots again show lower yields for 1932 than for 1931 for all sites except Morris.
Density plots default to using the density scale.
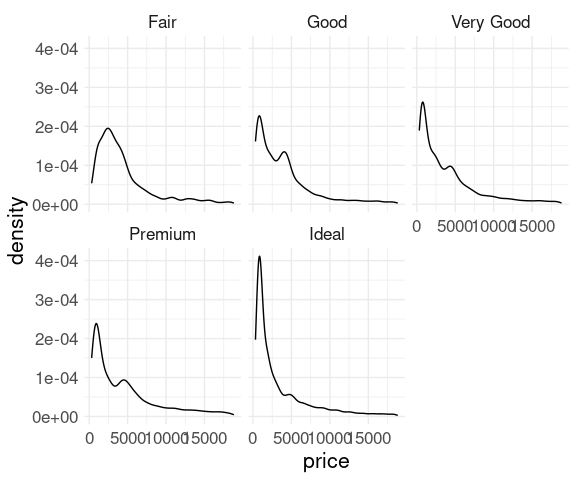
For the diamonds data a density plot of price faceted on cut shows the conditional distributions of price at the different cut levels:
ggplot(diamonds) +
geom_density(aes(x = price)) +
facet_wrap(~ cut) + thm
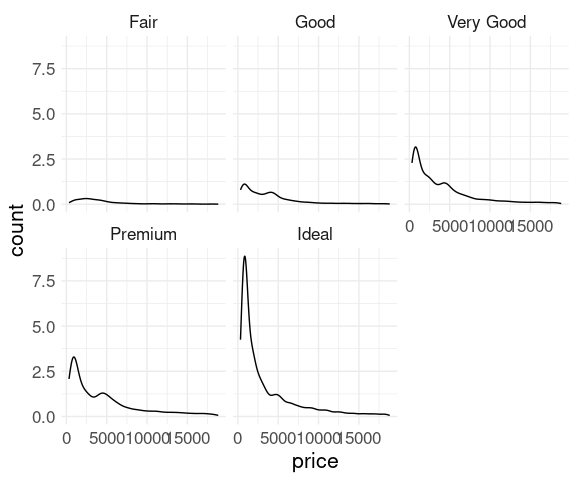
Mapping the y aesthetic to after_stat(count) shows the joint distribution of price and cut:
ggplot(diamonds) +
geom_density(aes(x = price,
y = after_stat(count))) +
facet_wrap(~ cut) + thm
A stacked density plot is sometimes useful but often hard to read:
ggplot(diamonds) +
geom_density(aes(x = price,
y = after_stat(count),
fill = cut),
position = "stack") +
thm
An intermediate option: A faceted plot on the count scale with a muted plot for the full data to allow proportions of the whole to be assessed:
ggplot(diamonds) +
geom_density(aes(x = price, y = after_stat(count)),
fill = "lightgrey", color = NA,
data = mutate(diamonds, cut = NULL)) +
geom_density(aes(x = price,
y = after_stat(count),
fill = cut),
position = "stack", color = NA) +
facet_wrap(~ cut) +
scale_fill_viridis_d(guide = "none") +
thm
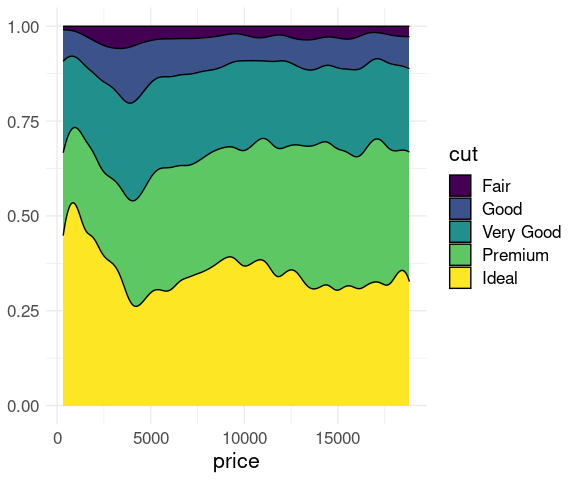
A filled density plot provides a vew of the conditional distribution of cut at the different price levels:
ggplot(diamonds) +
geom_density(aes(x = price, y = after_stat(count), fill = cut),
position = "fill") +
ylab(NULL) +
thm
This is called a CD plot , or a conditional density plot .
Some Notes
Computations are generally done with the base R function density.
plot has a method for the results returned by this function, so a density plot can be created with
plot(density(geyser$duration))The lattice package provides the function densityplot.
Interactive Bandwidth Choice
Being able to chose the bandwidth of a density plot, or the binwidth of a histogram, interactively is useful for exploration.
One way to do this in R (which unfortunately does not work on the RStudio server):
data(geyser, package = "MASS")
source("https://stat.uiowa.edu/~luke/classes/STAT7400/examples/tkdens.R")
tkdens(geyser$duration, tkrplot = TRUE)Another option:
data(geyser, package = "MASS")
source("https://stat.uiowa.edu/~luke/classes/STAT7400/examples/shinydens.R")
shinyDens(geyser$duration)
Boxplots
Boxplots , or box-and-whisker plots, provide a skeletal representation of a distribution.
They are very well suited for showing distributions for multiple groups.
There are many variations of boxplots:
Most start with a box from the first to the third quartiles and divided by the median.
The simplest form then adds a whisker from the lower quartile to the minimum and from the upper quartile to the maximum.
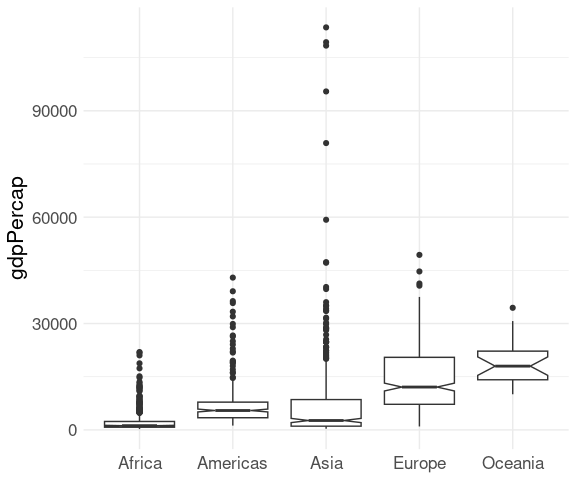
More common is to draw the upper whisker to the largest point below the upper quartile \(+ 1.5 * IQR\) , and the lower whisker analogously.
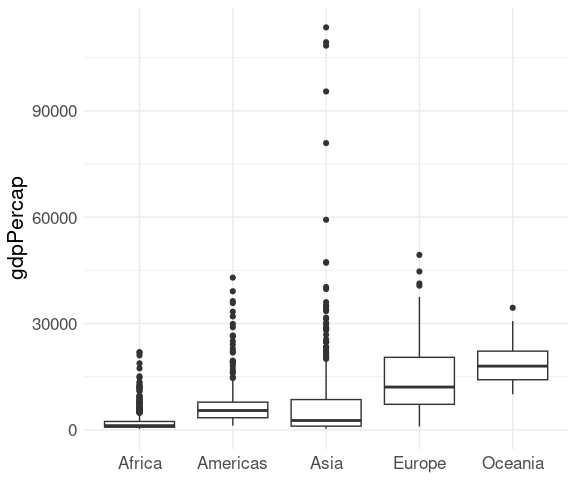
Outliers falling outside the range of the whiskers are then drawn directly:
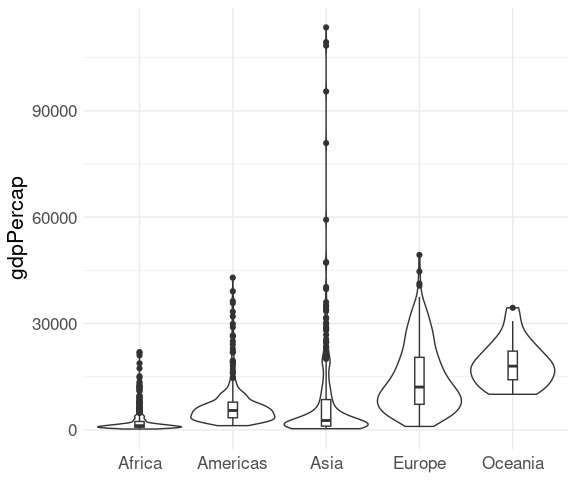
library(gapminder)
library(ggplot2)
ggplot(gapminder) +
geom_boxplot(aes(x = continent, y = gdpPercap)) +
xlab(NULL) +
thm
There are variants that distinguish between mild outliers and extreme outliers .
A common variant is to show an approximate 95% confidence interval for the population median as a notch :
ggplot(gapminder) +
geom_boxplot(aes(x = continent, y = gdpPercap),
notch = TRUE) +
xlab(NULL) +
thm
Another variant is to use a width proportional to the square root of the sample size to reflect the strength of evidence in the data:
ggplot(gapminder) +
geom_boxplot(aes(x = continent, y = gdpPercap),
notch = TRUE, varwidth = TRUE) +
xlab(NULL) +
thm
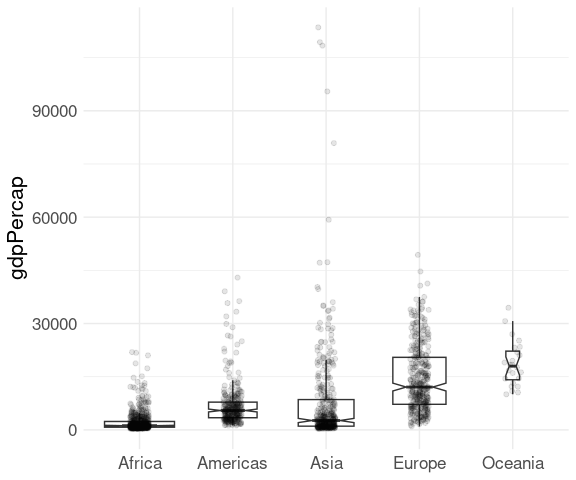
With moderate sample sizes it can be useful to super-impose the original data, perhaps with jittering and alpha blending.
The outliers in the box plot can be turned off with outlier.color = NA so they are not shown twice:
p <- ggplot(gapminder) +
geom_boxplot(aes(x = continent, y = gdpPercap),
notch = TRUE, varwidth = TRUE,
outlier.color = NA) +
xlab(NULL) +
thm
p + geom_point(aes(x = continent, y = gdpPercap),
position =
position_jitter(width = 0.1),
alpha = 0.1)
Violin Plots
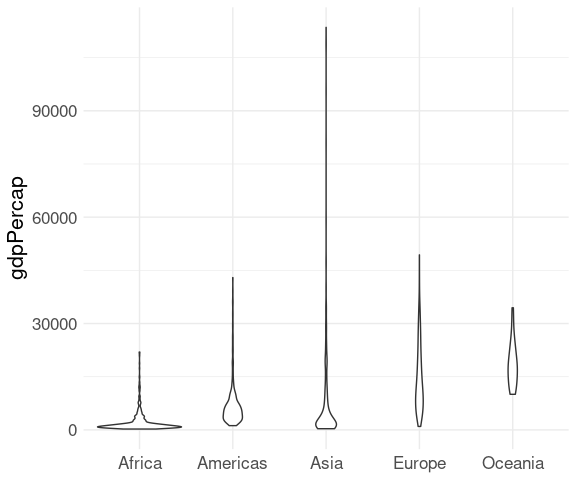
A variant of the boxplot is the violin plot :
Hintze, J. L., Nelson, R. D. (1998), “Violin Plots: A Box Plot-Density Trace Synergism,” The American Statistician 52, 181-184.
The violin plot uses density estimates to show the distributions:
ggplot(gapminder) +
geom_violin(aes(x = continent, y = gdpPercap)) +
xlab(NULL) +
thm
By default the “violins” are scaled to have the same area.
They can also be scaled to have the same maximum height or to have areas proportional to sample sizes.
This is done by adding
scale = "width" orscale = "count"
to the geom_violin call.
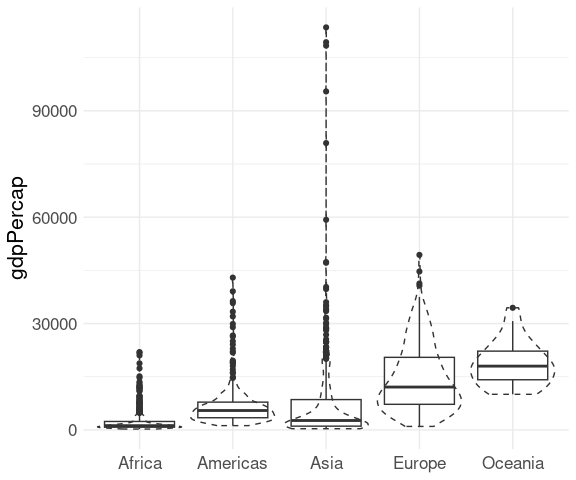
A comparison of boxplots and violin plots:
ggplot(gapminder) +
geom_boxplot(aes(x = continent, y = gdpPercap)) +
geom_violin(aes(x = continent, y = gdpPercap),
fill = NA, scale = "width",
linetype = 2) +
xlab(NULL) +
thm
A combination of boxplots and violin plots:
ggplot(gapminder) +
geom_violin(aes(x = continent, y = gdpPercap),
scale = "width") +
geom_boxplot(aes(x = continent, y = gdpPercap),
width = .1) +
xlab(NULL) +
thm
There are other variations, e.g. vase plots .
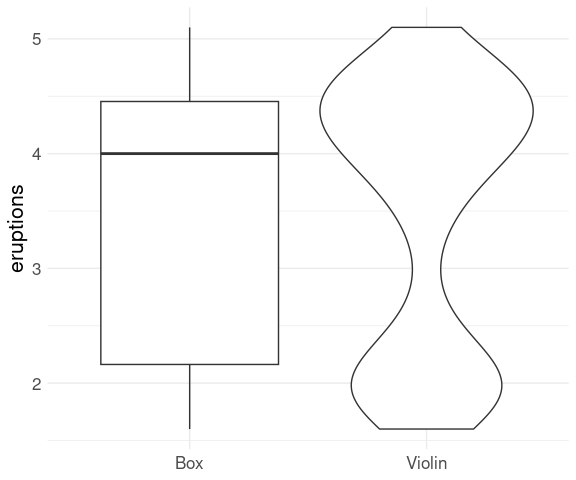
Boxplots do not reflect the shape of a distribution.
For the eruptions in the faithful data set:
ggplot(faithful) +
geom_boxplot(aes(y = eruptions, x = "Box")) +
geom_violin(aes(y = eruptions, x = "Violin"),
trim = FALSE) +
xlab(NULL) +
thm
Swarm Plots
Swarm plots show the full data in a form that also shows the density.
There are a number of variations and names, including beeswarm plots , violin scatterplots , violin strip charts , and sina plots
Sina plots are available as geom_sina in the ggforce package:
library(ggforce)
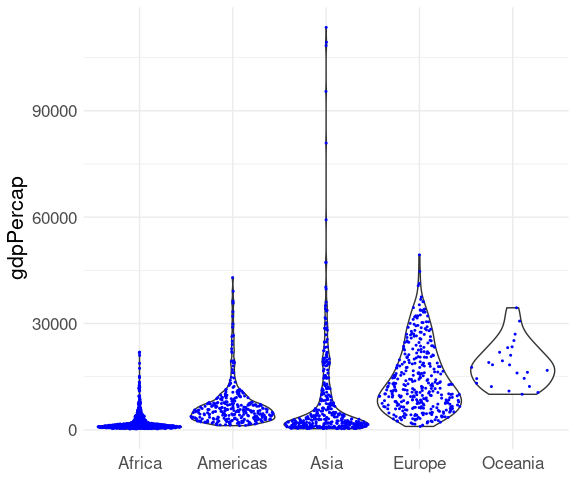
ggplot(gapminder,
aes(x = continent, y = gdpPercap)) +
geom_sina(size = 0.2) +
xlab(NULL) +
thm
Combined with a width-scaled violin plot:
ggplot(gapminder,
aes(x = continent, y = gdpPercap)) +
geom_violin(scale = "width") +
geom_sina(color = "blue",
size = 0.4,
scale = FALSE) +
xlab(NULL) +
thm
Effectiveness and Scalability
Boxplots are very simple and easy to compare.
Boxplots strongly emphasize the middle half of the data.
Boxplots may not be easy for a lay viewer to understand.
Box plots scale fairly well visually and computationally in the number of observations; over-plotting/storage of outliers becomes an issue for larger data sets
Violin plots scale well both visually and computationally in the number of observations.
library(patchwork)
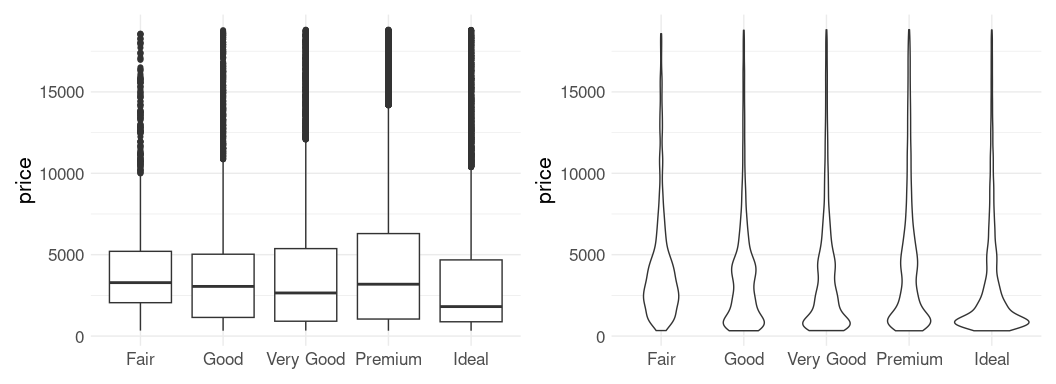
p1 <- ggplot(diamonds) +
geom_boxplot(aes(x = cut, y = price)) +
xlab(NULL) +
thm
p2 <- ggplot(diamonds) +
geom_violin(aes(x = cut, y = price)) +
xlab(NULL) +
thm
p1 + p2
library(lattice)
p1 <- ggplot(barley) +
geom_boxplot(aes(x = site, y = yield, fill = year)) +
xlab(NULL) +
thm
p2 <- ggplot(barley) +
geom_violin(aes(x = site, y = yield, fill = year)) +
xlab(NULL) +
thm
p1 + p2
Axes can be flipped to avoid overplotting of labels:
library(lattice)
p3 <- p1 + coord_flip() + guides(fill = "none")
p4 <- p2 + coord_flip()
p3 + p4
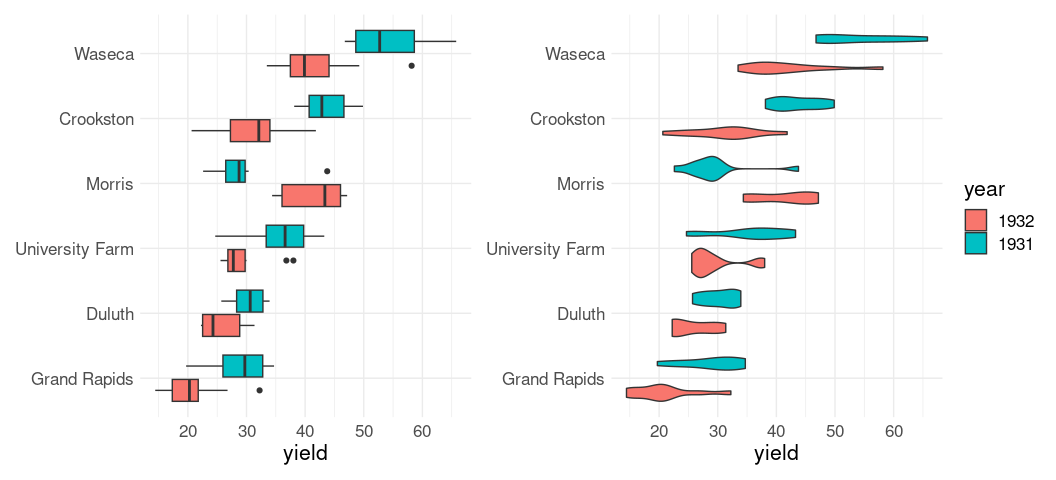
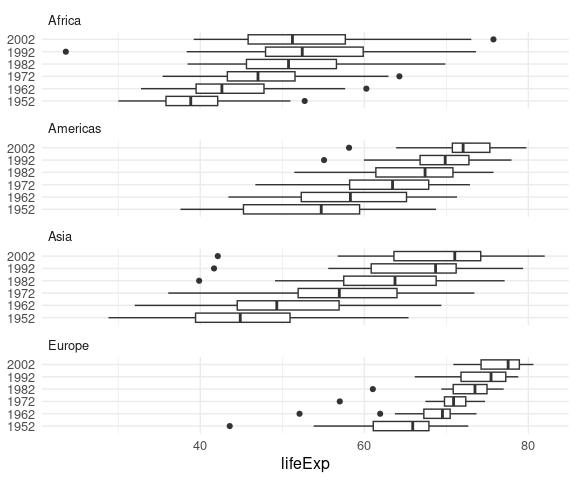
Faceting can also be used to arrange groups of boxplots or violin plots.
For life expectancy by continent over the years in the gapminder data:
library(dplyr)
ggplot(filter(gapminder,
year %% 10 == 2,
continent != "Oceania")) +
geom_boxplot(aes(x = lifeExp, y = factor(year))) +
facet_wrap(~ continent, ncol = 1) +
theme_minimal() +
theme(text = element_text(size = 12)) +
theme(strip.text.x = element_text(hjust = 0)) +
ylab(NULL)
A related visualization motivated by a graph in the Economist is available here
Ridgeline Plots
Ridgeline plots , also called ridge plots or joy plots , are another way to show density estimates for a number of groups that has become popular recently.
An early example appears in this NYT article .
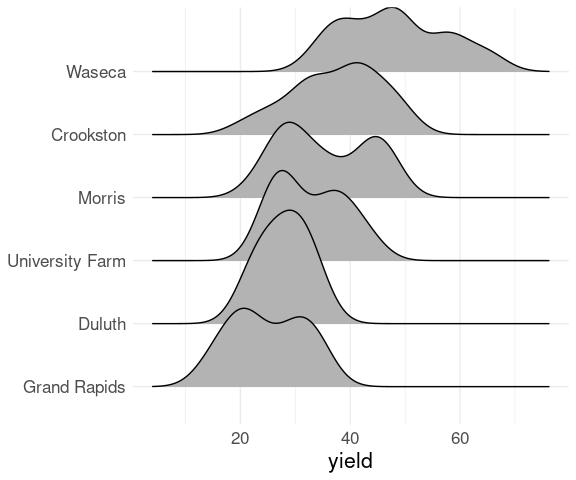
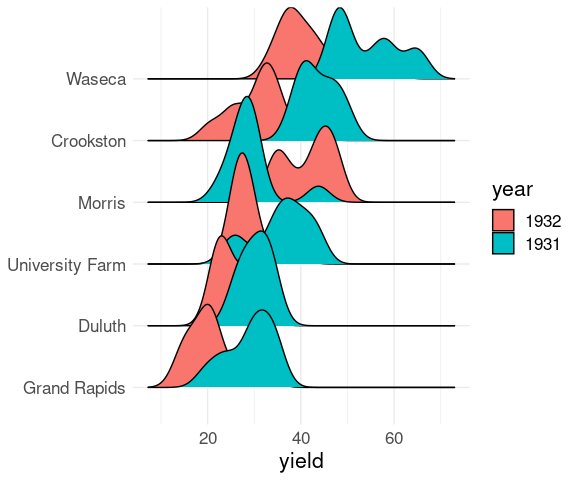
The package ggridges defines geom_density_ridges for creating these plots:
library(ggridges)
ggplot(barley) +
geom_density_ridges(aes(x = yield,
y = site,
group = site)) +
ylab(NULL) +
thm
Grouping by an interaction with a categorical variable, year, produces separate density estimates for each level.
Mapping the fill aesthetic to year allows the separate densities to be identified:
ggplot(barley) +
geom_density_ridges(
aes(x = yield,
y = site,
group = interaction(year, site),
fill = year)) +
ylab(NULL) +
thm
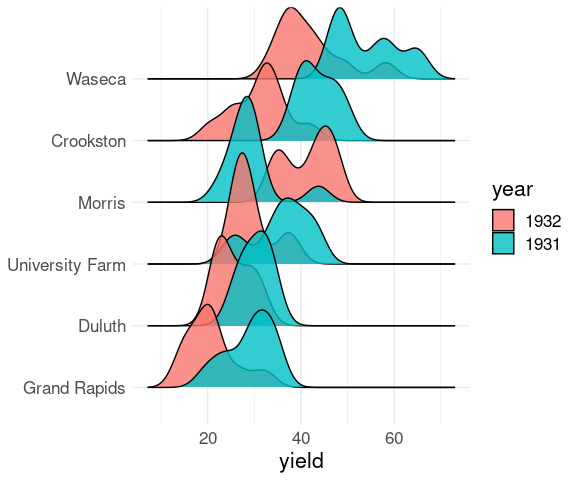
Alpha blending may sometimes help:
ggplot(barley) +
geom_density_ridges(
aes(x = yield,
y = site,
group = interaction(year, site),
fill = year),
alpha = 0.8) +
ylab(NULL) +
thm
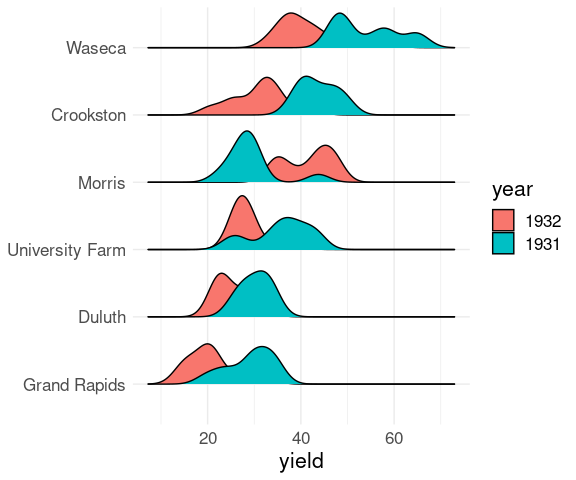
Adjusting the vertical scale may also help:
ggplot(barley) +
geom_density_ridges(
aes(x = yield,
y = site,
group = interaction(year, site),
fill = year),
scale = 0.8) +
ylab(NULL) +
thm
Sometimes reordering the grouping variable, year in this case, can help.
The factor levels of year can be reordered to match the order of average yealds within each year by
reorder(year, yield)Using -yield produces the reverse order.
library(dplyr)
ggplot(mutate(barley, year = reorder(year, -yield))) +
geom_density_ridges(aes(x = yield, y = site,
group = interaction(year, site),
fill = year),
scale = 0.8) +
ylab(NULL) +
thm
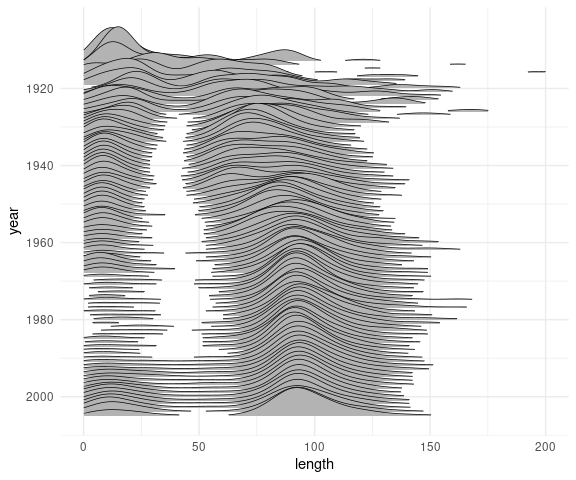
With some tuning ridgeline plots can scale well to many distributions. An example from Claus Wilke’s book :
The ggplot2movies package provides data from IMDB on a large number of movies, including their lengths, in a tibble movies:
library(ggplot2movies)
dim(movies)
## [1] 58788 24
head(movies)
## # A tibble: 6 × 24
## title year length budget rating votes r1 r2 r3 r4 r5 r6
## <chr> <int> <int> <int> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 $ 1971 121 NA 6.4 348 4.5 4.5 4.5 4.5 14.5 24.5
## 2 $1000 a … 1939 71 NA 6 20 0 14.5 4.5 24.5 14.5 14.5
## 3 $21 a Da… 1941 7 NA 8.2 5 0 0 0 0 0 24.5
## 4 $40,000 1996 70 NA 8.2 6 14.5 0 0 0 0 0
## 5 $50,000 … 1975 71 NA 3.4 17 24.5 4.5 0 14.5 14.5 4.5
## 6 $pent 2000 91 NA 4.3 45 4.5 4.5 4.5 14.5 14.5 14.5
## # ℹ 12 more variables: r7 <dbl>, r8 <dbl>, r9 <dbl>, r10 <dbl>, mpaa <chr>,
## # Action <int>, Animation <int>, Comedy <int>, Drama <int>,
## # Documentary <int>, Romance <int>, Short <int>A ridgeline plot of the movie lengths for each year:
library(dplyr)
mv12 <- filter(movies, year > 1912)
ggplot(mv12, aes(x = length, y = year, group = year)) +
geom_density_ridges(scale = 10,
linewidth = 0.25,
rel_min_height = 0.03,
na.rm = TRUE) +
scale_x_continuous(limits = c(0, 200)) +
scale_y_reverse(breaks = c(2000, 1980, 1960,
1940, 1920)) +
theme_minimal()
This shows that since the early 1960’s feature film lengths have stabilized to a distribution centered around 90 minutes:
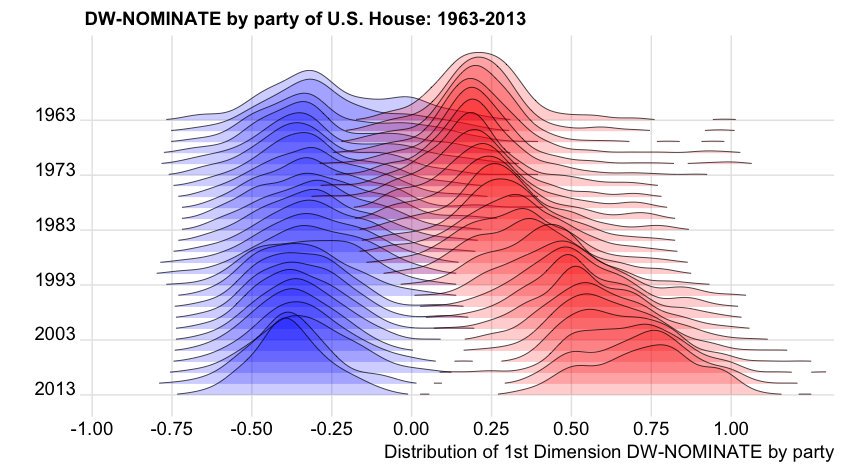
Another nice example: DW-NOMINATE scores for measuring political position of members of congress over the years:
Original code by Ian McDonald; another version is provided in Claus Wilke’s book .
Interactive Tutorial
An interactive learnravailable .
You can run the tutorial with
STAT4580::runTutorial("dists")You can install the current version of the STAT4580 package with
remotes::install_gitlab("luke-tierney/STAT4580")You may need to install the remotes package from CRAN first.
Exercises
Consider the code
``` r
library(ggplot2)
data(Galton, package = "HistData")
ggplot(Galton, aes(x = parent)) +
geom_histogram(---, fill = "grey", color = "black")
```Which of the following replacements for `---` produces a histogram
with bins that are one inch wide and start at whole integers?
a. `binwidth = 1`
b. `binwidth = 1, center = 66.5`
c. `binwidth = 2, center = 66`
d. `center = 66`
Consider the code
library(ggplot2)
ggplot(faithful, aes(x = eruptions)) + geom_density(---)Which of the following replacements for --- produces a density plot with the area under the density in blue and no black border?
color = "lightblue"fill = "black", color = "lightblue"fill = "lightblue", color = NAfill = NA, color = "black" Consider the code
library(ggplot2)
library(gapminder)
p <- ggplot(gapminder, aes(y = continent, x = lifeExp))Which of the following produces violin plots without trimming at the smallest and largest observations, and including a line at the median?
p + geom_violin(trim = FALSE)p + geom_violin(trim = TRUE, show_median = TRUE)p + geom_violin(trim = FALSE, draw_quantiles = 0.5)p + geom_violin(trim = TRUE, show_quantiles = 0.5) Density ridges can also show quantiles, but the details of how to request this are different. Consider this code:
library(ggplot2)
library(ggridges)
library(gapminder)
ggplot(gapminder, aes(x = lifeExp, y = year, group = year)) +
geom_density_ridges(---)Which of the following replacements for --- produces density ridges with lines showing the locations of the medians?
quantiles = 0.5quantile_lines = TRUE, quantiles = 0.5quantile_lines = TRUEdraw_quantiles = 0.5
LS0tCnRpdGxlOiAiVmlzdWFsaXppbmcgRGlzdHJpYnV0aW9ucyIKb3V0cHV0OgogIGh0bWxfZG9jdW1lbnQ6CiAgICB0b2M6IHllcwogICAgY29kZV9mb2xkaW5nOiBzaG93CiAgICBjb2RlX2Rvd25sb2FkOiB0cnVlCi0tLQoKPGxpbmsgcmVsPSJzdHlsZXNoZWV0IiBocmVmPSJzdGF0NDU4MC5jc3MiIHR5cGU9InRleHQvY3NzIiAvPgo8IS0tIHRpdGxlIGJhc2VkIG9uIFdpbGtlJ3MgY2hhcHRlciAtLT4KCmBgYHtyIHNldHVwLCBpbmNsdWRlID0gRkFMU0UsIG1lc3NhZ2UgPSBGQUxTRX0Kc291cmNlKGhlcmU6OmhlcmUoInNldHVwLlIiKSkKa25pdHI6Om9wdHNfY2h1bmskc2V0KGNvbGxhcHNlID0gVFJVRSwgbWVzc2FnZSA9IEZBTFNFLAogICAgICAgICAgICAgICAgICAgICAgZmlnLmhlaWdodCA9IDUsIGZpZy53aWR0aCA9IDYsIGZpZy5hbGlnbiA9ICJjZW50ZXIiKQoKc2V0LnNlZWQoMTIzNDUpCmxpYnJhcnkoZHBseXIpCmxpYnJhcnkoZ2dwbG90MikKbGlicmFyeShsYXR0aWNlKQpsaWJyYXJ5KGdyaWRFeHRyYSkKc291cmNlKGhlcmU6OmhlcmUoImRhdGFzZXRzLlIiKSkKYGBgCgoKIyMgSW50cm9kdWN0aW9uCgpPbmNlIHRoZXJlIGFyZSBtb3JlIHRoYW4gYSBoYW5kZnVsIG9mIG51bWVyaWMgZGF0YSB2YWx1ZXMgaXQgaXMgb2Z0ZW4KdXNlZnVsIHRvIHN0ZXAgYmFjayBhbmQgbG9vayBhdCB0aGUgX2Rpc3RyaWJ1dGlvbl8gb2YgdGhlIGRhdGEgdmFsdWVzOgoKKiBXaGVyZSBpcyB0aGUgYnVsayBvZiB0aGUgZGF0YSBsb2NhdGVkPwoKKiBJcyB0aGVyZSBhIHNpbmdsZSBhcmVhIG9mIGNvbmNlbnRyYXRpb24gb3IgYXJlIHRoZXJlIHNldmVyYWw/CgoqIElzIHRoZSBkYXRhIGRpc3RyaWJ1dGlvbiBzeW1tZXRyaWMgb3IgaXMgaXQgc2tld2VkLCBpLmUuIHRyYWlscyBvZmYKICBtb3JlIHNsb3dseSBpbiBvbmUgZGlyZWN0aW9uIG9yIGFub3RoZXI/CgoqIEFyZSB0aGVyZSBleHRyZW1lLCBvciBvdXRseWluZywgdmFsdWVzPwoKKiBBcmUgdGhlcmUgYW55IHN1c3BpY2lvdXMgb3IgaW1wb3NzaWJsZSB2YWx1ZXM/CgoqIEFyZSB0aGVyZSBnYXBzIGluIHRoZSBkYXRhPwoKKiBJcyB0aGVyZSByb3VuZGluZywgZS5nLiB0byBpbnRlZ2VyIHZhbHVlcywgb3IgX2hlYXBpbmdfLCBpLmUuIGEKICBmZXcgcGFydGljdWxhciB2YWx1ZXMgb2NjdXIgdmVyeSBmcmVxdWVudGx5PwoKUGxvdHMgZm9yIHZpc3VhbGl6aW5nIGRpc3RyaWJ1dGlvbnMgaW5jbHVkZQoKKiBTdHJpcCBwbG90cy4KCiogSGlzdG9ncmFtcy4KCiogRGVuc2l0eSBwbG90cy4KCiogQm94IHBsb3RzLgoKKiBWaW9saW4gcGxvdHMuCgoqIFN3YXJtIHBsb3RzLgoKKiBEZW5zaXR5IHJpZGdlcwoKCiMjIFN0cmlwIFBsb3RzCgoKIyMjIFN0cmlwIFBsb3QgQmFzaWNzCgpBIHZhcmlhbnQgb2YgdGhlIGRvdCBwbG90IGlzIGtub3duIGFzIGEgX3N0cmlwIHBsb3RfLgoKQSBzdHJpcCBwbG90IGZvciB0aGUgY2l0eSB0ZW1wZXJhdHVyZSBkYXRhIGlzCgpgYGB7ciwgZmlnLmhlaWdodCA9IDIsIHdhcm5pbmcgPSBGQUxTRSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnRobSA8LSB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWUodGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gMTYpKQpnZ3Bsb3QoY2l0eXRlbXBzKSArCiAgICBnZW9tX3BvaW50KGFlcyh4ID0gdGVtcCwgeSA9ICJBbGwiKSkgKwogICAgdGhtICsKICAgIHRoZW1lKGF4aXMudGl0bGUueSA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGV4dC55ID0gZWxlbWVudF9ibGFuaygpKQpgYGAKClRoZSBzdHJpcCBwbG90IGNhbiByZXZlYWwgZ2FwcyBhbmQgb3V0bGllcnMuCgpBZnRlciBsb29raW5nIGF0IHRoZSBwbG90IHdlIG1pZ2h0IHdhbnQgdG8gZXhhbWluZSB0aGUgaGlnaCBhbmQKbG93IHZhbHVlczoKCmBgYHtyfQpmaWx0ZXIoY2l0eXRlbXBzLCB0ZW1wID4gODUpCmZpbHRlcihjaXR5dGVtcHMsIHRlbXAgPCAxMCkKYGBgCgpGb3IgdGhlIGVydXB0aW9uIGR1cmF0aW9ucyBpbiB0aGUgYGZhaXRoZnVsYCBkYXRhIGEgc3RyaXAgcGxvdCBzaG93cwp0aGUgdHdvIG1vZGVzIGFyb3VuZCAyIGFuZCA0IG1pbnV0ZXM6CgpgYGB7ciwgZmlnLmhlaWdodCA9IDIsIHdhcm5pbmcgPSBGQUxTRSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChmYWl0aGZ1bCkgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IGVydXB0aW9ucywgeSA9ICJBbGwiKSkgKwogICAgdGhtICsKICAgIHRoZW1lKGF4aXMudGl0bGUueSA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGV4dC55ID0gZWxlbWVudF9ibGFuaygpKQpgYGAKCgojIyMgTXVsdGlwbGUgR3JvdXBzCgpTdHJpcCAgcGxvdHMgYXJlIG1vc3QgdXNlZnVsIGZvciBzaG93aW5nIHN1YnNldHMgY29ycmVzcG9uZGluZyB0byBhCmNhdGVnb3JpY2FsIHZhcmlhYmxlLgoKQSBzdHJpcCBwbG90IGZvciB0aGUgeWllbGRzIGZvciBkaWZmZXJlbnQgdmFyaWV0aWVzIGluIHRoZSBiYXJsZXkgZGF0YQppcwoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoYmFybGV5KSArCiAgICBnZW9tX3BvaW50KGFlcyh4ID0geWllbGQsIHkgPSB2YXJpZXR5KSkgKwogICAgdGhlbWVfbWluaW1hbCgpICsKICAgIHRobQpgYGAKCgojIyMgU2NhbGFiaWxpdHkKClNjYWxhYmlsaXR5IGluIHRoaXMgZm9ybSBpcyBsaW1pdGVkIGR1ZSB0byBvdmVyLXBsb3R0aW5nLgoKQSBzaW1wbGUgc3RyaXAgcGxvdCBvZiBgcHJpY2VgIHdpdGhpbiB0aGUgZGlmZmVyZW50IGBjdXRgIGxldmVscyBpbgp0aGUgYGRpYW1vbmRzYCBkYXRhIGlzIG5vdCB2ZXJ5IGhlbHBmdWw6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcykgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IHByaWNlLCB5ID0gY3V0KSkgKwogICAgdGhtICsKICAgIHRoZW1lKGF4aXMudGl0bGUueSA9IGVsZW1lbnRfYmxhbmsoKSkKYGBgCgpTZXZlcmFsIGFwcHJvYWNoZXMgYXJlIGF2YWlsYWJsZSB0byByZWR1Y2UgdGhlIGltcGFjdCBvZiBvdmVyLXBsb3R0aW5nOgoKKiByZWR1Y2UgdGhlIHBvaW50IHNpemU7CgoqIHJhbmRvbSBkaXNwbGFjZW1lbnQgb2YgcG9pbnRzLCBjYWxsZWQgX2ppdHRlcmluZ187CgoqIG1ha2luZyB0aGUgcG9pbnRzIHRyYW5zbHVjZW50LCBvciBfYWxwaGEgYmxlbmRpbmdfLgoKQ29tYmluaW5nIGFsbCB0aHJlZSBmb3IgZXhhbWluaW5nIGBwcmljZWAgd2l0aGluIGBjdXRgIGZvciB0aGUKYGRpYW1vbmRzYCBkYXRhIHByb2R1Y2VzCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcykgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IHByaWNlLCB5ID0gY3V0KSwKICAgICAgICAgICAgICAgc2l6ZSA9IDAuMiwKICAgICAgICAgICAgICAgcG9zaXRpb24gPSBwb3NpdGlvbl9qaXR0ZXIod2lkdGggPSAwKSwKICAgICAgICAgICAgICAgYWxwaGEgPSAwLjIpICsKICAgIHRobSArIHRoZW1lKGF4aXMudGl0bGUueSA9IGVsZW1lbnRfYmxhbmsoKSkKYGBgCgpTa2V3bmVzcyBvZiB0aGUgcHJpY2UgZGlzdHJpYnV0aW9ucyBjYW4gYmUgc2VlbiBpbiB0aGlzIHBsb3QsIHRob3VnaApvdGhlciBhcHByb2FjaGVzIHdpbGwgc2hvdyB0aGlzIG1vcmUgY2xlYXJseS4KCkEgcGVjdWxpYXIgZmVhdHVyZSByZXZlbGVkIGJ5IHRoaXMgcGxvdCBpcyB0aGUgZ2FwIGJlbG93CjIwMDAuCgpFeGFtaW5pbmcgdGhlIHN1YnNldCB3aXRoIGBwcmljZSA8IDIwMDBgIHNob3dzIHRoZSBnYXAgaXMKcm91Z2hseSBzeW1tZXRyaWMgYXJvdW5kIDE1MDA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChmaWx0ZXIoZGlhbW9uZHMsIHByaWNlIDwgMjAwMCkpICsKICAgIGdlb21fcG9pbnQoYWVzKHggPSBwcmljZSwgeSA9IGN1dCksCiAgICAgICAgICAgICAgIHNpemUgPSAwLjIsCiAgICAgICAgICAgICAgIHBvc2l0aW9uID0gcG9zaXRpb25faml0dGVyKHdpZHRoID0gMCksCiAgICAgICAgICAgICAgIGFscGhhID0gMC4yKSArCiAgICB0aG0gKwogICAgdGhlbWUoYXhpcy50aXRsZS55ID0gZWxlbWVudF9ibGFuaygpKQpgYGAKCkEgcGxvdCBhbG9uZyB0aGVzZSBsaW5lcyB3YXMgdXNlZCBvbiB0aGUgTmV3IFlvcmsgVGltZXMgW2Zyb250IHBhZ2UgZm9yCkZlYnJ1YXJ5IDIxLCAyMDIxXShgciBJTUcoIk5ZVC0yMDIxLTAyLTIxLmpwZWciKWApLgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjU1JSJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygiTllULTIwMjEtMDItMjEuanBlZyIpKQpgYGAKCgojIyMgU29tZSBOb3RlcwoKKiBXaXRoIGEgZ29vZCBjb21iaW5hdGlvbiBvZiBwb2ludCBzaXplIGNob2ljZSwgaml0dGVyaW5nLCBhbmQgYWxwaGEKICBibGVuZGluZyB0aGUgc3RyaXAgcGxvdCBmb3IgZ3JvdXBzIG9mIGRhdGEgY2FuIHNjYWxlIHRvIHNldmVyYWwKICBodW5kcmVkIHRob3VzYW5kIG9ic2VydmF0aW9ucyBhbmQgdGVuIHRvIHR3ZW50eSBvZiBncm91cHMuCgoqIEZvciB2ZXJ5IGxhcmdlIGRhdGF0IHNldHMgaXQgY2FuIGJlIHVzZWZ1bCB0byBsb29rIGF0IGEgc3RyaXAgcGxvdAogIG9mIGEgc2FtcGxlIG9mIHRoZSBkYXRhLgoKKiBTdHJpcCBwbG90cyBjYW4gcmV2ZWFsIGdhcHMsIG91dGxpZXJzLCBhbmQgZGF0YSBvdXRzaWRlIG9mIHRoZQogIGV4cGVjdGVkIHJhbmdlLgoKKiBTa2V3bmVzcyBhbmQgbXVsdGktbW9kYWxpdHkgY2FuIGJlIHNlZW4sIGJ1dCBvdGhlciB2aXN1YWxpemF0aW9ucwogIHNob3cgdGhlc2UgbW9yZSBjbGVhcmx5LgoKKiBTdG9yYWdlIG5lZWRlZCBmb3IgdmVjdG9yIGdyYXBoaWNzIGltYWdlcyBncm93cyBsaW5lYXJseSB3aXRoIHRoZQogIG51bWJlciBvZiBvYnNlcnZhdGlvbnMuCgoqIEJhc2UgZ3JhcGhpY3MgcHJvdmlkZXMgYHN0cmlwY2hhcnRgIGFuZCBsYXR0aWNlIHByb3ZpZGVzIGBzdHJpcHBsb3RgLgoKCiMjIEhpc3RvZ3JhbXMKCgojIyMgSGlzdG9ncmFtIEJhc2ljcwoKSGlzdG9yYW1zIGFyZSBjb25zdHJ1Y3RlZCBieSBiaW5uaW5nIHRoZSBkYXRhIGFuZCBjb3VudGluZyB0aGUgbnVtYmVyCm9mIG9ic2VydmF0aW9ucyBpbiBlYWNoIGJpbi4KClRoZSBvYmplY3RpdmUgaXMgdXN1YWxseSB0byB2aXN1YWxpemUgdGhlIHNoYXBlIG9mIHRoZSBkaXN0cmlidXRpb24uCgpUaGUgbnVtYmVyIG9mIGJpbnMgbmVlZHMgdG8gYmUKCiogc21hbGwgZW5vdWdoIHRvIHJldmVhbCBpbnRlcmVzdGluZyBmZWF0dXJlczsKCiogbGFyZ2UgZW5vdWdoIG5vdCB0byBiZSB0b28gbm9pc3kuCgpBIHZlcnkgc21hbGwgYmluIHdpZHRoIGNhbiBiZSB1c2VkIHRvIGxvb2sgZm9yIHJvdW5kaW5nIG9yIGhlYXBpbmcuCgpDb21tb24gY2hvaWNlcyBmb3IgdGhlIHZlcnRpY2FsIHNjYWxlIGFyZToKCiogYmluIGNvdW50cywgb3IgZnJlcXVlbmNpZXM7CgoqIGNvdW50cyBwZXIgdW5pdCwgb3IgZGVuc2l0aWVzLgoKVGhlIGNvdW50IHNjYWxlIGlzIG1vcmUgaW50ZXByZXRhYmxlIGZvciBsYXkgdmlld2Vycy4KClRoZSBkZW5zaXR5IHNjYWxlIGlzIG1vcmUgc3VpdGVkIGZvciBjb21wYXJpc29uIHRvIG1hdGhlbWF0aWNhbApkZW5zaXR5IG1vZGVscy4KCkNvbnN0cnVjdGluZyBoaXN0b2dyYW1zIHdpdGggdW5lcXVhbCBiaW4gd2lkdGhzIGlzIHBvc3NpYmxlIGJ1dApyYXJlbHkgYSBnb29kIGlkZWEuCgoKIyMjIEhpc3RvZ3JhbXMgaW4gUgoKVGhlcmUgYXJlIG1hbnkgd2F5cyB0byBwbG90IGhpc3RvZ3JhbXMgaW4gUjoKCiogdGhlIGBoaXN0KClgIGZ1bmN0aW9uIGluIHRoZSBiYXNlIGBncmFwaGljc2AgcGFja2FnZTsKCiogYHRydWVoaXN0KClgIGluIHBhY2thZ2UgYE1BU1NgOwoKKiBgaGlzdG9ncmFtKClgIGluIHBhY2thZ2UgYGxhdHRpY2VgOwoKKiBgZ2VvbV9oaXN0b2dyYW0oKWAgaW4gcGFja2FnZSBgZ2dwbG90MmAuCgpBIGhpc3RvZ3JhbSBvZiBlcnVwdGlvbiBkdXJhdGlvbnMgZm9yIGFub3RoZXIgZGF0YSBzZXQgb24gT2xkIEZhaXRoZnVsCmVydXB0aW9ucywgdGhpcyBvbmUgZnJvbSBwYWNrYWdlIGBNQVNTYDoKCmBgYHtyLCBtZXNzYWdlID0gVFJVRSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmRhdGEoZ2V5c2VyLCBwYWNrYWdlID0gIk1BU1MiKQpnZ3Bsb3QoZ2V5c2VyKSArCiAgICBnZW9tX2hpc3RvZ3JhbShhZXMoeCA9IGR1cmF0aW9uKSkgKwogICAgdGhtCmBgYAoKVGhlIGRlZmF1bHQgc2V0dGluZ3MgdXNpbmcgYGdlb21faGlzdG9ncmFtYCBhcmUgbGVzcyB0aGFuIGlkZWFsLgoKVXNpbmcgYSBiaW53aWR0aCBvZiAwLjUgYW5kIGN1c3RvbWl6ZWQgYGZpbGxgIGFuZCBgY29sb3JgIHNldHRpbmdzCnByb2R1Y2VzIGEgYmV0dGVyIHJlc3VsdDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGdleXNlcikgKwogICAgZ2VvbV9oaXN0b2dyYW0oYWVzKHggPSBkdXJhdGlvbiksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDAuNSwKICAgICAgICAgICAgICAgICAgIGZpbGwgPSAiZ3JleSIsCiAgICAgICAgICAgICAgICAgICBjb2xvciA9ICJibGFjayIpICsKICAgIHRobQpgYGAKClJlZHVjaW5nIHRoZSBiaW4gd2lkdGggc2hvd3MgYW4gaW50ZXJlc3RpbmcgZmVhdHVyZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGdleXNlcikgKwogICAgZ2VvbV9oaXN0b2dyYW0oYWVzKHggPSBkdXJhdGlvbiksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDAuMDUsCiAgICAgICAgICAgICAgICAgICBmaWxsID0gImdyZXkiLAogICAgICAgICAgICAgICAgICAgY29sb3IgPSAiYmxhY2siKSArCiAgICB0aG0KYGBgCgoqIEVydXB0aW9ucyB3ZXJlIHNvbWV0aW1lcyBjbGFzc2lmaWVkIGFzIF9zaG9ydF8gb3IgX2xvbmdfOyB0aGVzZSB3ZXJlCiAgY29kZWQgYXMgMiBhbmQgNCBtaW51dGVzLgoKKiBGb3IgbWFueSBwdXJwb3NlcyB0aGlzIGtpbmQgb2YgaGVhcGluZyBvciByb3VuZGluZyBkb2VzIG5vdCBtYXR0ZXIuCgoqIEl0IHdvdWxkIG1hdHRlciBpZiB3ZSB3YW50ZWQgdG8gZXN0aW1hdGUgbWVhbnMgYW5kIHN0YW5kYXJkCiAgZGV2aWF0aW9ucyBvZiB0aGUgZHVyYXRpb25zIG9mIHRoZSBsb25nIGFuZCBzaG9ydCBlcnVwdGlvbnMuCgoqIE1vcmUgZGF0YSBhbmQgaW5mb3JtYXRpb24gYWJvdXQgZ2V5c2VycyBpcyBhdmFpbGFibGUgYXQKICBodHRwczovL2dleXNlcnRpbWVzLm9yZy8uCiAgPCEtLSBUSGlzIHNlZW1zIG5vIGxvbmdlciBtYWludGFpbmVkOgogIGh0dHA6Ly93d3cuZ2V5c2Vyc3R1ZHkub3JnL2dleXNlci5hc3B4P3BHZXlzZXJObz1PTERGQUlUSEZVTC4gLS0+CgoqIEZvciBleHBsb3JhdGlvbiB0aGVyZSBpcyBubyBvbmUgImNvcnJlY3QiIGJpbiB3aWR0aCBvciBudW1iZXIgb2YKICBiaW5zLgoKKiBJdCB3b3VsZCBiZSB2ZXJ5IHVzZWZ1bCB0byBiZSBhYmxlIHRvIGNoYW5nZSB0aGlzIHBhcmFtZXRlcgogIGludGVyYWN0aXZlbHkuCgoKIyMjIFN1cGVyaW1wb3NpbmcgYSBEZW5zaXR5CgpBIGhpc3RvZ3JhbSBjYW4gYmUgdXNlZCB0byBjb21wYXJlIHRoZSBkYXRhIGRpc3RyaWJ1dGlvbiB0byBhCnRoZW9yZXRpY2FsIG1vZGVsLCBzdWNoIGFzIGEgbm9ybWFsIGRpc3RyaWJ1dGlvbi4KClRoaXMgcmVxdWlyZXMgdXNpbmcgYSBfZGVuc2l0eSBzY2FsZV8gZm9yIHRoZSB2ZXJ0aWNhbCBheGlzLgoKVGhlIGBHYWx0b25gIGRhdGEgZnJhbWUgaW4gdGhlIGBIaXN0RGF0YWAgcGFja2FnZSBpcyBvbmUgb2Ygc2V2ZXJhbApkYXRhIHNldHMgdXNlZCBieSBHYWx0b24gdG8gc3R1ZHkgdGhlIGhlaWdodHMgb2YgcGFyZW50cyBhbmQgdGhlaXIKY2hpbGRyZW4uCgpBZGRpbmcgYSBub3JtYWwgZGVuc2l0eSBjdXJ2ZSB0byBhIGBnZ3Bsb3RgIGhpc3RvZ3JhbSBpbnZvbHZlczoKCiogY29tcHV0aW5nIHRoZSBwYXJhbWV0ZXJzIG9mIHRoZSBkZW5zaXR5OwoKKiBjcmVhdGluZyB0aGUgaGlzdG9ncmFtIHdpdGggYSBkZW5zaXR5IHNjYWxlIHVzaW5nIHRoZSBjb21wdXRlZAogIHZhcmlhYmxlIGBhZnRlcl9zdGF0KGRlbnNpdHkpYDsKCiogYWRkaW5nIHRoZSBmdW5jdGlvbiBjdXJ2ZSB1c2luZyBgZ2VvbV9mdW5jdGlvbmAsIGBzdGF0X2Z1bmN0aW9uYCwgb3IKICBgZ2VvbV9saW5lYC4KCkNyZWF0ZSB0aGUgaGlzdG9ncmFtIHdpdGggYSBkZW5zaXR5IHNjYWxlIHVzaW5nIHRoZSBfY29tcHV0ZWQgdmFybGFibGVfCmBhZnRlcl9zdGF0KGRlbnNpdHkpYDoKCjwhLS0gaHR0cDovL3N0YWNrb3ZlcmZsb3cuY29tL3F1ZXN0aW9ucy8yNTA3NTQyOC9nZ3Bsb3QyLXN0YXQtZnVuY3Rpb24td2l0aC1jYWxjdWxhdGVkLWFyZ3VtZW50LWZvci1kaWZmZXJlbnQtZGF0YS1zdWJzZXQtaW5zaWRlIC0tPgoKYGBge3IgZ2FsdG9uLWhpc3QsIGV2YWwgPSBGQUxTRX0KZGF0YShHYWx0b24sIHBhY2thZ2UgPSAiSGlzdERhdGEiKQpnZ3Bsb3QoR2FsdG9uKSArCiAgICBnZW9tX2hpc3RvZ3JhbShhZXMoeCA9IHBhcmVudCwKICAgICAgICAgICAgICAgICAgICAgICB5ID0gYWZ0ZXJfc3RhdChkZW5zaXR5KSksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDEsCiAgICAgICAgICAgICAgICAgICBmaWxsID0gImdyZXkiLAogICAgICAgICAgICAgICAgICAgY29sb3IgPSAiYmxhY2siKSArCiAgICB0aG0KYGBgCgpgYGB7ciBnYWx0b24taGlzdCwgZWNobyA9IEZBTFNFfQpgYGAKClRoZW4gY29tcHV0ZSB0aGUgbWVhbiBhbmQgc3RhbmRhcmQgZGV2aWF0aW9uIGFuZCBhZGQgdGhlIG5vcm1hbApkZW5zaXR5IGN1cnZlOgoKYGBge3IgZ2FsdG9uLWhpc3QtZGVucywgZXZhbCA9IEZBTFNFfQpkYXRhKEdhbHRvbiwgcGFja2FnZSA9ICJIaXN0RGF0YSIpCnBfbWVhbiA8LSBtZWFuKEdhbHRvbiRwYXJlbnQpCnBfc2QgPC0gc2QoR2FsdG9uJHBhcmVudCkKcF9kZW5zIDwtIGZ1bmN0aW9uKHgpIGRub3JtKHgsIHBfbWVhbiwgcF9zZCkKZ2dwbG90KEdhbHRvbikgKwogICAgZ2VvbV9oaXN0b2dyYW0oYWVzKHggPSBwYXJlbnQsCiAgICAgICAgICAgICAgICAgICAgICAgeSA9IGFmdGVyX3N0YXQoZGVuc2l0eSkpLAogICAgICAgICAgICAgICAgICAgYmlud2lkdGggPSAxLAogICAgICAgICAgICAgICAgICAgZmlsbCA9ICJncmV5IiwKICAgICAgICAgICAgICAgICAgIGNvbG9yID0gImJsYWNrIikgKwogICAgZ2VvbV9mdW5jdGlvbihmdW4gPSBwX2RlbnMsIGNvbG9yID0gInJlZCIpICsKICAgIHRobQpgYGAKCmBgYHtyIGdhbHRvbi1oaXN0LWRlbnMsIGVjaG8gPSBGQUxTRX0KYGBgCgoKIyMjIE11bHRpcGxlIEdyb3VwcwoKRmFjZXRpbmcgd29ya3Mgd2VsbCBmb3Igc2hvd2luZyBjb21wYXJhdGl2ZSBoaXN0b2dyYW1zIGZvciBtdWx0aXBsZQpncm91cHMuCgpIaXN0b2dyYW1zIG9mIGBwcmljZWAgd2l0aGluIGBjdXRgIGZvciB0aGUgYGRpYW1vbmRzYCBkYXRhOgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21faGlzdG9ncmFtKGFlcyh4ID0gcHJpY2UpLAogICAgICAgICAgICAgICAgICAgYmlud2lkdGggPSAxMDAwLAogICAgICAgICAgICAgICAgICAgY29sb3IgPSAiYmxhY2siLCBmaWxsID0gImdyZXkiKSArCiAgICBmYWNldF93cmFwKH4gY3V0KSArCiAgICB0aG0KYGBgCgpUaGVzZSBoaXN0b2dyYW1zIHNob3cgY291bnRzIG9uIHRoZSB2ZXJ0aWNhbCBheGlzLCBhbmQgdGhlaXIgc2l6ZXMKcmVmbGVjdCB0aGUgdG90YWwgY291bnRzIGZvciB0aGUgZ3JvdXBzLgoKVG9nZXRoZXIgdGhlIHBsb3RzIHJlcHJlc2VudCBhIHZpZXcgb2YgdGhlIGpvaW50IGRpc3RyaWJ1dGlvbiBvZiBgY3V0YAphbmQgYHByaWNlYC4KClN3aXRjaGluZyB0byBhIGRlbnNpdHkgc2NhbGUgYnkgdXNpbmcgYGFmdGVyX3N0YXQoZGVuc2l0eSlgIGZvciB0aGUgYHlgCmFlc3RoZXRpYyBhbGxvd3MgdGhlIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMgb2YgYHByaWNlYCB3aXRoaW4KZ3JvdXBzIHRvIGJlIGNvbXBhcmVkOgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwIDwtIGdncGxvdChkaWFtb25kcykgKwogICAgZ2VvbV9oaXN0b2dyYW0oYWVzKHggPSBwcmljZSwKICAgICAgICAgICAgICAgICAgICAgICB5ID0gYWZ0ZXJfc3RhdChkZW5zaXR5KSksCiAgICAgICAgICAgICAgICAgICBiaW53aWR0aCA9IDEwMDAsCiAgICAgICAgICAgICAgICAgICBjb2xvciA9ICJibGFjayIsCiAgICAgICAgICAgICAgICAgICBmaWxsID0gImdyZXkiKSArCiAgICB0aG0KcCArIGZhY2V0X3dyYXAofiBjdXQpCmBgYAoKQnkgbWFwcGluZyB0aGUgYGZpbGxgIGFlc3RoZXRpYyB0byBgY3V0YCBpdCBpcyBwb3NzaWJsZSB0byBwcm9kdWNlIGEKc3RhY2tlZCBoaXN0b2dyYW0gb3IgYSBzdXBlcmltcG9zZWQgaGlzdG9ncmFtCgoqIGBwb3NpdGlvbiA9ICJzdGFjayJgLCB0aGUgZGVmYXVsdCwgZm9yIHN0YWNrZWQ7CiogYHBvc2l0aW9uID0gImlkZW50aXR5ImAgZm9yIHN1cGVyaW1wb3NlZC4KCkJ1dCBuZWl0aGVyIHdvcmtzIHZlcnkgd2VsbCB2aXN1YWxseS4KCkZvciBjb21wYXJpbmcgbG9jYXRpb25zIG9mIGZlYXR1cmVzIGl0IGNhbiBoZWxwIHRvIGZhY2V0IHdpdGggYSBzaW5nbGUKY29sdW1uLgoKQnV0IHRoaXMgbWF5IGNyZWF0ZSBhc3BlY3QgcmF0aW9zIHRoYXQgYXJlIG5vdCBpZGVhbC4KCmBgYHtyIGhpc3QtZmFjZXQtb25lLWNvbCwgZWNobyA9IEZBTFNFLCBmaWcuaGVpZ2h0ID0gN30KcCArIGZhY2V0X3dyYXAofiBjdXQsIG5jb2wgPSAxKSArCiAgICBjb29yZF9maXhlZCgxLjUgKiAxZTcpCmBgYAoKCiMjIyBTY2FsYWJpbGl0eQoKSGlzdG9ncmFtcyBzY2FsZSB2ZXJ5IHdlbGwuCgoqIFRoZSB2aXN1YWwgcGVyZm9ybWFuY2UgZG9lcyBub3QgZGV0ZXJpb3JhdGUgd2l0aCBpbmNyZWFzaW5nIG51bWJlcnMKICBvZiBvYnNlcnZhdGlvbnMuCgoqIFRoZSBjb21wdXRhdGlvbmFsIGVmZm9ydCBuZWVkZWQgaXMgbGluZWFyIGluIHRoZSBudW1iZXIgb2Ygb2JzZXJ2YXRpb25zLgoKKiBUaGUgYW1vdW50IG9mIHN0b3JhZ2UgbmVlZGVkIGZvciBhbiBpbWFnZSBvYmplY3QgaXMgbGluZWFyIGluIHRoZQogIG51bWJlciBvZiBiaW5zLgoKCiMjIERlbnNpdHkgUGxvdHMKCgojIyMgRGVuc2l0eSBQbG90IEJhc2ljcwoKRGVuc2l0eSBwbG90cyBjYW4gYmUgdGhvdWdodCBvZiBhcyBwbG90cyBvZiBzbW9vdGhlZCBoaXN0b2dyYW1zLgoKVGhlIHNtb290aG5lc3MgaXMgY29udHJvbGxlZCBieSBhIF9iYW5kd2lkdGhfIHBhcmFtZXRlciB0aGF0IGlzCmFuYWxvZ291cyB0byB0aGUgaGlzdG9ncmFtIGJpbndpZHRoLgoKTW9zdCBkZW5zaXR5IHBsb3RzIHVzZSBhIFtfa2VybmVsIGRlbnNpdHkKZXN0aW1hdGVfXShodHRwczovL2VuLndpa2lwZWRpYS5vcmcvd2lraS9LZXJuZWxfZGVuc2l0eV9lc3RpbWF0aW9uKSwKYnV0IHRoZXJlIGFyZSBvdGhlciBwb3NzaWJsZSBzdHJhdGVnaWVzOyBxdWFsaXRhdGl2ZWx5IHRoZSBwYXJ0aWN1bGFyCnN0cmF0ZWd5IHJhcmVseSBtYXR0ZXJzLgoKQSBkZW5zaXR5IHBsb3Qgb2YgdGhlIGBnZXlzZXJgIGBkdXJhdGlvbmAgdmFyaWFibGUgd2l0aCBkZWZhdWx0CmJhbmR3aWR0aDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGdleXNlcikgKwogICAgZ2VvbV9kZW5zaXR5KGFlcyh4ID0gZHVyYXRpb24pKSArCiAgICB0aG0KYGBgCgpVc2luZyBhIHNtYWxsZXIgYmFuZHdpZHRoIHNob3dzIHRoZSBoZWFwaW5nIGF0IDIgYW5kIDQgbWludXRlczoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGdleXNlcikgKwogICAgZ2VvbV9kZW5zaXR5KGFlcyh4ID0gZHVyYXRpb24pLCBidyA9IDAuMDUpICsKICAgIHRobQpgYGAKCkZvciBhIG1vZGVyYXRlIG51bWJlciBvZiBvYnNlcnZhdGlvbnMgYSB1c2VmdWwgYWRkaXRpb24gaXMgYSBqaXR0ZXJlZApfcnVnIHBsb3RfOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZ2V5c2VyKSArCiAgICBnZW9tX2RlbnNpdHkoYWVzKHggPSBkdXJhdGlvbikpICsKICAgIGdlb21fcnVnKGFlcyh4ID0gZHVyYXRpb24sIHkgPSAwKSwKICAgICAgICAgICAgIHBvc2l0aW9uID0KICAgICAgICAgICAgICAgICBwb3NpdGlvbl9qaXR0ZXIoaGVpZ2h0ID0gMCkpICsKICAgIHRobQpgYGAKCgojIyMgU2NhbGFiaWxpdHkKClZpc3VhbCBzY2FsYWJpbGl0eSBpcyB2ZXJ5IGdvb2QuCgpGb3IgdGhlIGBkaWFtb25kc2AgZGF0YSBgcHJpY2VgIHZhcmlhYmxlOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21fZGVuc2l0eShhZXMoeCA9IHByaWNlKSkgKwogICAgdGhtCmBgYAoKRGVuc2l0eSBlc3RpbWF0ZXMgYXJlIGdlbmVyYWxseSBjb21wdXRlZCBhdCBhIGdyaWQgb2YgcG9pbnRzIGFuZAppbnRlcnBvbGF0ZWQuCgpEZWZhdWx0cyBpbiBSIHZhcnkgZnJvbSA1MCB0byA1MTIgcG9pbnRzLgoKQ29tcHV0YXRpb25hbCBlZmZvcnQgZm9yIGEgZGVuc2l0eSBlc3RpbWF0ZSBhdCBhIHBvaW50IGlzIHByb3BvcnRpb25hbAp0byB0aGUgbnVtYmVyIG9mIG9ic2VydmF0aW9ucy4KClN0b3JhZ2UgbmVlZGVkIGZvciBhbiBpbWFnZSBpcyBwcm9wb3J0aW9uYWwgdG8gdGhlIG51bWJlciBvZiBwb2ludHMKd2hlcmUgdGhlIGRlbnNpdHkgaXMgZXN0aW1hdGVkLgoKCiMjIyBNdWx0aXBsZSBHcm91cHMKCkRlbnNpdHkgZXN0aW1hdGVzIGZvciBzZXZlcmFsIGdyb3VwcyBjYW4gYmUgc2hvd24gaW4gYSBzaW5nbGUgcGxvdCBieQptYXBwaW5nIGEgZ3JvdXAgaW5kZXggdG8gYW4gYWVzdGhldGljLCBzdWNoIGFzIGBjb2xvcmA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiYXJsZXkpICsKICAgIGdlb21fZGVuc2l0eShhZXMoeCA9IHlpZWxkLAogICAgICAgICAgICAgICAgICAgICBjb2xvciA9IHNpdGUpKSArCiAgICB0aG0KYGBgCgpVc2luZyBgZmlsbGAgYW5kIGBhbHBoYWAgY2FuIGFsc28gYmUgdXNlZnVsOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoYmFybGV5KSArCiAgICBnZW9tX2RlbnNpdHkoYWVzKHggPSB5aWVsZCwKICAgICAgICAgICAgICAgICAgICAgZmlsbCA9IHNpdGUpLAogICAgICAgICAgICAgICAgIGFscGhhID0gMC4yKQpgYGAKCk11bHRpcGxlIGRlbnNpdGllcyBpbiBhIHNpbmdsZSBwbG90IHdvcmtzIGJlc3Qgd2l0aCBhIHNtYWxsZXIgbnVtYmVyIG9mCmNhdGVnb3JpZXMsIHNheSAyIG9yIDM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiYXJsZXkpICsKICAgIGdlb21fZGVuc2l0eShhZXMoeCA9IHlpZWxkLAogICAgICAgICAgICAgICAgICAgICBmaWxsID0geWVhciksCiAgICAgICAgICAgICAgICAgYWxwaGEgPSAwLjQpICsKICAgIHRobQpgYGAKClVzaW5nIHNtYWxsIG11bHRpcGxlcywgb3IgZmFjZXRpbmcsIG1heSBiZSBhIGJldHRlciBvcHRpb246CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiYXJsZXkpICsgZ2VvbV9kZW5zaXR5KGFlcyh4ID0geWllbGQpKSArIGZhY2V0X3dyYXAofiBzaXRlKSArIHRobQpgYGAKClRoZXNlIGlkZWFzIGNhbiBiZSBjb21iaW5lZDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGJhcmxleSkgKwogICAgZ2VvbV9kZW5zaXR5KGFlcyh4ID0geWllbGQsIGNvbG9yID0geWVhcikpICsKICAgIGZhY2V0X3dyYXAofiBzaXRlKSArCiAgICB0aG0KYGBgCgpUaGVzZSBwbG90cyBhZ2FpbiBzaG93IGxvd2VyIHlpZWxkcyBmb3IgMTkzMiB0aGFuIGZvciAxOTMxIGZvciBhbGwKc2l0ZXMgZXhjZXB0IE1vcnJpcy4KCkRlbnNpdHkgcGxvdHMgZGVmYXVsdCB0byB1c2luZyB0aGUgZGVuc2l0eSBzY2FsZS4KCkZvciB0aGUgZGlhbW9uZHMgZGF0YSBhIGRlbnNpdHkgcGxvdCBvZiBgcHJpY2VgIGZhY2V0ZWQgb24gYGN1dGAgc2hvd3MKdGhlIGNvbmRpdGlvbmFsIGRpc3RyaWJ1dGlvbnMgb2YgYHByaWNlYCBhdCB0aGUgZGlmZmVyZW50IGBjdXRgCmxldmVsczoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGRpYW1vbmRzKSArCiAgICBnZW9tX2RlbnNpdHkoYWVzKHggPSBwcmljZSkpICsKICAgIGZhY2V0X3dyYXAofiBjdXQpICsgdGhtCmBgYAoKTWFwcGluZyB0aGUgYHlgIGFlc3RoZXRpYyB0byBgYWZ0ZXJfc3RhdChjb3VudClgIHNob3dzIHRoZSBqb2ludCBkaXN0cmlidXRpb24Kb2YgYHByaWNlYCBhbmQgYGN1dGA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcykgKwogICAgZ2VvbV9kZW5zaXR5KGFlcyh4ID0gcHJpY2UsCiAgICAgICAgICAgICAgICAgICAgIHkgPSBhZnRlcl9zdGF0KGNvdW50KSkpICsKICAgIGZhY2V0X3dyYXAofiBjdXQpICsgdGhtCmBgYAoKQSBzdGFja2VkIGRlbnNpdHkgcGxvdCBpcyBzb21ldGltZXMgdXNlZnVsIGJ1dCBvZnRlbiBoYXJkIHRvIHJlYWQ6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcykgKwogICAgZ2VvbV9kZW5zaXR5KGFlcyh4ID0gcHJpY2UsCiAgICAgICAgICAgICAgICAgICAgIHkgPSBhZnRlcl9zdGF0KGNvdW50KSwKICAgICAgICAgICAgICAgICAgICAgZmlsbCA9IGN1dCksCiAgICAgICAgICAgICAgICAgcG9zaXRpb24gPSAic3RhY2siKSArCiAgICB0aG0KYGBgCgpBbiBpbnRlcm1lZGlhdGUgb3B0aW9uOiBBIGZhY2V0ZWQgcGxvdCBvbiB0aGUgY291bnQgc2NhbGUgd2l0aCBhIG11dGVkCnBsb3QgZm9yIHRoZSBmdWxsIGRhdGEgdG8gYWxsb3cgcHJvcG9ydGlvbnMgb2YgdGhlIHdob2xlIHRvIGJlCmFzc2Vzc2VkOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21fZGVuc2l0eShhZXMoeCA9IHByaWNlLCB5ID0gYWZ0ZXJfc3RhdChjb3VudCkpLAogICAgICAgICAgICAgICAgIGZpbGwgPSAibGlnaHRncmV5IiwgY29sb3IgPSBOQSwKICAgICAgICAgICAgICAgICBkYXRhID0gbXV0YXRlKGRpYW1vbmRzLCBjdXQgPSBOVUxMKSkgKwogICAgZ2VvbV9kZW5zaXR5KGFlcyh4ID0gcHJpY2UsCiAgICAgICAgICAgICAgICAgICAgIHkgPSBhZnRlcl9zdGF0KGNvdW50KSwKICAgICAgICAgICAgICAgICAgICAgZmlsbCA9IGN1dCksCiAgICAgICAgICAgICAgICAgcG9zaXRpb24gPSAic3RhY2siLCBjb2xvciA9IE5BKSArCiAgICBmYWNldF93cmFwKH4gY3V0KSArCiAgICBzY2FsZV9maWxsX3ZpcmlkaXNfZChndWlkZSA9ICJub25lIikgKwogICAgdGhtCmBgYAoKQSBmaWxsZWQgZGVuc2l0eSBwbG90IHByb3ZpZGVzIGEgdmV3IG9mIHRoZSBjb25kaXRpb25hbCBkaXN0cmlidXRpb24Kb2YgYGN1dGAgYXQgdGhlIGRpZmZlcmVudCBwcmljZSBsZXZlbHM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChkaWFtb25kcykgKwogICAgZ2VvbV9kZW5zaXR5KGFlcyh4ID0gcHJpY2UsIHkgPSBhZnRlcl9zdGF0KGNvdW50KSwgZmlsbCA9IGN1dCksCiAgICAgICAgICAgICAgICAgcG9zaXRpb24gPSAiZmlsbCIpICsKICAgIHlsYWIoTlVMTCkgKwogICAgdGhtCmBgYAoKVGhpcyBpcyBjYWxsZWQgYSBfQ0QgcGxvdF8sIG9yIGEgX2NvbmRpdGlvbmFsIGRlbnNpdHkgcGxvdF8uCgoKIyMjIFNvbWUgTm90ZXMKCkNvbXB1dGF0aW9ucyBhcmUgZ2VuZXJhbGx5IGRvbmUgd2l0aCB0aGUgYmFzZSBSIGZ1bmN0aW9uIGBkZW5zaXR5YC4KCmBwbG90YCBoYXMgYSBtZXRob2QgZm9yIHRoZSByZXN1bHRzIHJldHVybmVkIGJ5IHRoaXMgZnVuY3Rpb24sIHNvIGEKZGVuc2l0eSBwbG90IGNhbiBiZSBjcmVhdGVkIHdpdGgKCmBgYHtyLCBldmFsID0gRkFMU0V9CnBsb3QoZGVuc2l0eShnZXlzZXIkZHVyYXRpb24pKQpgYGAKClRoZSBgbGF0dGljZWAgcGFja2FnZSBwcm92aWRlcyB0aGUgZnVuY3Rpb24gYGRlbnNpdHlwbG90YC4KCgojIyMgSW50ZXJhY3RpdmUgQmFuZHdpZHRoIENob2ljZQoKQmVpbmcgYWJsZSB0byBjaG9zZSB0aGUgYmFuZHdpZHRoIG9mIGEgZGVuc2l0eSBwbG90LCBvciB0aGUgYmlud2lkdGgKb2YgYSBoaXN0b2dyYW0sIGludGVyYWN0aXZlbHkgaXMgdXNlZnVsIGZvciBleHBsb3JhdGlvbi4KCk9uZSB3YXkgdG8gZG8gdGhpcyBpbiBSICh3aGljaCB1bmZvcnR1bmF0ZWx5IGRvZXMgbm90IHdvcmsgb24gdGhlClJTdHVkaW8gc2VydmVyKToKCmBgYHtyLCBldmFsID0gRkFMU0V9CmRhdGEoZ2V5c2VyLCBwYWNrYWdlID0gIk1BU1MiKQpzb3VyY2UoImh0dHBzOi8vc3RhdC51aW93YS5lZHUvfmx1a2UvY2xhc3Nlcy9TVEFUNzQwMC9leGFtcGxlcy90a2RlbnMuUiIpCnRrZGVucyhnZXlzZXIkZHVyYXRpb24sIHRrcnBsb3QgPSBUUlVFKQpgYGAKCkFub3RoZXIgb3B0aW9uOgoKYGBge3IsIGV2YWwgPSBGQUxTRX0KZGF0YShnZXlzZXIsIHBhY2thZ2UgPSAiTUFTUyIpCnNvdXJjZSgiaHR0cHM6Ly9zdGF0LnVpb3dhLmVkdS9+bHVrZS9jbGFzc2VzL1NUQVQ3NDAwL2V4YW1wbGVzL3NoaW55ZGVucy5SIikKc2hpbnlEZW5zKGdleXNlciRkdXJhdGlvbikKYGBgCgo8IS0tCgpnZ3Bsb3QoYmFybGV5KSArCiAgICBnZW9tX2RlbnNpdHkoYWVzKHggPSB5aWVsZCwgeSA9IC1hZnRlcl9zdGF0KGNvdW50KSwgZmlsbCA9IHllYXIpLAogICAgICAgICAgICAgICAgIGRhdGEgPSBmaWx0ZXIoYmFybGV5LCB5ZWFyID09IDE5MzEpKSArCiAgICBnZW9tX2RlbnNpdHkoYWVzKHggPSB5aWVsZCwgeSA9IGFmdGVyX3N0YXQoY291bnQpLCBmaWxsID0geWVhciksCiAgICAgICAgICAgICAgICAgZGF0YSA9IGZpbHRlcihiYXJsZXksIHllYXIgPT0gMTkzMikpICsKICAgIGNvb3JkX2ZsaXAoKQpnZ3Bsb3QoYmFybGV5KSArCiAgICBnZW9tX2RlbnNpdHkoYWVzKHggPSB5aWVsZCwgeSA9IC1hZnRlcl9zdGF0KGRlbnNpdHkpLCBmaWxsID0geWVhciksCiAgICAgICAgICAgICAgICAgZGF0YSA9IGZpbHRlcihiYXJsZXksIHllYXIgPT0gMTkzMSkpICsKICAgIGdlb21fZGVuc2l0eShhZXMoeCA9IHlpZWxkLCBmaWxsID0geWVhciksCiAgICAgICAgICAgICAgICAgZGF0YSA9IGZpbHRlcihiYXJsZXksIHllYXIgPT0gMTkzMikpICsKICAgIGNvb3JkX2ZsaXAoKSArCiAgICBmYWNldF93cmFwKH5zaXRlKQoKCiMjIEZyb20gQ2xhdXMgV2lsa2UncyBib29rOgpkYXRhKFRpdGFuaWMsIHBhY2thZ2UgPSAiU3RhdDJEYXRhIikKbGlicmFyeShkcGx5cikKbGlicmFyeSh0aWR5cikKbGlicmFyeShjb3dwbG90KQpsaWJyYXJ5KGdncGxvdDIpCgpUaXRhbmljIHw+CiAgICBzZWxlY3QoLVNleENvZGUpIHw+CiAgICByZW5hbWUobmFtZSA9IE5hbWUsIGNsYXNzID0gUENsYXNzLCBhZ2UgPSBBZ2UsIHNleCA9IFNleCwKICAgICAgICAgICBzdXJ2aXZlZCA9IFN1cnZpdmVkKSB8PgogICAgbXV0YXRlKG5hbWUgPSBhcy5jaGFyYWN0ZXIobmFtZSksCiAgICAgICAgICAgY2xhc3MgPSBhcy5jaGFyYWN0ZXIoY2xhc3MpLAogICAgICAgICAgIHNleCA9IGFzLmNoYXJhY3RlcihzZXgpKSAtPiB0aXRhbmljX2FsbCAKCiMjdGl0YW5pYyA8LSBzZWxlY3QodGl0YW5pY190cmFpbiwgYWdlID0gQWdlLCBzZXggPSBTZXgpCnRpdGFuaWMgPC0gdGl0YW5pY19hbGwKCmRhdGEuZnJhbWUoCiAgICBhZ2UgPSAoMToyOCkqMyAtIDEuNSwgCiAgICBtYWxlID0gaGlzdChmaWx0ZXIodGl0YW5pYywgc2V4ID09ICJtYWxlIikkYWdlLAogICAgICAgICAgICAgICAgYnJlYWtzID0gKDA6MjgpKjMgKyAuMDEsIHBsb3QgPSBGQUxTRSkkY291bnRzLAogICAgZmVtYWxlID0gaGlzdChmaWx0ZXIodGl0YW5pYywgc2V4ID09ICJmZW1hbGUiKSRhZ2UsCiAgICAgICAgICAgICAgICAgIGJyZWFrcyA9ICgwOjI4KSozICsgLjAxLCBwbG90ID0gRkFMU0UpJGNvdW50cwopIHw+CiAgICBnYXRoZXIoZ2VuZGVyLCBjb3VudCwgLWFnZSkgLT4gZ2VuZGVyX2NvdW50cwoKZ2dwbG90KGdlbmRlcl9jb3VudHMsCiAgICAgICBhZXMoeCA9IGFnZSwgeSA9IGlmZWxzZShnZW5kZXIgPT0gIm1hbGUiLC0xLCAxKSpjb3VudCwgZmlsbCA9IGdlbmRlcikpICsgCiAgICBnZW9tX2NvbCgpICsKICAgIHNjYWxlX3hfY29udGludW91cyhuYW1lID0gImFnZSAoeWVhcnMpIiwgbGltaXRzID0gYygwLCA3NSksCiAgICAgICAgICAgICAgICAgICAgICAgZXhwYW5kID0gYygwLCAwKSkgKwogICAgc2NhbGVfeV9jb250aW51b3VzKG5hbWUgPSAiY291bnQiLCBicmVha3MgPSAyMCooLTI6MSksCiAgICAgICAgICAgICAgICAgICAgICAgbGFiZWxzID0gYygiNDAiLCAiMjAiLCAiMCIsICIyMCIpKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBjKCIjRDU1RTAwIiwgIiMwMDcyQjIiKSwgZ3VpZGUgPSAibm9uZSIpICsKICAgIGRyYXdfdGV4dCh4ID0gNzAsIHkgPSAtMzksICJtYWxlIiwgaGp1c3QgPSAwKSArCiAgICBkcmF3X3RleHQoeCA9IDcwLCB5ID0gMjEsICJmZW1hbGUiLCBoanVzdCA9IDApICsKICAgIGNvb3JkX2ZsaXAoKQotLT4KCgojIyBCb3hwbG90cwoKX0JveHBsb3RzXywgb3IgX2JveC1hbmQtd2hpc2tlcl8gcGxvdHMsIHByb3ZpZGUgYSBza2VsZXRhbApyZXByZXNlbnRhdGlvbiBvZiBhIGRpc3RyaWJ1dGlvbi4KClRoZXkgYXJlIHZlcnkgd2VsbCBzdWl0ZWQgZm9yIHNob3dpbmcgZGlzdHJpYnV0aW9ucyBmb3IgbXVsdGlwbGUKZ3JvdXBzLgoKVGhlcmUgYXJlIG1hbnkgdmFyaWF0aW9ucyBvZiBib3hwbG90czoKCiogTW9zdCBzdGFydCB3aXRoIGEgX2JveF8gZnJvbSB0aGUgZmlyc3QgdG8gdGhlIHRoaXJkIHF1YXJ0aWxlcyBhbmQKICBkaXZpZGVkIGJ5IHRoZSBtZWRpYW4uCgoqIFRoZSBzaW1wbGVzdCBmb3JtIHRoZW4gYWRkcyBhIF93aGlza2VyXyBmcm9tIHRoZSBsb3dlciBxdWFydGlsZSB0byB0aGUKICBtaW5pbXVtIGFuZCBmcm9tIHRoZSB1cHBlciBxdWFydGlsZSB0byB0aGUgbWF4aW11bS4KCiogTW9yZSBjb21tb24gaXMgdG8gZHJhdyB0aGUgdXBwZXIgd2hpc2tlciB0byB0aGUgbGFyZ2VzdCBwb2ludCBiZWxvdwogIHRoZSB1cHBlciBxdWFydGlsZSAkKyAxLjUgKiBJUVIkLCBhbmQgdGhlIGxvd2VyIHdoaXNrZXIgYW5hbG9nb3VzbHkuCgoqIF9PdXRsaWVyc18gZmFsbGluZyBvdXRzaWRlIHRoZSByYW5nZSBvZiB0aGUgd2hpc2tlcnMgYXJlIHRoZW4gZHJhd24KICBkaXJlY3RseToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShnYXBtaW5kZXIpCmxpYnJhcnkoZ2dwbG90MikKZ2dwbG90KGdhcG1pbmRlcikgKwogICAgZ2VvbV9ib3hwbG90KGFlcyh4ID0gY29udGluZW50LCB5ID0gZ2RwUGVyY2FwKSkgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpUaGVyZSBhcmUgdmFyaWFudHMgdGhhdCBkaXN0aW5ndWlzaCBiZXR3ZWVuIF9taWxkIG91dGxpZXJzXyBhbmQKX2V4dHJlbWUgb3V0bGllcnNfLgoKQSBjb21tb24gdmFyaWFudCBpcyB0byBzaG93IGFuIGFwcHJveGltYXRlIDk1JSBjb25maWRlbmNlIGludGVydmFsIGZvcgp0aGUgcG9wdWxhdGlvbiBtZWRpYW4gYXMgYSBfbm90Y2hfOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZ2FwbWluZGVyKSArCiAgICBnZW9tX2JveHBsb3QoYWVzKHggPSBjb250aW5lbnQsIHkgPSBnZHBQZXJjYXApLAogICAgICAgICAgICAgICAgIG5vdGNoID0gVFJVRSkgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpBbm90aGVyIHZhcmlhbnQgaXMgdG8gdXNlIGEgd2lkdGggcHJvcG9ydGlvbmFsIHRvIHRoZSBzcXVhcmUgcm9vdCBvZgp0aGUgc2FtcGxlIHNpemUgdG8gcmVmbGVjdCB0aGUgc3RyZW5ndGggb2YgZXZpZGVuY2UgaW4gdGhlIGRhdGE6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChnYXBtaW5kZXIpICsKICAgIGdlb21fYm94cGxvdChhZXMoeCA9IGNvbnRpbmVudCwgeSA9IGdkcFBlcmNhcCksCiAgICAgICAgICAgICAgICAgbm90Y2ggPSBUUlVFLCB2YXJ3aWR0aCA9IFRSVUUpICsKICAgIHhsYWIoTlVMTCkgKwogICAgdGhtCmBgYAoKV2l0aCBtb2RlcmF0ZSBzYW1wbGUgc2l6ZXMgaXQgY2FuIGJlIHVzZWZ1bCB0byBzdXBlci1pbXBvc2UgdGhlCm9yaWdpbmFsIGRhdGEsIHBlcmhhcHMgd2l0aCBqaXR0ZXJpbmcgYW5kIGFscGhhIGJsZW5kaW5nLgoKVGhlIG91dGxpZXJzIGluIHRoZSBib3ggcGxvdCBjYW4gYmUgdHVybmVkIG9mZiB3aXRoIGBvdXRsaWVyLmNvbG9yID0KTkFgIHNvIHRoZXkgYXJlIG5vdCBzaG93biB0d2ljZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcCA8LSBnZ3Bsb3QoZ2FwbWluZGVyKSArCiAgICBnZW9tX2JveHBsb3QoYWVzKHggPSBjb250aW5lbnQsIHkgPSBnZHBQZXJjYXApLAogICAgICAgICAgICAgICAgIG5vdGNoID0gVFJVRSwgdmFyd2lkdGggPSBUUlVFLAogICAgICAgICAgICAgICAgIG91dGxpZXIuY29sb3IgPSBOQSkgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KcCArIGdlb21fcG9pbnQoYWVzKHggPSBjb250aW5lbnQsIHkgPSBnZHBQZXJjYXApLAogICAgICAgICAgICAgICBwb3NpdGlvbiA9CiAgICAgICAgICAgICAgICAgICBwb3NpdGlvbl9qaXR0ZXIod2lkdGggPSAwLjEpLAogICAgICAgICAgICAgICBhbHBoYSA9IDAuMSkKYGBgCgoKIyMgVmlvbGluIFBsb3RzCgpBIHZhcmlhbnQgb2YgdGhlIGJveHBsb3QgaXMgdGhlIF92aW9saW4gcGxvdF86Cgo+IEhpbnR6ZSwgSi4gTC4sIE5lbHNvbiwgUi4gRC4gKDE5OTgpLCAiVmlvbGluIFBsb3RzOiBBIEJveAo+IFBsb3QtRGVuc2l0eSBUcmFjZSBTeW5lcmdpc20sIiBfVGhlIEFtZXJpY2FuIFN0YXRpc3RpY2lhbl8gNTIsCj4gMTgxLTE4NC4KClRoZSB2aW9saW4gcGxvdCB1c2VzIGRlbnNpdHkgZXN0aW1hdGVzIHRvIHNob3cgdGhlIGRpc3RyaWJ1dGlvbnM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChnYXBtaW5kZXIpICsKICAgIGdlb21fdmlvbGluKGFlcyh4ID0gY29udGluZW50LCB5ID0gZ2RwUGVyY2FwKSkgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpCeSBkZWZhdWx0IHRoZSAidmlvbGlucyIgYXJlIHNjYWxlZCB0byBoYXZlIHRoZSBzYW1lIGFyZWEuCgpUaGV5IGNhbiBhbHNvIGJlIHNjYWxlZCB0byBoYXZlIHRoZSBzYW1lIG1heGltdW0gaGVpZ2h0IG9yIHRvIGhhdmUKYXJlYXMgcHJvcG9ydGlvbmFsIHRvIHNhbXBsZSBzaXplcy4KClRoaXMgaXMgZG9uZSBieSBhZGRpbmcKCiogYHNjYWxlID0gIndpZHRoImAgb3IKKiBgc2NhbGUgPSAiY291bnQiYAoKdG8gdGhlIGBnZW9tX3Zpb2xpbmAgY2FsbC4KCkEgY29tcGFyaXNvbiBvZiBib3hwbG90cyBhbmQgdmlvbGluIHBsb3RzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZ2FwbWluZGVyKSArCiAgICBnZW9tX2JveHBsb3QoYWVzKHggPSBjb250aW5lbnQsIHkgPSBnZHBQZXJjYXApKSArCiAgICBnZW9tX3Zpb2xpbihhZXMoeCA9IGNvbnRpbmVudCwgeSA9IGdkcFBlcmNhcCksCiAgICAgICAgICAgICAgICBmaWxsID0gTkEsIHNjYWxlID0gIndpZHRoIiwKICAgICAgICAgICAgICAgIGxpbmV0eXBlID0gMikgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpBIGNvbWJpbmF0aW9uIG9mIGJveHBsb3RzIGFuZCB2aW9saW4gcGxvdHM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChnYXBtaW5kZXIpICsKICAgIGdlb21fdmlvbGluKGFlcyh4ID0gY29udGluZW50LCB5ID0gZ2RwUGVyY2FwKSwKICAgICAgICAgICAgICAgIHNjYWxlID0gIndpZHRoIikgKwogICAgZ2VvbV9ib3hwbG90KGFlcyh4ID0gY29udGluZW50LCB5ID0gZ2RwUGVyY2FwKSwKICAgICAgICAgICAgICAgICB3aWR0aCA9IC4xKSArCiAgICB4bGFiKE5VTEwpICsKICAgIHRobQpgYGAKClRoZXJlIGFyZSBvdGhlciB2YXJpYXRpb25zLCBlLmcuIF92YXNlIHBsb3RzXy4KCkJveHBsb3RzIGRvIG5vdCByZWZsZWN0IHRoZSBzaGFwZSBvZiBhIGRpc3RyaWJ1dGlvbi4KCkZvciB0aGUgYGVydXB0aW9uc2AgaW4gdGhlIGBmYWl0aGZ1bGAgZGF0YSBzZXQ6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChmYWl0aGZ1bCkgKwogICAgZ2VvbV9ib3hwbG90KGFlcyh5ID0gZXJ1cHRpb25zLCB4ID0gIkJveCIpKSArCiAgICBnZW9tX3Zpb2xpbihhZXMoeSA9IGVydXB0aW9ucywgeCA9ICJWaW9saW4iKSwKICAgICAgICAgICAgICAgIHRyaW0gPSBGQUxTRSkgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KYGBgCgoKIyMgU3dhcm0gUGxvdHMKClN3YXJtIHBsb3RzIHNob3cgdGhlIGZ1bGwgZGF0YSBpbiBhIGZvcm0gdGhhdCBhbHNvIHNob3dzIHRoZSBkZW5zaXR5LgoKVGhlcmUgYXJlIGEgbnVtYmVyIG9mIHZhcmlhdGlvbnMgYW5kIG5hbWVzLCBpbmNsdWRpbmcgX2JlZXN3YXJtCnBsb3RzXywgX3Zpb2xpbiBzY2F0dGVycGxvdHNfLCBfdmlvbGluIHN0cmlwIGNoYXJ0c18sIGFuZCBfc2luYSBwbG90c18KCltTaW5hCnBsb3RzXShodHRwczovL3d3dy50YW5kZm9ubGluZS5jb20vZG9pL2Z1bGwvMTAuMTA4MC8xMDYxODYwMC4yMDE3LjEzNjY5MTQpCmFyZSBhdmFpbGFibGUgYXMgYGdlb21fc2luYWAgaW4gdGhlIGBnZ2ZvcmNlYCBwYWNrYWdlOgoKPCEtLSBodHRwOi8vbW9kZXJuZ3JhcGhpY3MxMS5wYndvcmtzLmNvbS9mL3dpbGtpbnNvbl8xOTk5LkRvdFBsb3RzLnBkZiAtLT4KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShnZ2ZvcmNlKQpnZ3Bsb3QoZ2FwbWluZGVyLAogICAgICAgYWVzKHggPSBjb250aW5lbnQsIHkgPSBnZHBQZXJjYXApKSArCiAgICBnZW9tX3NpbmEoc2l6ZSA9IDAuMikgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpDb21iaW5lZCB3aXRoIGEgd2lkdGgtc2NhbGVkIHZpb2xpbiBwbG90OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZ2FwbWluZGVyLAogICAgICAgYWVzKHggPSBjb250aW5lbnQsIHkgPSBnZHBQZXJjYXApKSArCiAgICBnZW9tX3Zpb2xpbihzY2FsZSA9ICJ3aWR0aCIpICsKICAgIGdlb21fc2luYShjb2xvciA9ICJibHVlIiwKICAgICAgICAgICAgICBzaXplID0gMC40LAogICAgICAgICAgICAgIHNjYWxlID0gRkFMU0UpICsKICAgIHhsYWIoTlVMTCkgKwogICAgdGhtCmBgYAoKCiMjIEVmZmVjdGl2ZW5lc3MgYW5kIFNjYWxhYmlsaXR5CgoqIEJveHBsb3RzIGFyZSB2ZXJ5IHNpbXBsZSBhbmQgZWFzeSB0byBjb21wYXJlLgoKKiBCb3hwbG90cyBzdHJvbmdseSBlbXBoYXNpemUgdGhlIG1pZGRsZSBoYWxmIG9mIHRoZSBkYXRhLgoKKiBCb3hwbG90cyBtYXkgbm90IGJlIGVhc3kgZm9yIGEgbGF5IHZpZXdlciB0byB1bmRlcnN0YW5kLgoKKiBCb3ggcGxvdHMgc2NhbGUgZmFpcmx5IHdlbGwgdmlzdWFsbHkgYW5kIGNvbXB1dGF0aW9uYWxseSBpbiB0aGUKICBudW1iZXIgb2Ygb2JzZXJ2YXRpb25zOyBvdmVyLXBsb3R0aW5nL3N0b3JhZ2Ugb2Ygb3V0bGllcnMgYmVjb21lcyBhbgogIGlzc3VlIGZvciBsYXJnZXIgZGF0YSBzZXRzCgoqIFZpb2xpbiBwbG90cyBzY2FsZSB3ZWxsIGJvdGggdmlzdWFsbHkgYW5kIGNvbXB1dGF0aW9uYWxseSBpbiB0aGUKICBudW1iZXIgb2Ygb2JzZXJ2YXRpb25zLgoKYGBge3IsIGZpZy53aWR0aCA9IDExLCBmaWcuaGVpZ2h0ID0gNCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmxpYnJhcnkocGF0Y2h3b3JrKQpwMSA8LSBnZ3Bsb3QoZGlhbW9uZHMpICsKICAgIGdlb21fYm94cGxvdChhZXMoeCA9IGN1dCwgeSA9IHByaWNlKSkgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KcDIgPC0gZ2dwbG90KGRpYW1vbmRzKSArCiAgICBnZW9tX3Zpb2xpbihhZXMoeCA9IGN1dCwgeSA9IHByaWNlKSkgKwogICAgeGxhYihOVUxMKSArCiAgICB0aG0KcDEgKyBwMgpgYGAKCiogU2NhbGFiaWxpdHkgaW4gdGhlIG51bWJlciBvZiBjYXNlcyBmb3Igc3dhcm0gb3Igc2luYSBwbG90cyBpcyBtb3JlCiAgbGltaXRlZC4KCiogVGhlIG51bWJlciBvZiBncm91cHMgdGhhdCBjYW4gYmUgaGFuZGxlZCBmb3IgY29tcGFyaXNvbiBieSB0aGVzZSBwbG90cwogIGlzIGluIHRoZSByYW5nZSBvZiBhIGZldyBkb3plbi4KCmBgYHtyLCBmaWcud2lkdGggPSAxMSwgZmlnLmhlaWdodCA9IDUsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpsaWJyYXJ5KGxhdHRpY2UpCnAxIDwtIGdncGxvdChiYXJsZXkpICsKICAgIGdlb21fYm94cGxvdChhZXMoeCA9IHNpdGUsIHkgPSB5aWVsZCwgZmlsbCA9IHllYXIpKSArCiAgICB4bGFiKE5VTEwpICsKICAgIHRobQpwMiA8LSBnZ3Bsb3QoYmFybGV5KSArCiAgICBnZW9tX3Zpb2xpbihhZXMoeCA9IHNpdGUsIHkgPSB5aWVsZCwgZmlsbCA9IHllYXIpKSArCiAgICB4bGFiKE5VTEwpICsKICAgIHRobQpwMSArIHAyCmBgYAoKQXhlcyBjYW4gYmUgZmxpcHBlZCB0byBhdm9pZCBvdmVycGxvdHRpbmcgb2YgbGFiZWxzOgoKYGBge3IsIGZpZy53aWR0aCA9IDExLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShsYXR0aWNlKQpwMyA8LSBwMSArIGNvb3JkX2ZsaXAoKSArIGd1aWRlcyhmaWxsID0gIm5vbmUiKQpwNCA8LSBwMiArIGNvb3JkX2ZsaXAoKQpwMyArIHA0CmBgYAoKRmFjZXRpbmcgY2FuIGFsc28gYmUgdXNlZCB0byBhcnJhbmdlIGdyb3VwcyBvZiBib3hwbG90cyBvciB2aW9saW4gcGxvdHMuCgpGb3IgbGlmZSBleHBlY3RhbmN5IGJ5IGNvbnRpbmVudCBvdmVyIHRoZSB5ZWFycyBpbiB0aGUgYGdhcG1pbmRlcmAgZGF0YToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShkcGx5cikKZ2dwbG90KGZpbHRlcihnYXBtaW5kZXIsCiAgICAgICAgICAgICAgeWVhciAlJSAxMCA9PSAyLAogICAgICAgICAgICAgIGNvbnRpbmVudCAhPSAiT2NlYW5pYSIpKSArCiAgICBnZW9tX2JveHBsb3QoYWVzKHggPSBsaWZlRXhwLCB5ID0gZmFjdG9yKHllYXIpKSkgKwogICAgZmFjZXRfd3JhcCh+IGNvbnRpbmVudCwgbmNvbCA9IDEpICsKICAgIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZSh0ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSAxMikpICsKICAgIHRoZW1lKHN0cmlwLnRleHQueCA9IGVsZW1lbnRfdGV4dChoanVzdCA9IDApKSArCiAgICB5bGFiKE5VTEwpCmBgYAoKQSByZWxhdGVkIHZpc3VhbGl6YXRpb24gbW90aXZhdGVkIGJ5IGEgZ3JhcGggaW4gdGhlIEVjb25vbWlzdCBpcwphdmFpbGFibGUgW2hlcmVdKGh0dHBzOi8vZ2l0aHViLmNvbS9ocmJybXN0ci9nZ2Vjb25vZGlzdCkKCgojIyBSaWRnZWxpbmUgUGxvdHMKCltSaWRnZWxpbmUKcGxvdHNdKGh0dHBzOi8vYmxvZy5yZXZvbHV0aW9uYW5hbHl0aWNzLmNvbS8yMDE3LzA3L2pveXBsb3RzLmh0bWwpLAphbHNvIGNhbGxlZCBfcmlkZ2UgcGxvdHNfIG9yIF9qb3kgcGxvdHNfLCBhcmUgYW5vdGhlciB3YXkgdG8gc2hvdwpkZW5zaXR5IGVzdGltYXRlcyBmb3IgYSBudW1iZXIgb2YgZ3JvdXBzIHRoYXQgaGFzIGJlY29tZSBwb3B1bGFyCnJlY2VudGx5LgoKQW4gZWFybHkgZXhhbXBsZSBhcHBlYXJzIGluIFt0aGlzIE5ZVAphcnRpY2xlXShodHRwczovL3d3dy5ueXRpbWVzLmNvbS9pbnRlcmFjdGl2ZS8yMDE3LzA2LzEyL3Vwc2hvdC90aGUtcG9saXRpY3Mtb2YtYW1lcmljYXMtcmVsaWdpb3VzLWxlYWRlcnMuaHRtbCkuCjwhLS0gZWFybHkgUiB2ZXJzaW9uIGluIC0gaHR0cHM6Ly9sdWlzZHZhLmdpdGh1Yi5pby9yc3RhdHMvZGVuc2l0eS1zd2FybXMvIC0tPgoKVGhlIHBhY2thZ2UgYGdncmlkZ2VzYCBkZWZpbmVzIGBnZW9tX2RlbnNpdHlfcmlkZ2VzYCBmb3IgY3JlYXRpbmcKdGhlc2UgcGxvdHM6CgpgYGB7ciwgbWVzc2FnZSA9IEZBTFNFLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShnZ3JpZGdlcykKZ2dwbG90KGJhcmxleSkgKwogICAgZ2VvbV9kZW5zaXR5X3JpZGdlcyhhZXMoeCA9IHlpZWxkLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgeSA9IHNpdGUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICBncm91cCA9IHNpdGUpKSArCiAgICB5bGFiKE5VTEwpICsKICAgIHRobQpgYGAKCkdyb3VwaW5nIGJ5IGFuIGludGVyYWN0aW9uIHdpdGggYSBjYXRlZ29yaWNhbCB2YXJpYWJsZSwgYHllYXJgLApwcm9kdWNlcyBzZXBhcmF0ZSBkZW5zaXR5IGVzdGltYXRlcyBmb3IgZWFjaCBsZXZlbC4KCk1hcHBpbmcgdGhlIGBmaWxsYCBhZXN0aGV0aWMgdG8gYHllYXJgIGFsbG93cyB0aGUgc2VwYXJhdGUgZGVuc2l0aWVzCnRvIGJlIGlkZW50aWZpZWQ6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiYXJsZXkpICsKICAgIGdlb21fZGVuc2l0eV9yaWRnZXMoCiAgICAgICAgYWVzKHggPSB5aWVsZCwKICAgICAgICAgICAgeSA9IHNpdGUsCiAgICAgICAgICAgIGdyb3VwID0gaW50ZXJhY3Rpb24oeWVhciwgc2l0ZSksCiAgICAgICAgICAgIGZpbGwgPSB5ZWFyKSkgKwogICAgeWxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpBbHBoYSBibGVuZGluZyBtYXkgc29tZXRpbWVzIGhlbHA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiYXJsZXkpICsKICAgIGdlb21fZGVuc2l0eV9yaWRnZXMoCiAgICAgICAgYWVzKHggPSB5aWVsZCwKICAgICAgICAgICAgeSA9IHNpdGUsCiAgICAgICAgICAgIGdyb3VwID0gaW50ZXJhY3Rpb24oeWVhciwgc2l0ZSksCiAgICAgICAgICAgIGZpbGwgPSB5ZWFyKSwKICAgICAgICBhbHBoYSA9IDAuOCkgKwogICAgeWxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpBZGp1c3RpbmcgdGhlIHZlcnRpY2FsIHNjYWxlIG1heSBhbHNvIGhlbHA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiYXJsZXkpICsKICAgIGdlb21fZGVuc2l0eV9yaWRnZXMoCiAgICAgICAgYWVzKHggPSB5aWVsZCwKICAgICAgICAgICAgeSA9IHNpdGUsCiAgICAgICAgICAgIGdyb3VwID0gaW50ZXJhY3Rpb24oeWVhciwgc2l0ZSksCiAgICAgICAgICAgIGZpbGwgPSB5ZWFyKSwKICAgICAgICBzY2FsZSA9IDAuOCkgKwogICAgeWxhYihOVUxMKSArCiAgICB0aG0KYGBgCgpTb21ldGltZXMgcmVvcmRlcmluZyB0aGUgZ3JvdXBpbmcgdmFyaWFibGUsIGB5ZWFyYCBpbiB0aGlzIGNhc2UsIGNhbgpoZWxwLgoKVGhlIGZhY3RvciBsZXZlbHMgb2YgYHllYXJgIGNhbiBiZSByZW9yZGVyZWQgdG8gbWF0Y2ggdGhlIG9yZGVyIG9mCmF2ZXJhZ2UgeWVhbGRzIHdpdGhpbiBlYWNoIHllYXIgYnkKCmBgYHtyLCBldmFsID0gRkFMU0V9CnJlb3JkZXIoeWVhciwgeWllbGQpCmBgYAoKVXNpbmcgYC15aWVsZGAgcHJvZHVjZXMgdGhlIHJldmVyc2Ugb3JkZXIuCgpgYGB7ciwgbWVzc2FnZSA9IEZBTFNFLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShkcGx5cikKZ2dwbG90KG11dGF0ZShiYXJsZXksIHllYXIgPSByZW9yZGVyKHllYXIsIC15aWVsZCkpKSArCiAgICBnZW9tX2RlbnNpdHlfcmlkZ2VzKGFlcyh4ID0geWllbGQsIHkgPSBzaXRlLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgZ3JvdXAgPSBpbnRlcmFjdGlvbih5ZWFyLCBzaXRlKSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgIGZpbGwgPSB5ZWFyKSwKICAgICAgICAgICAgICAgICAgICAgICAgc2NhbGUgPSAwLjgpICsKICAgIHlsYWIoTlVMTCkgKwogICAgdGhtCmBgYAoKV2l0aCBzb21lIHR1bmluZyByaWRnZWxpbmUgcGxvdHMgY2FuIHNjYWxlIHdlbGwgdG8gbWFueSBkaXN0cmlidXRpb25zLgpBbiBleGFtcGxlIGZyb20gW0NsYXVzIFdpbGtlJ3MgYm9va10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6Lyk6CgpUaGUgYGdncGxvdDJtb3ZpZXNgIHBhY2thZ2UgcHJvdmlkZXMgZGF0YSBmcm9tCltJTURCXShodHRwczovL2ltZGIuY29tLykgb24gYSBsYXJnZSBudW1iZXIgb2YgbW92aWVzLCBpbmNsdWRpbmcgdGhlaXIKbGVuZ3RocywgaW4gYSB0aWJibGUgYG1vdmllc2A6CgpgYGB7cn0KbGlicmFyeShnZ3Bsb3QybW92aWVzKQpkaW0obW92aWVzKQpoZWFkKG1vdmllcykKYGBgCgpBIHJpZGdlbGluZSBwbG90IG9mIHRoZSBtb3ZpZSBsZW5ndGhzIGZvciBlYWNoIHllYXI6CgpgYGB7ciwgbWVzc2FnZSA9IEZBTFNFLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShkcGx5cikKbXYxMiA8LSBmaWx0ZXIobW92aWVzLCB5ZWFyID4gMTkxMikKZ2dwbG90KG12MTIsIGFlcyh4ID0gbGVuZ3RoLCB5ID0geWVhciwgZ3JvdXAgPSB5ZWFyKSkgKwogICAgZ2VvbV9kZW5zaXR5X3JpZGdlcyhzY2FsZSA9IDEwLAogICAgICAgICAgICAgICAgICAgICAgICBsaW5ld2lkdGggPSAwLjI1LAogICAgICAgICAgICAgICAgICAgICAgICByZWxfbWluX2hlaWdodCA9IDAuMDMsCiAgICAgICAgICAgICAgICAgICAgICAgIG5hLnJtID0gVFJVRSkgKwogICAgc2NhbGVfeF9jb250aW51b3VzKGxpbWl0cyA9IGMoMCwgMjAwKSkgKwogICAgc2NhbGVfeV9yZXZlcnNlKGJyZWFrcyA9IGMoMjAwMCwgMTk4MCwgMTk2MCwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIDE5NDAsIDE5MjApKSArCiAgICB0aGVtZV9taW5pbWFsKCkKYGBgCgpUaGlzIHNob3dzIHRoYXQgc2luY2UgdGhlIGVhcmx5IDE5NjAncyBmZWF0dXJlIGZpbG0gbGVuZ3RocyBoYXZlCnN0YWJpbGl6ZWQgdG8gYSBkaXN0cmlidXRpb24gY2VudGVyZWQgYXJvdW5kIDkwIG1pbnV0ZXM6CgpBbm90aGVyIG5pY2UgZXhhbXBsZToKW0RXLU5PTUlOQVRFXShodHRwczovL2VuLndpa2lwZWRpYS5vcmcvd2lraS9OT01JTkFURV8lMjhzY2FsaW5nX21ldGhvZCUyOSkKc2NvcmVzIGZvciBtZWFzdXJpbmcgcG9saXRpY2FsIHBvc2l0aW9uIG9mIG1lbWJlcnMgb2YgY29uZ3Jlc3Mgb3Zlcgp0aGUgeWVhcnM6CgpgYGB7ciwgZWNobyA9IEZBTFNFLCBvdXQud2lkdGggPSAiNzAlIn0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJwb2xhcml6YXRpb24uanBlZyIpKQpgYGAKCltPcmlnaW5hbCBjb2RlXSggaHR0cDovL3JwdWJzLmNvbS9pYW5ybWNkb25hbGQvMjkzMzA0KSBieSBJYW4KTWNEb25hbGQ7IGFub3RoZXIgdmVyc2lvbiBpcyBwcm92aWRlZCBpbiBbQ2xhdXMgV2lsa2Uncwpib29rXShodHRwczovL2NsYXVzd2lsa2UuY29tL2RhdGF2aXovKS4KCgojIyBSZWFkaW5nCgpDaGFwdGVyIFtfVmlzdWFsaXppbmcgZGlzdHJpYnV0aW9uczogSGlzdG9ncmFtcyBhbmQgZGVuc2l0eQogIHBsb3RzX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6L2hpc3RvZ3JhbXMtZGVuc2l0eS1wbG90cy5odG1sKQogIGluIFtfRnVuZGFtZW50YWxzIG9mIERhdGEKICBWaXN1YWxpemF0aW9uX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6LykuCgpTZWN0aW9uIFtfSGlzdG9ncmFtcyBhbmQgZGVuc2l0eQpwbG90c19dKGh0dHBzOi8vc29jdml6LmNvL2dyb3VwZmFjZXR0eC5odG1sI2hpc3RvZ3JhbXMpIGluIFtfRGF0YQpWaXN1YWxpemF0aW9uX10oaHR0cHM6Ly9zb2N2aXouY28vKS4KCkNoYXB0ZXIgW19WaXN1YWxpemluZyBkYXRhIGRpc3RyaWJ1dGlvbnNfXShodHRwczovL3JhZmFsYWIuZGZjaS5oYXJ2YXJkLmVkdS9kc2Jvb2stcGFydC0xL2RhdGF2aXovZGlzdHJpYnV0aW9ucy5odG1sKQppbiBbX0ludHJvZHVjdGlvbiB0byBEYXRhIFNjaWVuY2U6IERhdGEgQW5hbHlzaXMgYW5kIFByZWRpY3Rpb24KQWxnb3JpdGhtcyB3aXRoIFJfXShodHRwczovL3JhZmFsYWIuZGZjaS5oYXJ2YXJkLmVkdS9kc2Jvb2stcGFydC0xLykuCgoKIyMgSW50ZXJhY3RpdmUgVHV0b3JpYWwKCkFuIGludGVyYWN0aXZlIFtgbGVhcm5yYF0oaHR0cHM6Ly9yc3R1ZGlvLmdpdGh1Yi5pby9sZWFybnIvKSB0dXRvcmlhbApmb3IgdGhlc2Ugbm90ZXMgaXMgW2F2YWlsYWJsZV0oYHIgV0xOSygidHV0b3JpYWxzL2Rpc3RzLlJtZCIpYCkuCgpZb3UgY2FuIHJ1biB0aGUgdHV0b3JpYWwgd2l0aAoKYGBge3IsIGV2YWwgPSBGQUxTRX0KU1RBVDQ1ODA6OnJ1blR1dG9yaWFsKCJkaXN0cyIpCmBgYAoKWW91IGNhbiBpbnN0YWxsIHRoZSBjdXJyZW50IHZlcnNpb24gb2YgdGhlIGBTVEFUNDU4MGAgcGFja2FnZSB3aXRoCgpgYGB7ciwgZXZhbCA9IEZBTFNFfQpyZW1vdGVzOjppbnN0YWxsX2dpdGxhYigibHVrZS10aWVybmV5L1NUQVQ0NTgwIikKYGBgCgpZb3UgbWF5IG5lZWQgdG8gaW5zdGFsbCB0aGUgYHJlbW90ZXNgIHBhY2thZ2UgZnJvbSBDUkFOIGZpcnN0LgoKCiMjIEV4ZXJjaXNlcwoKMS4gQ29uc2lkZXIgdGhlIGNvZGUKCjwhLS0gIyMgbm9saW50IHN0YXJ0IC0tPgogICAgYGBge3IsIGV2YWwgPSBGQUxTRX0KICAgIGxpYnJhcnkoZ2dwbG90MikKICAgIGRhdGEoR2FsdG9uLCBwYWNrYWdlID0gIkhpc3REYXRhIikKICAgIGdncGxvdChHYWx0b24sIGFlcyh4ID0gcGFyZW50KSkgKwogICAgICAgIGdlb21faGlzdG9ncmFtKC0tLSwgZmlsbCA9ICJncmV5IiwgY29sb3IgPSAiYmxhY2siKQogICAgYGBgCjwhLS0gIyMgbm9saW50IGVuZCAtLT4KCiAgICBXaGljaCBvZiB0aGUgZm9sbG93aW5nIHJlcGxhY2VtZW50cyBmb3IgYC0tLWAgcHJvZHVjZXMgYSBoaXN0b2dyYW0KICAgIHdpdGggYmlucyB0aGF0IGFyZSBvbmUgaW5jaCB3aWRlIGFuZCBzdGFydCBhdCB3aG9sZSBpbnRlZ2Vycz8KICAgIAogICAgYS4gYGJpbndpZHRoID0gMWAKICAgIGIuIGBiaW53aWR0aCA9IDEsIGNlbnRlciA9IDY2LjVgCiAgICBjLiBgYmlud2lkdGggPSAyLCBjZW50ZXIgPSA2NmAKICAgIGQuIGBjZW50ZXIgPSA2NmAKCjIuIENvbnNpZGVyIHRoZSBjb2RlCgogICAgYGBge3IsIGV2YWwgPSBGQUxTRX0KICAgIGxpYnJhcnkoZ2dwbG90MikKICAgIGdncGxvdChmYWl0aGZ1bCwgYWVzKHggPSBlcnVwdGlvbnMpKSArIGdlb21fZGVuc2l0eSgtLS0pCiAgICBgYGAKICAgIAogICAgV2hpY2ggb2YgdGhlIGZvbGxvd2luZyByZXBsYWNlbWVudHMgZm9yIGAtLS1gIHByb2R1Y2VzIGEgZGVuc2l0eQogICAgcGxvdCB3aXRoIHRoZSBhcmVhIHVuZGVyIHRoZSBkZW5zaXR5IGluIGJsdWUgYW5kIG5vIGJsYWNrIGJvcmRlcj8KICAgIAogICAgYS4gYGNvbG9yID0gImxpZ2h0Ymx1ZSJgCiAgICBiLiBgZmlsbCA9ICJibGFjayIsIGNvbG9yID0gImxpZ2h0Ymx1ZSJgCiAgICBjLiBgZmlsbCA9ICJsaWdodGJsdWUiLCBjb2xvciA9IE5BYAogICAgZC4gYGZpbGwgPSBOQSwgY29sb3IgPSAiYmxhY2siYAoKMy4gQ29uc2lkZXIgdGhlIGNvZGUKCiAgICBgYGB7ciwgZXZhbCA9IEZBTFNFfQogICAgbGlicmFyeShnZ3Bsb3QyKQogICAgbGlicmFyeShnYXBtaW5kZXIpCiAgICBwIDwtIGdncGxvdChnYXBtaW5kZXIsIGFlcyh5ID0gY29udGluZW50LCB4ID0gbGlmZUV4cCkpCiAgICBgYGAKCiAgICBXaGljaCBvZiB0aGUgZm9sbG93aW5nIHByb2R1Y2VzIHZpb2xpbiBwbG90cyB3aXRob3V0IHRyaW1taW5nIGF0CiAgICB0aGUgc21hbGxlc3QgYW5kIGxhcmdlc3Qgb2JzZXJ2YXRpb25zLCBhbmQgaW5jbHVkaW5nIGEgbGluZSBhdCB0aGUKICAgIG1lZGlhbj8KCiAgICBhLiBgcCArIGdlb21fdmlvbGluKHRyaW0gPSBGQUxTRSlgCiAgICBiLiBgcCArIGdlb21fdmlvbGluKHRyaW0gPSBUUlVFLCBzaG93X21lZGlhbiA9IFRSVUUpYAogICAgYy4gYHAgKyBnZW9tX3Zpb2xpbih0cmltID0gRkFMU0UsIGRyYXdfcXVhbnRpbGVzID0gMC41KWAKICAgIGQuIGBwICsgZ2VvbV92aW9saW4odHJpbSA9IFRSVUUsIHNob3dfcXVhbnRpbGVzID0gMC41KWAKCjQuIERlbnNpdHkgcmlkZ2VzIGNhbiBhbHNvIHNob3cgcXVhbnRpbGVzLCBidXQgdGhlIGRldGFpbHMgb2YgaG93IHRvCiAgIHJlcXVlc3QgdGhpcyBhcmUgZGlmZmVyZW50LiBDb25zaWRlciB0aGlzIGNvZGU6CgogICAgYGBge3IsIGV2YWwgPSBGQUxTRX0KICAgIGxpYnJhcnkoZ2dwbG90MikKICAgIGxpYnJhcnkoZ2dyaWRnZXMpCiAgICBsaWJyYXJ5KGdhcG1pbmRlcikKICAgIGdncGxvdChnYXBtaW5kZXIsIGFlcyh4ID0gbGlmZUV4cCwgeSA9IHllYXIsIGdyb3VwID0geWVhcikpICsKICAgICAgICBnZW9tX2RlbnNpdHlfcmlkZ2VzKC0tLSkKICAgIGBgYAogICAgCiAgICBXaGljaCBvZiB0aGUgZm9sbG93aW5nIHJlcGxhY2VtZW50cyBmb3IgYC0tLWAgcHJvZHVjZXMgZGVuc2l0eQogICAgcmlkZ2VzIHdpdGggbGluZXMgc2hvd2luZyB0aGUgbG9jYXRpb25zIG9mIHRoZSBtZWRpYW5zPwogICAgCiAgICBhLiBgcXVhbnRpbGVzID0gMC41YAogICAgYi4gYHF1YW50aWxlX2xpbmVzID0gVFJVRSwgcXVhbnRpbGVzID0gMC41YAogICAgYy4gYHF1YW50aWxlX2xpbmVzID0gVFJVRWAKICAgIGQuIGBkcmF3X3F1YW50aWxlcyA9IDAuNWAKCjwhLS0KYm94cGxvdHMKdmlvbGluIHBsb3RzCgpwbyA8LSBmdW5jdGlvbihwcm9iLCBxdWFudCkgewogICAgcTI1IDwtIHF1YW50KDAuMjUpCiAgICBxNzUgPC0gcXVhbnQoMC43NSkKICAgIG1kIDwtIHF1YW50KDAuNSkKICAgIElRUiA8LSBxNzUgLSBxMjUKICAgIHVvcCA8LSBwcm9iKHE3NSArIDEuNSAqIElRUiwgbG93ZXIudGFpbCA9IEZBTFNFKQogICAgbG9wIDwtIHByb2IocTI1IC0gMS41ICogSVFSKQogICAgYyhsb3AsIHVvcCkKfQotLT4K