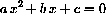
Chapter Summary
Complex numbers are an extension of the ordinary "real" numbers. The extended numbers allow us to solve all polynomial equations. These solutions are useful in calculus where complex exponentials give all solutions to linear differential equations.
Complex numbers first arise in solving polynomial equations.
For example, the quadratic equation
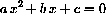
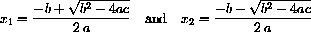
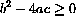
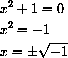
Complex numbers begin by defining a new number
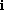 with the property that
with the property that
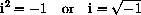
 and
and
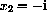 , because
, because
 and
and
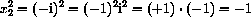 .
.
The quadratic roots above in the case where b2-4ac<0 can be written
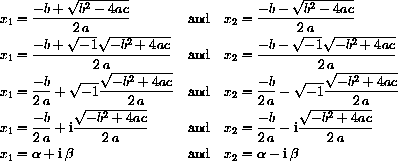
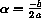 and
and
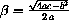 . Notice that the previous computation uses ordinary rules of algebra such as
. Notice that the previous computation uses ordinary rules of algebra such as
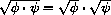 with
with
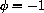 .
.
These computations lead us to the basic question, "What are the properties of the complex numbers?" This question is just another way to ask, "How do we compute with complex numbers?"
29.1
We begin with a useful formal definition of the "expression"
Example CD-29.1
Specific Addition and Multiplication
We usually will not use ordered pair notation when computing with complex numbers because the expression
Example CD-29.2
Complex Numbers as "Expressions in the Imaginary Unit"
It is helpful in doing algebra to use the "imaginary" symbol
Formal multiplication begins with the distributive law for
We equate the expressions
Example CD-29.3
Real Numbers as Complex Numbers with Zero Imaginary Part
Real numbers with their usual operations are included in the complex numbers as the ordered pairs
A complex number is zero only when both of its parts are zero, if
The properties that extend from real to complex algebra that we used in the formal computations with
The commutative laws of addition and multiplication,
A formal proof of this theorem amounts to writing out both sides of the identities above as ordered pairs and using properties of the real components to show they agree.
The importance of the result is that the procedure of computing with expressions
Each complex number
Each nonzero complex number
Complex division has the properties that if
PROOF:
For an additive inverse let
For a multiplicative inverse, multiply the numerator and denominator by the algebraic conjugate,
Exercise CD-29.1.5 asks you to show the properties above for the complex reciprocal.
Example CD-29.4
A Specific Reciprocal
We use the complex conjugate to make division real.
For example,
In the following examples we will write the polar forms of complex numbers using both trig functions and complex exponentials.
They are equal by Euler's formula, but the use of the exponential identity is sometimes clearer.
Example CD-29.10
Square Roots by Geometry
Suppose we want to find the square roots of
We seek the square root and its length squared must be 2, so the length of the square root is
There is another square root.
We can find it formally by representing the original number with another angle.
Example CD-29.11
Cube Roots by Geometry
Suppose we want to find the cube roots of
Two more cube roots could be obtained by dividing the angles in the polar representations
Example CD-29.12
Roots of Unity
Let n be a positive integer.
We seek all the solutions to zn=1 or
For example, if n=3,
The numbers
Finally, if
Section Summary
We define complex numbers and show that they have the "algebraic" properties of ordinary numbers. (They do not have the "order properties.") 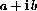 .
.
Definition: Complex Numbers Complex numbers are ordered pairs of real numbers (a,b) for any pair of real numbers a and b. The first component a is called the "real part" of (a,b) and the second component b is called the "imaginary part" of (a,b). Addition is defined componentwise,
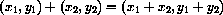
and complex multiplication is defined by
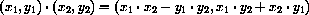
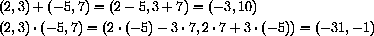
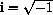 is more useful once we understand its computational properties.
The ordered pair definition is very clear and specific.
It allows us to prove Theroem CD-29.2 and justify the procedure we first illustrate with some examples as follows.
is more useful once we understand its computational properties.
The ordered pair definition is very clear and specific.
It allows us to prove Theroem CD-29.2 and justify the procedure we first illustrate with some examples as follows.
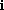 as the second place holder, so we also write complex numbers (a,b) as expressions of the form
as the second place holder, so we also write complex numbers (a,b) as expressions of the form
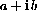 . Consider the previous examples as formal high school algebra computations just treating
. Consider the previous examples as formal high school algebra computations just treating
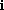 as a variable in an algebraic expression.
as a variable in an algebraic expression.

The formal sum computation first uses the associative law that says we can group addition parentheses any way we wish.
Next, the commutative law that says we can interchange the order of summation.
Then the distributive law
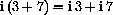 .
.
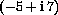 ,
, 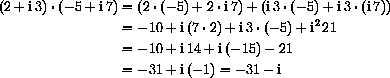
Next, the computation uses comutativity and associativity of multiplication,
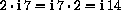 , etc.
The evaluation
, etc.
The evaluation
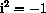 is an easy substitute for the ordered pair definition of complex multiplication above.
In general a complex product is computed with high school algebra as follows.
is an easy substitute for the ordered pair definition of complex multiplication above.
In general a complex product is computed with high school algebra as follows.
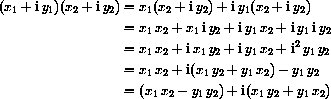
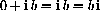 associated with the pair (0,b) and write
associated with the pair (0,b) and write
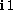 simply
simply
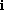 . If
. If
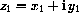 and
and
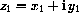 , then z1=z2 if and only if x1=x2 and y1=y2.
, then z1=z2 if and only if x1=x2 and y1=y2.
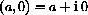 . In other words, the complex operations give the same results,
. In other words, the complex operations give the same results,
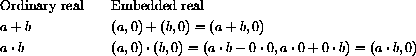
As a result of this extension, we write a complex number of the form
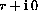 simply as r and treat a complex number with zero imaginary part as a real number.
In particular,
simply as r and treat a complex number with zero imaginary part as a real number.
In particular,
 and
and
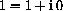 .
.
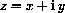 , then z=0 if and only if both x=0 and y=0.
, then z=0 if and only if both x=0 and y=0.
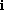 above are as follows.
above are as follows.
Theorem CD-29.1
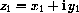 ,
, 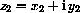 and
and
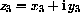 satisfy:
satisfy:
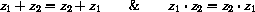
The associative laws of addition and multiplication,

The distributive law of multiplication over addition,

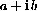 treating
treating
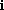 like an algebraic variable and simplifying with
like an algebraic variable and simplifying with
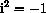 makes the computations correct.
makes the computations correct.
Theorem CD-29.2
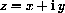 has an additive inverse, -z, with z+(-z)=0.
has an additive inverse, -z, with z+(-z)=0.
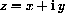 has a multiplicative inverse,
has a multiplicative inverse,
 , with
, with
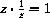 .
.
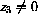 and
and
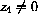 , then
, then
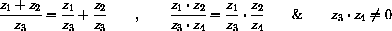
 then
then
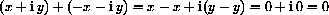 .
.
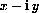 ,
, 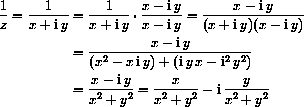
Exercise CD-29.1.2 asks you to compute the product
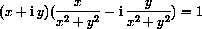
proving that this is the reciprocal.
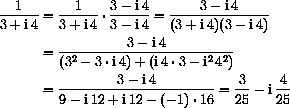
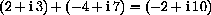
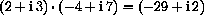
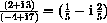
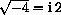
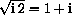 (HINT: See the next part of the exercise.)
(HINT: See the next part of the exercise.) 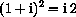
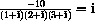
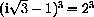
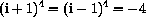
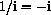 Check your work with the program CmplxNrs.
Check your work with the program CmplxNrs. 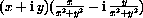 , showing that
, showing that
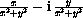 is the reciprocal of
is the reciprocal of
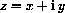 . Where do you require that
. Where do you require that
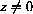 ?
?
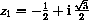 and
and
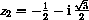 both satisfy z2+z+1=0 and z3=1.
both satisfy z2+z+1=0 and z3=1.
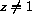 , show that
, show that
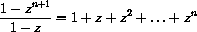
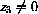 and
and
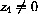 , then
, then
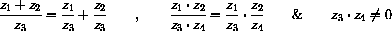

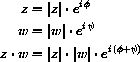
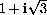 . These components lie on a triangle with sides 1,
. These components lie on a triangle with sides 1, 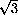 and hypotenuse 2, a "30-60-90" triangle.
This makes the direction angle from the x-axis 60 degrees or
and hypotenuse 2, a "30-60-90" triangle.
This makes the direction angle from the x-axis 60 degrees or
 . The length of the vector is 2.
. The length of the vector is 2.
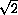 . The angle of the square root is half the angle
. The angle of the square root is half the angle
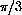 of the original number because we multiply the square root times itself, adding its angle to itself, and must arrive at
of the original number because we multiply the square root times itself, adding its angle to itself, and must arrive at
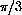 .
. 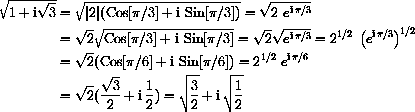
Notice that division of the angle by 2 agrees with the laws of exponents when the polar form is written with Euler's Formula.
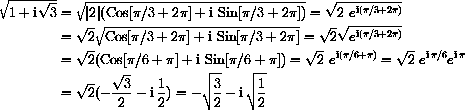
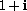 . In this case the length is
. In this case the length is
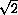 and the angle is 45 degrees, so
and the angle is 45 degrees, so
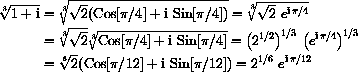
but the sine and cosine do not have simple values.
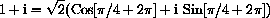
and
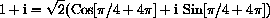
All the cube roots can also be obtained from one of them and the 3 cube roots of unity.
We describe this approach next.
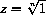 . The real solution z=1 is one possibility, but there are n-1 others equally distributed around the unit circle.
We can represent
. The real solution z=1 is one possibility, but there are n-1 others equally distributed around the unit circle.
We can represent
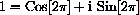 . Dividing this angle by n gives us
. Dividing this angle by n gives us

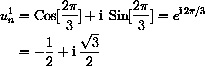
the point one third of the way around the unit circle.
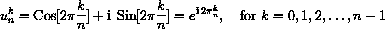
are equally spaced around the unit circle and satisfy (unk)n=1 because n times the angles
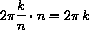 and
and
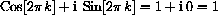 .
.
 is one nth root of z,
is one nth root of z, 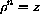
Then the numbers
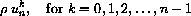
also satisfy
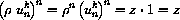
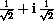
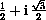
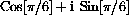
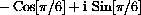
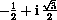
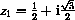 and
and
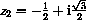
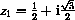 and
and
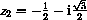
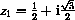 and
and
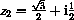
 and
and
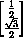 .
.
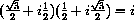 . (
. (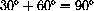 )
) 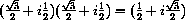 . (
. (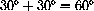 )
)
 and
and
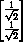 .
.
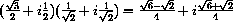
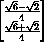 and show that it makes an angle of
and show that it makes an angle of
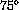 with the horizontal. (
with the horizontal. (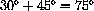 )
)
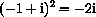
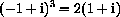
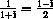

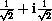 ,
, 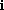 ,
, 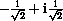 , -1,
, -1, 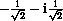 ,
, 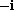 , and
, and
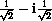 are eight distinct eighth roots of unity.
HINT: Draw them on the unit circle and show that they are equally spaced.
are eight distinct eighth roots of unity.
HINT: Draw them on the unit circle and show that they are equally spaced.
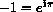 and sketch them on the unit circle.
and sketch them on the unit circle.
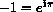 and sketch them on the unit circle.
and sketch them on the unit circle.
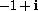 and sketch them on the unit circle.
and sketch them on the unit circle. 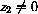 , then
, then
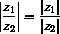 .
.