13.2
13.3
13.4
13.5
Use the change of variable
Use the change of variable
A triangle is shown in Figure CD-13.2 for a change of variable
A triangle is shown in Figure CD-13.2 for a change of variable
We are beginning to wallow a little too deeply in trig.
The point of the previous example could simply be: change the limits of integration when you change variable and differential.
However, it is possible to change back to u, and the previous exercise gives you a start on the trig skills needed to do this.
Problem CD-13.1
A Constant
Is
13.7
13.8
13.5.1
Combining these facts we have,
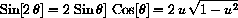
and

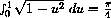
Sketch the graph
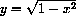 for
for
 . What geometrical shape is shown in your graph? What is the area of one fourth of a circle of unit radius?
. What geometrical shape is shown in your graph? What is the area of one fourth of a circle of unit radius?
 . (Check your symbolic computation geometrically).
. (Check your symbolic computation geometrically).
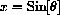 with an appropriate differential to show that
with an appropriate differential to show that

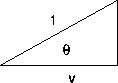
How large can we take v?
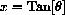 with an appropriate differential to show that
with an appropriate differential to show that
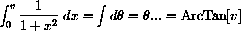
How large can we take v?
Suppose we make the change of variable
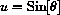 (as in the integration above). Express
(as in the integration above). Express
 in terms of u by using Figure CD-13.1 and TOA.
in terms of u by using Figure CD-13.1 and TOA.
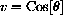 . Express
. Express
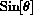 and
and
 in terms of v by using the figure and the Pythagorean Theorem.
in terms of v by using the figure and the Pythagorean Theorem.
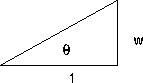
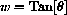 . Express
. Express
 and
and
 in terms of w by using the figure and the Pythagorean Theorem.
in terms of w by using the figure and the Pythagorean Theorem.
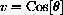 = CAH and
= CAH and
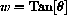 = TOA
= TOA
Use the change of variable
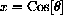 with an appropriate differential to show that
with an appropriate differential to show that
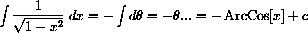
Also, use the change of variable
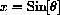 with an appropriate differential to show that
with an appropriate differential to show that
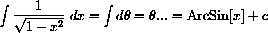
 ? Ask the computer to Plot
? Ask the computer to Plot
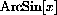 and
and
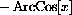 . Why do they look alike? How do they differ? Do the graphs of
. Why do they look alike? How do they differ? Do the graphs of
 and
and
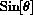 look alike? How do they differ?
look alike? How do they differ?
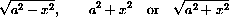
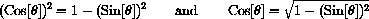


 , so, when the cosine is positive,
, so, when the cosine is positive,
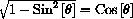 and
and

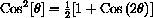 , so
, so
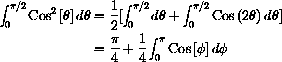
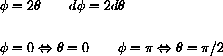
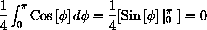
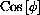 from 0 to
from 0 to
 , with equal areas above and below the
, with equal areas above and below the
 -axis.
-axis.
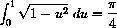

 when we let
when we let
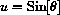 . There is an important algebraic detail when we write
. There is an important algebraic detail when we write
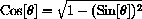
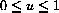 and chose
and chose
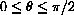 to put
to put
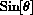 in this range.
It is also true that
in this range.
It is also true that
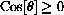 for this range of
for this range of
 , so that
, so that
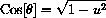
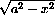 can first be reduced to a multiple of
can first be reduced to a multiple of
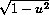 by taking u=x/a and writing
by taking u=x/a and writing
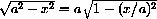 . This means that the expression
. This means that the expression
 with the substitutions u=(x/a)2 and
with the substitutions u=(x/a)2 and
 (provided cosine is positive on the interval).
(provided cosine is positive on the interval).
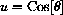 converts
converts
 into
into
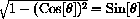 , provided sine is positive.
Also note that sine is positive over a different range of angles than cosine.
, provided sine is positive.
Also note that sine is positive over a different range of angles than cosine.
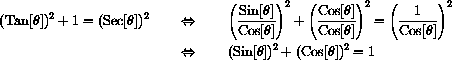
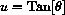 , then u2+1 becomes
, then u2+1 becomes
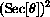 and
and
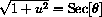 provided secant is positive.
provided secant is positive.
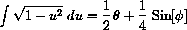
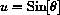 and
and
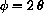 . If we really want the antiderivative of
. If we really want the antiderivative of
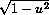 , then we must express all this in terms of u.
, then we must express all this in terms of u.

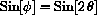 must first be written in terms of functions of
must first be written in terms of functions of
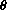 , (recall the addition formula for sine),
, (recall the addition formula for sine), 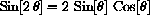
 idea.
From SOH-CAH-TOA, if we take a right triangle with hypotenuse 1 and opposite side u, then
idea.
From SOH-CAH-TOA, if we take a right triangle with hypotenuse 1 and opposite side u, then
 is the adjacent side of this triangle.
Using the Pythagorean Theorem, we have
is the adjacent side of this triangle.
Using the Pythagorean Theorem, we have
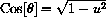
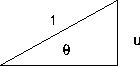
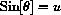 and
and
