24.2
24.3
24.4
Section Summary
Energy is a very important example of a general mathematical idea associated with dynamical systems, an invariant quantity. We also used an invariant of the SIR equations in Chapter 2 to find the limit of the susceptible population in an epidemic. This section studies invariants more carefully.
The energy
in an undamped spring
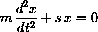
is constant. If it is moving, it has kinetic energy dependent on the mass; whereas, if the spring is compressed or extended, it has potential energy captured in the spring. As the system oscillates, it trades potential and kinetic energy forth and back between these two things, keeping the sum constant.
The energy in the damped spring
dissipates as a result of the shock absorber friction term
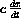. In this case, we can show that the analytical expression for energy is a decreasing quantity.
Because the level sets of the energy function are ellipses, we know that the flow of the dynamical system must steadily move inside smaller and smaller ellipses and thus approach a stable equilibrium at zero.
We already know stability in this case from explicit solutions, but the new approach via energy or a decreasing quantity is new and can apply to nonlinear systems when we do not know explicit solutions.
The undamped spring
Perhaps these steps are illegal, so let us build an interpretation of this calculation.
We will show that any solution of the dynamical system (x[t],y[t]) makes
The expression
What if we add damping
Calculate an invariant for the Lotka-Volterra model and plot the contours of that invariant using the the computer ContourPlot function.
Why are the orbits of the model closed loops as shown Figure CD-24.2?
24.5
24.4.1
can be written as the two-dimensional system
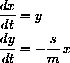
Without worrying about why this might work, divide the two equations and cancel dt 
Separate variables and integrate
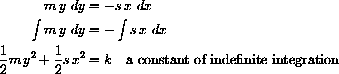
To prove that the quantity
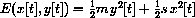is constant, it suffices to prove that its derivative is zero.
Differentiate and use the differential equations
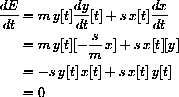
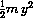is the kinetic energy and
is the potential energy.
We have just proved mathematically that the model conserves energy or that E is constant on solutions.
Another way to say this is that energy is an invariant of the dynamical system.
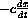and ask what happens to energy? Our differential equations are now
We will show that energy is decreasing by showing that
on solutions.
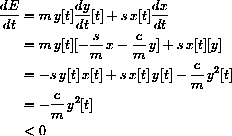
The level sets of E are shown in Figure CD-24.1 with lower levels corresponding to smaller ellipses - hence, solutions move into smaller and smaller ellipses.
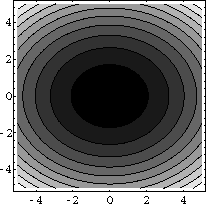
Figure CD-24.1: Constant energy
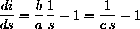
and integrating both sides to obtain
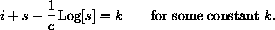
is constant for any solution (s[t],i[t]).
The Lotka-Volterra predator-prey equations are
for positive constants.
The sketch of the phase plane you did in Exercise CD-22.4.1 or the FoxRabbit example in the Flow2D program suggests closed loops in the flow.
The computer animation shows solutions that at least are very nearly closed loops.
Closed loop solutions have the ecological interpretation of persistent oscillations in the populations - years of boom and bust - for a population disturbed from equilibrium.
Figure CD-24.2: Lotka-Volterra invariant levels
24.5.1
24.5.2
24.5.3
24.5.4
24.5.5
24.5.6