22C:21: Computer Science II: Data Structures
Problem Set 5. Posted 2/16
Notes: Of the three problems given below, one will be solved by the
TAs in next week's discussion section, you will have to solve one in class,
and the remaining problem is due in the lecture on Friday, 2/24.
-
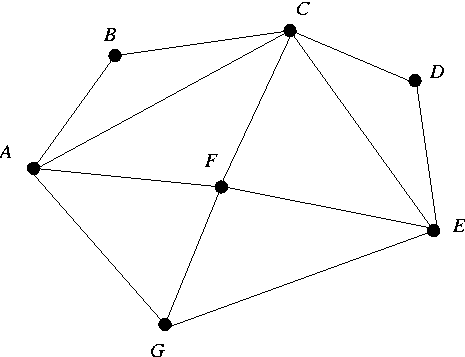
Show the adjacency matrix representation for the graph shown
below. Specifically, show the contents of the 1-dimensional array of
vertex names and the 2-dimensional boolean array that keeps track of the edges.
You should consult this Graph class for more
details.
Just so that all answers are consistent, I want you to store the names of
the vertices in alphabetical order in the array of vertex names.
Also, show what happens when you delete vertex C.
Specifically, show the new 1-dimensional array of names and
2-dimensional boolean array of edges after vertex C has been deleted.
-
Using this implementation of the Graph class,
I want you to write a program that builds a graph called the
Ladders graph.
Later we will use the Ladders graph to play the Ladders game.
In this two-player game, one player chooses a starting word and an ending
word and the other player constructs a "ladder" between the two words.
A ladder is a sequence of words that starts at the starting word, ends
at the ending word, and each word in the sequence (except the first) is
obtained from the previous word by changing a letter in a single position.
For example, suppose the starting word is flour and the
ending word is bread, then a ladder between these two
words is: flour, floor, flood,
blood, brood, broad, bread.
Here is the link that will take you to a file
called words.dat
that contains 5757 five letter English words.
This word list comes from Stanford Graphbase, a collection of
interesting data sets and graph algorithms put together by Donald E. Knuth.
The original file can be found here.
This word list is the database that your program will use to construct the
Ladders graph.
The Ladders graph should contain a vertex for every word in the file
and an edge between every pair of vertices that differ in exactly one
position.
To construct the graph, you should call the function addVertex
on every word in the file and then the function addEdge for every
edge you want to add.
After you have constructed the Ladders graph, I want your program to answer
the following questions:
- What is a word with maximum number of neighbors? Output such
a word and all its neighbors.
- What is a word with fewest number of neighbors? Output such
a word and all its neighbors.
You will have to electronically submit this program in a file called
Ladders.java.
I will open a directory called homework5 for this purpose.
There is no need to submit the Graph class.
-
Notice that in the deleteVertex function there is no attempt
to "shrink" the 1-dimensional array of names or the 2-dimensional
array of edges, when a vertex leaves.
This may lead to the possibility that we are using up far more space
than necessary, for the graph.
Modify deleteVertex so that it shrinks the
1-dimensional array of names and the 2-dimensional
array of edges, when a vertex leaves.
Of course, it would be quite inefficient to do this every time
a vertex leaves.
So we would do it only when the number of vertics falls to less
than half the size of the 1-dimensional array of names.

