22C:21: Computer Science II: Data Structures
Project 2. Posted 10/29. Due 11/15
Introduction
This project mainly consists of three, fairly independent parts.
These parts will involve modifying the myListGraph
class and the City class.
- Modify the myListGraph class
so that it can represent edge-weighted graphs and modify the
City class so that it can make edge-weighte
graphs.
- Add TSP methods to the edge-weighted graph class.
- Add a method to compute a minimum spanning tree to the
edge-weighted graph class.
After these three tasks have been performed, you will have to perform
experiments that involve building minimum spanning trees and travelling
salesman tours using selected cities and selected edges.
As in the case of Project 1, your data comes from the file
miles.dat.
The myWeightedGraph class
Starting from myListGraph, construct a class called
myWeightedGraph that allows to to store and manipulate edge-weighted graphs.
We will assume that edge weights are real numbers.
The unweighted graphs we have been dealing with thus far can be viewed as graphs in which
each edge has weight 1.0.
To be able to store edge weights, we have to modify the adjacency list representation
just a bit.
Details of how this should be done are discussed in the Lab 10 document.
Some code has also been provided to help you get started.
The myWeightedGraph class needs to have a few extra methods that allow the user
to deal with edge weights.
- The method addEdge should now have two versions
void addEdge(String u, String v)
void addEdge(String u, String v, double w)
The second version adds an edge {u, v} of weight w to the graph. The first version
adds an edge {u, v} with the default weight of 1.0.
- Two versions of a new method
Double getWeight(String u, String v)
Double getWeight(int i, int j)
should be added. The first version takes two vertices u and v and
returns the weight of the edge connecting them. It is possible that u and v
are not neighbors and in this case the function should return null. To make
this possible, I have set the return type of the function to Double instead
of double.
TSP methods
Add methods to the myWeightedGraph class that compute a traveling
salesman's tour of this graph.
Note that these methods are not in the City class, but in the
myWeightedGraph class.
Add the versions of the TSP method, given below.
- String[] GreedyTSP(String v): This function returns
a traveling saleman's tour starting from the vertex v. The tour
is just a sequence of vertex names and is therefore returned as a
String[]. The tour is computed by using the greedy algorithm
described in homework 8.
- String[] BruteForceTSP(String v): This function is like the
above function, except that it uses the "search with backtracking" algorithm
described in homework 8.
- String[] GreedyTSP(): This is like the first function except
that it starts the tour at an arbitrary vertex.
- String[] BruteForceTSP(): This function is like the second
function except that it starts the tour at an arbitrary vertex.
A few remarks about these methods are in order.
-
That we are providing separate GreedyTSP and BruteForceTSP
methods allows the user a choice: does she want a pretty good, but not
optimal traveling salesman's tour quickly or is she willing to wait
for a long time to get an optimal traveling salesman's tour?
-
Also note that a traveling salesman's tour is only allowed to use those
edges that exist (and not all possible edges between pairs of cities
may exist). This means that the TSP method that you are implementing
for homework 8 needs to be modified slightly for
the project. For example, in the recursive case of the pseudocode
we attempt to extend the partial tour R by considering each
city c not in R. This has to be modifed to consider
only those cities c, not in R, that are neighbors of
the last city in R.
-
Also note that if this graph has several connected components then
the traveling salesman tour will just visit one of the connected
components.
Computing a Minimum Spanning Tree:
Let G be a connected, edge-weighted graph.
A minimum spanning tree of G is a subgraph of G that is
satisfies the following properties:
- It is a tree, that is, it is connected and has no cyles.
- It is spanning, that is, it contains all vertices of G.
- It has minimum total edge-weight among all possible trees.
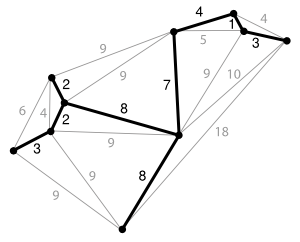 For example, the above picture shows an edge-weighted graph along with its minimum spanning tree
(made up of the thick edges).
Notice that the graph made up of the thick edges is indeed a tree (it is connected and
has no cycles) and it is spanning (has all vertices in it).
It is just a bit harder to verify that it is also a spanning tree with smallest possible weight
(3 + 2 + 2 + 8 + 8 + 7 + 4 + 1 + 3 = 37).
As you can imagine, minimum spanning trees are very important to telephone companies,
cable companies, transportation companies, etc.
For example, the above picture shows an edge-weighted graph along with its minimum spanning tree
(made up of the thick edges).
Notice that the graph made up of the thick edges is indeed a tree (it is connected and
has no cycles) and it is spanning (has all vertices in it).
It is just a bit harder to verify that it is also a spanning tree with smallest possible weight
(3 + 2 + 2 + 8 + 8 + 7 + 4 + 1 + 3 = 37).
As you can imagine, minimum spanning trees are very important to telephone companies,
cable companies, transportation companies, etc.
Algorithms for computing a minimum spanning tree have been around for a long time and
here I will describe an algorithm known as
Prim's Algorithm.
The nice thing about minimum spanning trees is that a greedy strategy works for computing these.
Prim's algorithm starts with an arbitrary vertex, let us call this s.
At this point imagine that we have a tree just containing the vertex s.
The algorithm performs a "greedy" step repeatedly, growing the tree by one vertex in each
repitition of the greedy step.
Let S be the set of vertices in the current tree. If S is not the set of all
vertices, then the tree is grown by adding a vertex u and an edge {u, v}
to the tree where u is outside of S and {u, v}
is the edge with smallest weight that connects a vertex in S to a vertex
outside S.
In this way the tree would grow by one vertex in each step and the algorithm would terminate
when all vertices are included in the tree.
There is a nice example here showing
Prim's algorithm in action.
Prim's algorithm can be expressed quite simply in the following pseudocode.
Pick an arbitrary vertex s;
Mark s visited;
Repeat n-1 times
{
Let {u, v} be an edge with smallest weight among all edges of
the kind in which u is a visited vertex and v is not;
Mark v visited;
Add {u, v} to the tree;
}
Add the following methods to the myWeightedGraph class to compute a minimum
spanning tree of this graph.
- int[] MST(): This methods computes a minimum spanning tree and
returns it as tree rooted at the starting vertex s.
As we saw in the context of breadth-first search, such a tree can be represented
in an int[] by just keeping track of the parent pointers.
- myWeightedGraph MST(): This method computes a minimum spanning tree and
returns it as an edge-weighted graph.
- double costMST(): This method returns the total weight of a minimum spanning tree.
Experiments:
To test your implementation, write code to answer the following questions.
Place this code in programs called CityTester1.java, CityTester2.java,
CityTester3.java, and
CityTester4.java.
- What is the cheapest traveling salesman tour you can compute of
the set of all cities?
As you know from an earlier homework, computing an optimal tour of 128
cities may take too long, and so using the greedy algorithm may be
the best approach.
- What is an optimal traveling salesman tour of the cities in the upper
midwest (i.e., between latitudes 40 N and 50 N and longitudes 85 W and 100 W)?
- What is a minimum spanning tree of the cities in the upper midwest?
Print out all the edges this minimum spanning tree and also print out its cost.
- An airline company decides to create "hubs" in all cities (in the data set)
with population at least 200,000. It decides to fly all routes in a minimum spanning
tree of the hubs. In addition, it decides to fly routes the connect each of the remaining
cities to the nearest hub. Enumerate all the routes that the airline company
will fly. Also, print out (i) the average number of routes that visit a city
(the average being taken over all cities) and (ii) the average number of hops
between a source and a destination (with the average being taken over all
source destination pairs).
What to submit:
Submit your java programs: City.java, myWeightedEdgeGraph.java,
CityTester1.java, CityTester2.java,
CityTester3.java, and
CityTester4.java.
In addition you should submit City.readme.
As usual this should mention all known errors, gross inefficiencies,
all required methods that are unimplemented, and documentation for
all "extra" methods that were implemented.
Also, submit Project2.pdf; this should describe the answers you
got from running the four experiments.

