Depth-first search is a graph traversal that is algorithmically similar to breadth-first search, but ends up visiting vertices in an order very different from breadth-first search. The basic idea for depth-first search is the following. Start from the source vertex by marking it visited and then visit an arbitrary unvisited neighbor, say x. Then repeat the process from x. Keep doing this until we get to a vertex, say y, that has no unvisited neighors. Vertex y is said to be a dead end. On reaching a dead end, the algorithm "backtracks" to the parent of y and tries to find an unvisited neighbor of the parent. The process continues until the algorithm backtracks all the way back to the source and the source has no unvisited neighbors.
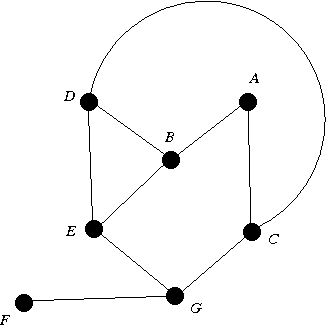
As an illustration, consider a depth-first search of the graph given below,
starting with source A.
To make the illustration concrete, let us assume that neighbors of each vertex
are scanned in alphabetical order.

Vertices in the order parent visited A A B A D B C D G C E (dead end) G F (dead end) GNote that by the time vertex F is visited, all vertices have been visited. Then the algorithm backtracks from vertex F back to G, then back to C, then back to D, then back to B, then back to A, where it stops.
Just like breadth-first search was implemented using a Queue ADT, depth-first search can be implemented by using a Stack ADT. Here is the pseudo-code:
depthFirstSearch(source){
//Initialization
mark source visited
Define an empty stack S
S.push(source)
// Main loop
while(S is not empty){
currentVertex <- S.pop()
Scan the neighbors of currentVertex, looking for an unvisited neighbor
if an unvisited neighbor (called x) is found then{
S.push(currentVertex)
S.push(x)
} // end of if
} // end of main while-loop
} // end of function
The stack plays a critical role in allowing the depth-first search algorithm to backtrack. Specifically, the stack always stores the current path, i.e., a path from the source to currentVertex, with source at the bottom of the stack and currentVertex at the top of the stack. If we find an unvisited neighbor x of currentVertex, then x is pushed onto the stack and is sitting on top of currentVertex, thereby extending the current path to x. Otherwise, if currentVertex is a dead end, then it is popped from the stack and we end up with the parent of currentVertex sitting on top of the stack.
As an illustration, here are the contents of the stack at the beginning of each iteration of the while-loop in the above pseudocode.
bottom top A A B A B D A B D C A B D C G A B D C G E A B D C G A B D C G F A B D C G A B D C A B D A B A empty stack
Add an implementation of a method called depthFirstSearch to myListGraph.java. Use the following function header:
void depthFirstSearch(String source)As this is your first attempt at implementing depthFirstSearch, the only thing expected of this method is that it output each vertex, the first time it is visited. This will tell us the order in which vertices are visited by depth-first search. Use the Stack ADT implemented in myStack.java. Depth-first search, like breadth-first search is guaranteed to visit every vertex in the connected component containing the source vertex. To test your implementation, construct a program called depthFirstSearchTester.java that (i) constructs the Ladders graph and (ii) calls depthFirstSearch first with source vertex "alert," then with source vertex "debug," and then with source vertex "jiffy." These words belong to connected components of sizes 15, 15, and 24 respectively (as you can verify from allConnectedComponents.out). By comparing the output of depthFirstSearch with the words in each of these components, you can check the correctness of your implementation.
Submit myListGraph.java and depthFirstSearchTester.java.
Discussion. Like breadth-first search, depth-first search also has many applications (for e.g., in computing strongly connected components and biconnected components, and in topological sorting). Depth-first search can also be implemented in a natural way by using recursion. We will study that implementation in class, but if you are eager to see it right away, here it is.