This text developed out of our experiences teaching courses covering the formal semantics of programming languages. Independently we both developed laboratory exercises implementing small programming languages in Prolog following denotational definitions. Prolog proved to be an excellent tool for illustrating the formal semantics of programming languages. We found that these laboratory exercises were highly successful in motivating students. The hands-on experience helped demystify the learning of formal semantics. At a professional meeting we became aware of each other¹s experiences with this laboratory approach to semantics, and this book evolved from that conference.
Although this text has been carefully written so that the laboratory activities can be omitted without loss of continuity, we hope that most readers will try the laboratory approach and experience the same success that we have observed in our classes.
We have pursued a broad spectrum of definitional techniques, illustrated with numerous examples. Although the specification methods are formal, the presentation is ³gentle² providing just enough in the way of mathematical underpinnings to produce an understanding of the metalanguages. We hope to supply enough coverage of mathematics and formal methods to justify the definitional techniques, but the text is accessible to students with a basic grounding in discrete mathematics as presented to undergraduate computer science students.
There has been a tendency in the area of formal semantics to create cryptic, overly concise semantic definitions that intimidate students new to the study of programming languages. The emphasis in this text is on clear notational conventions with the goals of readability and understandability foremost in our minds.
As with other textbooks in this field, we introduce the basic concepts using mini-languages that are rich enough to illustrate the fundamental concepts yet sparse enough to avoid being overwhelming. We have named our mini-languages after birds.
Wren is a simple imperative language with two types, integer and boolean, thus allowing for context-sensitive type and declaration checking. It has assignment, if, while, and input/output commands.
Pelican, a block structured, imperative language, is an extension of Wren containing the declaration of constants, anonymous blocks, procedures, and recursive definitions.
The description of continuations in denotational semantics requires a modified version of Wren with goto statements, which we call Gull. This mini-language can be skipped without loss of continuity if continuations are not covered.
The primary target readership of our text is first-year graduate students, although by careful selection of materials it is also accessible to advanced undergraduate students. The text contains more material than can be covered in a one semester course. We have provided a wide variety of techniques so that instructors may choose materials to suit the particular needs of their students.
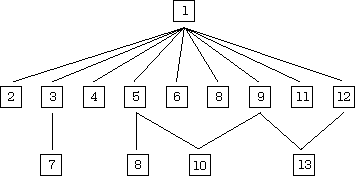
Dependencies between chapters are indicated in the graph below. We have purposely attempted to minimize mutual interdependencies and make our presentation as broad as possible.

Only sections 2 and 3 of Chapter 8 depend on Chapter 5 The text contains a laboratory component that we describe in more detail in a moment. However, materials have been carefully organized so that no components of the non-laboratory sections of the text are dependent on any laboratory activities. All of the laboratory activities except those in Chapter 6 depend on Chapter 2.
The first four chapters deal primarily with the syntax of programming languages. Chapter 1 treats context-free syntax in the guise of BNF grammars and their variants. Since most methods of semantic specification use abstract syntax trees, the abstract syntax of languages is presented and contrasted with concrete syntax.
Language processing with Prolog is introduced in Chapter 2 by describing a scanner for Wren and parser defined in terms of Prolog logic grammars. These utilities act as the front end for the prototype context checkers and interpreters developed later in the text. Extensions of BNF grammars that provide methods of verifying the context-sensitive aspects of programming languages‹namely, attribute grammars and two-level grammars‹are described in Chapters 3 and 4.
Chapters 5 through 8 are devoted to semantic formalisms that can be classified as operational semantics. Chapter 5 introduces the lambda calculus by describing its syntax and the evaluation of lambda expressions by reduction rules. Metacircular interpreters are consider in Chapter 6, which introduces the self-definition of programming languages.
Chapter 7 describes the translation of Wren into assembly language defined by an attribute grammar that constructs the target code as a program is parsed. Two well-known operational formalisms are treated in Chapter 8: the SECD machine, an abstract machine for evaluating the lambda calculus and structural operational semantics, an operational methodology for describing the semantics of programming languages in term of logical rules of inference. We use this technique to specity the semantics of Wren formally.
The last five chapters present three traditional methods of formally defining the semantics of programming languages and one recently proposed technique. Denotational semantics, one of the most complete and useful methods of specifying a programming language, is covered in Chapter 9. Specifications of several languages are provided, including a calculator language, Wren, Pelican, and Gull, a language whose semantics requires continuation semantics. Chapter 10 deals with the mathematical foundations of denotational semantics in domain theory by describing the data structures employed by denotational definitions. Chapter 10 also includes a justification for recursive definitions via fixed-point semantics.
Axiomatic semantics, dealt with in Chapter 11, has become an important component of software development by means of proofs of correctness for algorithms. The approach here presents axiomatic specifications of Wren and Pelican, but the primary examples involve proofs of correctness and termination. Chapter 12 investigates the algebraic of abstract data types and uses these formalisms to specify the context constraints and the semantics of Wren. Algebraic semantics also provides an explanation of abstract syntax. Chapter 13 introduces a specification method, action semantics, that has been proposed recently in response to the criticisms of the difficulty of using formal methods. Action semantics resembles denotational semantics but can be viewed in terms of operational behavior without sacrificing mathematical rigor. We use it to specify the semantics of the calculator language, Wren, and Pelican. The text concludes with two short appendices introducing the basics of programming in Prolog and Scheme, which is used in Chapter 6.
A unique feature of this text is the laboratory component. Running throughout the text is a series of exercises and examples that involve implementing syntactic and semantic specifications on real systems. We have chosen Prolog as the primary vehicle for these implementations for several reasons:
An appendix covering the basics of Prolog is provided for students unfamiliar with logic programming.
Our experience has shown that the laboratory practice greatly enhances the learning experience. The only way to master formal methods of language definition is to practice writing and reading language specifications. We involve students in the implementation of general tools that can be applied to a variety of examples and that provide increased motivation and feedback to the students. Submitting specifications to a prototyping system can uncover oversights and subtleties that are not apparent to a casual reader. As authors, we have frequently used these laboratory approaches to help debug our formal specifications!
Laboratory materials found in this textbook are available on the Internet via anonymous ftp from ftp.cs.uiowa.edu in the subdirectory pub/slonnegr.
Ken Slonneger
Barry L. Kurtz
 To Ken Slonneger's
Home Page
To Ken Slonneger's
Home Page