The
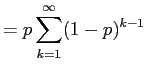 |
||
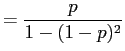 |
||
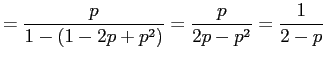 |
So if
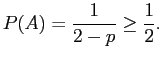 |
An alternative approach to deriving the formula for ![]() is to
condition on the results of the first two tosses. For the first
toss,
is to
condition on the results of the first two tosses. For the first
toss,
For the second toss
Since the tosses are independent, the game starts over if the first two tosses are tails, i.e.
So we have an equation in
and the solution is
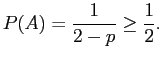 |
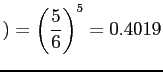 |
- a.
-
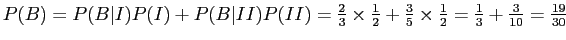
- b.
-
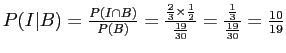
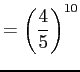 |
||
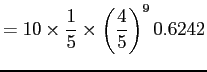 |
Therefore
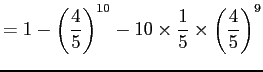 |
||
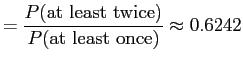 |
||
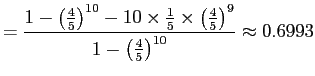 |
- (i)
-
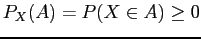 since
since 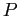 is a probability.
is a probability.
- (ii)
-
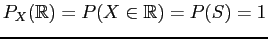 since
since 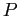 is a
probability.
is a
probability.
- (iii)
- For Borel sets
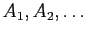 that are pairwise
disjoint,
that are pairwise
disjoint,
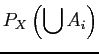
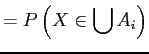
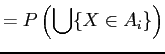
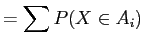
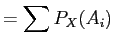
since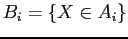 are pairwise disjoint.
are pairwise disjoint.
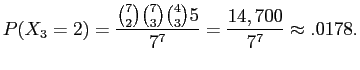 |
For
| Pattern | Ways | |
| 34 |
|
1,470 |
| 322 |
|
22,050 |
| 3211 |
|
176.400 |
| 31111 |
|
88,200 |
| 288,120 |
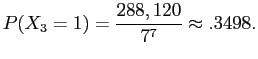 |
The remaining case can be handled by complementarity:
- (a)
- For all
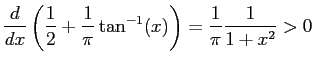
so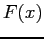 is increasing, and
is increasing, and
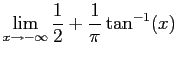
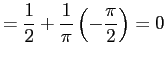
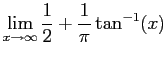
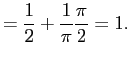
So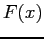 is a CDF.
is a CDF.
- (b)
- For all
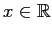
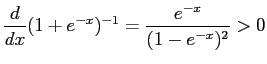
so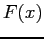 is increasing, and
is increasing, and
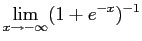
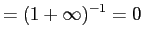
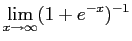
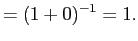
So is a CDF.
is a CDF.
- (c)
- For all
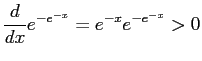
so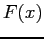 is increasing, and
is increasing, and
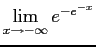
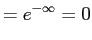
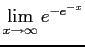
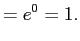
So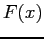 is a CDF.
is a CDF.
- (d)
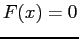 for
for 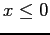 . For
. For 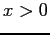
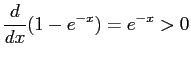
so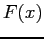 is nondecreasing, and
is nondecreasing, and
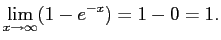
So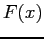 is a CDF.
is a CDF.
- (e)
- The function is continuous everywhere except possible at
the origin, and at the origin it is right continuous because of
the placement of the equality sign in the definition. The function
is increasing for
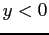 and for
and for 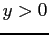 from part (b), and using
the limit results from part (b)
from part (b), and using
the limit results from part (b)
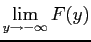
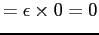
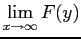
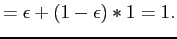
So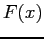 is a CDF.
is a CDF.
