- a.
-
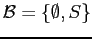 is a
is a 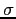 -algebra:
-algebra:
- (i)
-
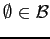 .
.
- (ii)
-
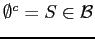 and
and
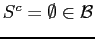 .
.
- (iii)
- Suppose
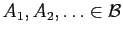 . If
. If
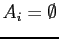 for all
for all 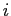 , then
, then
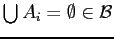 . If any
. If any
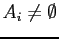 then it is
then it is  , and
, and
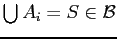 .
.
- b.
-
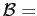 all subsets of $S$
all subsets of $S$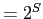 is a
is a
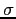 -algebra:
-algebra:
- (i)
 is a subset of
is a subset of 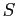 , so
, so
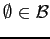 .
.
- (ii)
- If
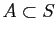 then
then
 , so
, so
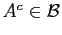 .
.
- (iii)
- If
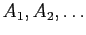 are subsets of
are subsets of 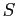 , then so
is
, then so
is
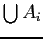 .
.
- c.
- Suppose
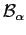 is a
is a 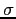 -algebra on
-algebra on 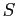 for
every
for
every 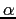 . Then
. Then
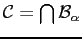 is a
is a
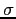 -algebra on
-algebra on 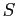 .
.
- (i)
- Since each
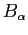 is a
is a 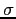 -algebra,
-algebra,
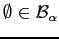 for all
for all 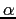 , so
, so
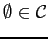 .
.
- (ii)
- If
 , then
, then
 for all
for all 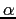 .
So
.
So
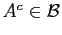 for all
for all 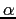 , i.e.
, i.e.
 .
.
- (iii)
- If
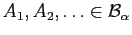 for all
for all
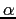 . then
. then
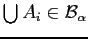 for all
for all
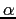 . So
. So
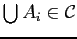 .
.
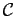 is a
is a 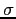 -algebra. This means ``smallest
-algebra. This means ``smallest
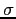 -algebra satisfying ...'' is well defined.
-algebra satisfying ...'' is well defined.
- a.
- Suppose
 and
and 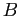 are disjoint. Let
are disjoint. Let
 ,
and
,
and
 for
for 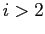 . Then, since
. Then, since
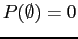 and the
and the 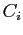 are pairwise disjoint,
are pairwise disjoint,


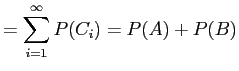
- b.
- Let
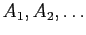 be pairwise disjoint. For each
be pairwise disjoint. For each
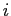 , let
, let
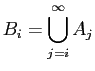
Then for each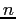 ,
,

Since are pairwise disjoint,
are pairwise disjoint,
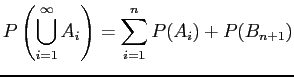
for every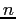 by finite additivity. But
by finite additivity. But
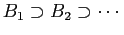
and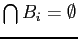 . So by continuity,
. So by continuity,
 . So
. So
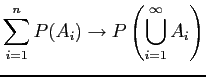
and thus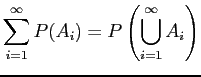
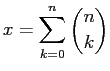 |
Can show
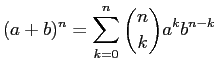 |
taking
Can also use a counting argument: Each subset corresponds to an
ordered list of ![]() 0's and 1's.
0's and 1's.
| if the |
||||
| if the |
For example, if
How many such lists are there?
- a.
- Two given plus sur:
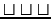 .
.  .
.
- b.
- One or two given plus sur:
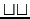 or
or
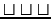 .
.
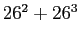 .
.
- c.
- One, two, or three given plus sur:
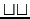 or
or
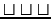 or
or
 .
.
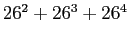 .
.
![]() has
has ![]() elements--repetition is allowed.
elements--repetition is allowed.
Assume equally likely outcomes. Equivalently, assume balls are assigned independently.
Exactly one cell empty means:
- one empty cell
- one with two
- n-2 with 1
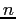 for the one empty cell
for the one empty cell
 for the cell with two balls
for the cell with two balls
-
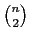 for the balls to use for the two-ball cell.
for the balls to use for the two-ball cell.
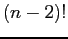 arrangements for the other balls in their cells.
arrangements for the other balls in their cells.
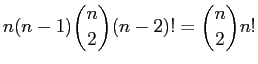 |
The probability of this arrangement is
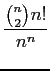 |
- select the day to be repeated--7 choices
- select the 6 calls to occur on that day--
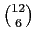 choices
choices
- assign the remaining 6 calls to the remaining 6 days--
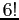 choices
choices
| Pattern | Count | |
| 6111111 |
|
4,656,960 |
| 5211111 |
|
83,825,280 |
| 4221111 |
|
523,908,000 |
| 4311111 |
|
139,708,800 |
| 3321111 |
|
139,708,800 |
| 3222111 |
|
1,397,088,000 |
| 2222211 |
|
314,344,800 |
| 3,162,075,840 |
A simpler alternative is to use the union-intersection formula. Let
![]() be the event that there are no calls on day
be the event that there are no calls on day ![]() . The event
that there is at least one call each day is then
. The event
that there is at least one call each day is then
![]() , and the complement of this event is
, and the complement of this event is
![]() . For any particular
. For any particular ![]() days
days
![]()
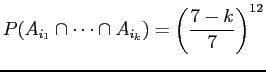 |
and there are
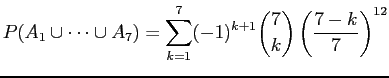 |
The last term is zero and can be dropped, so
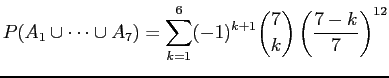 |
The number of ways to assign calls to days with each day receiving at least one call is therefore
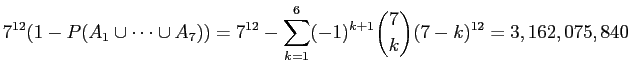 |
and the corresponding probability is
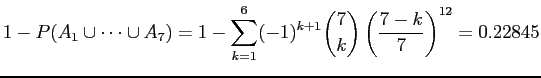 |
 |
Number of unordered selections:
 |
So the probability of no matching pair is
 |
Or: Choose pair for each shoe in
