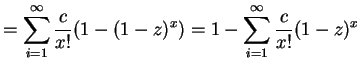 |
||
![$\displaystyle = 1-c\sum_{i=1}^{\infty}\frac{(1-z)^{x}}{x!} = 1-c\left[\sum_{i=0}^{\infty}\frac{(1-z)^{x}}{x!}-1\right]$](img786.png) |
||
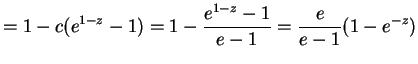 |
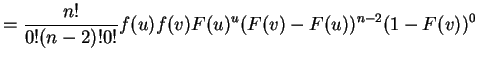 |
||
Let
The range of
The Jacobian determinant is
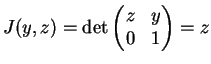 |
So for
Thus
This proof first removes ![]() from consideration since it is
just a scale parameter. An alternative approach is to note that
from consideration since it is
just a scale parameter. An alternative approach is to note that
![]() is sufficient,
is sufficient,
![]() is ancillary, and use
Basu's theorem in chapter 6.
is ancillary, and use
Basu's theorem in chapter 6.
- a.
- Suppose
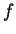 is continuous at
is continuous at 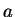 and
and
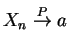 ,
, 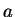 a constant. Fix
a constant. Fix
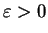 . Then there exists a
. Then there exists a
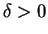 such that
such that
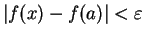
if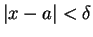 . So
. So

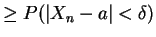

So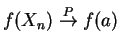 . The result follows if
. The result follows if
 or
or
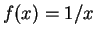 and
and 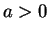 .
.
- b.
-
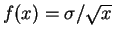 is continuous at
is continuous at
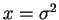 if
if
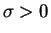 .
.
- a.
- For any
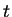 and any
and any
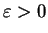 , if
, if 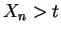 and
and
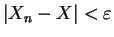 , then
, then
 . So
. So
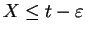 implies that either
implies that either 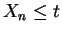 or
or
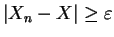 , i.e.
, i.e.

So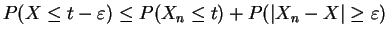
or
- b.
- Similarly (reversing the roles of
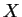 and
and 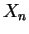 and
replacing
and
replacing 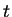 by
by
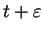 ),
),

- c.
- Suppose the CDF of
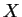 is continous at
is continous at 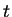 . From the
previous two parts, since
. From the
previous two parts, since
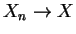 in probability we
have
in probability we
have
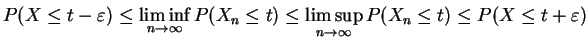
for any . Since
. Since 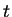 is a coninuity point of the
distribution of
is a coninuity point of the
distribution of 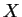 ,
,
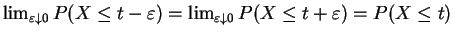 , and therefore
, and therefore
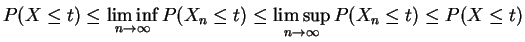
So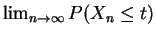 exists and is equal
to
exists and is equal
to
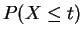 . Thus
. Thus
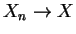 in distribution.
in distribution.
