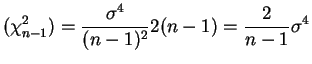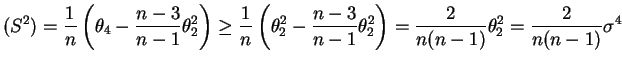Next: Assignment 13
Up: 22S:193 Statistical Inference I
Previous: Assignment 12
- 5.8
- a.
-
- b.
- Assume, without loss of generality, that
![$ E[X_{i}]=\theta_{1}=0$](img701.png) . Then
. Then
and
If 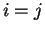 or
or 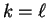 , then
, then
![$ E[(X_{i}-X_{j})^{2}(X_{k}-X_{\ell})^{2}]=0$](img706.png) . If all
. If all
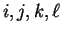 are different, then
are different, then
If
 , say
, say 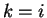 , then
, then
If
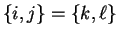 , then
, then
So
So
- c.
- Still assume
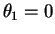 .
.
So
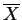 and
and  are uncorrelated if and only if
are uncorrelated if and only if
 .
.
- 5.10
- If
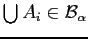 is odd,
is odd,
If 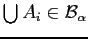 is even,
is even,
Let 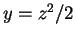 ,
,
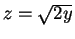 ,
,
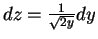 . So
. So
Now
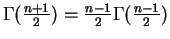 ,
So for even
,
So for even 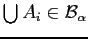 ,
,
and
if
 . So for
. So for
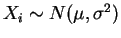
and
Using
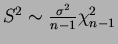 ,
,
Var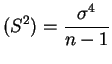 Var Var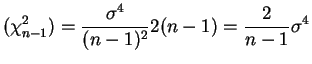 |
|
- 5.11
- This follows either from Jensen's inequality or from the
fact that
![$ E[S^2] - E[S]^2 =$](img770.png) Var
Var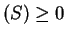 and thus
and thus
![$ E[S] \le
\sqrt{E[S^2]} = \sigma$](img772.png) . Equality holds if and only if
Var
. Equality holds if and only if
Var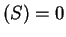 , i.e.
, i.e.  is constant with probability one. If we assume finite
fourth moments and
Var
is constant with probability one. If we assume finite
fourth moments and
Var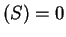 , then we also have
Var
, then we also have
Var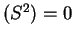 and
and
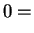 Var Var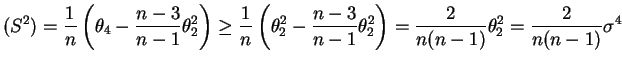 |
|
since
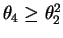 . So equality implies
. So equality implies  and
thus
and
thus
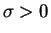 implies
implies
![$ E[S] < \sigma$](img780.png) .
.




Next: Assignment 13
Up: 22S:193 Statistical Inference I
Previous: Assignment 12
Luke Tierney
2004-12-03

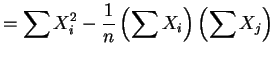

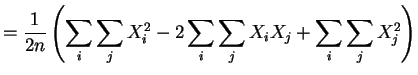
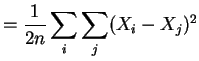
![$ E[X_{i}]=\theta_{1}=0$](img701.png) . Then
. Then
![$\displaystyle E[S^{2}] = \sigma^{2} = \theta_{2}$](img702.png)
![$\displaystyle E[S^{4}] = \frac{1}{4n^{2}(n-1)^{2}} \sum_{i}\sum_{j}\sum_{k}\sum_{\ell} E[(X_{i}-X_{j})^{2}(X_{k}-X_{\ell})^{2}]$](img703.png)
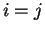 or
or 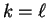 , then
, then
![$ E[(X_{i}-X_{j})^{2}(X_{k}-X_{\ell})^{2}]=0$](img706.png) . If all
. If all
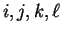 are different, then
are different, then
![$\displaystyle E[(X_{i}-X_{j})^{2}(X_{k}-X_{\ell})^{2}] = E[(X_{1}-X_{2})^{2}]^{2} = (2\sigma^{2})^{2} = 4 \theta_{2}^{2}$](img708.png)
 , say
, say 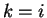 , then
, then
![$\displaystyle E[(X_{i}-X_{j})^{2}(X_{i}-X_{\ell})^{2}]$](img711.png)
![$\displaystyle = E[(X_{i}^{2}-2X_{i}X_{j}+X_{j}^{2}) (X_{i}^{2}-2X_{i}X_{\ell}+X_{\ell}^{2})]$](img712.png)
![$\displaystyle = E[ \begin{aligned}[t]& X_{i}^{4}-2X_{i}^{3}X_{j}+X_{i}^{2}X_{j}...
...i}^{2}X_{\ell}^{2}-2X_{i}X_{j}X_{\ell}^{2}+X_{j}^{2}X_{\ell}^{2}] \end{aligned}$](img713.png)
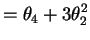
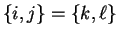 , then
, then
![$\displaystyle E[(X_{i}-X_{j})^{2}(X_{i}-X_{\ell})^{2}]$](img711.png)
![$\displaystyle = E[(X_{i}-X_{j})^{4}]$](img716.png)
![$\displaystyle = E[X_{i}^{4}-4X_{i}^{3}X_{j}+6X_{i}^{2}X_{j}^{2}-4X_{i}X_{j}^{3} + X_{j}^{4}]$](img717.png)
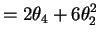
![$\displaystyle E[S^{4}]$](img719.png)
![$\displaystyle = \frac{1}{4n^{2}(n-1)^{2}} \begin{aligned}[t][&n(n-1)(n-2)(n-3) ...
..._{4}+3\theta_{2}^{2}) &+ 2n(n-1)(2 \theta_{4}+6\theta_{2}^{2})] \end{aligned}$](img720.png)
![$\displaystyle = \frac{1}{4n(n-1)}\left[ 4(n-2)(n-3)\theta_{2}^{2} + 4(n-2)(\theta_{4}+3\theta_{2}^{2}) + 4(\theta_{4}+3\theta_{2}^{2})\right]$](img721.png)
![$\displaystyle = \frac{1}{n(n-1)} [(n-1)\theta_{4}+((n-2)(n-3)+3(n-2)+3)\theta_{2}^{2}]$](img722.png)
![$\displaystyle = \frac{1}{n(n-1)} [(n-1)\theta_{4}+(n^{2}-2n+3)\theta_{2}^{2}]$](img723.png)
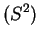
![$\displaystyle = E[S^{4}]-\frac{n(n-1)}{n(n-1)}\theta_{2}^{2}$](img725.png)
![$\displaystyle =\frac{1}{n(n-1)}[(n-1)\theta_{4}+(n^{2}-2n+3-n^{2}+n)\theta_{2}^{2}]$](img726.png)
![$\displaystyle =\frac{1}{n(n-1)}[(n-1)\theta_{4}-(n-3)\theta_{2}^{2}]$](img727.png)
![$\displaystyle =\frac{1}{n}\left[\theta_{4}-\frac{n-3}{n-1}\theta_{2}^{2}\right]$](img728.png)
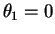 .
.
![$\displaystyle E[\overline{X}S^{2}]$](img730.png)
![$\displaystyle = \frac{1}{2n^{2}(n-1)} \sum_{i}\sum_{j}\sum_{k} E[(X_{i}-X_{j})^{2}X_{k}]$](img731.png)
![$\displaystyle = \frac{1}{2n^{2}(n-1)} 2n(n-1) E[(X_{1}-X_{2})^{2}X_{1}]$](img732.png)
![$\displaystyle = \frac{1}{n} E[X_{1}^{3}-2X_{1}^{2}X_{2}+X_{1}{X_{2}^{2}}]$](img733.png)
![$\displaystyle = \frac{1}{n} E[X_{1}^{3}] = \frac{1}{n}\theta_{3}$](img734.png)
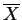 and
and  are uncorrelated if and only if
are uncorrelated if and only if
 .
.
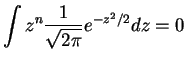
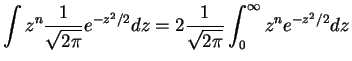
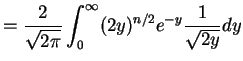
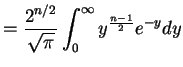
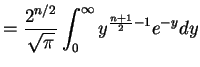
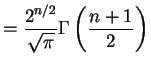
![$\displaystyle E[Z^{n}] = (n-1)\times(n-3)\times \cdots\times 3\times1 = \frac{n!}{\left(\frac{n}{2}\right)!2^{n/2}}$](img757.png)
![$\displaystyle E[(X-\mu)^{n}] = \begin{cases}0 & \text{$n$ odd} \frac{n!}{\left(\frac{n}{2}\right)!2^{n/2}}\sigma^{n} & \text{$n$ even} \end{cases}$](img758.png)

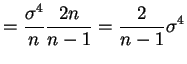
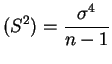 Var
Var