Then
So
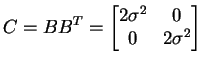 |
and
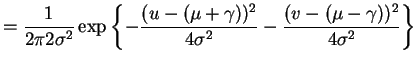 |
||
where
- a.
- The mean of
 is
is
![$\displaystyle E[Y] = E[E[Y\vert X]] = E[X] = 1/2$](img650.png)
The variance isVar 
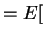 Var
Var![$\displaystyle (Y\vert X)] +$](img651.png) Var
Var![$\displaystyle (E[Y\vert X]) = E[X^2] +$](img652.png) Var
Var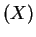
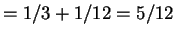
The covariance isCov 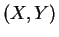
![$\displaystyle = E[(Y-\mu_Y)(X-\mu_X)] = E[E[Y-\mu_Y\vert X](X-\mu_X)]$](img655.png)
![$\displaystyle = E[(X - \mu_X)^2] =$](img656.png) Var
Var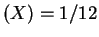
- b.
- The conditional distribution of
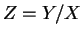 , given
, given 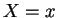 is
is 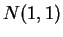 . Since this conditional distribution does not depend
on
. Since this conditional distribution does not depend
on 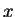 ,
, 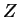 and
and 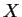 are independent.
are independent.
- a.
- Condition on
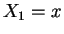 :
:
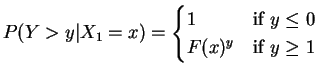
i.e.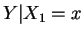 is geometric with
is geometric with
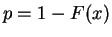 . So for
. So for 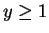
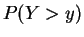
![$\displaystyle = E[F(X_{1})^{y}] = \int_{0}^{1}u^{y}du$](img669.png)
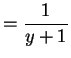
since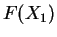 is uniform on
is uniform on ![$ [0,1]$](img672.png) by the probability integral
transform. So for
by the probability integral
transform. So for


Alternative argument: For
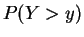
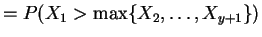
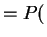 argmax
argmax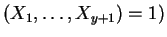
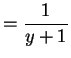
by symmetry. - b.
- Using
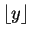 to denote the largest integer
less than or equal to
to denote the largest integer
less than or equal to  we have
we have
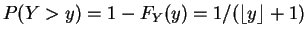 for all
for all 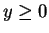 . So
. So
![$\displaystyle E[Y]$](img309.png)
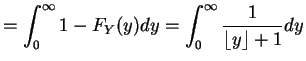
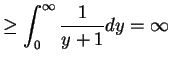
- a.
- Suppose
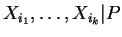 are independent
Bernoulli(
are independent
Bernoulli(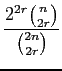 ). Then
). Then
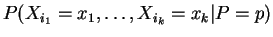
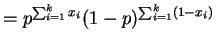
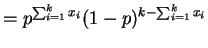
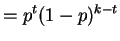
So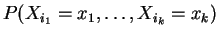
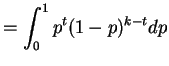
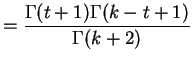

- b.
-
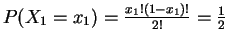 . So
. So
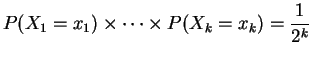
For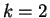 ,
,
(0,0) (0,1) (1,0) (1,1) 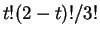
1/3 1/6 1/6 1/3 independent 1/4 1/4 1/4 1/4
