so
and thus
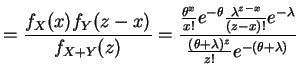 |
||
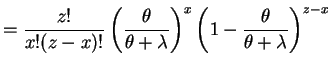 |
for
- a.
- For
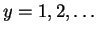 ,
,
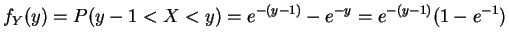
So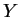 is geometric(
is geometric(
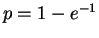 ).
).
- b.
-
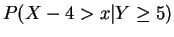
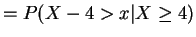
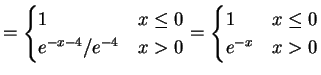
This is an exponential distrbution.For any
 ,
,
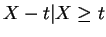 is Exponential(1).
is Exponential(1).
- a., b.
- Suppose the
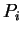 are independent random variables
with values in the unit interval and common mean
are independent random variables
with values in the unit interval and common mean 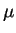 . Since the
. Since the
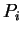 are independent and each
are independent and each 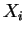 only depends on
only depends on 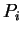 , the
, the
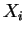 are marginally independent as well. Each
are marginally independent as well. Each 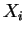 takes on
only the values 0 and 1, so the marginal distributions of the
takes on
only the values 0 and 1, so the marginal distributions of the
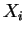 are Bernoulli with success probability
are Bernoulli with success probability
![$\displaystyle P(X_i = 1) = E[P(X_i=1\vert P_i)] = E[P_i] = \mu$](img538.png)
So the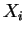 are independent Bernoulli(
are independent Bernoulli(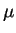 ) random variables and
therefore
) random variables and
therefore
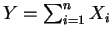 is Binomial(
is Binomial(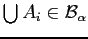 ,
, 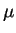 ). If the
). If the
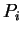 have a Beta(
have a Beta(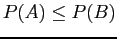 ,
,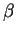 ) distribution then
) distribution then
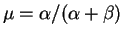 and therefore
and therefore
![$\displaystyle E[Y]$](img309.png)

Var 
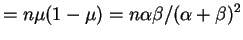
- c.
- For each
![$\displaystyle E[X_i]$](img544.png)
![$\displaystyle = E[E[X_i\vert P_i]] = E[n_iP_i] = n_iE[P_i] = n_i \frac{\alpha}{\alpha+\beta}$](img545.png)
Var 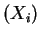
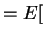 Var
Var![$\displaystyle (X_i\vert P_i)] +$](img548.png) Var
Var![$\displaystyle (E[X_i\vert P_i])$](img549.png)
![$\displaystyle = E[n_i P_i(1-P_i)] +$](img550.png) Var
Var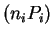
![$\displaystyle = n_i E[P_i(1-P_i)] + n_i^{2}$](img552.png) Var
Var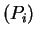
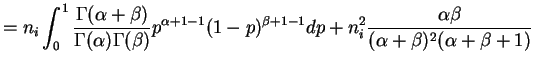
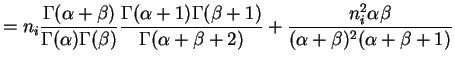
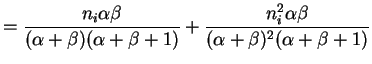
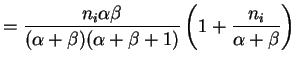
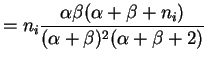
Again the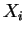 are marginally independent, so
are marginally independent, so
![$\displaystyle E[Y]$](img309.png)
![$\displaystyle = \sum E[X_i] = \frac{\alpha}{\alpha+\beta}\sum_{i=1}^k n_i$](img559.png)
Var 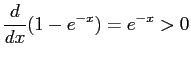
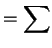 Var
Var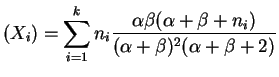
The marginal distribution of
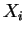 is called a beta-binomial
distribution. The density of
is called a beta-binomial
distribution. The density of 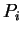 is
is
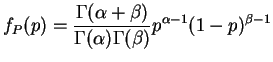
for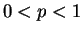 . So the PMF of
. So the PMF of 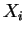 is
is
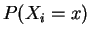
![$\displaystyle = E[P(X_i = x\vert P_i)] = E\left[\binom{n_i}{x}P_i^x(1-P_i)^{n_i-x}\right]$](img565.png)
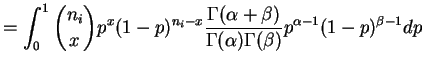
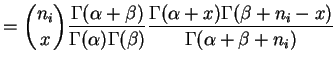
The joint density of
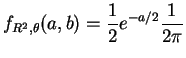 |
for
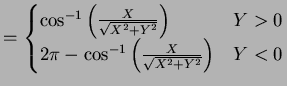 |
This is messy to differentiate; instead, compute
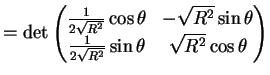 |
||
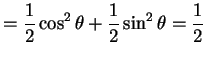 |
So
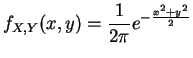 |
Thus
- a.
-

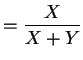
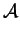
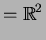

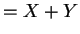
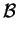
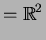
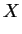
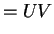
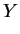
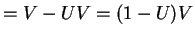
So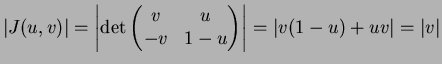
Thus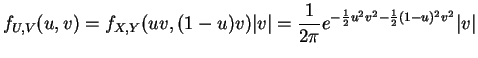
and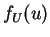
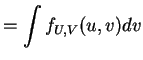
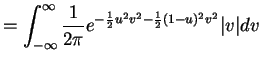
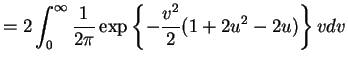
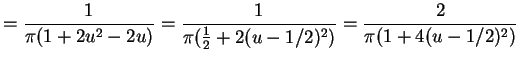
This is a Cauchy(1/2,1/2) density. - b.
-

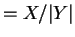

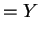
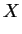
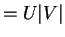
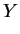
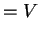
with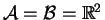 . So
. So
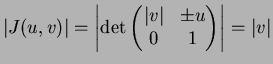
and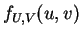
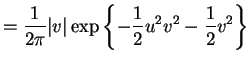
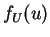
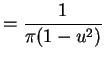
- a.
-
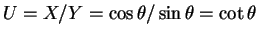 .
.
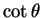 is one to one on
is one to one on 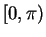 , and periodic with period
, and periodic with period
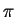 . So
. So
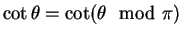 . Since
. Since
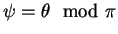 is uniformly distributed on
is uniformly distributed on 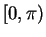 and
and 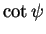 is one to one on
is one to one on 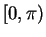 we have
we have
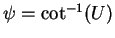 and
the density of
and
the density of 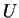 is
is
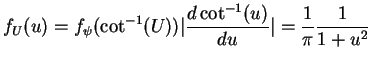
which is a standard Cauchy density. - b.
-
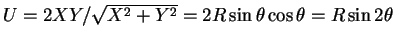 . Since
. Since
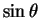 and
and
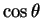 are periodic
with period
are periodic
with period 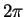 and since
and since
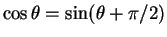 we have
we have
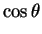
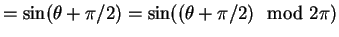
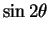
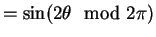
Since both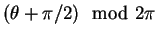 and
and
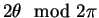 are
uniformly distributed on
are
uniformly distributed on 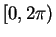 this shows that
this shows that
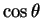 ,
,
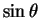 and
and
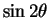 all have the same
marginal distribution, and therefore
all have the same
marginal distribution, and therefore
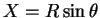 has the same
distribution as
has the same
distribution as
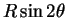 .
.
