- a.
- Toss coin 4 times:
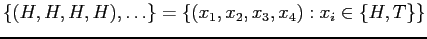
or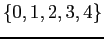
- b.
- Count number of insect-damaged leaves:
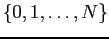
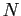 = # leaves (or upper bound)
= # leaves (or upper bound)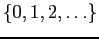
if no upper bound is available
- c.
- Measure lifetime in hours:
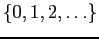
if rounded (can put in upper limit) 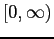
if fractional hours are allowed
- d.
- Weight of ten-day-old rats:
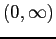
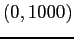
in grams
- e.
- Proportion of defectives:
![$\displaystyle [0,1]$](img12.png)
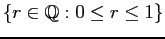
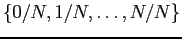
if shipment size 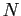 is known
is known
- a.
-
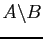 is defined as
is defined as
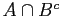 . To
see that
. To
see that
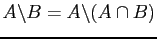 :
:

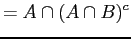
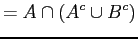
De Morgan's law 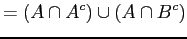
distributive law 
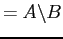
- b.
-
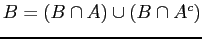 :
:
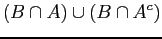
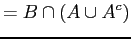
distributive law 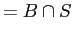
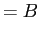
- c.
- By definition.
- d.
-
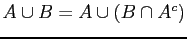 :
:
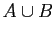
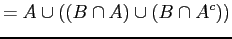
by part (b) 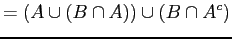
associative law 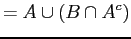
- a.
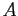 or
or 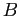 or both:
or both:
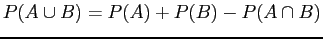
- b.
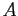 or
or 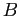 but not both:
but not both:
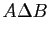
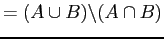
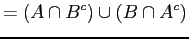
and the sets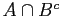 and
and
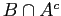 are disjoint. Since
are disjoint. Since
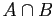 and
and
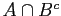 are disjoint and their union is
are disjoint and their union is 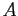 ,
,
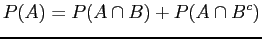
and therefore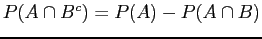 . Similarly
. Similarly
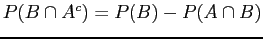 and therefore
and therefore
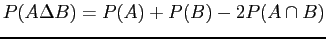
- c.
- At least one of
 or
or  :
: 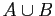 .
.
- d.
- At most one of
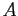 or
or 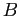 = not
= not 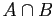 =
=
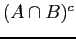 :
:
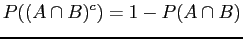
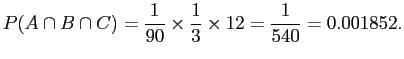 |
but
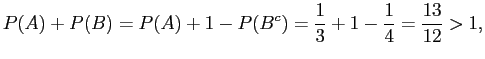 |
so
