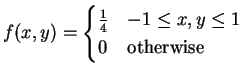 |
- a.
-
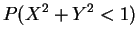
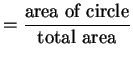
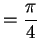
- b.
-
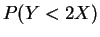
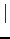 by symmetry, or
by symmetry, or
![$\displaystyle =\left[\frac{y}{4}-\frac{y^{2}}{16}\right]_{-1}^{1} = \frac{1}{4}+\frac{1}{4}=\frac{1}{2}$](img459.png)
- c.
-
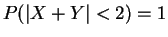
- a.
-
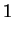
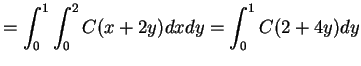
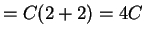
So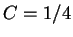 .
.
- b.
-
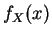
![$\displaystyle = \int_{0}^{1}\frac{1}{4}(x+2y)dy 1_{[0,2]}(x)$](img466.png)
![$\displaystyle = \frac{1}{4}(x+1) 1_{[0,2]}(x)$](img467.png)
- c.
-
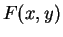
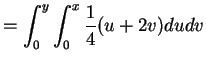
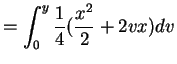
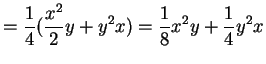
for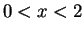 and
and 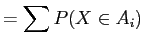 .
.
- d.
-
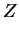
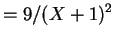
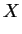
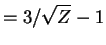
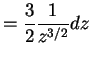
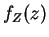
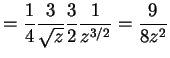
for![$ z \in [1,9]$](img480.png) .
.
- a.
-
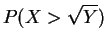
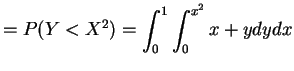
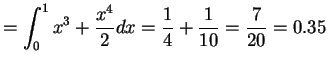
- b.
-
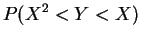
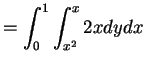
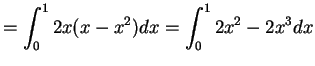
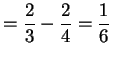
- a.
-
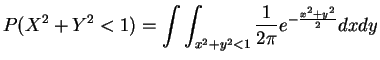
Can do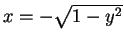 to
to
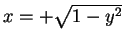 , or
, or
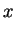
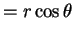
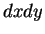
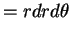
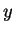
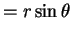
for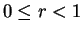 and
and
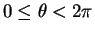 :
:
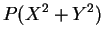
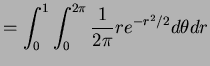
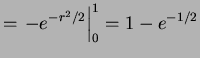
- b.
- The density of
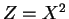 is
is
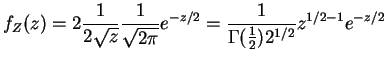
for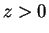 ; this is a
Gamma
; this is a
Gamma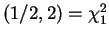 density.
Using a computer,
density.
Using a computer,
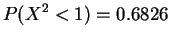
![\includegraphics[height=1.25in]{4-7.eps}](img507.png)
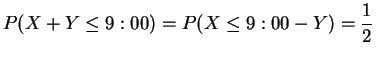 |
(Is independence a reasonable assumption?)
