- a.
-
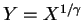 ,
,  Exponential(
Exponential(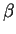 ).
).
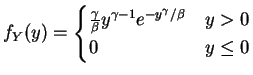
![$\displaystyle E[Y^{k}]$](img335.png)
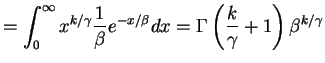
![$\displaystyle E[Y]$](img309.png)
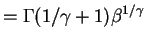
Var 
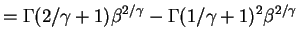
- b.
-
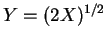 ,
,
 Gamma
Gamma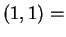 Exponential
Exponential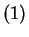 .
.
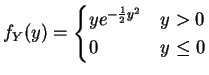
![$\displaystyle E[Y]$](img309.png)
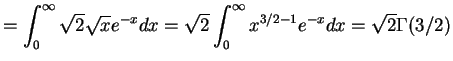
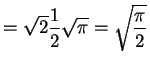
![$\displaystyle E[Y^{2}]$](img234.png)
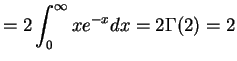
Var 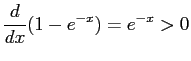

- c.
-
 Gamma
Gamma ,
,  .
.
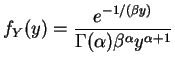
for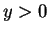 . Moments:
. Moments:
![$\displaystyle E[Y^k] = E[X^{-k}] = \int_0^\infty \frac{x^{\alpha-k-1} e^{-\beta x}}{\Gamma(\alpha) \beta^\alpha} = \frac{\Gamma(\alpha-k)}{\Gamma(\alpha)\beta^k}$](img351.png)
for and
and
![$ E[Y^{-k}] = \infty$](img353.png) for
for
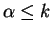 . So
for
. So
for
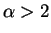
![$\displaystyle E[Y]$](img309.png)
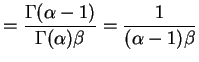
![$\displaystyle E[Y^2]$](img357.png)

Var 

- d.
-
 Gamma
Gamma ,
,
 .
.

![$\displaystyle E[Y^{k}]$](img335.png)
![$\displaystyle = E[X^{k/2}] = \int_{0}^{\infty}\frac{1}{\Gamma(3/2)}x^{k/2+3/2-1}e^{-x}dx$](img363.png)
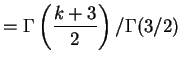
![$\displaystyle E[Y]$](img309.png)

![$\displaystyle E[Y^{2}]$](img234.png)
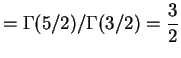
Var 
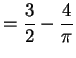
- e.
-
 Exponential
Exponential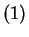 ,
,
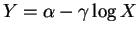

![$\displaystyle E[Y]$](img309.png)
![$\displaystyle = \alpha-\gamma E[\log X]$](img370.png)
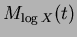
![$\displaystyle = E[e^{t \log X}] = E[X^{t}] = \int_{0}^{\infty}x^{(t+1)-1}e^{-x}dx = \begin{cases}\Gamma(t+1) & t > -1 \infty & t \le -1 \end{cases}$](img372.png)
![$\displaystyle E[\log X]$](img373.png)
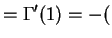 Euler's number
Euler's number
![$\displaystyle E[(\log X)^{2}]$](img376.png)
 Euler's number
Euler's number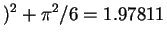
Var 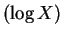
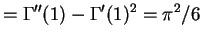
Once the moment generating function has been obtained, the rest can be done in Mathematica: The derivative of the Gamma function is obtained asIn[23]:= D[Gamma[x],x] Out[23]= Gamma[x] PolyGamma[0, x]
The value at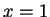 is obtained using the ``slash-dot'' operator:
is obtained using the ``slash-dot'' operator:
In[24]:= % /. x->1 Out[24]= -EulerGamma
The variable%refers to the last output expression. The numerical value is obtained to 10 digits byIn[25]:= N[%,10] Out[25]= -0.5772156649
The second derivative of the Gamma function is
In[26]:= D[Out[23],x] 2 Out[26]= Gamma[x] PolyGamma[0, x] + Gamma[x] PolyGamma[1, x]Substituting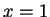 produces
produces
In[27]:= % /. x->1 2 2 Pi Out[27]= EulerGamma + --- 6 In[28]:= N[%,10] Out[28]= 1.978111991
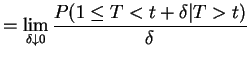 |
||
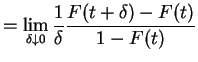 |
||
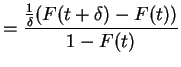 |
||
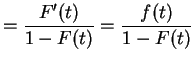 |
and
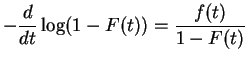 |
The quantity
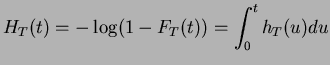 |
is called the cumulative hazard function, and
Constant hazard:
an exponential distribution.
Power hazard: Weibull.
- a.
-
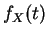
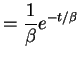
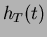

- b.
-
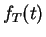
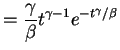
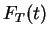
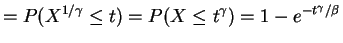
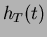
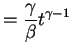
- c.
-
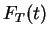
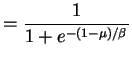
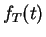
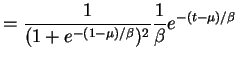
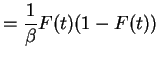
So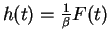 .
.
- a.
-
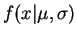
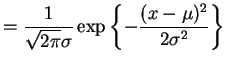
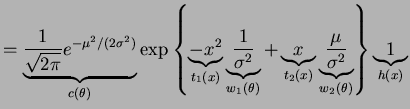
- b.
-
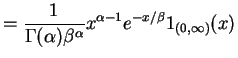
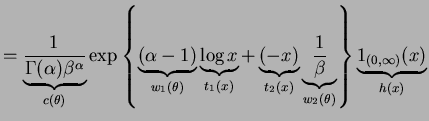
- c.
-
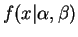
![$\displaystyle = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1} 1_{[0,1]}(x)$](img410.png)
![$\displaystyle = \underbrace{ \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\...
...a)} \underbrace{\log (1-x)}_{t_{2}(x)}\right\} \underbrace{1_{[0,1]}(x)}_{h(x)}$](img411.png)
- d.
-
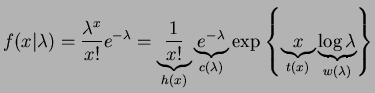
- e.
-
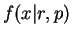
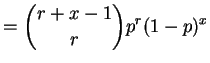
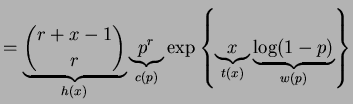
- a.
- For the binomial,
 ,
,
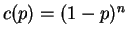 ,
and
,
and 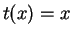 . The variance
Var
. The variance
Var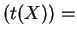 Var
Var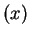 satisfies
satisfies
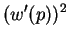 Var
Var![$\displaystyle (X) = -\frac{d^2}{dp^2}c(p) - w''(p)E[X]$](img422.png)
Now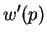
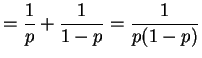

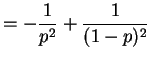
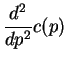
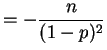
So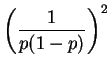 Var
Var
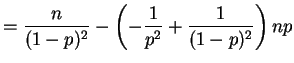
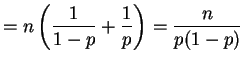
and thus Var
- b.
- For the Beta distribution
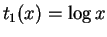 and
and
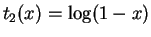 . The function
. The function  cannot be expressed as
a linear combination of
cannot be expressed as
a linear combination of 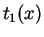 and
and 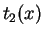 , so the identities in
Theorem 3.4.2 cannot be used to find the mean and variance of
, so the identities in
Theorem 3.4.2 cannot be used to find the mean and variance of 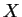 .
.
If
 Poisson
Poisson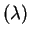 then
then 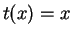 ,
,
 , and
, and
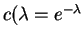 . So
. So
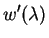
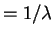
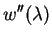
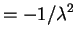
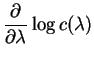
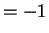
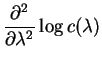
So Theorem 3.4.2 produces the equations![$\displaystyle E[X/\lambda]$](img448.png)
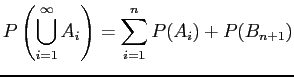
Var 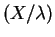
![$\displaystyle = E[X/\lambda^2]$](img450.png)
with solutions![$ E[X] = \lambda$](img451.png) and
Var
and
Var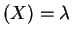 .
.
