



Next: Assignment 7
Up: 22S:193 Statistical Inference I
Previous: Assignment 6
- 2.27
- a.
-
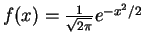 has a unique mode
at
has a unique mode
at 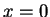 .
.
- b.
- For
any
![$ x \in [0,1]$](img293.png) is a mode.
is a mode.
- c.
- Suppose, without loss of generality, that the point of
symmetry is the origin. Suppose, without loss of generality, that
the density is unimodal with mode
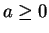 . For
. For
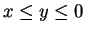 we have
we have
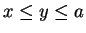 and therefore by unimodality
and therefore by unimodality
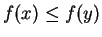 and
and
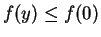 . For
. For
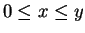 we have
we have
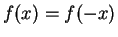 and
and
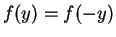 by symmetry, and
by symmetry, and
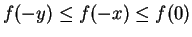 by unimodality as before. So the point of symmetry 0
is a mode.
by unimodality as before. So the point of symmetry 0
is a mode.
- d.
- The exponential distribution
is unimodal with mode 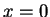 since
since  is non-decreasing on
is non-decreasing on
![$ (-\infty,0]$](img305.png) and non-increasing (in fact strictly decreasing) on
and non-increasing (in fact strictly decreasing) on
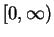 . If you switch the equality sign to the other side,
it is not unimodal.
. If you switch the equality sign to the other side,
it is not unimodal.
- 2.30
- LATEX2Html is giving me grief about this one-it is available in
the pdf version.
- 2.33
- LATEX2Html is giving me grief about this one-it is available in
the pdf version.
- 2.38
- LATEX2Html is giving me grief about this one-it is available in
the pdf version.




Next: Assignment 7
Up: 22S:193 Statistical Inference I
Previous: Assignment 6
Luke Tierney
2004-12-03
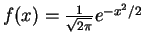 has a unique mode
at
has a unique mode
at 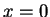 .
.
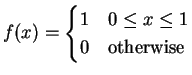
![$ x \in [0,1]$](img293.png) is a mode.
is a mode.
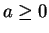 . For
. For
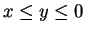 we have
we have
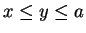 and therefore by unimodality
and therefore by unimodality
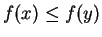 and
and
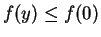 . For
. For
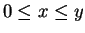 we have
we have
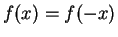 and
and
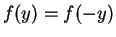 by symmetry, and
by symmetry, and
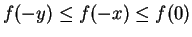 by unimodality as before. So the point of symmetry 0
is a mode.
by unimodality as before. So the point of symmetry 0
is a mode.
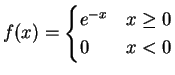
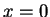 since
since  is non-decreasing on
is non-decreasing on
![$ (-\infty,0]$](img305.png) and non-increasing (in fact strictly decreasing) on
and non-increasing (in fact strictly decreasing) on
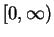 . If you switch the equality sign to the other side,
it is not unimodal.
. If you switch the equality sign to the other side,
it is not unimodal.
