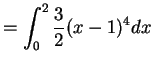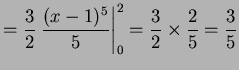 |
So
 |
||
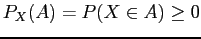 |
||
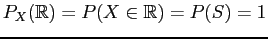 |
||
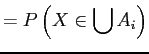 |
and
 |
So for
 |
||
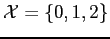 |
||
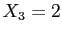 |
For the alternative approach,
Since
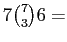 |
and thus
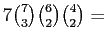 |
- a.
-
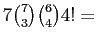
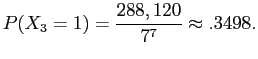
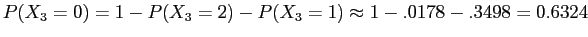

- b.
-
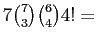
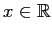
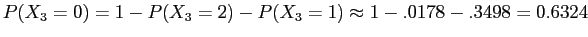

- c.
-
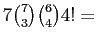
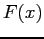
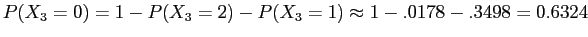
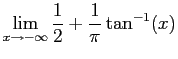
- a.
-
![$\displaystyle E[X^{2}]$](img220.png)
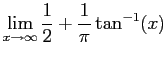
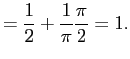
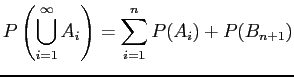
or![$\displaystyle E[X^{2}] = E[Y]$](img224.png)
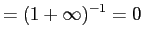
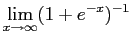
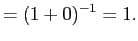
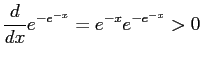
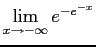
- b.
-
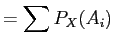
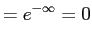
![$\displaystyle E[Y] = E[\vert X\vert]$](img231.png)
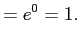
![$\displaystyle = 2 \left[\left.-\frac{1}{\sqrt{2\pi}}e^{-y^{2}/2}\right\vert _{0}^{\infty} \right] = 2\frac{1}{\sqrt{2\pi}} = \sqrt{\frac{2}{\pi}}$](img233.png)
![$\displaystyle E[Y^{2}]$](img234.png)
![$\displaystyle = E[X^{2}] = 1$](img235.png)
Var 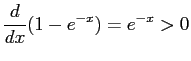
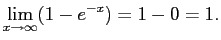
- (a)
-
![$\displaystyle E[X]$](img238.png)
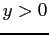


[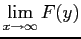 if
if
![$ E[X]<\infty$](img243.png) ]
]
- (b)
- Write the expectation as
![$\displaystyle E[X] = \sum_{i=0}^\infty i f_X(i) = \sum_{i=1}^\infty i f_X(i) = \sum_{i=1}^\infty \sum_{j=1}^i f_X(i)$](img244.png)
replacing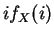 by a sum that adds up
by a sum that adds up 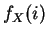
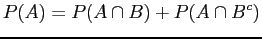 times.
Change the order of summation:
times.
Change the order of summation:

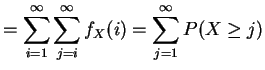
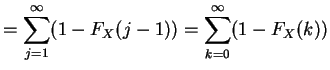
Since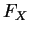 is a right-continuous step function with jumps at the
integers,
is a right-continuous step function with jumps at the
integers,
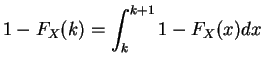
for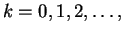 so
so
![$\displaystyle E[X] = \int_0^\infty 1 - F_X(x) dx$](img253.png)
in this case as well
The result holds for all non-negative random variables. A general derivation:
![$\displaystyle = E\left[\int_{0}^{X}1du\right]$](img254.png) |
||
![$\displaystyle = E\left[\int_{0}^{\infty}h(X,u)du\right]$](img255.png) |
where
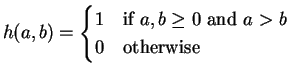 |
Reverse order of integration:
![$\displaystyle E[X] = \int_{0}^{\infty}E[h(X,u)]du$](img257.png) |
For fixed
So
![$\displaystyle E[X] = \int_{0}^{\infty} 1-F(u) du$](img262.png) |
for any
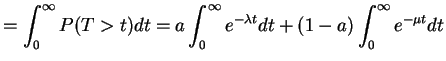 |
||
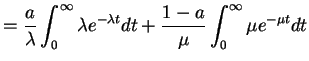 |
||
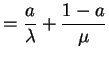 |
- a.
-
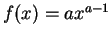 ,
,  ,
, 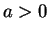 .
.
![$\displaystyle E[X]$](img238.png)
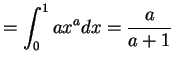
![$\displaystyle E[X^{2}]$](img220.png)
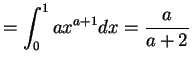
Var 
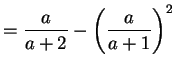
- b.
-
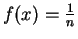 ,
,
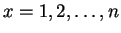 .
.
![$\displaystyle E[X]$](img238.png)
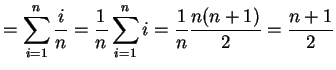
![$\displaystyle E[X^{2}]$](img220.png)

Var 

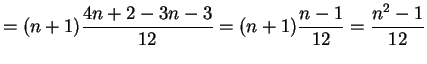
- c.
-
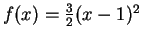 ,
, 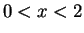 .
.
![$\displaystyle E[X]$](img238.png)

Var 
![$\displaystyle = E[(X-1)^{2}]$](img287.png)