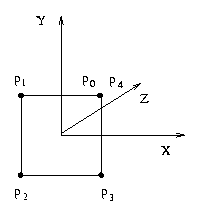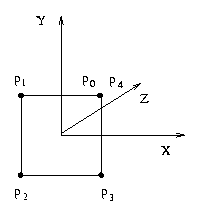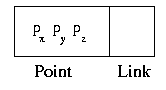22C:030/115 Programming Techniques and Data Structures

Program 3: Polylines and Bags of Polylines

DUE DATES:

• Class implementation and test program (items 2-7 below) 10/20/99 (NOTE CHANGE!)
• Demonstration program and data set (items 7-8) 10/27/99 (NOTE CHANGE!)

This program requires you to design, implement and test two classes: Polyline and Bag of Polylines. The Polyline class represents a connected sequence of three-dimensional line segments. The Bag of Polylines will be used to store a collection of Polylines that define a scene consisting of line drawn objects. You are to write a program demonstrating your classes that generates a set of polylines approximating several mathematically defined shapes including spiral curves, sine waves, and Kock snowflakes. The assignment will give you experience in developing a clear specification from a problem statement, experience in the use of linked lists, and additional experience in software coding and testing.

What to submit:

You should submit a directory that includes:

1. README: A file giving a overview of the contents of the directory including:
• Your name and section number.
• A short (2-3 sentence description) of the assignment.
• A one sentence description of each file in the directory.
• An explanation of how to compile your programs.
2. polyline.h: The header file for the new Polyline class.
3. polyline.template: The implementation file for the new Polyline class.
4. bag.h: The header file for the bag of Polylines class.
5. bag.template: The implementation file for the bag of Polylines class.
6. polylinetest.cxx: An program that tests the Polyline class.
7. polylinedemo.cxx: An demonstration program.
8. polyline.dat: The output of your demonstration program including polylines approximating spirals, sine curves, a Koch snowflake.
9. A printed copy of the files README, polyline.h, polyline.template, bag.h, bag.template, polylinetest.cxx, and, polylinedemo.cxx to be submitted in lecture on the due date.

The Polyline Class

p = ((1.0,1.0,0.0), (-1.0,1.0,0.0), (-1.0,-1.0,0.0),

                                (1.0,-1.0,0.0), (1.0,1.0,0.0)

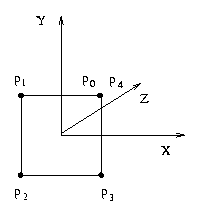
In addition to its shape, a Polyline should have a color attribute expressed by three values giving red, green, and blue components of the color. You should use the Point3D class from the first project to represent the points in a line segment.

A Polyline must be represented as a linked list of points.  You may choose to use either a singly or doubly linked list. The node structure for a singly linked list is pictured below.
 

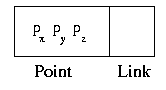
Your class should include the following functions and operations:

• A default constructor.
• A copy constructor.
• A destructor.
• A set of member functions to add and remove points from a Polyline.  You should include the operations specified in the List class defined on pages 120-121 of the text book.
  
  
• An assignment operator:

p1 = p2;

• An addition operator that returns that the concatenation of two Polylines (i.e. the combined series of points.)

p3 = p1 + p2;

• Member functions to rotate a Polyline about the X, Y, and Z axes. To rotate a Polyline, each point of the Polyline must be rotated in the same way:

p.rotateX(angle);

p.rotateY(angle);

p.rotateZ(angle);

• A member function that shifts a Polyline. To shift a Polyline, each point of the Polyline must be shifted in the same way:

p.shift(shiftx, shifty, shiftz);

where shiftx, shiftx, and shiftx are doubles giving the amount to shift in the x, y, and z directions.


• Member functions to get and set the color of a Polyline.

p.colorset(red, green, blue);

rvalue = p.colorgetRed();

gvalue = p.colorgetGreen();

bvalue = p.colorgetBlue();

where red, green, and blue are the components of the color. The values of red, green, and blue must be in the range 0.0-1.0.


• An output operator << that prints a polyline. Polylines should be printed in OpenInventor format, a graphics toolkit developed by Silicon Graphics Inc. An example of a polyline in OpenInventor format is shown below:

Material {
        diffuseColor    0.8 0.8 0.0
}

Coordinate3 {
    point       [     0 1.2142 0.7453,
                      0 1.2142 -0.7453,
                     -1.2142 0.7453 0,
                     -0.7453 0 1.2142,
                      0.7453 0 1.2142,
                      1.2142 0.7453 0
                 ]
}
LineSet {
}

The format includes three definitions, Material, Coordinate3, and LineSet. You must include all three for each polyline. The Material definition specifies the color with which to render subsequent objects. The three color values are the red, green, and blue components. The Coordinate3 definition gives a list of three dimensional points. You should print all of the points in the polyline here. The LineSet defintion indicates that the preceeding points should be interpreted as a line set. For an example of an output file containing two polylines see the file LineSet in the class programs directory (/group/class/22c030/programs). To convert this file to OpenInventor format you must add the header line:

     #Inventor V2.0 ascii

as the first line in the file. The file LineSet.iv has been modified in this way. You can now view the OpenInventor file with the command:

     %ivview LineSet.iv

Alternatively, you can simply use the program plineview to display file produced by your program. For example, try

     %plineview LineSet

The Bag Class

You are to design, implement, and test a bag class that stores a collection of Polylines. You should use the bag5 class defined in the text book and provided for you in the class software repository (see the chapt14 directory). The templated list and linked list toolkit stored in the chapt14 directory should also be helpful to get you started. Because the comparison operator is complex for Polylines, we will only add Polylines to the bag. Therefore, you should NOT include member functions for remove and occurrences. You should add member functions to rotate, translate, and set the color of all Polylines in a bag and an operator to print a bag. The print operator should call the print method for all Polylines in the bag.

A Test Program

You are to write a program that tests your implementation of the Polyline and Bag class. This program should carefully test all Polyline and Bag member functions. It is your responsibility to demonstrate that each member function satisfies your specifications. Your grade will be determined, in part, by the quality of your testing.

A Demonstration Program

You are to write a second program that demonstrates the use of polylines. This program should include at least one example of a Polyline approximating a spiral and a sine curve. It should also include a Koch snowflake.
• (Specifications for the polyline generating functions are given here.)

Bonus Credit

There will be a contest for the most artistic data set. The top five data sets, judged on their artistic merits by the class, will get 10 bonus points on the project. Artwork should be separately submitted to the art submission directory. Each student can submit one or two art files by 10/29/99. A gallery of submissions from last year's class are stored in the directory /group/class/22c030/gallery.