Core Memory The dominant technology from 1960 to 1980 by Douglas W. Jones THE UNIVERSITY OF IOWA Department of Computer Science

Contents

• Introduction

• Early Core
  A memory module found in the U of Iowa Physics Department's Van de Graff accelerator lab shortly before demolition. When found, it was in what appears to have been its factory original packaging, suggesting that it was a never-used spare part.

  Date:   1960?
  Capacity: 4K × 2
  Core area per bit: 6.45 mm²
  Core diameter: 1.96 mm

• A DEC Type 184A memory module
  A memory module from a PDP-8 computer. This minicomputer was the 1st generation of the PDP-8 line. These machines were mostly built from discrete transistors, although small numbers of hybrid integrated circuits were used. The power supply voltages were +10V and -15V, and logic levels of -3V and 0V.

  Date:   1965
  Capacity: 4096 × 12
  Core area per bit: 1 mm²
  Core diameter: 0.89 mm

• A PDP-8/L module
  A memory module from a PDP-8/L computer. This minicomputer was the 3rd generation of the PDP-8 line, although the PDP-8/I, the second generation machine, used the same module. These machines were early users of TTL integrated circuits.

  Date:   1970 (introduced 1968)
  Capacity: 4096 × 12
  Core area per bit: 0.64 mm²
  Core diameter: 0.76 mm

• HP 9100B module
  A memory module from an HP 9100B calculator. This was the expanded version of the first generation of HP's revolutionary line of programmable RPN calculators. It is noteworthy that this desktop machine did not use integrated circuits.

  Date:   1970 (introduced 1969, some say 1968)
  Capacity: 640 × 6
  Core area per bit: 0.89 mm²
  Core diameter: ?

• DEC MM8E module
  A memory module from a PDP-8/E found on a junk pile. When found, it was broken, but it has since been repaired. This minicomputer was the 4th generation of the PDP-8 line, and made extensive use of TTL integrated circuits.

  Date:   1972 (introduced 1970)
  Capacity: 4K × 12
  Core area per bit: 0.28 mm²
  Core diameter: 0.51 mm

• DEC MM8EJ module
  A memory module from a PDP-8/E purchased by the University of Iowa Psychology Department. It worked when obtained.

  Date:   1977 (introduced 1974)
  Capacity: 8K × 12
  Core area per bit: 0.13 mm²
  Core diameter: 0.46 mm

Introduction

Transformers: To understand how core memory works, it helps to understand a bit about how transformers work. The picture at the right shows an idealized transformer with 2 wires, D, the data-in wire, and S, the sense wire. The wires pass through a transformer core, shown here as a ring. What matters to the system is that each wire passes through the core. They are shown perpendicular to each other, and they are shown passing throug it just once. They need not be perpendicular, and in a power thransformer, they are usually wound around the core many times. None of this matters here. The core is shown as a ring, but it could just as easily be rectangular.

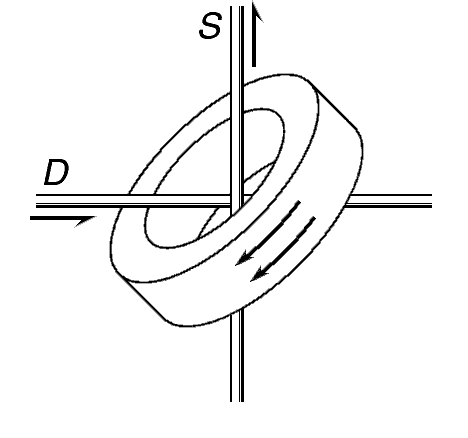
For the transformer to function, it must be made of a magnetic material. In a power transformer, we use soft magnetic materials, where the magnetization of the core is linearly proportional to the current through the core. If we push current through the data-in wire, it will magnetize the core, and the change in magnetization in the core will induce a voltage in the sense wire. The arrows show the direction of the current in the data-in wire, the direction in which the core is magnetized, and the direction that the voltage in the sense wire is attempting to push curent. If the sense wire is made into a loop with zero resistance, the current in the sense wire will be equal to the current in the data-in wire in such a way that the total magnetization of the core is always zero.

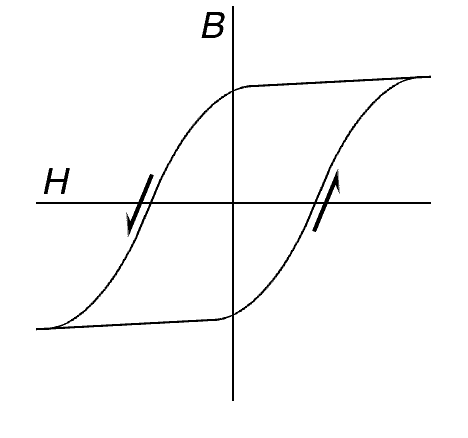
Hysteresis and Saturation: Real magnetic materials aren't like the ideal soft magnetic materials described above. First, they can only be magnetized up to some point. Above that point, we say that the core is saturated. Increasing the current above the saturation point doesn't increase the magnetization. Second, real ferromagnetic materials exhibit hysteresis. That is, once you apply some current to magnetize them, they tend to stay magnetized and you have to apply at least a little current in the opposite direction to get them completely demagnetized.

The B–H curve shown to the left illustrates both saturation and hysteresis. The horizontal axis (conventionally labeled H) shows the current through the core, while the vertical axis (conventionally labeled B) shows the magnetic field induced in the core by that current. As the current H increases, the rate at which the magnetic field B increases falls off. At the point where increasing H causes no appreciable increase in B, we say the core is saturated.

For hard magnetic materials, including the ferrite used in core memories, tool steel and the alloys used in permanent magnets, reducing the current H to zero leaves the core magnetized, so B is not zero. If the current is reversed to saturate the core in the opposite direction and then released, B will still be be non-zero, but now the core will be magnetized in the opposite direction.

Now, consider how a core made of a hard magnetic materal responds to a current pulse. If the core is already magnetized in the direction that current pulse would induce, the current pulse will only cause a small change in the magnetization, so only a small pulse will be seen on the sense line. In contrast, if the core is magnetized in the opposite direction, there will be a big change in the magnetization, so there will be a big pulse on the sense line.

Note: For the core memories discussed here, reading the data stored in a core always involves erasing that data. You have to set it to zero to see if it was a one. If you want the data to remain unchanged after reading, the control system must refresh the data by rewriting the bits that should be one.

Coincident Current Addressing: If we had just one data line per core, it would be difficult to build a large array of cores to store data without having separate read-write electronics for each core. In a coincident-current core memory, the data line D is split into two separate wires, X and Y, where the sum of the current in the two wires is sufficient flip the core's magnetic field, but the current in just one wire is not. This allows any single core in a rectangualr array of cores to be selected by applying simultaneous pulses to the X and Y wires that pass through that core. This idea, invented by Jay Forrester at MIT, is called coincident current memory addressing (see U.S. Patent 2,736,880, granted Feb. 28, 1956).

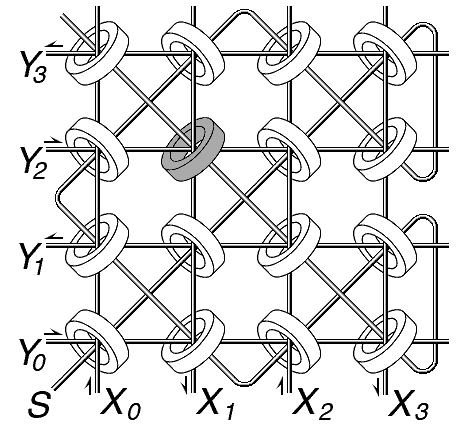
In the figure to the right, showing a plane of 16 cores, 4 per row. This requires 4 X select lines and 4 Y select lines. The arrows show the direction of current flow in each line when that line is used to write a one into the selected core. Applying simultaneous current pulses in this direction to the X₁ and Y₂ lines writes a one to just one core, shown shaded. Reversing the direction of the current pulses will write a zero to that core. There will be a pulse on the sense line of the magnetization of that core flips, and no pulse (or a much smaller pulse) if it does not.

If we are only interested in accessing one bit at a time, a read or write cycle would begin with negative pulses on both the selected X and Y lines in order to reset the addressed core to zero and read its previous value, and then a positive pulse on one select line (say the X line) with a positive pulse on the other select line (say the Y line) only when it is desired to write or restore that core to hold a one.

Core Stacks: If we want to organize the core memory as an array of words, where all the bits in a word can be simultaneously read or written, it is quite practical to stack core planes, as shown to the right. Here, we have shown a 16-word memory with just 2 bits per word. This is why the core memory subsystem of many early computers was referred to as a core stack. Note that it is the wiring of the X and Y lines that matters, not the physical stacking of the planes. Many later core memories were made with the core planes for each bit of the word set side-by-side.

In wiring a core stack, the corresponding X and Y lines of each plane are wired in series, while a separate sense line is used for each plane. For example, the X₁ line is threaded through the corresponding cores in both planes. Now, if we apply simultaneous pulses to the, X₁ and Y₂ lines, we will select two cores, one in each plane, shown shaded in the figure to the right. We can reset the sense of both cores with such a pulse, reading out their previous values on the two sense lines, S₀ and S₁.

The diagonal wiring of the sense line in the core plane was particularly troublesome. The meandering path through all of the cores minimizes the crosstalk between the X and Y lines and the sense line, but it prevents the cores from being tightly packed. The first wire through each row of cores, typically the X wire, could be pushed through a tightly packed stack of cores by machine, and semi-automated threading of the second wire, typically the Y wire, was pursued, but beyond that, this core layout effectively resisted automation.

Inhibit Logic: Unfortunately, we cannot selectively write data into the word with the logic described above. The first solution to the problem of selectively writing the bits in a core stack was to add a 4^th wire through each core known as the inhibit wire or I, as shown in the figure to the right.

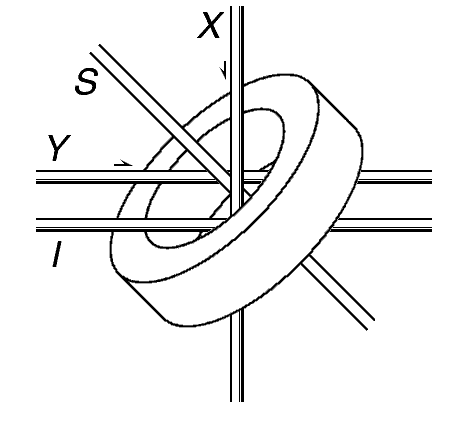
The inhibit wire is strung through all the wires of each core plane, parallel to one of the select lines. Here, it is shown parallel to the Y select line. When no current flows through the inhibit line, the Y select line operates normally. When it is desired to inhibit the writing of a one to this core plane, a pulse is sent on the inhibit line that is opposite to the direction of the pulse in the Y line. This prevents the pulse on the Y line from having any effect on the addressed core. Note that the pulse on the inhibit line goes through all of the cores on the same plane, so it adds to the pulses on the X select lines. For all of the non-selected X lines, where there is no pulse to add to, the amplitude is not enough to flip the cores. For the selected X line, the amplitude exactly cancels the pulse on that line, so again, no cores are flipped.

If wiring three wires through each core was difficult, wiring four wires through each core was horrible, particularly when two of those four had to pass through every core in the plane along different paths.

Combining sense and inhibit: Eventually, the need for the wildly complex threading of the sense line was eliminated by combining the roles of the sense and inhibit lines, so that only 3 lines passed through each core and two of them were in parallel for most of their trip. This required more complex drivers on the combined sense-inhibit lines, and it required sense amplifiers that were insensitive to the voltages involved in driving the inhibit pulses. The benefits of semi-automated assembly more than paid for this complexity.

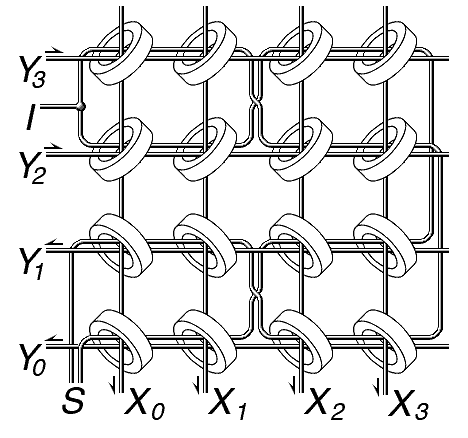
To combine the sense and inhibit lines, the inhibit line was center tapped. Applying an inhibit pulse from the center tap I to the two sense ends, S here, served to inhibit one of the select lines, here shown as Y lines. If the inhibit terminal I is disconnected, a select pulse selects one core and if it changes its state, it induces a differential pulse between the two sense terminals S. The key to making this work isto exchange the two sense-inhibit lines in the middle of each row so that the select pulse parallel to each half run of the sense/inhibit line induces an equal and opposite pulse in the next half run. U.S. Patent 3,329,940, issued July 4, 1967 to Creighton Barnes, et. al. of North American Aviation appears to have pioneered the combining of sense and inhibit lines, while U.S. Patent 3,711,839, granted Jan. 16, 1973 to Victor Sell and M.S. Alvi of Ampex Corporation covers the "double herring-bone" compact core arrangement illustrated here.