a) LEACC R0,R3,-THIS __CMPI R3,THIS__________________
b) LEACC R4,R5,THESE __ADDI R4,R5,THESE______________
c) SUB R0,R6,R7 __CMP R6,R7____________________
d) SUB R8,R0,R9 __NEG R8,R9____________________
e) MOVECC R0,R10 __TESTR R10______________________
1 in 4 got all of these. 1 in 2 got at least one of these. The first one was the hardest. Only one earned no credit at all. Among the weaker students, many made errors suggestive of having spent little time writing assembly language code for the Hawk; this is consistent with the poor overall performance of this class on programming assignments.
a) –1010 ___11110110________________ (scratch space)
b) +2010 ___00010100________________
c) –5010 ___11001110________________
d) +10010 ___01100100________________
e) –12010 ___10001000________________
1 in 2 did perfect work. The errors made by the remainder are somewhat distressing. 1 in 4 could earned no credit on part b. 1 in 7 were off by one on negative numbers, while 1 in 10 negated all of the values.
MACRO ALLOC =n
. = . + n
ENDMAC
We could use this to build the activation record for INTTOS from the posted solution to MP5:
LC = . . = 0 RETAD: ALLOC 4 R8SV: ALLOC 4 ; save locationf for R8 to R10 R9SV: ALLOC 4 R10SV: ALLOC 4 ___ARSIZE = .__________________ ___. = LC_________________
A Problem: Fill in the final 2 lines needed to make this work. (1 point)
1 got this. 1 in 2 earned partial credit by attempting to set ARSIZE but failing to reset the location counter to its original value. Most of those who attempted to set ARSIZE set it incorrectly. Over 1 in 3 earned no credit. Many of these seem to have applied shotgun approaches, filling in blanks with random assembly directives such as ALIGN or EXT.
1000: D4F5F3F4 _________MOVE R4,R3_________
1004: 02025455 _____L: LOADS R5,R4_________
1008: FB00C114 _________EXTB R5,R5,R4______
100C: B1F04323 _________BZS Q_____________
_________ADDSI R4,1__________
_________BR L_____________
_____Q: SUB R3,R4,R3______
_________JUMPS R0,R1_________
a) Convert it back to SMAL Hawk assembly language in the spaces to the right above. The blank space between the code and the answer blanks is scratch space: (2 points)
1 in 5 did well. Among those earning partial credit, 1 in 7 were penalized for failure to figure out the branch displacements, and several reversed the order of all of the halfwords. Both of these errors made it difficult to earn any credit on part b). 1 in 3 earned no credit, and most of those left the problem largely blank.
Given that this was an open-book exam and the Hawk manual has an appendix giving the instructions in reverse numerical order by opcode, this problem is basically clerical work, but it requires that the students understand that the Hawk computer is a low-byter or littleendian machine, and it requires that the student understand hexadecimal.
b) What registers does it expect parameters in, what registers does it alter, and what does it return in what registers? Use a style appropriate for subroutine header comments. (2 points)
______Expects R3 - pointer to a null-terminated string________________ ______Uses R4 - temporary pointer used to traverse string__________ _______________R5 - successive characters of the string________________ ______Returns R5 - string length______________________________________ _______________________________________________________________________
1 in 10 got this, An additional 1 in 7 correctly identified the registers that were used but did not explain how they were used. Among those earning no credit, a remarkable number made statements about register usage after having made little progress on part a). In general, statements about register usage were graded in terms of the answer given to part a).
a) LOAD R8,R2,R8SAVE ___register mode, indexed mode__________________
b) LOAD R3,TRANSLATE ___register mode, pc-relative mode______________
c) LIS R4,' ' ___register mode, immediate mode________________
d) BZR RELOOP ___pc-relative mode_____________________________
e) LOADS R3,R4 ___register mode, short-indexed mode____________
1 in 4 earned full credit. An equal number earned no credit, frequently for giving answers that strongly suggested that they had no clue what the phrase addressing mode referred to. Among those earning partial credit, PC-relative mode was the most frequently remembered.
Nobody mentioned that the first operand of many instructions is always a register mode instruction, but this was not penalized.
A problem: Write SMAL Hawk code to rotate R3 10 bits right. R4 and up are available. (1.5 points)
________MOVESL R4,R3,11_______________________________________________ ________SL R4,11__________________________________________________ ________SRU R3,10__________________________________________________ ________OR R3,R4__________________________________________________ _______________________________________________________________________
None did perfectly. 1 in 3 earned good partial credit for answers that used shift counts over 16. Because the actual shift count needed is 22, this must be divided into 2 shift instructions.
1 in 3 wrote solutions that involved loops, and 1 in 3 (many the same) added large numbers of unnecessary instructions. 1 in 3 earned no credit, but only one left this blank. Several gave nonsense answers, for example, copying one of the optimal code sequences for multiplying by a constant, something unrelated to the assignment except that it also involves shifting.
It is clear that a large fraction of the class has significant difficulty with any computations involving shift operators.
| s | = | sign of mantissa | ||||||||||||||
| exp | = | biased exponent 111 – not a number, infinity if m=0 011 – represents zero 000 – non-normalized values (hidden bit = 0) | |||||||||||||||
| mnt | = | mantissa with hidden bit in 1's place | |||||||||||||||
Convert each of the following numbers in this format to decimal (0.3 points each):
(scratch space)
a)
000001
b) 110010
c) 011100
d) 001000
e) 100010
1/4 earned full credit. Part a was the most difficult, with 3 in 4 earning no credit. Part d was also hard, completely stumping 1 in 3 while another 1 in 3 only got the sign right.
It is noteworthy that this was the same floating point representation used on the second midterm. In general, students who had difficulty with negative numbers in the 2's complement number system had even more difficulty here where the exponent is represented as a biased number with an unnatural bias.
TIMES: ; multiply
; expects: R4 - ier, integer multiplier
; R5 - icand, integer multiplicand
; returns: R3 - ?
; destroys: R6 - loop counter
LIS R6,32
TIMESLP: __________________ ; loop 31 times { ___________
| SRU R3,1 ; R3 = R3 >> 1 |
| SRU R4,1 ; ier = ier >> 1 |
| ADJUST R4,CMSB |
| BCR TIMESEND ; if (C) { |
|_ ADD ___ R3,R3,R5 __ ; ___ R3 = R3 + icand _______|
TIMESEND: ; }
ADDSI R6,-1
BGT TIMESLP ; }
JUMPS R1 ; return
a) What is returned in R3 and R4? (0.5 points)
____R3 holds the most significant 32 bits of the product_______
____R4 holds the multiplier____________________________________
None earned full credit. 1 in 3 earned partial credit for recognizing that R3 ends up holding the product, but not specifying that it's just the high half of the product. Some explicitly said low half, but that is the correct answer for a different multiply algorithm.
There is an error in the code. A number correctly interpreted the result of the error — that the multiplier in R4 ends up unchanged.
It is apparent that many students focused their effort on using the notes to find the closest similar multiply algorithm. The algorithm above is not in the notes, and a correct answer therefore has to rest on reading and understanding the code.
b) What does the C condition code tested by the BCR instructions hold? (0.5 points)
____The least significant bit of the remaining multiplier______
_______________________________________________________________
1 in 5 earned full credit here, and even more earned partial credit for implicating something about R4 or the carry after a shift, without connecting the result to some particular property of the multiplier.
c) If we omit the ADJUST instruction, what is returned in R3 and R4? (0.5 points)
____R3 as in part a, the high half of the product______________
____R4 ends up zero____________________________________________
1 in 10 did well. Several left this blank, and almost 1 in 3 gave answers that verged on nonsense.
d) To speed this code up, we could change the iteration count from 32 to 16. This requires that we unroll the loop. Draw a circle or oval around the block of code that would need to be duplicated above to do this. (0.5 points)
Over 1 in 3 did well. Among those earning partial credit, almost all included the ADJUST and BCR instructions in the block they marked, but some focused on the two shift instructions, and one included the opening LIS instruction that is outside the loop.
STRCPY: ; expects R3 = dst, a pointer to a destination string
; R4 = src, a pointer to a source string
; use R5 = dst'
; R6 = ch
; R7 temp
MOVE R5,R3 ; dst' = dst
STRCLP: ; loop { ___ start of body ___
__ LOADS R6,R4
EXTB R6,R6,R4 ; ch = *src
__ LOADS R7,R5
__ STUFFB R7,R6,R5
STORES R7,R5 ; *dst' = ch
BZS STRCQT ; if (ch == NULL) break
ADDSI R4,1 ; src++
ADDSI R5,1 ; dst'++ ____ end of body ____
BR STRCLP
STRCQT: ; }
JUMPS R1 ; return dst -- was always in R3
a) On a 4-stage pipelined Hawk, how many delay slots are in the loop body? (1.5 points)
____6______________(2 at each point marked above)______________
1 in 5 did well, 1 in 4 said 3 for half credit, while 1 in 7 said 4 and an equal number said 2. A few gave very odd answers earning no credit. One, in particular, stood out by suggesting that there were 48 delay slots.
b) Rewrite the body to minimize the number of delay slots. Use R1 if needed. Omit comments. (2 points)
______LOADS R6,R4____________________________________________
______LOADS R7,R5____________________________________________
______EXTB R6,R6,R4_________________________________________
______ADJUST R4,PLUS1_________________________________________
______STUFFB R7,R6,R5_________________________________________
______STORES R4,R5____________________________________________
______BZS STRCQT___________________________________________
______ADDSI R5,1_____________________________________________
Just one did perfect work here, while 1 in 4 came close, typically either not noticing the opportunity to replace ADDSI with ADJUST, allowing it to be moved up without destroying the condition codes, or not noticing the need to preserve the condition codes and moving up the ADDSI.
The solution above has 4 delay slots, and there are several others that do this. Some students added gratuitous instructions that filled delay slots while adding code. Delay slots filled this way were not counted as having been eliminated.
Several students left this blank or simply copied the original code, adding errors or gratuitous changes in register use. These received no credit. Among the odd answers, one apparently could not identify the body being referred to.
c = a b
d = a c
e = c b
f = d e
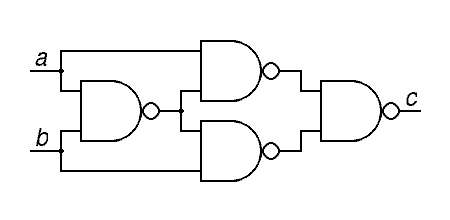 a)
Draw the circuit in the space to the left
(1 point)
a)
Draw the circuit in the space to the left
(1 point)
b) Fill in this truth table: (1 point)
| a | b | c | d | e | f |
| _0_ | _0_ | _1_ | _1_ | _1_ | _0_ |
| _0_ | _1_ | _1_ | _1_ | _0_ | _1_ |
| _1_ | _0_ | _1_ | _0_ | _1_ | _1_ |
| _1_ | _1_ | _0_ | _1_ | _1_ | _0_ |
Over half the class did perfectly — this was probably the easiest problem on the exam. The most common problems were clerical errors, although in some cases, these were almost certainly caused by a generally sloppy approach to the problem. There were a few serious errors involving misreading the overbar notation.