a) He built the Turing Machine, the first practical computer.
b) He was the first cryptographer to attack the German enigma cypher.
c) His ACE was the first commercially successful electronic computer.
d) All of the above.
e) None of the above.
Note that this question was promised on the Midterm but accidentally omitted. It is offered here instead. (0.2 points)
None are true. The Turing machine was never intended as a practical computer; rather, it was a theoretical way of reasoning about computability. Turing did indeed attack the Enigma cypher, but he was not the first. The bombe built at Bletchley Park was preceeded by the polish bomba built at the Polish Cypher Bureau. The ACE was, at best, a prototype. It's commercial successor, the DEUCE, came out in 1955, by which time both the UNIVAC I and the IBM 701 were both in production and each had sales figures of 18 or more machines. The above took a few minutes of web searching using Wikipedia as a guide.
Background: Consider this function:
int index( char s[], char ch ) {
int i = 0;
while ((s[i] != NUL) && (s[i] != ch)) i = i + 1;
if (s[i] == NUL) i = -1;
return i;
}
This function returns -1 if the character ch is not in the null-terminated string s, and it returns the index of the character in the string if it is there. Note that s is a pointer to the first character in the string.
Background: Write reasonably good SMAL Hawk assembly code for this function. Note that it can be coded without an activation record using only registers 3 to 7. The focus here is on string processing. (1.3 points)
INDEX: ; expects R3 = s -- pointer to a null terminated string ; R4 = ch -- a character ; returns R3 = i, index in s such that s[i] = ch ; or -1 if ch does not occur in s ; uses R5 = temporary for extracting characters from s ; R6 = i during computation LIS R6,0 ; i = 0 INDLP: ; do { -- loop with two exit conditions LOADS R5,R3 EXTB R5,R5,R3 BZS INDMISS ; if (s[i] == 0) break -- ch not found CMP R5,R4 BEQ INDHIT ; if (s[i] == ch) break -- found! ADDSI R6,1 ; i = i + 1 ADDSI R3,1 ; -- address of s[i] advanced also BR INDLP ; } while (true) INDMISS: ; if (s[i] == 0) { LIS R3,-1 JUMPS R1 ; return -1 INDHIT: ; } MOVE R3,R6 JUMPS R1 ; return iStudents were not expected to write code this optimal, but many students did write reasonably good code. Reasonably readable comments were less common.
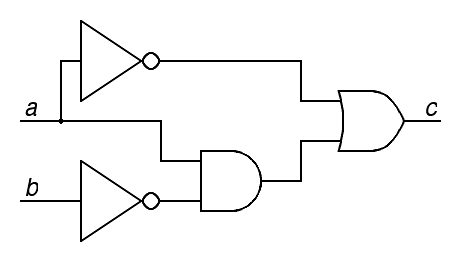
|
a) Give an algebraic expression for c as a function of a and b using the operators + and · (mathematical symbols for addition and multiplication) for the Boolean or and and operators, and using overbar for not. Do not try to optimize the function yet. (0.5 points)
c = a + ( a · b )
b) Give a truth table for the function, showing the values for the inputs a and b, the intermediate values a and b, along with any other intermediate values useful to computing the output, and finally, the output c. (0.5 points)
a b a b a·b c 0 0 1 1 0 1 0 1 1 0 0 1 1 0 0 1 1 1 1 1 0 0 0 0
c) Give a compact optimized algebraic expression for c as a function of a and b using the same notation as required for part a). Note that you may find the truth table from part b) very helpful in this exercise. (0.5 points)
The following two answers are equivalent under DeMorgan's laws, although the first is probably a little bit more intuitive (the nand function):
c = a · b
c = a + b