Assignment 7, due Mar 14

On every assignment, write your name legibly as it appears on your University ID card! Homework is due on paper at the start of class on the day indicated (usually Friday). Exceptions will be made only by advance arrangement (excepting "acts of God"). Late work must be turned in to the TA's mailbox (ask the CS receptionist in 14 MLH for help). Never push homework under someone's door!

1. A quick question: Which of the following are true statements about Alan Turing:

   a) He built the Turing Machine, the first practical computer.

   b) He was the first cryptographer to attack the German enigma cypher.

   c) His ACE was the first commercially successful electronic computer.

   d) All of the above.

   e) None of the above.

   Note that this question was promised on the Midterm but accidentally omitted. It is offered here instead. (0.2 points)

2. Background: Consider this function:

   int index( char s[], char ch ) {
           int i = 0;
           while ((s[i] != NUL) && (s[i] != ch)) i = i + 1;
           if (s[i] == NUL) i = -1;
           return i;
   }
   

   This function returns -1 if the character ch is not in the null-terminated string s, and it returns the index of the character in the string if it is there. Note that s is a pointer to the first character in the string.

   Background: Write reasonably good SMAL Hawk assembly code for this function. Note that it can be coded without an activation record using only registers 3 to 7. The focus here is on string processing. (1.3 points)

3. Background: Consider the logic circuit to the right:

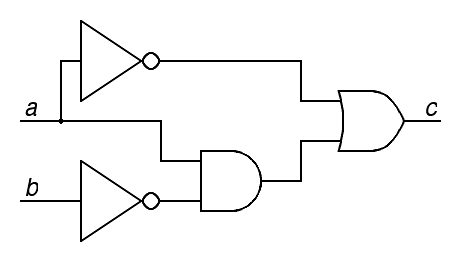
   a) Give an algebraic expression for c as a function of a and b using the operators + and · (mathematical symbols for addition and multiplication) for the Boolean or and and operators, and using overbar for not. Do not try to optimize the function yet. (0.5 points)

   b) Give a truth table for the function, showing the values for the inputs a and b, the intermediate values a and b, along with any other intermediate values useful to computing the output, and finally, the output c. (0.5 points)

   c) Give a compact optimized algebraic expression for c as a function of a and b using the same notation as required for part a). Note that you may find the truth table from part b) very helpful in this exercise. (0.5 points)