9. Beyond Add and Subtract.
Part of
CS:2630, Computer Organization Notes
|
In the previous chapter, we discussed the details of how computers
do binary addition and subtraction. With that background, we are
now ready to explore more complex arithmetic operations. Integer
multiplication and division are primitive enough that many computers
implement them in hardware, but complex enough that in many other
very successful computers, they are entirely done by software. This
introduces an important subject, the engineering tradeoffs that lead
to the decisions about which features to implement directly in hardware
and which are more economically done in software.
Before discussing efficient machine implementations of multiplicaton and
division, whether in hardware or software, we must back off and
discuss, first, the pencil and paper algorithms in decimal, and then how
we can do these in binary.
Consider the problem of multiplying 128 times 512
in decimal. Here is how you were probably taught to work this problem
out using pencil and paper:
| 1 | 2 | 8 | multiplicand | |||
| × | 5 | 1 | 2 | multiplier | ||
| | ||||||
| 2 | 5 | 6 | partial product 2 × 128 | |||
| 1 | 2 | 8 | partial product 1 × 128 | |||
| + | 6 | 4 | 0 | partial product 5 × 128 | ||
| | ||||||
| 6 | 5 | 5 | 3 | 6 | product | |
The worksheet for carrying out a decimal problem as shown above
is actually a trace of the execution of an algorithm. This algorithm
proceeds by first
multiplying the multiplicand by each digit of the multiplier to create a list
of partial products. Each partial product is written shifted over one place
relative to its predecessor, so that it's least significant digit is under
the corresponding digit of the multiplier. This shifting is equivalent to
multiplying the multiplicand by ten before computing each partial product.
At the end, the partial products are all added to compute
the product.
The statement of this algorithm does not depend on the number base being used. Thus, we can use this exact same algorithm in base 16 or in base 8 or even in base 2. The hard part of this algorithm in decimal is multiplying the multiplicand by the digits of the multiplier. To do this, the typical elementary school student must memorize the multiplication tables for base 10. The base 2 multiplication table is far simpler.
a) Write code, in C, C++ or Java, to multiply two positive integers using the decimal algorithm you'd use with pen and paper. With each iteration, you should end up accumulating one partial product, multiplying the multiplicand by 10, and dividing the multiplier by 10. You can extract the least significant digit of the multiplier using the mod operator, written as % in these languages. Multiply this times the multiplicand to compute the partial product. It may seem silly to use both multipication and division in order to multiply, but the only divisor used is 10, and the only multipliers are from 0 to 10, so this code uses a limited set of operations to implement a much more general operation.
To multiply two binary numbers using pencil and paper, we use exactly the same multiplication algorithm we would use in decimal, but we do it using binary arithmetic. Consider, for example, the problem of multiplying 10010 by 1010. In binary, this is 11001002 times 10102; if we work the problem using pencil and paper, we get this:
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | = 100 | multiplicand | ||||
| × | 1 | 0 | 1 | 0 | = 10 | multiplier | ||||||
| | ||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | = 0 × 100 | partial products | ||||
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | = 1 × 100 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | = 0 × 100 | |||||
| + | 1 | 1 | 0 | 0 | 1 | 0 | 0 | = 1 × 100 | ||||
| | ||||||||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | = 10 × 100 | = 1000 | |
This workshet for binary multiplication shows the partial products computed by multiplying the multiplicand by each bit of the multiplier. Each partial product is shifted over so it's least significant bit is under the corresponding multiplier bit, and at the end, the partial products are added.
It is not difficult to reduce this paper-and-pencil algorithm to machine code for the Hawk machine. The first step in such a reduction is to work it out in a high-level language like C or Java:
unsigned int multiply( unsigned int multiplier, unsigned int multiplicand ) {
unsigned int product = 0;
while (multiplier != 0) {
if ((multiplier & 1) != 0) {
product = product + multiplicand;
}
multiplier = multiplier >> 1;
multiplicand = multiplicand << 1;
}
return product;
}
|
In the above, we have shifted the multiplicand one place left on each iteration so we can add it in as a partial product when the corresponding multiplier bit is nonzero. For each iteration, we shift the multiplier one place right so that we can always check the least significant bit instead of testing a different bit for each iteration. We test the bit by using the bitwise and operator of C to mask out all but the least significant bit. Here is exactly the same code using operators many be more familiar:
unsigned int multiply( unsigned int multiplier, unsigned int multiplicand) {
unsigned int product = 0;
while (multiplier != 0) {
if ((multiplier % 2) != 0) {
product = product + multiplicand;
}
multiplier = multiplier / 2;
multiplicand = multiplicand * 2;
}
return product;
}
|
Here, we substituted multiplication and division by two for shifting, and we tested to see if the multiplier was even or odd by checking the remainder after division by two. Using multiplicaiton and division to implement multiplication is not useful on a machine without multiply hardware, but good compilers frequently substitute shift and bit manipulation for multiplication and division by powers of two.
This algorithm is ancient and has been repeatedly rediscovered. It is sometimes called the the Russian peasant algorithm or Egyptian multiplicaton after two of the many folk origins for the method.
The first multiply code given above only used operators available on the Hawk machine. For the left and right shifts, where C uses << and >>, we have SL and SRU, and for the and operator, where C uses &, we have AND. These let us rewrite the C code as follows:
MULTIPLY:
; expects R3 = multiplier
; R4 = multiplicand
; uses R5 = temporary copy of multiplier
; R6 = temporary used for anding with one
; returns R3 = product
MOVE R5,R3 ; -- move the multiplier
CLR R3 ; product = 0;
MULTLP:
TESTR R5
BZS MULTLX ; while (multiplier != 0) {
LIS R6,1
AND R6,R5
BZS MULTEI ; if ((multiplier & 1) != 0) {
ADD R3,R3,R4 ; product = product + multiplicand;
MULTEI: ; }
SRU R5,1 ; multiplier = multiplier >> 1;
SL R4,1 ; multiplicand = multiplicand << 1;
BR MULTLP
MULTLX: ; }
JUMPS R1 ; return product;
|
The above code takes either 8 or 9 instructions per iteration of the loop, depending on whether the bit of the multiplier is one or zero. The code is written in what might be called a bone-headed style, making as little use of auxiliary information as possible. In fact, a little study of the shift instructions leads quickly to some significant optimizations.
As a general rule, optimization is something to leave for last, but the very first candidates for optimization are those routines that are called repeatedly from many different applications. The subroutines for performing arithmetic operations that are not performed in hardware are excellent candidates for this. Clearly, the speed of the multiply routine could have a central effect on a wide variety of applications. Therefore, we will explore the possibility of optimizing this routine with more interest than we would have considered optimizing of other less frequently used routines.
All shift instructions on the Hawk set the condition codes, so after doing the SRU instruciton at the end of the loop, we can test to see whether the multiplicand has been reduced to zero, eliminating the need for the TESTR instruction at the top of the loop in all but the first iteration. We can test even more than this, because the shift operators also set the carry bit in the condition codes to report on the bits shifted out of the operand, so the SRU instruction, with a shift count of one also tells us if the operand was even or odd prior to the shift. This leads us to the following faster unsigned multiplication code:
MULTIPLY:
; expects R3 = multiplier
; R4 = multiplicand
; uses R5 = temporary copy of multiplier
; returns R3 = product
MOVE R5,R3 ; -- move the multiplier
CLR R3 ; product = 0;
TESTR R5
BZS MULTLX ; if (multiplier != 0) {
MULTLP: ; do {
SRU R5,1 ; multiplier = multiplier >> 1;
BCR MULTEI ; if (multiplier was odd) {
ADD R3,R3,R4 ; product = product + multiplicand;
MULTEI: ; }
SL R4,1 ; multiplicand = multiplicand << 1;
TESTR R5
BZR MULTLP ; } while (multiplier != 0);
MULTLX: ; }
JUMPS R1 ; return product;
|
This improved version takes either 5 or 6 instructions per iteration, so it will run about 30% faster than the original code. Furthermore, it uses one less register because of the way the multiplier bits are tested. One cost of this optimization is that it is harder harder to write C-like comments because languages C no longer accurately captures what some of the above code does. This code is about as good as you would normally hope for from decent assembly language code, but further optimizations are possible. Consider the following:
MULTIPLY:
; expects R3 = multiplier
; R4 = multiplicand
; uses R5 = temporary copy of multiplier
; returns R3 = product
MOVE R5,R3 ; -- move the multiplier
CLR R3 ; product = 0
TESTR R5
BZR MULTLE ; go loop if nonzero multiplier
JUMPS R1 ; return product if not
MULTLP: ; continue main multiplication loop
SL R4,1 ; multiplicand = multiplicant << 1
MULTLE: ; loop entry point
SRU R5,1 ; multiplier = multiplier >> 1
BCS MULADD ; if (multiplier was odd) go add
BZR MULTLP ; continue loop if multiplier nonzero
JUMPS R1 ; return product;
MULADD: ; annex to multiplication loop
ADD R3,R3,R4 ; product = product + multiplicand;
TESTR R5
BZR MULTLP ; continue loop if multiplier nonzero
JUMPS R1 ; return product;
|
This new version takes either 4 or 6 instructions per iteration, sometimes faster than the previous code, and duplicating the return instruction saved a few instructions per call. Whether these changes actually lead to performance improvement on a real CPU must be determined by empirical testing. Together, these changes destroy the clean control structure of the original, blocking use of a high-level language comment style. Optimizations that reduce code readability are only justified when performance is critical.
This particular optimization is working toward a dead-end. Just as the key to fast string operations on the Hawk is to work with blocks of characters, the key to fast multiplication is is to operate in a higher number base than 2. For the Hawk, base 16 works well. Chapter 13 of the Hawk manual gives unsigned integer multiply code that has a worst-case cost of 2.8 instructions per bit to compute a 32-bit product; this code is even less readable than any of the above code, but if speed is the object, it is a clear winner.
b) Flip coins to generate a random 8-bit multiplicand and a random 4-bit multiplier. Multiply them using the paper-and-pencil binary multiplication algorithm, then check your work by converting your numbers to decimal.
c) Rewrite the binary multiplication algorithm in C to work in base 16. This involves only extremely small changes to the code given above: You must allow for multiplier digits to have more than 2 possible values (zero and one) and you must change all references to the radix from 2 to 16 (or alternately, change all one-bit shifts to 4-bit shifts).
d) What happens with the Hawk binary multiplication code if you multiply numbers together that generate a result of 232 or greater. For example, what happens if you compute 125,000 squared using this code? 125,000 is near 217, so the answer should be near 234.
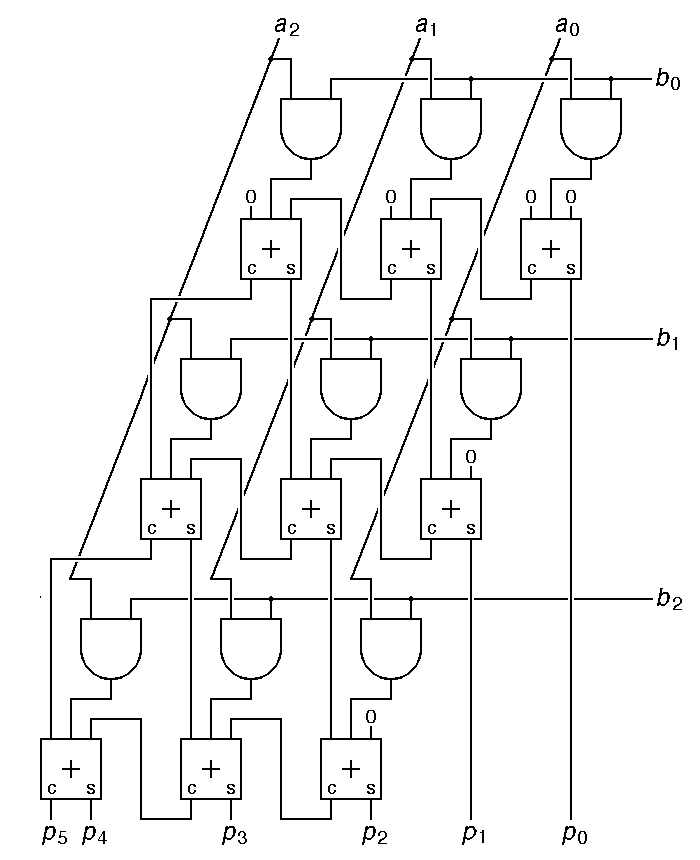
In the binary multiply code given above, multiplying two 32-bit numbers took 32 shifts and up to 32 adds. We can do all of this in parallel using 31 adders. Here is how the parallel scheme works for two 3-bit numbers a and b to give the 6-bit product p.

|
This circuit is not optimized. The top row of adders can be eliminated, and the rightmost adder in each row can be replaced with a half-adder. The total number of logic gates required is estimated as follows:
| A single full adder | 12 |
| 32 bits per word | × 32 |
| gates per 32-bit adder | 384 |
| 31 adders to add 32 partial products | × 31 |
| Subtotal: Cost of adding partial products | 11904 |
| and gates to compute a partial product | 32 |
| 32 partial products | × 32 |
| Subtotal: Cost of computing partial products | 1024 |
| | |
| Estimated gate count for fast multiplication | 12928 |
This is rather discouraging. 12000 gates is more than enough to build a whole CPU. In contrast, it takes under 2000 gates to build the entire Hawk ALU and shifter, logic that is central to most computations. Adding one additional function by using seven times the amount of harware is not a very economical approach to computer design. Therefore, few but the very fastest computers include such high-speed brute-force multipliers.
Most computers with multiply hardware do multiplication using the same arithmetic-logic unit as they use for addition, cycling the data through the arithmetic-logic unit once per partial product. This is why, when you look at data for the speed of the various instructions on real computers, it is quite common to find that integer multiplication is 10 or more times slower than integer addition. On the Intel Pentium, introduced in 1993, the hardware could execute two integer add instructions in parallel in 1/10th the time it took to execute one integer multiply instruction.
Because of the slow speed of hardware multiplication on most computers, compiler writers have long been urged to avoid using multiply instructions whenever they can find a short sequence of shift and add instructions that will do the same thing. These optimizations can be expressed quite easily in languages like C, C++ or Java:
| original | substitution | |||
|---|---|---|---|---|
| a * 2 | a << 1 | |||
| a * 3 | (a << 1) + a | |||
| a * 4 | a << 2 | |||
| a * 5 | (a << 2) + a | |||
| a * 6 | ((a << 1) + a) << 1 | |||
| a * 7 | (a << 3) - a | |||
| a * 8 | a << 3 | |||
| a * 9 | (a << 3) + a | |||
| a * 10 | ((a << 2) + a) << 1 |
Don't write this kind of code in your C or Java programs unless your goal is to write code nobody can understand. Let the compiler do the optimization for you. If you are writing in assembly language or writing a compiler, you need to know these optimizations. In addition, if you are trying to write fast code, it is useful to know what good compilers do to your code.
In general there will be one partial product to add for each one in the binary representation of the multiplier, plus the shift operators needed to align the partial products. On the Pentium, where integer multiply took about ten times longer than a shift or an add, good compilers use shift and add instructions for constant multipliers with five or fewer one bits.
Sometimes, we can do better, as illustrated in the case for multiplication by seven in the above table. There, we could have used (((a<<1)+a)<<1)+a, adding three terms that correspond to the 3 one bits in the multiplier. Instead, in the table above, we multiplied by eight and then subtracted.
Another trick we can use is to factor a number and then multiply by each of the factors. For example, to multiply by 100, we could multiply by 10 twice, or we could multiply by 5 twice and then multiply by 4.
| a * 100 | (((a << 1) + a) << 3) + a) << 2 |
| a * 10 * 10 | t = ((a << 2) + a) << 1;
((t << 2) + t) << 1 |
| a * 5 * 5 * 4 | t = ((a << 2) + a);
((t << 2) + t) << 2 |
Which of these will be fastest on a particular machine? In general, examining high level language code only allows an educated guess. Classical computer architectures use roughly one instruction per operator, and when register to register operations are available, assignment to the temporary variables used for intermediate results may be free. For such machines, what matters is the total count of operators in the expression. This leads us to guess that binary multiplication by 100 will tie with multiplying by 5 twice and then by 4, taking 3 shifts and 2 adds, while Multiplying by 10 twice in a row will be slower, taking 4 shifts and 2 adds.
Our first conclusion from the above estimates of performance is that all of the above multipliction methods will be noticably faster than a hardware multiply on a machine like the Pentium. The numbers suggest that multiplication by ten twice in sequence might be a bit slower, but with a difference of just one operation between our fastest and slowest estimates, what we should really conclude is that these alternatives are all similar.
To reduce these to machine code, we must look at the available shift instructions. The Hawk has two left shift instructions, MOVSL, which does a register to register move plus a shift, and ADDSL, which shifts the contents of one register and then adds another register to it. The SL assembly language opcode is really ADDSL with the second register set to zero to mean add nothing. Similar shift and add instrucitons are included in several architectures designed after the late 1970's; in the early 1980's, a group at Hewlett Packard was the first to describe, in detail, how to fully exploit these instructions. Here is how we can use these on the Hawk:
| SL | R3,1 | ; R3 = R3 * 2 = R3 << 1 |
| ADDSL | R3,R3,1 | ; R3 = R3 * 3 = (R3 << 1) + R3 |
| SL | R3,2 | ; R3 = R3 * 4 = R3 << 2 |
| ADDSL | R3,R3,2 | ; R3 = R3 * 5 = (R3 << 2) + R3 |
| SL ADDSL |
R3,1 R3,R3,1 |
; R3 = R3 * 6 = R3 * 2 * 3 |
| NEG ADDSL |
R1,R3 R3,R1,3 |
; R3 = R3 * 7 = (R3 << 3) - R3 |
| SL | R3,3 | ; R3 = R3 * 8 = R3 << 3 |
| ADDSL | R3,R3,2 | ; R3 = R3 * 9 = (R3 << 3) + R3 |
| SL ADDSL |
R3,1 R3,R3,2 |
; R3 = R3 * 10 = R3 * 2 * 5 |
The Hawk ADDSL instruction allows us to multiply by a wide range
of small constants in just one or two instructions. Multiplication by
11 takes three instructions, but there are also three instruction sequences
to multiply by all larger integers up to 38 and for many above that.
Many of these
are documented in Chapter 10 of the Hawk CPU manual.
e) Convert each of the three algorithms given above for multiplication by 100 into tightly coded Hawk instruciton sequences that compute R3 = R3 * 100. Rank them in order of speed. (Note that there could be a tie, and assume you can use R1 as an auxiliary register.)
f) Write hawk code to multiply R3 by 55.
g) Write hawk code to multiply R3 by 60.
h) Write hawk code to multiply R3 by 47.
i) What is the smallest constant multiplier for the Hawk that requires a 4-instruction sequence? (All the sequences given in the Hawk manual are only 3 instructions long.).
We have now covered enough ground to understand why the Hawk and a few other modern high performance 32-bit computer architectures have no hardware support for integer multiplication. The answer lies in the frequency with which application programs actually need to multiply. Large scale studies of real programs show that the vast majority of the multiply operations in most real code involve multiplication by small constants. multiplication of a variable by a variable is much rarer.
Because we have short fast sequences of instructions to multiply by common small constants, and because we have relatively fast subroutines for the rare occasions when two variables must be multiplied, there is little advantages to a hardware implementation of multiplication.
Suppose hardware was so cheap that we could easily afford to dedicate thousands of gates to fast multiply hardware. An important engineering question is, what competing uses we could make of that much hardware? Fast hardware multiplication might speed up a computation by a few percent. Can we use our resources to better effect somewhere else in the CPU? Would we be better off building a second CPU, potentially doubling the speed of the computer? Would we be better off with more registers or a bigger cache memory to speeds up every memory reference?
To divide a number by another using pencil and paper, we use the classical long division algorithm traditionally taught in elementary school. As with pencil and paper multiplication, this division algorithm involves building and filling in a work sheet as the computation progresses. Consider the problem of dividing 128 into 65538:
| 5 | 1 | 2 | quotient | |||||||
| | ||||||||||
| divisor | 1 | 2 | 8 | ) | 6 | 5 | 5 | 3 | 8 | dividend |
| – | 6 | 4 | 0 | = 5 × 128 | ||||||
| | ||||||||||
| 1 | 5 | 3 | 8 | |||||||
| – | 1 | 2 | 8 | = 1 × 128 partial products | ||||||
|
| ||||||||||
| 2 | 5 | 8 | ||||||||
| – | 2 | 5 | 6 | = 2 × 128 | ||||||
|
| ||||||||||
| 2 | remainder | |||||||||
Long division involves a series of subtractions from the dividend. The values subtracted are called partial products because they are the partial products we would add in multiplying the quotient by the divisor to get the dividend (less the remainder). You can verify this by comparing with the multiplication problem given earlier in this chapter. Each partial product is the product of a quotient digit and the divisor. The hard part of decimal long-division is estimating the quotient digits. If we do this in binary, that is much easier because there are only two choices for each digit.
The classic way to divide one binary number by another is to shift both the quotient and the dividend left at each step instead of holding them statically and shifting the partial products right. We start with the 32-bit dividend in the least significant 32 bits of a 64-bit register, then after 32 shift-and-subtract steps, the remainder is in the high 32 bits and the quotient in the low 32 bits. We can write this in C on a machine that supports the type int using 32 bits and long int using 64 bits:
unsigned int divide( unsigned int dividend, unsigned int divisor ) {
unsigned long int remquot = dividend;
unsigned long int divisorhigh = divisor << 32;
unsigned int remainder, quotient, i;
for (i = 0; i < 32; i++ ) {
remquot = remquot << 1;
if (remquot >= divisorhigh) {
remquot = (remquot - divisorhigh) + 1;
}
}
remainder = remquot >> 32; /* the upper 32 bits */
quotient = remquot & 0xFFFFFFFF; /* the lower 32 bits */
return quotient;
}
|
This short but difficult bit of code computes both the remainder and the quotient, no matter which is needed. The C version cannot return both, but returning both is easy in assembly language.
To write this for the Hawk, we need a way to shift a 64-bit number one place left. On the Hawk and most other machines, shifts use the carry bit to show the last bit shifted out. After shifting left one bit, carry holds the old sign bit. Therefore, for a long left shift, we can shift the two halves separately using carry to bridge the gap. There are many ways to do this:
SL R4,1 ; high = high << 1
SL R3,1 ; low = low << 1
BCR NOCARRY ; if (C == 1 (the bit shifted out)) {
ADDSI R4,1 ; high = high + 1
NOCARRY: ; }
|
SL R4,1 ; high = high << 1
SL R3,1 ; low = low << 1
ADDC R4,R0 ; high = high + 0 + C (the carry bit)
|
SL R3,1 ; low = low << 1
ADDC R4,R4 ; high = high + high + C
|
The first version above uses a conditional branch to
test the carry after shifting the low half of the number,
and then explicitly adds one to the high half if needed.
The Hawk has a special instruction to add
the carry to the sum of two registers,
ADDC. The second version uses this
to replace the conditional branch and incrment.
Note that adding a number to itself shifts it one place, so
ADDC can shift as it adds in the carry.
This gives the final and fastest version.
For completeness, here is a fast 64-bit right-shift
using a special instruction called ADJUST:
SRU R3,1 ; low = low >> 1
SRU R4,1 ; high = high >> 1
ADJUST R3,CMSB ; low = low + (C << 31)
|
These high-precision shifts give us the
tools we need code a divide algorithm on the Hawk:
DIVIDEU:
; expects R3 = dividend on entry
; R5 = divisor, unchanged on return
; uses R6 = i, a loop counter
; returns R3 = quotient
; R4 = remainder
; quotient = dividend
CLR R4 ; remainder = 0
LIS R6,32 ; i = 32
DIVLP: ; do {
SL R3,1 ; quotient = quotient << 1, sets C bit
ADDC R4,R4 ; remainder = (remainder << 1) + C
CMP R4,R5
BLTU DIVNO ; if (remainder >= divisor) {
SUB R4,R4,R5 ; remainder = remainder - divisor
ADDSI R3,1 ; quotient = quotient + 1
DIVNO: ; }
ADDSI R6,-1 ; i = i - 1;
BGT DIVLP ; } while (i > 0)
JUMPS R1 ; return
|
Here, we have referred to the high half of our 64-bit working register
as the remainder and the low half as the quotient, because that is what they
eventually hold. As the code iterates, bits of the dividend are
shifted out of the quotient register into the remainder before each
partial product is subtracted.
We made one change in the organization of the loop when we moved from the original C code to the code given above. Instead of making the loop count up from 0 to 32, we started the loop control variable at 32 and decremented to zero. This optimization allowed us to test for termination by checking the condition codes after the decrement, eliminating the need for a compare instruction in the loop body.
There is an additional optimization that can be made to any loop, called loop unrolling. In the general case, loop unrolling involves replicating the body of a loop, including any tests for loop termination. This enlarges the loop body and eliminates branch instruction per replica. When unrolling a definite loop, where the number of repeats of the loop body divides evenly into the number of iterations, we can save even more by omitting duplicate tests for loop termination.
In general, loop unrolling has its biggst impact on loops with a very small
body, and the divide algorithm given here is a good example.
Here is the result, applied to the above C code:
unsigned int divide( int dividend, unsigned int divisor ) {
unsigned long int remquot = dividend;
long int remainder, quotient;
int i;
for (i = 0; i < 16; i++ ) {
remquot = remquot << 1;
if (remquot >= (divisor << 32)) {
remquot = (remquot - (divisor << 32)) + 1;
}
remquot = remquot << 1;
if (remquot >= (divisor << 32)) {
remquot = (remquot - (divisor << 32)) + 1;
}
}
remainder = remquot >> 32;
quotient = remquot & 0xFFFFFFFF;
return quotient;
}
|
Unrolling the loop one step cuts the number of iterations to 16, eliminates half of the instructions used to increment and test the loop counter and half of the branch instructions back to the loop top. Unrolling the loop 4 steps cuts the number of iterations to 8 while halving the overhead yet again. Unrolling the loop a full 32 times would entirely eliminate the loop control variable and related branch instructions at the expense large-scale duplication of the loop body.
j) Write Hawk code for a 96-bit left shift and for a 96-bit right shift, storing the operand in registers 3, 4 and 5, least significant 32-bits first.
k) Write a new version of the Hawk division code given here with
the loop body unrolled one step as in the C code given above.
The most obvious way to handle signed multiplication and division is to
remember the signs of all the operands and then take their absolute values
beforehand. After computing the product of the absolute values, the
result should then be negated if the operands were of opposite signs.
This is illustrated here for multiplication, but it is equally straightforward
for division.
int signed_multiply( int multiplier, int multiplicand ) {
int product_negative = FALSE;
int product;
if (multiplier < 0) {
multiplier = -multiplier;
product_negative = ! product_negative;
}
if (multiplicand < 0) {
multiplicand = -multiplicand;
product_negative = ! product_negative;
}
product = multiply( multiplier, multiplicand );
if (product_negative) product = -product;
return product;
}
|
The only problem with this approach is that it is unnecessarily complicated. So long as we use two's complement numbers, we can take advantage of the simple place value interpretation of the binary digits of a two's complement number. For bits 0 to 30 of a 32-bit two's complement number, the weight of bit i is 2i, identical to the weight for a simple binary number. For the most significant bit, the sign bit, the weight is negated, so the weight of the sign bit is –231. This leads to the remarkable fact that, when multiplying two's complement signed integers, the final partial product should be subtracted in order to give the correct correct signed result.
To use this fact, we recode our multiply algorithm to use a definite loop instead of an indefinite loop, doing 31 multiply steps inside the loop and then handling the partial product computed from the sign bit outside the loop, subtracting where all the other partial products were added. Here is an example signed multiply, coded using left shifts for both the multiplier and the product:
MULTIPLYS:
; expects R3 = multiplicand
; R4 = multiplier
; uses R5 = copy of multiplicand
; R6 = i, loop counter
; returns R3 = product
MOVE R5,R3 ; -- move multiplicand
CLR R3 ; product = 0
SL R4,1 ; multiplier = multiplier << 1, C = sign bit
BCR MULSEI ; if (sign bit was 1) {
SUB R3,R0,R5 ; product = product - multiplicand
MULSEI: ; }
LIS R6,31 ; i = 31
MULSLP: ; do {
SL R3,1 ; product = product << 1
SL R4,1 ; multiplier = multiplier << 1; C = top bit
BCR MULSEIL ; if (top bit was 1) {
ADD R3,R3,R5 ; product = product + multiplicand;
MULSEIL: ; }
ADDSI R6,-1 ; i = i - 1
BGT MULLP ; } while (i > 0)
JUMPS R1 ; return
|
The above code is pleasantly compact, but it can be accelerated by all of the methods we have already discussed. For example, the loop may be partially unrolled to reduce the number of iterations or completely unrolled in order to eliminate the loop counter. Consider, for example, using a 3-way unrolling, where the loop would iterate 10 times with 3 multiply steps in the loop body, and then one more multiply step outside the loop body before the final step that subtracts the multiplicand if the multiplier is negative.
l) Write Hawk code for a naieve signed multiply routine that calls the unsigned multiply routine given previously.
m) Write C, C++ or Java code for a naieve signed divide routine that calls something akin to the unsigned divide routine given previously.
n) Modify the code for the signed multiply routine given here so that it computes the 64-bit product in registers 3 and 4. Note that this is almost an easy job: all you need to do is replace the two independent shifts of registers 3 and 4 with a single 64-bit shift.
o) Modify the code for the signed multiply routine given here to use 15 iterations where each iteration includes an unrolling of the loop.
p) Modify the code for signed multiply given here to do unsigned multiplication, and then compare it with the unsigned multiply code given previously. Which would be faster, and why?
As already noted, the Hawk architecture includes support for long shifts composed of a number of shorter 32-bit shifts. The same special support instructions that permit this are also useful for high precision addition and subtraction. Thus, if some problem requires the use of 128-bit numbers, for example, using registers 4 to 7 to hold one number and registers 8 to 11 to hold another, we can add or subtract these two numbers as follows:
ADD R4,R4,R8 ; add least significant 32 bits first
ADDC R5,R9 ;
ADDC R6,R10 ;
ADDC R7,R11 ; add most significant 32 bits last
|
SUB R4,R4,R8 ; subtract least significant 32 bits first
SUBB R5,R9 ;
SUBB R6,R10 ;
SUBB R7,R11 ; subtract most significant 32 bits last
|
There are two ways to build a high-precision multiply routine. One is to simply take a simple binary multiply routine and expand it, using multi-register shifts and multi-register adds. The other is to build a high-precision routine from multiple applications of a low precision routine. Given a 32-bit unsigned multiply, where ab and cd are 64-bit quantities, with a and c being the most significant half of each and b and d the least significant half, the product ab×cd is a×c×264+a×d×232+b×c×232+b×d.
Note that shifts by multiples of 32 bits, equivlent to multiplication by powers of 232, are done trivially by moving or adding to the appropriate higher-numbered register in the array of registers holding the multiple-precision result. As a result, we can use 32-bit multiplies that produce 64-bit products, and only use long add sequences for the final sum. This extended precision multiply algorithm was thoroughly documented by Charles Babbage back in the 19th century, although he did it in decimal.
q) Write Hawk code for a 128-bit right shift.
r) Write Hawk code for a 128-bit left shift.
s) Write Hawk code for a 64 bit unsigned integer multiply, producing a 128-bit product. There are two obvious ways to do this, one using long shifts and adds for each of the 64 iterations, and one using 4 calls to a 32-bit add routine.
While binary arithmetic is easy, it is not the only alternative. Most computers built in the 1940s and 1950s used decimal, and decimal remains common today because some programming languages, notably COBOL, require it. True, COBOL is an archaic language, but millions of lines of code written in COBOL remain at the heart of the corporate management information systems of most of the major corporations in the United States, so efficient support for this language cannot be ignored. In addition, many lab instruments use decimal because their primary output is to a decimal display, and when these instruments have computer interfaces, the data is usually sent out in decimal. The internal number representations used on most pocket calculators are also decimal.
How are decimal numbers manipulated on binary computers? There are two common schemes, binary coded decimal and excess three. Both use 4 bits per decimal digit, but the coding systems differ:
| BCD | decimal | Excess 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0 | 0011 | ||||||||
| 0001 | 1 | 0100 | ||||||||
| 0010 | 2 | 0101 | ||||||||
| 0011 | 3 | 0110 | ||||||||
| 0100 | 4 | 0111 | ||||||||
| 0101 | 5 | 1000 | ||||||||
| 0110 | 6 | 1001 | ||||||||
| 0111 | 7 | 1010 | ||||||||
| 1000 | 8 | 1011 | ||||||||
| 1001 | 9 | 1100 | ||||||||
Binary coded decimal or BCD uses the natural binary representation for each decimal digit, while excess 3 adds three to the simple binary value of each digit. The reason this is useful will become clearer in a moment, but one benefit of this is that the excess three system is symmetric in the sense that the numbers 5 and above are represented by the one's complements of the numbers below 5. This makes 10's complement representations of signed numbers work nicely, if it is assumed that values of the most significant decimal digit of 5 or greater represent negative numbers.
The hard part of designing a decimal adder is figuring out when to
generate a carry out of each decimal digit position. We do this
when sum of two digits is greater than 10. We
could construct a decimal adder directly, with circuitry to compare
digits of the sum with 10, but there is a simpler way.
The trick, known since the 1950s, is to bias the numbers so
that the simple binary carry out of each digit position is right.
We do this by adding 6 to each BCD digit of the sum, or alternately,
by using an excess-3 representation where an extra 3 is included in
each digit. Of course, after
this is done, corrections must be made to the result.
Here is an example addition problem, done with 8-bit 2-digit BCD numbers:
| 1 | 1 | 1 | carry bits | |||||||
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | addend = 45 | ||
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | augend = 46 | ||
| + | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | sixes | |
| | ||||||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | preliminary sum | ||
| – | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | correction | |
| | ||||||||||
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | the sum = 91 | ||
Here the initial sum for the decimal digits that produced a carry is correct, but the sum for digits that did not produce a carry is off by 6. To fix this, we subtract 6 from the digits that did not produce a carry. With the excess-three representation, the required correction is only slightly different: We subtract 3 from the digits that did not produce a carry and add three to the digits that did.
The BCD carry field in the processor status word of the Hawk records the carry out of each decimal digit after each add instruction. The idea is borrowed from the Intel 8080. The only use for this field is to support BCD and excess-3 arithmetic.
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 00 |
| BCD carry | N | Z | V | C | |||||||||||||||||||||||||||
The BCD-carry field is used by the ADJUST instruction to perform the appropriate adjustment after the preliminary ADD instruction to complete the BCD or excess-3 sum, as illustrated here:
; assumption: R3 and R4 contain BCD numbers LIW R5,#66666666 ADD R5,R5,R3 ; correct addend by sixes ADD R5,R5,R4 ; produce preliminary sum ADJUST R5,BCD ; correct the result using the BCD carry bits ; result: R5 = R3 + R4, the BCD sum |
; assumption: R3 and R4 contain excess-3 numbers ADD R5,R3,R4 ; produce preliminary sum ADJUST R5,EX3 ; correct the result using the BCD carry bits ; result: R5 = R3 + R4, the excess-3 sum |
Here, the advantage of excess-3 should be clear: With BCD, we must keep the constant 6666666616 in a register, and we must always add this constant to one of our operands before each addition. With excess 3, because the extra 6 is incorporated into the values before addition, all we need to do is make a slightly more complex correction after each sum.
t) Write Hawk code to take the 10's complement of a BCD number and then explain how to detect if the result is positive or negative.
u) Write Hawk code to take the 10's complement of an excess-3 number and then explain how to detect if the result is positive or negative.
v) Write Hawk code to convert from excess 3 to BCD and from BCD to excess 3.
w) What value is added to or subtracted from each decimal digit by the ADJUST ...,EX3 instruction? You may have to work a few examples to figure this out.
Floating point arithmetic is a common feature of modern computers, but at the start of the computer age, it was not obvious that there was any need for it. John Von Neumann is reputed to have said "a good programmer should be able to keep the point in his head," when someone asked him about the value of floating point hardware. How do you keep the point in your head? The answer is remarkably easy. You do arithmetic using integers, but instead of counting, say, integer numbers of inches, you count integer numbers of fractional inches. If you are working in base 10, you might work in hundredths of an inch. If you are working in binary, you might use 128ths of an inch.
32-bit binary numbers represented as integer counts of 128ths of an inch can be thought of as follows:
| 24 | 23 | 22 | 21 | 20 | 19 | 18 | 14 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 00 | -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| Integer part | Fraction | ||||||||||||||||||||||||||||||
The bits of the fixed point fraction given above have been renumbered, so instead of considering the most significant bit to be bit 31, it is bit 24, and instead of considering the least significant bit to be bit 0, it is bit –7. This is because the least significant bit has the weight 2–7 in the place-value system, or 1/128, and the most significant bit has the value 224. It is useful to number the bits so that the one's place is numbered 0. When we write a number on paper, this is exactly what the point signifies. That is why we avoid the use of the term decimal point here, because the point does not in any way depend on the number base — in any number base, however, it marks the one's place, or the dividing line between the integer part of the number and the fractional part.
Consider the binary number 0.1000000; this is 1/2 or 64/128. Similarly, 0.0100000 is 1/4 or 32/128 in the fixed point number system outlined above. If we want to represent 0.110, we cannot do it exactly in this system; the closest we can come are 0.0001100, which is 12/128 or 0.9375, on the low side, and 0.0001101, which is 13/128 or 0.1015625, on the high side. The fundamental problem we face is that there is no exact representation of one tenth in binary, just as there is no exact representation of 1/3 in decimal. All we can hope for is a good approximation.
The rules for dealing with binary fixed point arithmetic are exactly the familiar rules for dealing with decimal fractions. When adding or subtracting two fixed-point numbers, first shift them to align the points, and then add or subtract. When multiplying, first multiply and then count off the digits left of the point on the multiplier and multiplicand and then count off the sum of these to determine where the point goes in the product.
A C programmer using the fixed point number represeentation here would do arithmetic as follows:
int a, b, c; /* fixed point, 7 places right of the point */ int d; /* fixed point, 14 places right of the point */ /* all variables have the point in the same place, easy? */ a = b + c; /* no shifts needed */ a = b - c; /* no shifts needed */ a = (b * c) >> 7; /* product had 14 places left of the point */ /* variables with point in different places */ d = (a + b) << 7; /* shift result to fit */ a = (d >> 7) - b; /* align points before subtract */ d = b * c; /* luck! product has right number of places */ |
Unfortunately, languages like C and Java provide no help to the programmer when doing fixed point arithmetic. Thus, it is up to the programmer to remember to shift all constants appropriately, or to code them with the correct built-in bias, and it is up to the programmer to remember to shift operands left or right as needed. This is something that John Von Neumann thought programmers could do in their heads, but it was clear by the early 1960's that programmers had real difficulty doing this. Floating point hardware or software eliminates the need for this.
x) Given that the divisor and the dividend have points in the same place, where is the point in the quotient? Where is the point in the remainder? For a concrete example, consider the possibility that both divisor and dividend have 7 places after the point.
y) Give Hawk code to split a 2's complement fixed-point number given in register 3 into its integer part, in register 3, and its fractional part, in register 4. The initial number should have 7 places after the point. The fractional part of the result will have one bit for the sign and 31 bits after the point.