A Problem: Give the logic diagram (in graphical notation) for the logic that produces a true output if the BGT instruciton is supposed to branch, and a false output if not. (0.5 points)
The Hawk manual documents BGT as branching if (N⊕V)∧~Z. The C condition code is ignored. This leads to:
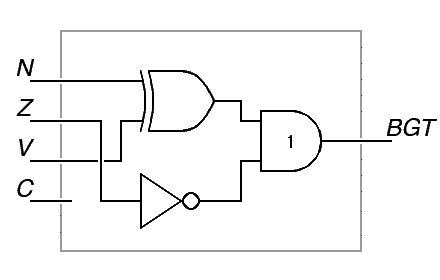
Of course, drawing in the C condition code is not necessary, nor is it necessary to draw the N, Z and V condition codes in any particular order. If someone drew out the full sum-of-products (or other equivalent) diagram for the exclusive-or gate, that would be wasted effort but not wrong.
leftshift( int a, int c) { // iterative shifter
while (c > 0) { a = a << 1; c = c - 1; }
return a;
}
Consider the following alternative:
leftshift( int a, int c) { // software barrel shifter
if (c & 1) a = a << 1;
if (c & 2) a = a << 2;
if (c & 4) a = a << 4;
if (c & 8) a = a << 8;
if (c & 16) a = a << 16;
return a;
}
The iterative shifter and the barrel shifter produce the same result for all values of c from 1 to 31.
a) What is the result of the iterative shifter for larger values of c? (0.2 points)
zero for all larger values of the shift count.
b) What is the result of the barrel shifter for larger values of c? (0.2 points)
a << (c & 31) which is the same as a << (c % 32) for all values of the shift count.
That is, it only uses the low 5 bits of the count, ignoring all higher bits.
c) Code the barrel shifter as a SMAL Hawk assembly language subroutine. Take advantage of the BITTST instruction for testing individual bits of a register (see Section 6.4 of the Hawk manual). (0.6 points)
LEFTSHIFT: ; given R3 = a, the value to be shifted
; R3 = c, the shift count
BITTST R4,0
BBR LSNO0 ; if (c & 1) {
SL R3,1 ; a = a << 1
LSNO0: ; }
BITTST R4,1
BBR LSNO1 ; if (c & 2) {
SL R3,2 ; a = a << 2
LSNO1: ; }
BITTST R4,2
BBR LSNO2 ; if (c & 4) {
SL R3,4 ; a = a << 4
LSNO2: ; }
BITTST R4,3
BBR LSNO3 ; if (c & 8) {
SL R3,8 ; a = a << 8
LSNO3: ; }
BITTST R4,4
BBR LSNO4 ; if (c & 16) {
SL R3,16 ; a = a << 16
LSNO4: ; }
JUMPS R1 ; return a
a) × 120. (0.3 points)
Note that 120 = 2 × 3 × 4 × 5 = 3 × 5 × 8. This leads to:
ADDSL R3,R3,1 ; -- times 3 ADDSL R3,R3,2 ; -- times 5 SL R3,3 ; -- times 8The above three lines of code can, of course, appear in any order because multiplication is commutative. This applies to the following as well.
b) × 192. (0.3 points)
Note that 192 = 3 × 64. This leads to:
ADDSL R3,R3,1 ; -- times 3 SL R3,6 ; -- times 64
c) × 500. (0.3 points)
Note that 500 = 5 × 5 × 5 × 4
ADDSL R3,R3,2 ; -- times 5 ADDSL R3,R3,2 ; -- times 5 ADDSL R3,R3,2 ; -- times 5 SL R3,2 ; -- times 4
Hint: Two 4-bit right-shift instructions get all but 4 bits of the result correct. The problem is to rescue those 4 bits. This can be done with some left shifting and an add. Keep in mind that the maximum shift count that the hawk permits is 16, but some of the shifting you need to do requires more. This will take multiple instructions. and an add
There are many solutions that are equivalent:
MOVESL R1,R4,14 ; \ rescue and align 4 bits of R4 SL R1,14 ; / SRU R3,4 SRU R4,4 ADD R3,R3,R1 ; put the rescued bits into R3Recall that the shift count on all shift instructions is limited to 16. All that matters is that the two left shifts above combine to make a 28 bit shift, moving the lost 4 bits into position to put in place. The two right shifts can be in any order, and R3 can be shifted before rescusing the low bits of R4. Also, an OR instruction can be used instead of ADD, and this can be placed any time after R3 is shifted.