Assignment 7, due Oct 17

S:      ; given:   R3 = s1, pointer to null-terminated string 1
        ;          R4 = s2, pointer to null-terminated string 2
        ; returns: R3 = result of comparing strings 1 and 2
        LOADS   R5,R3
        EXTB    R5,R5,R3
        LOADS   R6,R4
        EXTB    R6,R6,R4
        BZS     Q
        CMP     R5,R6
        BNE     Q
        ADDSI   R3,1
        ADDSI   R4,1
        BR      S
Q:      SUB     R3,R5,R6
        JUMPS   R1

a) For strings s1 and s2 of equal length, what return value (or range of values) indicates that s1 comes before s2 in alphabetical order? (0.2 points)

If s1 comes before s2, R3 < 0; note that because we are comparing two one-byte values, the value is never less than –255.

b) For strings s1 and s2 of equal length, what return value (or range of values) indicates that s1 is the same as s2? in alphabetical order. (0.2 points)

If s1 and s2 are identical, R3 = 0.

c) For strings s1 and s2 of equal length, what return value (or range of values) indicates that s1 comes after s2 in alphabetical order? (0.2 points)

If s1 comes after s2, R3 > 0; note that because we are comparing two one-byte values, the value is never greater than +255.

d) For strings s1 and s2 of different lengths where the text of the strings is the same up to the end of the shortest, what return value (or range of values) indicates that s1 is longer than s2. (0.2 points)

If s1 is longer than s2 which is its prefix, R3 > 0;

e) For strings s1 and s2 of different lengths where the text of the strings is the same up to the end of the shortest, what return value (or range of values) indicates that s1 is shorter than s2.

If s1 is shorter than and a prefix of s2 R3 < 0;

a) Give the algebraic sum of products representation of this function, using a notation comparable to f(x,y)=xy+y (0.5 points)

f(a,b,c) = a b c + a b c + a b c + a b c

b) Draw the logic circuit for this function, using the notion of an and-array and an or-array described in Chapter 8 of the notes. Neatness counts! (0.5 points)

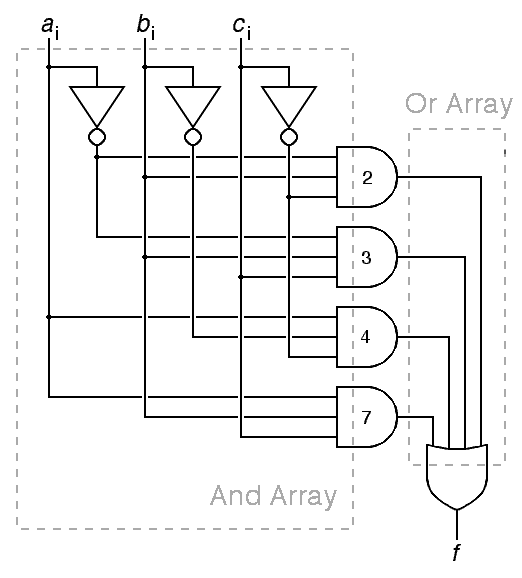
Note that a student solution that decoded all 8 terms in the and array and then ignored half of them would be acceptable.

Assignment: Make a truth table for the modified adder with 8 rows selected by inputs a_i, b_i and c_i, and with 4 different groups of output columns. Each group of output columns should give c_i+1 and s_i for one of the combinations of f₁, f₂ and f₃ that are mentioned in the notes. (1.0 points)

Note: For reference, here are the 4 combinations that the notes discuss. You may use the labels normal, xor, or and and to label your column groups.

f1   f2   f3   use  1 1 0 normal 1 0 0 xor 1 0 1 or 0 0 1 and

The problem is solved here:

ai	bi	ci	normal		xor		or		and
			ci+1	si	ci+1	si	ci+1	si	ci+1	si
0	0	0	0	0	0	0	0	0	0	0
0	0	1	0	1	0	1	0	1	0	1
0	1	0	0	1	0	1	0	1	0	0
0	1	1	1	0	1	0	1	0	1	0
1	0	0	0	1	0	1	0	1	0	0
1	0	1	1	0	1	0	1	0	1	0
1	1	0	1	0	0	0	0	1	0	1
1	1	1	1	1	1	1	1	1	1	1

In the above, note that the output for c_i+1 is frequently nonzero, but for the logic operations, this only occurs when c_i is nonzero, and for logic operations, we are guaranteed that this will never be the case.