SUBTITLE "REVERSE - reverse the order of bytes in a word"
; when called, it reverses the byte order of the word
; activation record structure
;RETAD = 0
REVERSE: ; expects R3 = pointer to a word in RAM
; conforms to the usual Hawk caling sequence
; when called, reverses the byte order of the word
JUMPS R1
If REVERSE is called to operate on a word containing 0123456716, the word will be changed to hold 6745230116; that is, the order of the bytes in the word will be reversed.
The problem: Flesh out the subroutine so it works as specified. It's all a matter of extracting and stuffing the bytes. (1 point)
There are many possible solutions. Here is one that is obvious, using a for loop to get successive bytes from one register and stuff them into another.
SUBTITLE "REVERSE - reverse the order of bytes in a word" ; when called, it reverses the byte order of the word ; activation record structure ;RETAD = 0 REVERSE: ; expects R3 = (src) pointer to a word in RAM ; conforms to the usual Hawk caling sequence ; when called, reverses the byte order of the word LEA R4,R3,3 ; dst = src+3 -- pointer to last byte LIS R5,4 ; count = 4 LOADS R6,R3 ; srcbuf = word from RAM REVLP: ; do { EXTB R1,R6,R3 ; temp = srcbuf[src] STUFFB R7,R1,R4 ; dstbuf[dst] = temp ADDSI R3,1 ; src++ ADDSI R4,-1 ; dst-- ADDSI R5,-1 ; count-- BGT REVLP ; } while (count > 0) STORES R7,R3 ; word in RAM = dstbuf JUMPS R1Here is a completely different solution that is much faster. It has no loop and it uses shift operations. There is an even faster solution that is a hybrid of the one above with this one:
SUBTITLE "REVERSE - reverse the order of bytes in a word" ; when called, it reverses the byte order of the word ; activation record structure ;RETAD = 0 REVERSE: ; expects R3 = (src) pointer to a word in RAM ; conforms to the usual Hawk caling sequence ; when called, reverses the byte order of the word LOADS R4,R3 ; srcbuf = word from RAM MOVE R5,R4 TRUNC R5,8 ; dstbuf = srcbuf & 0xFF SR R4,8 ; srcbuf = srcbuf >> 8 SL R5,8 ; dstbuf = dstbuf << 8 MOVE R6,R4 TRUNC R6,8 OR R5,R6 ; dstbuf = dstbuf && (srcbuf & 0xFF) SR R4,8 ; srcbuf = srcbuf >> 8 SL R5,8 ; dstbuf = dstbuf << 8 MOVE R6,R4 TRUNC R6,8 OR R5,R6 ; dstbuf = dstbuf && (srcbuf & 0xFF) SR R4,8 ; srcbuf = srcbuf >> 8 SL R5,8 ; dstbuf = dstbuf << 8 MOVE R6,R4 TRUNC R6,8 OR R5,R6 ; dstbuf = dstbuf && (srcbuf & 0xFF) STORES R5,R3 ; word in RAM = dstbuf JUMPS R1
a) Give the truth table for this alternative way to compute the V condition code. (0.5 point)
a b s || v -------++--- 0 0 0 || 0 0 0 1 || 1 0 1 0 || 0 0 1 1 || 0 1 0 0 || 0 1 0 1 || 0 1 1 0 || 1 1 1 1 || 0
b) Draw a schematic diagram for hardware to compute this function, using only and, or and not gates. (0.5 point)
In textual form, the answer could be stated as:
v = ((not a) and (not b) and s) or (a and b and (not s))The diagram that follows is done with the logic gates arranged into an and array and an or array, following the standard derivation from the truth table given above.
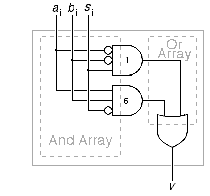
An alternative approach to making an ALU do logic operations is to add extra inputs to the adder. Each of these extra inputs goes to one or more of the and gates in the and array of the adder. If all these extra inputs are one, the and array is fully enabled and the adder just adds. Setting each of these extra inputs to zero disables some subset of the and gates in the and array, forcing the adder to do some logic function.
a) Which gates in the and array of the adder should you disable to make the adder perform an exclusive-or operation? Hint: add becomes exclusive-or if you make it ignore the carry in line. (0.3 point)
If we assume that carry in will always be zero for logic operations, this already disables rows 1, 3, 5 and 7. We need to guarantee that carry out will be zero in order to guarantee this for the next stage of the ALU, so we disable row 6, and optionally also 1, 3, 5 and 7. We leave rows 2 and 4 active.
b) Which gates in the and array of the adder should you disable to make the adder perform just an or operation? (0.3 point)
We need to disable everything that was disabled in part a), but as discussed in class, completing the or function requires adding a row that is a duplicate of row 6 but is connected to the sum output and is enabled for or, and disabled for exclusive or. It is not part of the assignment, but worth noting that this added gate also lets us compute the and function if we enable it and disable rows 2 and 4.
c) Draw the gate-level schematic view of an addre augmented with the auxiliary inputs supporting your answers to parts a and b. (0.4 point)
The following diagram incorporates all of the components from parts a and b, including the extra gate in row 6 and the extra control input (not part of the assignment) needed to compute just the and function.
