11. Simple Input and Output.
Part of
22C:40, Computer Organization and Hardware Notes
|
Up to this point, we have relied on the Hawk monitor to provice input-output services. Now, it is time to descend into the system and look at the actual input-output interface of our hardware. In the case of the Hawk architecture, the keyboard and display are examples of two entirely distinct classes of input-output devices. The Hawk keyboard interface is a byte sequential or serial interface, able to receive one byte at a time from the keyboard, where each byte represents a single character. In contract, the display is a memory-mapped output device, which is to say, the display hardware constantly updates the display screen from a region of memory called the video RAM because classic display screens used video technology.
Historically, there have been several major approaches to device access. In the earliest computers, those designed from the 1940s into the early 1960s, each device was supported directly by its own instructions, so the central processor would interpret instructions such as start punched-card read cycle or set magnetic drum track number. By the 1960s, it was clear that most input-output instructions involved either setting, testing or reading the values of device control registers, so instead of using distinct opcodes for each device operation, computers were designed with a small set of instructions for operating on device registers, with a field of the instruction used to select the device register.
The Digital Equipment PDP-5 computer was a typical member of this class. This machine had a single instruction called IOT or input-output transfer that included a 6-bit field for selecting the device and a 3-bit field that was passed to the device indicating, to the device, the operation being requested. Typical devices supported at least 3 operations, clear flag bit, skip if flag bit set, and read (for input devices) or write (for output devices). The read and write operations moved data between the device data register and a register inside the processor.
On computers designed after the 1950s, it has been common to access devices using an input-output bus. Physically, an input-output bus is a set of wires that connect, physically, to all of the devices. The term bus itself dates back to the early days of electric generating stations. A bus is an electrical conductor, or a group of conductors that are used to send power, or later, signals, from anywhere to anywhere. The term is short for omnibus, a term that implies this anywhere to anywhere character. In generating stations, each generator is connected to the main bus for the power plant, and all of the outgoing transmission lines are also connected to that bus. The bus can therefore deliver power from any generator to any power line.
The input-output bus of a computer system carries signals that select a particular device, the device address, and that are used to transfer data to or from a device. Similarly, the main memory bus of a computer carries signals that select a particular memory location, the memory address, and that are used to transfer data to or from that location. This parallel was first exploited in 1970, when Digital Equipment Corporation came out with the PDP-11 computer. In this computer, there was only one bus, the Unibus, and the special registers of each device were simply addressed as if they were memory locations. This is the approach we take on the Hawk, where addresses above FF00000016 are interpreted as references to input-output device registers instead of locations in memory.
The Hawk keyboard interface is considerably simpler than the keyboard interface of a modern computer for two reasons. First, many modern computers use the universal serial bus (USB) standard for access to devices like the keyboard. This standard is really a computer network standard, and for practical purposes, each device connected to this bus must have a small processor in the device to manage the communication protocols of the device.
The second factor that complicates the keyboards of many modern computers is the fact that they are excessively programmable. The need to reprogram the keyboard is fairly obvious. A keyboard manufacturer typically wants to sell the same keyboard hardware with different keycaps for every language in the world, so reprogramming the keyboard to support different languages is quite natural. This problem is equally easy to solve in software within the operating system, but the system software of the personal computers that dominated the 1980s was so bad that standard keyboards emerged that supported hardware solutions to what should probably have been a software problem.
Our simplified keyboard interface contains just two registers, a keyboard status and control register and a keyboard data register. The keyboard data register, at memory address FF10000016 contains one byte holding the most recent character typed on the keyboard. The keyboard status and control register, at address FF10000416 also looks like a one byte register, but in fact, it only has 3 bits that are defined, one to report that a key has been pressed, one to report errors, and one to control whether keypresses cause interrupts, a subject we will discuss in the next chapter.
| FF100000 |
| Keyboard data register | ||||||||||||||||
| FF100004 |
| Keyboard status and control register | ||||||||||||||||
| IE = interrupt enable (control) | ||||||||||||||||||
| ER = error (status) | ||||||||||||||||||
| RD = input data ready (status) | ||||||||||||||||||
The most fundamental piece of status information offered by most devices is a single bit, ready. This bit is set, by the device, whenever it is time for the software to transfer more data to or from the device, and it is typically reset automatically as a side-effect of the actual data transfer. In the case of the keyboard interface given here, the ready bit is set whenever someone presses a key on the keyboard, and it is reset by reading the value of the keyboard data register.
A second status bit commonly found in many devices is used to report errors. In the case of our simple keyboard, there is really only one error that is worth reporting, and that is the overrun error, an event that occurs if a user hits a second key on the keyboard before the software has had time to read the first. The hardware can detect an overrun error easily. This occurs if a key is pressed while the ready bit is already true. For our interface, this bit is reset whenever the ready bit is reset.
The only control bit in our keyboard interface is the interrupt enable bit. This bit is set and reset by software. If this bit is reset, the keyboard interface cannot request an interrupt. If this bit is set, the keyboard interface will request an interrupt whenever the keyboard ready bit is true. Interrupts are discussed in the next chapter, but here, it is worth pointing out that most devices on modern computers are able to request an interrupt.
We now have enough information to write some simple application software that reads from the keyboard. Whenever the application program wants to await a keypress, it can check the keyboard data ready bit, and as soon as this bit becomes one, the software can read the ASCII code corresponding to the key that was pressed from the keyboard data register. Here is the code:
TITLE kbdread.a -- read from the keyboard
USE "hawk.macs"
; keyboard interface description
PKBD: W #FF100000 ; address of keyboard interface
KBDDATA = 0 ; offset of keyboard data register
KBDSTAT = 0 ; offset of keyboard status register
; bits in keyboard status register
KSTATRD = 0 ; ready
KSTATER = 6 ; error
KSTATIE = 7 ; interrupt enable
INT KBDGET
KBDGET: ; link through R1
; returns R3 = keyboard
; uses R4
LOAD R4,PKBD ; R4 = pointer to keyboard interface
KPDPOLL: ; do {
LOAD R3,R4,KBDSTAT
BITTST R3,KSTATRD
BCR KBDPOLL ; } while ((kbdstat & kstatrd) == 0);
LOAD R3,R4,KBDDATA
JUMPS R1 ; return kbddata;
|
The loop in the above code is called a polling loop. The word polling here has the same root as in the phrase going to the polls meaning to vote or in the phrase a public opinion poll. In general, the verb to poll means to ask a question. Our polling loop asks one question over and over: Has anyone hit a key on the keyboard yet? In general, polling loops perform poorly, particularly short polling loops of the sort illustrated here. Nonetheless, this approach is quite common for simple low performance input-output operations on small computers.
Exercises
a) The KBDGET routine shown here acts silently, without echoing what you type on the display. Write a routine called KBDECHO that gets one character from the keyboard and echoes it to the display (using DSPCH from the Hawk monitor), but only echoes printable characters, not nonprinting characters.
b) In code for a low-end system, the most common response to an input error is to ignore it. Suggest an appropriate response for a high-end system, for example, for a word-processor intended for use by professional typists who routinely type without looking at the screen (because they are looking at the text they are transcribing).
c) A typical fast typist can type 60 words per minute, where a word is 5 letters, on the average, and most words are separated by spaces. How frequently should the ready bit be polled to keep up with such a typist? If the CPU can execute 1,000,000 instructins per second (a typical number for 1975), how many times a second will the KBDGET routine poll the ready bit, while waiting for input? Does this suggest an imbalance?
The strange structure and behavior of the keyboard status register should raise some questions: How can a register be built with missing bits in the middle of it? How can a register be built where some bits change from zero to one when someone hits a key on the keyboard, and then change from one to zero when a program reads data from some other register? To understand the answer to these questions, it is helpful to take a look at the gate level implementation of registers. The discussion here actually applies to all registers, including the registers in the central processor, but we will focus our illustrations here on one problem, the implementaton of the keyboard status and control register.
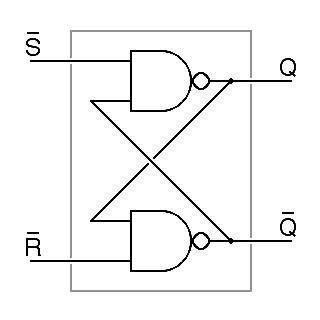
The fundamental component used to store one bit of information inside a computer is the flipflop, known more formally as the bistable multivibrator. Hardly anyone uses the latter term, but it is the original name of this circuit, dating to 1919, when Eccles and Jordan developed a family of multivibrator circuits using vacuum tubes, one of which had two stable states and could be made to flip between them. By 1946, the term flipflop was already common. It was the discovery of this circuit that led, first, to the development of very high-speed counter circuits built from vacuum-tubes, and then to the development of more complex digital logic. At the logic level, a flipflop can be constructed from two nand gates, as shown here:

| 
|
| Q = S nand Q | |
| Q = R nand Q | |
The names Q and Q are conventionally used for the outputs of all flipflops. This is something of an abuse in this case, because if R and S are both zero, both Q and Q will be one, despite the conventional reading that Q means not Q. We get around this by simply declaraing that we never want to allow R and S to be zero at the same time. Given this assumption, it turns out that Q and Q will always settle down to opposing values.
Note that in the abbreviated schematic symbol for this flipflop, given on the right in the figure, the inputs are labeled as R and S instead of R and S, with the inversion shown using bubbles on each input. The outputs are still called Q and Q. This is a matter of deeply entrenched tradition more than of necessary usage.
One way of thinking about this flipflop circuit is to focus on its description as a set of Boolean equations. We have two equations in two unknowns, and just as in conventional algebra, this means we may have two solutions. If R and S are both one, there are two different solutions, where for each of the other possible inputs, there is a unique solution to this system of equations, as summarized in the following truth table:
| R | S | Q | Q | description | ||
| 0 | 0 | 1 | 1 | forbidden | ||
| 0 | 1 | 0 | 1 | reset | ||
| 1 | 0 | 1 | 0 | set | ||
| 1 | 1 | 0 | 1 | hold | ||
| 1 | 0 | |||||
Normally, an R and S flipflop is maintained in the hold state, with both inputs set to one. In this state, the flipflop holds the value stored in it indefinitely. If R is goes to zero, the Q output goes immediately to zero, and it stays zero after R returns to one; this is why R is referred to as the reset input. Similarly, bringing S to zero sets Q to one, so S is referred to as the set input. The fact that these inputs are marked with inverter bubbles in the shorthand notation and with overbars in the longhand notation is because these inputs are normally one and the set and reset actions occur when they go to zero. The behavior of this flipflop is described by a timing diagram, in which the inputs and outputs of the flipflop are plotted as a function of time:

|
In the above timing diagram, the initial state of the flipflop is unknown, so both outputs are shown as being simultaneously zero and one. No physical implementation of a logic gate will operate instantaneously, so the outputs are shown changing with a slight delay after each input change. The first negative pulse on S, arriving at time 1, sets Q to one and Q to zero. The next pulse, at time 2, is a negative pulse on R that sets Q to zero and Q to one. The simultaneous pulses on R and S at time 3 cause trouble. During these pulses, both outputs are one, but when the inputs go back to zero, the behavior of the flipflop becomes unpredictable. Eventually, it will settle into one of its two stable states, but we cannot predict which state this will be, so our timing diagram shows both zero and one until the flipflop is set into a well determined state by the pulse at time 4.
This basic flipflop and its close cousin, the RS flipflop, are found at the heart of every memory technology from static RAM to the bits of the registers in the central processor. RS flipflops differ from the RS flipflop only by the sign of the pulses on the inputs needed to set and reset the flipflop. The only forms of memory that are not, ultimately, based on such flipflops are the various dynamic memory technologies, ranging from the ancient Williams tube to modern DRAM and SDRAM chips. These dynamic technologies store each bit as charge on a capacitor, and this charge, once stored, leaks slowly away. This is why they are called dynamic technologies. The only reason that they function acceptably as memory is that some processor constantly scans the contents of memory and refreshes the data. While this has been done by the central processing units of some computers, the refresh function is usually carried out by a special purpose processor such as a memory controller; sometimes the refresh processor is integrated onto the memory chip itself.
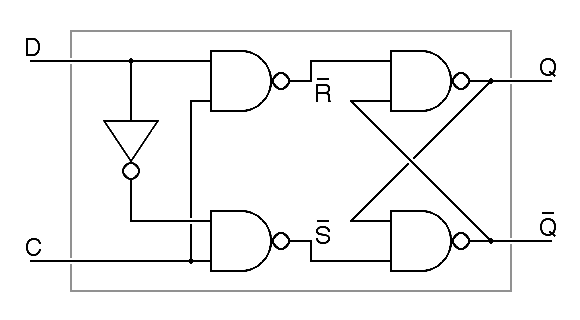
There are more complex forms of flipflops that we must examine before returning to our discussion of input-output interfaces; all of these are constructed from an R S flipflop augmented with additional gates. One problem with the basic R S flipflop is that we use two distinct inputs to store zero or one. If we want to build a memory, what we want is one input holding the value to be stored and another input that indicates when to store the data. Such a device is called a type-D latch, and it can be built from an R S flipflop with two additional nand gates and an inverter:
| 
|
| Q = (D nand C) nand Q | |
| Q = (D nand C) nand Q | |
The type-D latch operates as follows. When the C input is low, it forces the R and S inputs to the flipflop high, allowing the flipflop to remember a stored value. When the C input is high, the data from the D input forces one or the other of the R and S inputs low, setting the flipflop so that the Q output is equal to the D input. The inputs are named D for data and C for clock. The word clock is used because this input is frequently connected to a source of periodic pulses. The term latch is an anachronism, a reference to an older technology, the latching relay.
In the schematic abbreviation for the D latch shown on the right in the figure, note that the inputs are shown without any inversion. This is becuse the Q output follows the D input, without inversion, and because the C input is normally low when the flipflop is holding data, and is pulsed to high when a new value should be recorded. The basic D latch is not free of difficulty, as is illustrated in the following timing diagram.
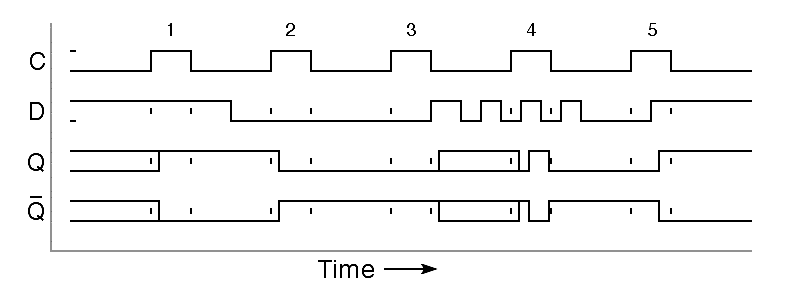
|
Notice here that the type-D latch is very well behaved when the D input does not change during pulses on the C input. In this case, the Q and Q outputs change shortly after the rising edge of the C input. This is illustrated by the behavior shown during clock pulses 1 and 2. Things are different if there are changes in the D input during the clock pulse. In the diagram above, the D input changes at the instant that clock pulse 3 ends, leaving the Q and Q outputs unpredictable. There is even the possibility that the flipflop may be left in an unstable state for a while before it settles in one of its two stable states.
After clock pulse 3 in the above timing diagram, the D input begins to behave very strangely. This has no effect on the output so long as the C input is low, but during clock pulse 4, this strange behavior passes through to the outputs. A single input change is shown during clock pulse 5; in this case, the outputs do not change at the start of the clock pulse, but instead shortly after the input change.
Many registers within computers are implemented using type-D latches. For example, the keyboard data register for the Hawk keyboard interface would most likely be built using 8 of these. Each time someone hits a key on the keyboard, the ASCII code for that key would be clocked into these latches.
Many computers of the 1950's and 1960's were built using no flipflop technology more advanced than the D-latch, but more complex flipflops are useful in some circumstances. With the advent of integrated circuits in the 1960's, a new family of flipflops came into widespread use. These are called master-slave flipflops because of how they are built, or edge-triggered flipflops because of how they behave.
A master-slave flipflop is built from two simple flipflops, a master and a slave, wired in series. The clock signal is distributed to these in such a way that only one of them is able to pass data at a time, so no matter what the value of the clock, so long as the clock input remains constant, no change to the data input is ever reflected in the output. Only when the clock input changes from zero to one does the output change. The following example is a negative edge triggered D flipflop built using the most obvious master-slave arrangement.
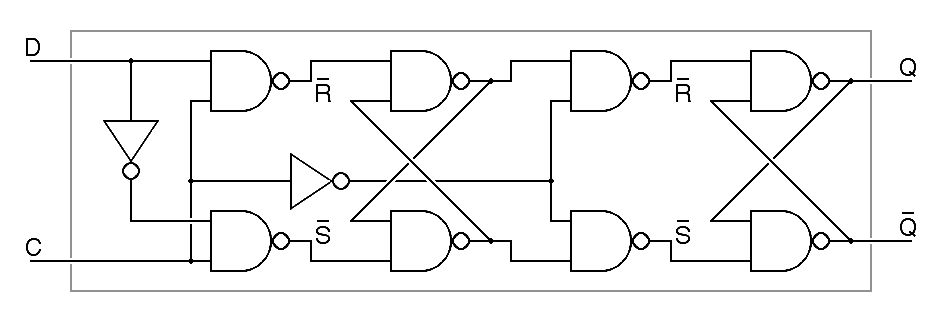
|
|
The master-slave design shown here has two RS flipflops, the master on the left and the slave on the right; when the clock input is low to the master, it is high to the slave, so the master holds the data and it is transmitted, unchanged, through the slave to the output. When the clock input is high to the master it is low to the slave, so the slave holds the output constant while the master attends to the data on the D input. Therefore, the output Q only changes on the high-to-low transition of the clock, so we say this is a negative-edge-triggered flipflop. In the abbreviated schematic notation, the triangle on the clock input indicates edge triggering, while the bubble negating the clock input indicates that the negative edge is the significant edge.
The timing diagram that follows has identical inputs as are shown in the timing diagram for the D latch, but because we are now using a negative-edge-triggered flipflop, the only time the output changes is when the clock input falls from one to zero. We are still faced with the possibility of an undetermined output if the data input changes at precisely the right moment near the time of the negative edge of the clock, but aside from this remote possibility, this flipflop comes close to the ideal we would hope for in a storage element.
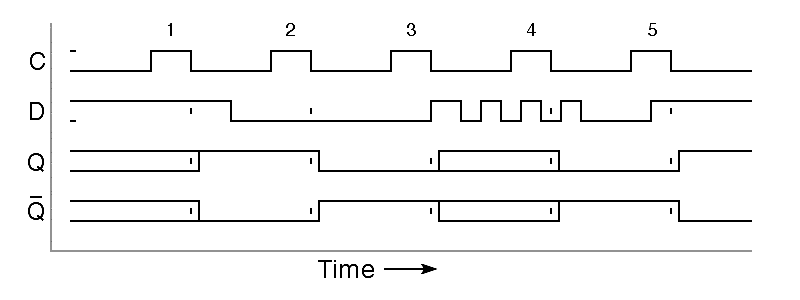
|
Commercial edge-triggered type-D flipflops were briefly made using designs close to that given here, but by 1970, optimized designs were common. Today's designs contain the equivalent of 6 nand gates with no inverters; these have about two gate delays from input to output, but they are difficult to understand compared to the simple design given here.
Exercises
d) Consider a circuit built using nor gates but wired identically to the RS flipflop shown here. Is the result a flipflop? If so, how is it set and reset? Is it equivalent to any flipflop discussed here?
e) Consider a circuit built with a type D latch where the Q output is fed back into the D input. What does this circuit do when the clock input is high?
f) Consider a circuit built with a negative-edge-triggered type D flipflop where the Q output is fed back into the D input. What does this circuit do each time the clock input changes from high to low?
g) How would you modify the design of the negative-edge-triggered type D flipflop shown here to make the flipflop trigger on the positive-edge of the clock pulse?
Given a supply of flipflops and a few other parts, we can build the Hawk keyboard interface. Here, we will assume a parallel keyboard that has 9 output wires. Of these, one keypress produces a positive pulse each time a key is pressed while The other 8 contain the binary code for the key that was pressed, but only when the keypress line is high.
We must also make some assumptions about the Hawk input-output bus interface. Here, we will assume that there is logic somewhere that decodes the memory address and delivers a positive pulse on the read FF100000 wire each time the CPU tries to read location FF100000, and similar logic for read FF100004 and write FF100004. We will also assume that the input-output data bus for the Hawk has wires labeled D7 through D0 carrying the least significant 8 bits of the input data during read operations and of the output data during write operations.
Given these assumptions, the keyboard data register for the Hawk can be constructed using 8 type-D latches, with the data input taken from the keyboard data lines and the clock inputs of all of the flipflops wired to the keypress line. The outputs of these flipflops must be connected to the Hawk input-output data bus when the read FF100000 line is high; this is done using special components called bus drivers, shown as triangles in the following diagram:
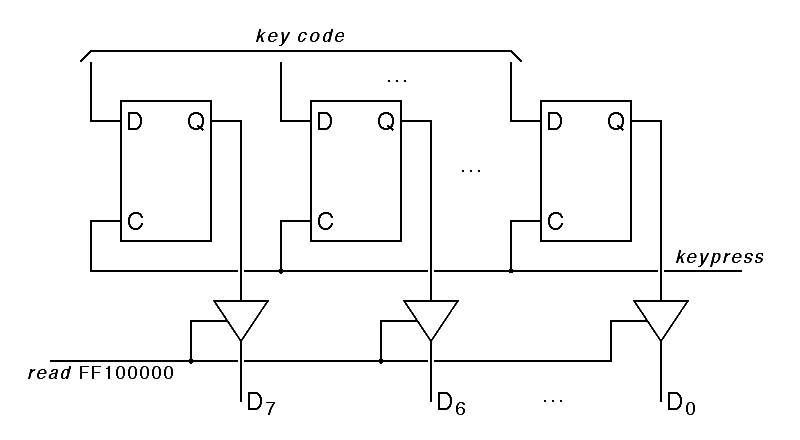
|
As mentioned in Chapter 8, a triangle with one input and one output is a a standard schematic symbol for an amplifier. The bus-driver symbol is based on this because bus drivers act as amplifiers when enabled, boosting the power enough to transmit a signal over a bus. When the bus driver is disabled, however, it is as if there were no bus connection at all. The enable signal is always shown entering the side of the triangle.
Here, we have used the convention that data flows down through the schematic diagram, while control signals enter from the sides, with the central processor on the left and the input-output device on the right. It is worth noting that if we build the the keyboard data register as shown here, it is a read-only register! No matter what a program running on the central processor does, the program cannot change the contents of the keyboard data register. The only way to enter data in this register is to press a key on the keyboard!
The keyboard status and control register is more complex, although it only involves three flipflops. The interrupt enable flipflop can be read and written by the central processor, while the other two have complex behavior, as shown below:
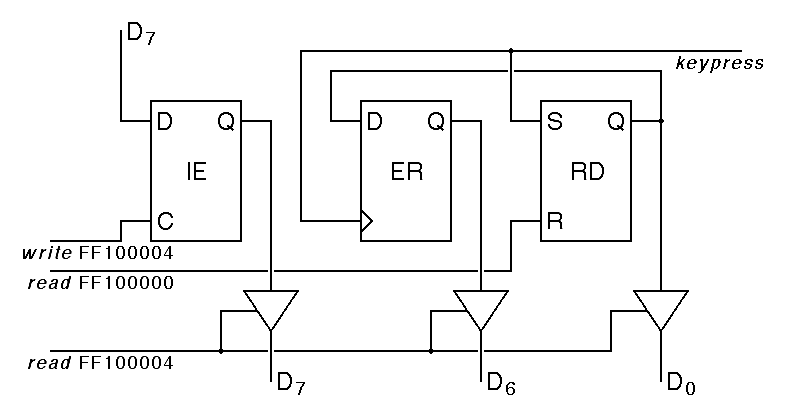
|
The keyboard ready flipflop, attached to D0, is perhaps the easiest to understand. This is a simple RS flipflop, set by a positive pulse on the keypress input, and reset by a positive pulse on the read FF100000 input, indicating a read from the keyboard data register. Note that an RS flipflop differs from the RS flipflops we have discussed in only one trivial way -- the flipflop is set and reset by positive pulses on the S and R inputs instead of by negative pulses on the S and R inputs. In schematic diagrams, this is signified by omitting the bubbles from the inputs to the flipflop.
The interrupt enable flipflop is also fairly easy to follow. This flipflop is a type-D latch, with data taken from D7 whenever there is a positive pulse on write FF100004. If we wanted to build an input-output register acted like a general purpose read-write storate location, we would wire all of the flipflops making up that register as we have done with the interrupt-enable bit.
The error flipflop is the most complex of the three flipflops making up the keyboard status register. This is a positive-edge-triggered D flipflop that is clocked by the keypress input from the keyboard, and takes its data from the input ready bit. Because the positive on keypress also sets the ready bit, you might think that these two flipflops might hold the same thing. The key thing to note here is that the error flipflop is positive edge triggered, so it samples the ready bit just as the keypress pulse begins. As a result, the error bit is set if the ready bit was already set when someone pressed another key on the keyboard.
Exercises
h) How does the error flipflop in the keyboard interface get reset?
i) When you do a write to FF100004, what happens to bits 0 to 6 and 8 to 31 of the data written to memory? Answer with reference to the device register design given here!
j) When you do a read from FF100004, what value do you expect in bits 1 to 5 and 8 to 31 of the data read from memory? 0 to 6 and 8 to 31 of the data written to memory? Answer with reference to the device register design given here!
As mentioned at the start of this chapter, the Hawk display output device is very different from the keyboard input. The default display is memory-mapped, using a display controller that constantly scans a region of memory called the video RAM in order to create the display you see on your screen.
In the case of the instructional emulator for the Hawk, this video RAM holds a rectangular array of characters, and we have assumed that there is hardware to translate these characters to an array of pixels on a display screen. This is comparable to the original IBM PC Monochrome Display Adapter from 1981. This is used here primarily because more complex graphics display technology requires more complex system software to perform even the simplest of graphics display functions. The basic idea of memory mapped display hardware, however, stays the same whether the hardware generates text from the display or just displays pixels.
Simple display interfaces for the Hawk occupy memory locations from FF00000016 potentially all the way up to FF0FFFFF16. The first two words of the display interface give the number of lines on the display and the number of columns. For text displays, the default, lines and columns are measured in characters, so the default text display might be 24 lines of 80 characters each. When running the Hawk emulator, these are set automatically to the size of the text window being used by the emulator, minus the size of the part of the window used for displaying the registers and memory. In real hardware, it might be necessary to set lines and columns to match the resolution of the physical video monitor being used.
The actual video RAM for the Hawk begins at location FF00010016 and consists of lines × columns consecutive bytes of memory, starting at the upper lefthand corner of the screen. Each byte of the video RAM holds one character of text, encoded in ASCII, but simple graphics displays with one byte per pixel would operate similarly.
| FF000000 |
| ||
| FF000004 |
| ||
| FF000008 |
| ||
| FF0000FC | |||
| FF000100 |
| ||
| lines consecutive blocks | |||
| of columns bytes each | |||
Given this, the following simple function displays displaying one character at a given row and column of the screen:
void dispcharat( char ch, unsigned int col, unsigned int line )
{
const unsigned int * plines = 0xFF000000;
const unsigned int * pcolumns = 0xFF000004;
const char * origin = 0xFF000100;
if ( (col < (* pcolumns)) && (line < (* plines)) ) {
* (origin + line * (* pcolumns) + col ) = ch;
}
}
|
This code shows one character at the given location, after checking for coordinates outside the display area. This is not a convenient way to use the display! Most text is displayed in consecutive locations, so it is annoying for the user to be saddled with the job of giving coordinates for each character. Not only that, but this code does a multiply for each character displayed, an unnecessary expense if most characters are displayed consecutively.
We can fix these problems by dividing the function of setting the display coordinates from that of displaying text. The Hawk monitor does this using dspat() to set display coordinates, and dspch() to display text. These communicate through a COMMON block that holds the current address in video RAM. dspat() sets this address, while dspch() stores a character there and increments the address. In C, we could describe this as follows:
static unsigned int * plines = 0xFF000000;
static unsigned int * pcolumns = 0xFF000004;
static char * origin = 0xFF000100;
static char * dspptr = origin;
void dspat( unsigned int col, unsigned int line )
{
dspptr = origin + line * (* pcolumns) + col;
}
void dspch( char ch )
{
* dspptr = ch;
dspptr = dspptr + 1;
}
|
In reading the above code, recall that, in C, the type int* means pointer to integer, and so the declaration int* pcolumns means that plines is a pointer to, or the address of, an integer variable, and *pcolumns is this variable. In this code, plines, pcolumns and origin should be declared as constants, but that would require discussion of even more obscure features of C and C++.
In the above code, dspptr, the pointer to the next character to be displayed, is set not only by dspat() but also by an initializer. In the Hawk assembly language version of this code, we use the DSPINI routine to do this and to return, to the user, the dimensions of the display screen. The following code sufficies for this:
COMMON DSPPTR,4 ; address of current display position PDSPPTR:W DSPPTR PDSP: W #FF000000 ; base address of display interface ; the following fields exist within the display interface LINES = #0 ; number of lines on screen COLUMNS = #4 ; number of columns per line ORIGIN = #100 ; row 0 column 0 of display data INT DSPINI ; initialize the display DSPINI: ; link through R1 ; returns R3 = columns (screen width) ; R4 = lines (screen height) ; does not use any other registers LOAD R3,PDSP LEA R3,R3,ORIGIN ; /* compute address of origin field */ LOAD R4,PDSPPTR STORES R3,R4 ; dspptr = &(pdsp->origin) LOAD R4,PDSP LOAD R3,R4,COLUMNS ; R3 = pdsp->columns LOAD R4,R4,LINES ; R4 = pdsp->lines JUMPS R1 ; return |
Exercises
k) What happens if a user of the dspch() routine given above displays more consecutive characters than will fit on a line?
l) Modify the dspat() routine given above so that it will not set the display pointer the bounds of the video RAM defined by the number of lines and columns on the screen. Attempts to set coordinates outside the screen should set the coordinate to the nearest on-screen location to the coordinate given by the user.
m) Write a version of DSPCH that is consistant with the version of DSPINI given here.
n) Write a version of DSPAT that is consistant with the version of DSPINI given here.
It is fair to ask, how much more complex is text output when the video RAM holds one pixel in each byte instead of one character? The answer is, considerably, but we can hide this complexity if we write a few key routines. The most important of these is the "pixel block transfer" routine, still frequently known as bitblit because it was originally developed for systems that had one bit per pixel, back in the 1970's. This routine copies a rectangular block of pixels from a region of one 2-dimensional array of pixels to a region of the destination array of pixels.
The source and destination arrays for the bitblit operation are described by their starting addresses, the number of rows of pixels in the array, and the number of columns of pixels in the array. The location in each array holding the block of pixels to be addressed is described by the row and column number of the upper left corner, and the size of the region to copy is described by a height and width. Adding these up, it is easy to see that the bitblit operator takes a total of 12 parameters!
Given a working bitblit operator and a pixel array holding the current font, plus a table giving the location, height and width of each letter in the alphabet, displaying one letter on the screen requires a single call to bitblit to copy that letter into place, plus an add to update the current display position by the width of that letter.
One byte per pixel allows for an impressive monochrome display, but for color, we really need at least 18 bits per pixel, 6 bits each for reg, green and blue. Because most modern computers have 8 bit bytes and 32-bit words, it is common to use either 24 bits per pixel or 32 bits per pixel. In the latter case, the extra 8 bits per pixel are sometimes used to indicate the transparency of the pixel, so that when the bitblit operator merges one pixel with another, it can combine them according to their relative transparencies instead of simply replacing one with another.
The performance of the bitblit operator is the key to fast graphics! Because of this, and the complexity of the underlying computation, major efforts have been put into developing fast implementations of this. All of the optimization techniques discussed in the context of the strlen function in Chapter 7 have been applied to this operator, so that, when pixels are one-bit or 8-bits each, they can be copied in one word blocks whenever possible. In addition, the central service offered by many graphics coprocessors is a fast version of bitblit, frequently augmented with additional transformations such as the ability to dim, blurr, rescale or distort a block of pixels as it is copied.
Exercises
o) Write out the full parameter list for bitblit().
p) Describe how the bitblit() operator can be used to scroll a text window up one line, in order to make room for a new line of text at the bottom of the screen.
The actual hardware of a video display interface is quite a bit more complex than the simple keyboard interface we described previously. To understand why this must be so, we need to look briefly at the nature of video data.
A video data stream consists of a sequence of images, repeated many times per second. For classical broadcast television in the United States, the refresh rate is 60 half-frames per second. Video frames are separated by interframe gaps, called vertical blanking intervals. Each frame is transmitted as a sequence of lines; standard broadcast television uses 261 lines per half-frame. Just as frames are separated by interframe gaps, lines within a frame are separated by interline gaps, called horizontal blanking intervals. Within each line, the sequence of brightness values to be displayed are conveyed as analog voltages. During the blanking intervals, a special voltage called ultrablack is transmitted in order to synchronize the display.
The use of half-frames in classical broadcast video is because the frames are interlaced. The display resolution, taking interlacing into account, is 522 lines per full-frame, with 30 full frames per second. The basic refresh rate, 60 half-frames per second, was chosen because alternating current is distributed in the United States at 60 Hertz, or cycles per second. We will ignore interlaced video and half frames here, but we will assume that the video interface must deal with the remaining details.
The complexity of a video signal, with horizontal and vertical blanking intervals interrupting the repeated scan of a 2-dimensional array of pixels, is sufficient that video output is always generated by a special processor that includes registers for counting pixels on a line and lines on the display. This processor has access to main memory, or at least to that part of main memory used for video RAM, so we refer to it as having direct memory access.
Just as we describe the function of a central processing unit by the algorithm it carries out, the fetch-execute cycle, we can also describe a special purpose processor such as the video display controller in terms of the algorithm it carries out. Here is the algorithm a simple video controller might use to generate video output assuming that pixels are one byte each:
unsigned int lines; /* controller interface registers */
unsigned int columns;
char * origin;
video_controller() {
unsigned int line;
unsigned int column;
char * addr;
while (TRUE) do { /* display frames forever */
addr = origin;
output( ultrablack );
wait( vertical_blanking_interval );
for (line = 0; line < lines; line++) {
output( ultrablack );
wait( horizontal_blanking_interval );
for (column = 0; column < columns; column++) {
output( * addr );
wait( pixel_duration );
addr = addr + 1;
}
}
}
}
|
Video controllers for text-only displays are somewhat more complex; typically, these include a read-only memory holding the pixel patterns for the characters. If each character is stored as an 8 by 16 array of pixels, with one bit per pixel, each line of text must be scanned 16 times in order to generate 16 rows of pixels, and for each row of each character in the line, the 8 pixels of that row must be output, one pixel at a time, to the video stream.
Prior to 1970, the hardware to do this was very expensive, and few but the most expensive computers had graphics output displays. The most common output device was the impact printer, either high-speed line printers or low-speed teleprinters, typically operating at 10 characters per second and using 110 baud serial communication links.
By 1973, small solid-state memories were available that could hold one screenful of text, and video displays became common. These were text-only displays because the extra logic needed in the controller for text-only display was less expensive than the many kilobytes of memory needed for a graphical display. It was only in the 1980's that memory became inexpensive enough that graphics displays became commonplace.
Exercises
q) Write code in the style of code given here for a pixel mapped video display controller to describe the algorithm executed by the hardware of one of the older but more complex text-only video displays.
r) Write code in the style of code given here for a pixel mapped video display controller to describe the algorithm executed by the hardware of a display controller that produces interlaced half-frames. This should scan every-other line of the video RAM for each half-frame, starting the first line of even half-frames in mid-line. The short first line of even half-frames is how the receiver knows to interlace the lines!