
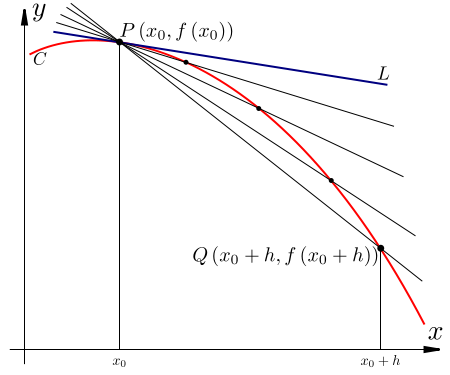
That is $$\text{slope of the tangent line =} f{~\prime(p)} = lim_{h \rightarrow 0} \frac{f(p+h) - f(p)}{p+h - p}$$


If $(x, y)$ is a point on the tangent line to $y = f(x)$ at the point $(p, f(p))$, then we can find the equation of the tangent line from $$f{~\prime(p)} = \frac{y - f(p)}{x - p}$$ images from http://math4allages.files.wordpress.com/2009/12/introlimits4.png, http://upload.wikimedia.org/wikipedia/commons/thumb/2/24/Tangent_as_Secant_Limit.svg/450px-Tangent_as_Secant_Limit.svg.png