If $y = f(x)$ is a differentiable function, then
$f{~\prime(p)}$ = the slope of the tangent line to $y = f(x)$ at the point $(p, f(p))$.

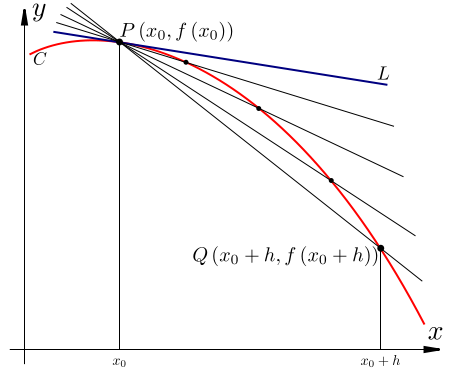
That is $$\text{slope of the tangent line =} f{~\prime(p)} = lim_{h \rightarrow 0} \frac{f(p+h) - f(p)}{p+h - p}$$

         

We can easily determine the equation of the tangent line to $y = f(x)$ at the point $(p, f(p))$: $y = mx + b$ where $m = f~\prime(p)$ and $b = $

If $(x, y)$ is a point on the tangent line to $y = f(x)$ at the point $(p, f(p))$, then we can find the equation of the tangent line from $$f{~\prime(p)} = \frac{y - f(p)}{x - p}$$