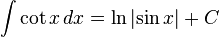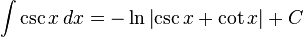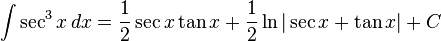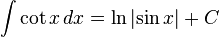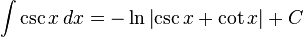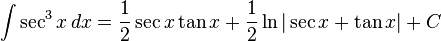$\frac{d(uv)}{dx} = u\frac{dv}{dx} + \frac{du}{dx} v $

$\int \frac{d(uv)}{dx}dx = \int u\frac{dv}{dx}dx + \int \frac{du}{dx} v dx $

$uv = \int u{dv} + \int v {du} $

Integration by parts: $\int u{dv} = uv - \int v du$

Formulus below copied from wikipedia:

Exponential functions

\int a^x\,dx = \frac{a^x}{\ln a} + C

Logarithms

\int \ln x\,dx = x \ln x - x + C
\int \log_a x\,dx = x\log_a x - \frac{x}{\ln a} + C

[edit] Trigonometric functions

more integrals: List of integrals of trigonometric functions
\int \sin{x}\, dx = -\cos{x} + C
\int \cos{x}\, dx = \sin{x} + C
\int \tan{x} \, dx = -\ln{\left| \cos {x} \right|} + C = \ln{\left| \sec{x} \right|} + C
\int \cot{x} \, dx = \ln{\left| \sin{x} \right|} + C
\int \sec{x} \, dx = \ln{\left| \sec{x} + \tan{x}\right|} + C
\int \csc{x} \, dx = -\ln{\left| \csc{x} + \cot{x}\right|} + C
\int \sec^2 x \, dx = \tan x + C
\int \csc^2 x \, dx = -\cot x + C
\int \sec{x} \, \tan{x} \, dx = \sec{x} + C
\int \csc{x} \, \cot{x} \, dx = -\csc{x} + C
\int \sin^2 x \, dx = \frac{1}{2}\left(x - \frac{\sin 2x}{2} \right) + C = \frac{1}{2}(x - \sin x\cos x ) + C
\int \cos^2 x \, dx = \frac{1}{2}\left(x + \frac{\sin 2x}{2} \right) + C = \frac{1}{2}(x + \sin x\cos x ) + C
\int \sec^3 x \, dx = \frac{1}{2}\sec x \tan x + \frac{1}{2}\ln|\sec x + \tan x| + C